Número de Fibonacci

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Integer en la secuencia infinita de Fibonacci

Un revestimiento con cuadrados cuyas longitudes laterales son números de Fibonacci sucesivos: 1, 2, 3, 5, 8, 13 y 21.

En matemáticas, los números de Fibonacci, comúnmente denominados $F n$ , forman una secuencia, la secuencia de Fibonacci, en la que cada número es la suma de los dos anteriores. La secuencia comúnmente comienza desde 0 y 1, aunque algunos autores comienzan la secuencia desde 1 y 1 o, a veces (como Fibonacci) desde 1 y 2. A partir de 0 y 1, los primeros valores de la secuencia son:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.

Los números de Fibonacci se describieron por primera vez en las matemáticas indias, ya en el año 200 a. C. en el trabajo de Pingala sobre la enumeración de posibles patrones de poesía sánscrita formada a partir de sílabas de dos longitudes. Llevan el nombre del matemático italiano Leonardo de Pisa, más tarde conocido como Fibonacci, quien introdujo la secuencia en las matemáticas de Europa occidental en su libro de 1202 Liber Abaci.

Los números de Fibonacci aparecen inesperadamente a menudo en matemáticas, tanto que hay una revista completa dedicada a su estudio, el Fibonacci Quarterly. Las aplicaciones de los números de Fibonacci incluyen algoritmos informáticos como la técnica de búsqueda de Fibonacci y la estructura de datos del montón de Fibonacci, y gráficos llamados cubos de Fibonacci que se utilizan para interconectar sistemas paralelos y distribuidos. También aparecen en entornos biológicos, como la ramificación de los árboles, la disposición de las hojas en un tallo, los brotes de la fruta de una piña, la floración de una alcachofa, un helecho que se despliega y la disposición de las brácteas de un cono de pino..

Los números de Fibonacci también están fuertemente relacionados con la proporción áurea: la fórmula de Binet expresa el $n$ ésimo número de Fibonacci en términos de $n$ y la proporción áurea, e implica que la proporción de dos números de Fibonacci consecutivos tiende a la proporción áurea como $n$ aumenta. Los números de Fibonacci también están estrechamente relacionados con los números de Lucas, que obedecen a la misma relación de recurrencia y con los números de Fibonacci forman un par complementario de secuencias de Lucas.

Definición

La espiral Fibonacci: una aproximación de la espiral dorada creada por arcos circulares de dibujo que conectan los rincones opuestos de los cuadrados en el revestimiento Fibonacci; (ver imagen anterior)

Los números de Fibonacci pueden definirse por la relación de recurrencia

{displaystyle F_{0}=0,quad F_{1}=1,}

{displaystyle F_{n}=F_{n-1}+F_{n-2}}

n ■ 1

Bajo algunas definiciones anteriores, el valor $F_{0}=0$ es omitido, así que la secuencia comienza con ${displaystyle F_{1}=F_{2}=1,}$ y la recurrencia ${displaystyle F_{n}=F_{n-1}+F_{n-2}}$ es válido para $n ■ 2$ .

Los primeros 20 números de Fibonacci $F n$ son:

F₀	F₁	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F₉	F₁₀	F₁₁	F₁₂	F₁₃	F₁₄	F₁₅	F₁₆	F₁₇	F₁₈	F₁₉
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181

Historia

13 añosF₇) maneras de arreglar sílabas largas y cortas en una cadencia de la longitud seis. OchoF₆) terminan con una sílaba corta y cinco (F₅Termina con una larga sílaba.

La sucesión de Fibonacci aparece en las matemáticas indias, en relación con la prosodia sánscrita. En la tradición poética sánscrita, había interés en enumerar todos los patrones de sílabas largas (L) de 2 unidades de duración, yuxtapuestas con sílabas cortas (S) de 1 unidad de duración. Contar los diferentes patrones de L y S sucesivas con una duración total determinada da como resultado los números de Fibonacci: el número de patrones de duración $m$ unidades es $F m + 1$ .

El conocimiento de la secuencia de Fibonacci se expresó ya en Pingala (c. 450 BC–200 BC). Singh cita la fórmula críptica de Pingala misrau cha ("los dos están mezclados") y los académicos que la interpretan en contexto diciendo que la cantidad de patrones para $m$ latidos ( $F m +1$ ) se obtiene sumando una [S] a la $F m$ casos y uno [L] a los casos $F m -1$ . Bharata Muni también expresa conocimiento de la secuencia en el Natya Shastra (c. 100 a. C.–c. 350 d. C.). Sin embargo, la exposición más clara de la secuencia surge en el trabajo de Virahanka (c. 700 d. C.), cuyo propio trabajo se ha perdido, pero está disponible en una cita de Gopala (c. 1135):

Variaciones de dos metros anteriores [es la variación]... Por ejemplo, para [un metro de longitud] cuatro, variaciones de metros de dos [y] tres mezclados, cinco ocurren. [trabaja ejemplos 8, 13, 21]... De esta manera, el proceso debe ser seguido en todos mātrā-v erttas [combinaciones prosódicas].

A Hemachandra (c. 1150) también se le atribuye el conocimiento de la secuencia, y escribe que "la suma del último y el anterior al último es el número... del siguiente mātrā-vṛtta.& #34;

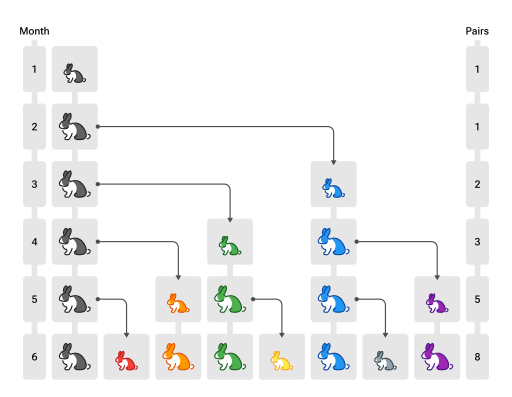
Fuera de la India, la sucesión de Fibonacci aparece por primera vez en el libro Liber Abaci (El libro del cálculo, 1202) de Fibonacci, donde se utiliza para calcular el crecimiento del conejo. poblaciones Fibonacci considera el crecimiento de una población de conejos idealizada (biológicamente poco realista), asumiendo que: una pareja de conejos reproductores recién nacidos se colocan en un campo; cada pareja reproductora se aparea a la edad de un mes, y al final de su segundo mes siempre producen otra pareja de conejos; y los conejos nunca mueren, sino que continúan reproduciéndose para siempre. Fibonacci planteó el rompecabezas: ¿cuántas parejas habrá en un año?

Al final del primer mes, se aparejan, pero todavía hay sólo 1 par.
Al final del segundo mes producen un nuevo par, por lo que hay 2 pares en el campo.

Una página de Fibonacci Liber Abaci de la Biblioteca Nazionale di Firenze mostrando (en caja a la derecha) 13 entradas de la secuencia Fibonacci:
los índices de presente a XII (meses) como ordinal latino y numerales romanos y los números (de pares de conejos) como números hindú-árabe comenzando con 1, 2, 3, 5 y terminando con 377.
Al final del tercer mes, el par original produce un segundo par, pero el segundo solo se mate para gestar durante un mes, por lo que hay 3 pares en todos.
Al final del cuarto mes, el par original ha producido otro par nuevo, y el par nacido hace dos meses también produce su primer par, haciendo 5 pares.

Al final del $n$ mes, el número de parejas de conejos es igual al número de parejas adultas (es decir, el número de parejas en el mes $n - 2$ ) más el número de parejas vivas el mes pasado (mes $n - 1$ ). El número en el $n$ ésimo mes es el $n$ ésimo Fibonacci número.

En una creciente población idealizada, el número de parejas de conejos forman la secuencia Fibonacci. At el final de la na mes, el número de pares es igual a F_No.

El nombre "secuencia de Fibonacci" fue utilizado por primera vez por el teórico de números del siglo XIX Édouard Lucas.

Relación con la proporción áurea

Expresión de forma cerrada

Como toda secuencia definida por una recurrencia lineal con coeficientes constantes, los números de Fibonacci tienen una expresión de forma cerrada. Se ha dado a conocer como la fórmula de Binet, en honor al matemático francés Jacques Philippe Marie Binet, aunque ya la conocían Abraham de Moivre y Daniel Bernoulli:

{displaystyle F_{n}={frac {varphi ^{n}-psi ^{n}}{varphi -psi }}={frac {varphi ^{n}-psi ^{n}}{sqrt {5}}},}

{displaystyle varphi ={frac {1+{sqrt {5}}}{2}}approx 1.61803,39887ldots }

↑

{displaystyle psi ={frac {1-{sqrt {5}}}{2}}=1-varphi =-{1 over varphi }approx -0.61803,39887ldots.}

Desde ${displaystyle psi =-varphi ^{-1}}$ , esta fórmula también se puede escribir como

{displaystyle F_{n}={frac {varphi ^{n}-(-varphi)^{-n}}{sqrt {5}}}={frac {varphi ^{n}-(-varphi)^{-n}}{2varphi -1}}.}

Para ver la relación entre la secuencia y estas constantes, observe que $φ$ y $ψ$ son ambas soluciones de la ecuación

{displaystyle x^{2}=x+1quad {text{and, thus,}}quad x^{n}=x^{n-1}+x^{n-2},}

φ

↑

{displaystyle varphi ^{n}=varphi ^{n-1}+varphi ^{n-2}}

{displaystyle psi ^{n}=psi ^{n-1}+psi ^{n-2}.}

Se deduce que para cualquier valor $a$ y $b$ , la secuencia definida por

{displaystyle U_{n}=avarphi ^{n}+bpsi ^{n}}

{displaystyle U_{n}=avarphi ^{n}+bpsi ^{n}=a(varphi ^{n-1}+varphi ^{n-2})+b(psi ^{n-1}+psi ^{n-2})=avarphi ^{n-1}+bpsi ^{n-1}+avarphi ^{n-2}+bpsi ^{n-2}=U_{n-1}+U_{n-2}}

Si se eligen $a$ y $b$ de modo que U₀ = 0 y $U 1 = 1$ entonces la secuencia resultante $U n$ debe Sea la sucesión de Fibonacci. Esto es lo mismo que requerir que $a$ y $b$ satisfagan el sistema de ecuaciones:

{displaystyle left{{begin{array}{l}a+b=0\varphi a+psi b=1end{array}}right.}

{displaystyle a={frac {1}{varphi -psi }}={frac {1}{sqrt {5}}},quad b=-a,}

Tomando los valores iniciales $U 0$ y $U 1$ constantes arbitrarias, una solución más general es:

{displaystyle U_{n}=avarphi ^{n}+bpsi ^{n}}

{displaystyle a={frac {U_{1}-U_{0}psi }{sqrt {5}}}}

{displaystyle b={frac {U_{0}varphi -U_{1}}{sqrt {5}}}.}

Cálculo por redondeo

Desde

<math alttext="{displaystyle left|{frac {psi ^{n}}{sqrt {5}}}right|Silencio↑ ↑ n5Silencio.12{displaystyle lefttención{frac {fn} {fn} {fn}}}justo de la vida {1}{2}}}<img alt="{displaystyle left|{frac {psi ^{n}}{sqrt {5}}}right|

para todos $n \geq 0$ , el número $F n$ es el entero más cercano a ${frac {varphi ^{n}}{sqrt {5}}}$ . Por lo tanto, se puede encontrar redondeando, utilizando la función de entero más cercana:

{displaystyle F_{n}=leftlfloor {frac {varphi ^{n}}{sqrt {5}}}rightrceil ngeq 0.}

De hecho, el error de redondeo es muy pequeño, siendo menor de 0,1 para $n \geq 4$ , y menor de 0,01 para $n \geq 8$ .

Los números de Fibonacci también se pueden calcular mediante truncamiento, en términos de la función de suelo:

{displaystyle F_{n}=leftlfloor {frac {varphi ^{n}}{sqrt {5}}}+{frac {1}{2}}rightrfloor ngeq 0.}

Como la función de piso es monótona, la última fórmula se puede invertir para encontrar el índice $n (F)$ del número de Fibonacci más pequeño que no sea menor que un entero positivo $F$ :

{displaystyle n(F)=leftlceil log _{varphi }left(Fcdot {sqrt {5}}-{frac {1}{2}}right)rightrceil}

{displaystyle log _{varphi }(x)=ln(x)/ln(varphi)=log _{10}(x)/log _{10}(varphi)}

{displaystyle ln(varphi)=0.481211ldots }

{displaystyle log _{10}(varphi)=0.208987ldots }

Magnitud

Desde F_n es asintotico a $varphi ^{n}/{sqrt {5}}$ , el número de dígitos en F_n es asintotico a ${displaystyle nlog _{10}varphi approx 0.2090,n}$ . Como consecuencia, por cada entero d 1 hay 4 o 5 números de Fibonacci con d dígitos decimales.

Más generalmente, en la base b representación, el número de dígitos en F_n es asintotico a ${displaystyle nlog _{b}varphi.}$

Límite de cocientes consecutivos

Johannes Kepler observó que la proporción de números Fibonacci consecutivos converge. Él escribió que "como 5 es a 8 así es 8 a 13, prácticamente, y como 8 es a 13, así es 13 a 21 casi", y concluyó que estas ratios se acercan a la relación de oro ${displaystyle varphi colon }$

{displaystyle lim _{nto infty }{frac {F_{n+1}}{F_{n}}}=varphi.}

Esta convergencia tiene independientemente de los valores iniciales $U_{0}$ y $U_{1}$ , a menos que ${displaystyle U_{1}=-U_{0}/varphi }$ . Esto se puede verificar usando la fórmula de Binet. Por ejemplo, los valores iniciales 3 y 2 generan la secuencia 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555,... La proporción de términos consecutivos en esta secuencia muestra la misma convergencia hacia la relación dorada.

En general, ${displaystyle lim _{nto infty }{frac {F_{n+m}}{F_{n}}}=varphi ^{m}}$ , porque las relaciones entre los números de Fibonacci consecutivos se aproximan $varphi$ .

Tilings exitosos del plano y un gráfico de aproximaciones a la relación dorada calculada dividiendo cada número Fibonacci por el anterior

Descomposición de potencias

Dado que la proporción áurea satisface la ecuación

{displaystyle varphi ^{2}=varphi +1,}

esta expresión se puede utilizar para descomponer poderes superiores $varphi ^{n}$ como una función lineal de potencias inferiores, que a su vez se puede descomponer todo el camino hasta una combinación lineal de $varphi$ y 1. Las relaciones de recurrencia resultantes dan a los números Fibonacci como coeficientes lineales:

{displaystyle varphi ^{n}=F_{n}varphi +F_{n-1}.}

n ≥ 1

{displaystyle varphi ^{n+1}=(F_{n}varphi +F_{n-1})varphi =F_{n}varphi ^{2}+F_{n-1}varphi =F_{n}(varphi +1)+F_{n-1}varphi =(F_{n}+F_{n-1})varphi +F_{n}=F_{n+1}varphi +F_{n}.}

{displaystyle psi =-1/varphi }

{displaystyle psi ^{2}=psi +1}

{displaystyle psi ^{n}=F_{n}psi +F_{n-1}.}

Estas expresiones también son verdaderas para n 1 si la secuencia de Fibonacci F_n se extiende a los enteros negativos usando la regla Fibonacci ${displaystyle F_{n}=F_{n+2}-F_{n+1}.}$

Identificación

La fórmula de Binet proporciona una prueba de que un entero positivo x es un número de Fibonacci si y sólo si al menos uno de $5x^{2}+4$ o $5x^{2}-4$ es un cuadrado perfecto. Esto es porque la fórmula de Binet, que se puede escribir como ${displaystyle F_{n}=(varphi ^{n}-(-1)^{n}varphi ^{-n})/{sqrt {5}}}$ , puede ser multiplicado por ${displaystyle {sqrt {5}}varphi ^{n}}$ y resuelto como una ecuación cuadrática en $varphi ^{n}$ a través de la fórmula cuadrática:

{displaystyle varphi ^{n}={frac {F_{n}{sqrt {5}}pm {sqrt {5{F_{n}}^{2}+4(-1)^{n}}}}{2}}.}

Comparando esto ${displaystyle varphi ^{n}=F_{n}varphi +F_{n-1}=(F_{n}{sqrt {5}}+F_{n}+2F_{n-1})/2}$ , sigue que

{displaystyle 5{F_{n}}^{2}+4(-1)^{n}=(F_{n}+2F_{n-1})^{2},.}

En particular, el lado izquierdo es un cuadrado perfecto.

Forma matricial

Un sistema bidimensional de ecuaciones en diferencias lineales que describe la sucesión de Fibonacci es

{displaystyle {F_{k+2} choose F_{k+1}}={begin{pmatrix}1&1\1&0end{pmatrix}}{F_{k+1} choose F_{k}}}

{displaystyle {vec {F}}_{k+1}=mathbf {A} {vec {F}}_{k},}

que rinde ${vec {F}}_{n}=mathbf {A} ^{n}{vec {F}}_{0}$ . Los valores de la matriz $A$ son ${displaystyle varphi ={frac {1}{2}}(1+{sqrt {5}})}$ y ${displaystyle psi =-varphi ^{-1}={frac {1}{2}}(1-{sqrt {5}})}$ correspondiente a los respectivos eigenvectores

{displaystyle {vec {mu }}={varphi choose 1}}

{displaystyle {vec {nu }}={-varphi ^{-1} choose 1}.}

{displaystyle {vec {F}}_{0}={1 choose 0}={frac {1}{sqrt {5}}}{vec {mu }}-{frac {1}{sqrt {5}}}{vec {nu }},}

n

{displaystyle {begin{aligned}{vec {F}}_{n}&={frac {1}{sqrt {5}}}A^{n}{vec {mu }}-{frac {1}{sqrt {5}}}A^{n}{vec {nu }}\&={frac {1}{sqrt {5}}}varphi ^{n}{vec {mu }}-{frac {1}{sqrt {5}}}(-varphi)^{-n}{vec {nu }}~\&={cfrac {1}{sqrt {5}}}left({cfrac {1+{sqrt {5}}}{2}}right)^{n}{varphi choose 1}-{cfrac {1}{sqrt {5}}}left({cfrac {1-{sqrt {5}}}{2}}right)^{n}{-varphi ^{-1} choose 1},end{aligned}}}

n

{displaystyle F_{n}={cfrac {1}{sqrt {5}}}left({cfrac {1+{sqrt {5}}}{2}}right)^{n}-{cfrac {1}{sqrt {5}}}left({cfrac {1-{sqrt {5}}}{2}}right)^{n}.}

De manera equivalente, el mismo cálculo puede realizarse mediante la diagonalización de $A$ mediante el uso de su descomposición propia:

{displaystyle {begin{aligned}A&=SLambda S^{-1},\A^{n}&=SLambda ^{n}S^{-1},end{aligned}}}

Lambda ={begin{pmatrix}varphi &0\0&-varphi ^{-1}end{pmatrix}}

{displaystyle S={begin{pmatrix}varphi &-varphi ^{-1}\1&1end{pmatrix}}.}

n

{displaystyle {begin{aligned}{F_{n+1} choose F_{n}}&=A^{n}{F_{1} choose F_{0}}\&=SLambda ^{n}S^{-1}{F_{1} choose F_{0}}\&=S{begin{pmatrix}varphi ^{n}&0\0&(-varphi)^{-n}end{pmatrix}}S^{-1}{F_{1} choose F_{0}}\&={begin{pmatrix}varphi &-varphi ^{-1}\1&1end{pmatrix}}{begin{pmatrix}varphi ^{n}&0\0&(-varphi)^{-n}end{pmatrix}}{frac {1}{sqrt {5}}}{begin{pmatrix}1&varphi ^{-1}\-1&varphi end{pmatrix}}{1 choose 0},end{aligned}}}

que de nuevo produce

{displaystyle F_{n}={cfrac {varphi ^{n}-(-varphi)^{-n}}{sqrt {5}}}.}

La matriz $A$ tiene un determinante de −1 y, por lo tanto, es una matriz unimodular de 2×2.

Esta propiedad se puede entender en términos de la representación de fracción continua para la proporción áurea:

{displaystyle varphi =1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}.}

Los números de Fibonacci se presentan como la razón de convergentes sucesivos de la fracción continua para $φ$ , y la matriz formada por convergentes sucesivos de cualquier fracción continua tiene un determinante de +1 o −1. La representación matricial da la siguiente expresión de forma cerrada para los números de Fibonacci:

{displaystyle {begin{pmatrix}1&1\1&0end{pmatrix}}^{n}={begin{pmatrix}F_{n+1}&F_{n}\F_{n}&F_{n-1}end{pmatrix}}.}

Para un $n$ dado, esta matriz se puede calcular en $O (log(n))$ operaciones aritméticas, usando el método de exponenciación por cuadrado.

Tomando el determinante de ambos lados de esta ecuación se obtiene la identidad de Cassini,

{displaystyle (-1)^{n}=F_{n+1}F_{n-1}-{F_{n}}^{2}.}

Además, desde $A n A m = A n + m$ para cualquier cuadrado matriz $A$ , se pueden derivar las siguientes identidades (se obtienen a partir de dos coeficientes diferentes del producto matricial, y uno puede deducir fácilmente el segundo de el primero cambiando $n$ por $n + 1$ ),

{displaystyle {begin{aligned}{F_{m}}{F_{n}}+{F_{m-1}}{F_{n-1}}&=F_{m+n-1},\F_{m}F_{n+1}+F_{m-1}F_{n}&=F_{m+n}.end{aligned}}}

En particular, con $m = n$ ,

{displaystyle {begin{array}{ll}F_{2n-1}&={F_{n}}^{2}+{F_{n-1}}^{2}\F_{2n}&=(F_{n-1}+F_{n+1})F_{n}\&=(2F_{n-1}+F_{n})F_{n}\&=(2F_{n+1}-F_{n})F_{n}.end{array}}}

Estas dos últimas identidades proporcionan una forma de calcular números de Fibonacci recursivamente en $O (log(n))$ aritmética operaciones y en el tiempo $O (M (n) log(n))$ , donde $M (n)$ es el tiempo para la multiplicación de dos números de $n$ dígitos. Esto coincide con el tiempo para calcular el $n$ ésimo número de Fibonacci de la fórmula de matriz de forma cerrada, pero con menos pasos redundantes si se evita volver a calcular un número ya calculado. Número de Fibonacci (recursividad con memorización).

Identidades combinatorias

Pruebas combinatorias

La mayoría de las identidades que involucran números de Fibonacci pueden probarse utilizando argumentos combinatorios usando el hecho de que $F_{n}$ puede ser interpretado como el número de secuencias [posiblemente vacías] de 1s y 2s cuya suma es $n-1$ . Esto se puede tomar como la definición ${displaystyle F_{n}}$ con las convenciones ${displaystyle F_{0}=0}$ , que significa que no existe tal secuencia cuya suma es −1, y ${displaystyle F_{1}=1}$ , lo que significa la secuencia vacía "adds up" a 0. En lo siguiente, ${displaystyle |{...}|}$ es la cardinalidad de un conjunto:

{displaystyle F_{0}=0=|{}|}

{displaystyle F_{1}=1=|{{}}|}

{displaystyle F_{2}=1=|{{1}}|}

{displaystyle F_{3}=2=|{{1,1},{2}}|}

{displaystyle F_{4}=3=|{{1,1,1},{1,2},{2,1}}|}

{displaystyle F_{5}=5=|{{1,1,1,1},{1,1,2},{1,2,1},{2,1,1},{2,2}}|}

De esta manera la relación de recurrencia

{displaystyle F_{n}=F_{n-1}+F_{n-2}}

{displaystyle F_{n}}

{displaystyle F_{n}=|{{1,...},{1,...},...}|+|{{2,...},{2,...},...}|}

n-2

n-3

{displaystyle F_{n-1}}

{displaystyle F_{n-2}}

{displaystyle F_{n-1}+F_{n-2}}

{displaystyle F_{n}}

De manera similar, se puede demostrar que la suma de los primeros números de Fibonacci hasta el nésimo es igual al (n + 2)-segundo número de Fibonacci menos 1 En símbolos:

{displaystyle sum _{i=1}^{n}F_{i}=F_{n+2}-1}

Esto puede ser visto dividiendo todas las secuencias resumiendo a $n+1$ basado en la ubicación de la primera 2. Específicamente, cada conjunto consiste en las secuencias que comienzan ${displaystyle {2,...},{1,2,...},...,}$ hasta los dos últimos sets ${displaystyle {{1,1,...,1,2}},{{1,1,...,1}}}$ cada uno con cardenalidad 1.

Siguiendo la misma lógica que antes, sumando la cardinalidad de cada conjunto vemos que

{displaystyle F_{n+2}=F_{n}+F_{n-1}+...+|{{1,1,...,1,2}}|+|{{1,1,...,1}}|}

... donde los dos últimos términos tienen el valor ${displaystyle F_{1}=1}$ . De esto sigue que $sum _{{i=1}}^{n}F_{i}=F_{{n+2}}-1$ .

Un argumento similar, agrupar las sumas por la posición del primer 1 en lugar de los primeros 2 da dos identidades más:

{displaystyle sum _{i=0}^{n-1}F_{2i+1}=F_{2n}}

{displaystyle sum _{i=1}^{n}F_{2i}=F_{2n+1}-1.}

{displaystyle F_{2n-1}}

{displaystyle F_{2n}}

Se puede usar un truco diferente para probar

{displaystyle sum _{i=1}^{n}{F_{i}}^{2}=F_{n}F_{n+1}}

{displaystyle F_{n}}

{displaystyle F_{n}times F_{n+1}}

{displaystyle F_{n},F_{n-1},...,F_{1}}

Método simbólico

La secuencia ${displaystyle (F_{n})_{nin mathbb {N} }}$ también se considera utilizando el método simbólico. Más precisamente, esta secuencia corresponde a una clase combinatoria especificable. La especificación de esta secuencia es ${displaystyle operatorname {Seq} ({mathcal {Z+Z^{2}}})}$ . De hecho, como se ha indicado anteriormente, $n$ - el número Fibonacci es igual al número de composiciones combinatorias (particiones ordenadas) de $n-1$ usando los términos 1 y 2.

Se sigue que la función generadora ordinaria de la secuencia Fibonacci, es decir. ${displaystyle sum _{i=0}^{infty }F_{i}z^{i}}$ , es la función compleja ${displaystyle {frac {z}{1-z-z^{2}}}}$ .

Pruebas de inducción

Las identidades de Fibonacci a menudo se pueden demostrar fácilmente mediante inducción matemática.

Por ejemplo, reconsidere

{displaystyle sum _{i=1}^{n}F_{i}=F_{n+2}-1.}

{displaystyle F_{n+1}}

{displaystyle sum _{i=1}^{n}F_{i}+F_{n+1}=F_{n+1}+F_{n+2}-1}

y así tenemos la fórmula para $n+1$

{displaystyle sum _{i=1}^{n+1}F_{i}=F_{n+3}-1}

Análogamente, añadir ${displaystyle {F_{n+1}}^{2}}$ a ambos lados

{displaystyle sum _{i=1}^{n}{F_{i}}^{2}=F_{n}F_{n+1}}

{displaystyle sum _{i=1}^{n}{F_{i}}^{2}+{F_{n+1}}^{2}=F_{n+1}left(F_{n}+F_{n+1}right)}

{displaystyle sum _{i=1}^{n+1}{F_{i}}^{2}=F_{n+1}F_{n+2}}

Pruebas de la fórmula de Binet

La fórmula de Binet es

{displaystyle {sqrt {5}}F_{n}=varphi ^{n}-psi ^{n}.}

Por ejemplo, para probar que ${textstyle sum _{i=1}^{n}F_{i}=F_{n+2}-1}$ nota que el lado izquierdo multiplicado por ${displaystyle {sqrt {5}}}$ se convierte en

{displaystyle {begin{aligned}1+&varphi +varphi ^{2}+dots +varphi ^{n}-left(1+psi +psi ^{2}+dots +psi ^{n}right)\&={frac {varphi ^{n+1}-1}{varphi -1}}-{frac {psi ^{n+1}-1}{psi -1}}\&={frac {varphi ^{n+1}-1}{-psi }}-{frac {psi ^{n+1}-1}{-varphi }}\&={frac {-varphi ^{n+2}+varphi +psi ^{n+2}-psi }{varphi psi }}\&=varphi ^{n+2}-psi ^{n+2}-(varphi -psi)\&={sqrt {5}}(F_{n+2}-1)\end{aligned}}}

{textstyle varphi psi =-1}

{textstyle varphi -psi ={sqrt {5}}}

Otras identidades

Se pueden derivar muchas otras identidades usando varios métodos. Éstos son algunos de ellos:

Las identidades de Cassini y Catalan

La identidad de Cassini establece que

{displaystyle {F_{n}}^{2}-F_{n+1}F_{n-1}=(-1)^{n-1}}

{displaystyle {F_{n}}^{2}-F_{n+r}F_{n-r}=(-1)^{n-r}{F_{r}}^{2}}

Identidad de D''Ocagne N#39;

{displaystyle F_{m}F_{n+1}-F_{m+1}F_{n}=(-1)^{n}F_{m-n}}

{displaystyle F_{2n}={F_{n+1}}^{2}-{F_{n-1}}^{2}=F_{n}left(F_{n+1}+F_{n-1}right)=F_{n}L_{n}}

L_nn 'n

{displaystyle F_{3n}=2{F_{n}}^{3}+3F_{n}F_{n+1}F_{n-1}=5{F_{n}}^{3}+3(-1)^{n}F_{n}}

{displaystyle F_{3n+1}={F_{n+1}}^{3}+3F_{n+1}{F_{n}}^{2}-{F_{n}}^{3}}

{displaystyle F_{3n+2}={F_{n+1}}^{3}+3{F_{n+1}}^{2}F_{n}+{F_{n}}^{3}}

{displaystyle F_{4n}=4F_{n}F_{n+1}left({F_{n+1}}^{2}+2{F_{n}}^{2}right)-3{F_{n}}^{2}left({F_{n}}^{2}+2{F_{n+1}}^{2}right)}

De manera más general,

{displaystyle F_{kn+c}=sum _{i=0}^{k}{k choose i}F_{c-i}{F_{n}}^{i}{F_{n+1}}^{k-i}.}

o alternativamente

{displaystyle F_{kn+c}=sum _{i=0}^{k}{k choose i}F_{c+i}{F_{n}}^{i}{F_{n-1}}^{k-i}.}

Poniendo $k = 2$ en esta fórmula, se obtienen de nuevo las fórmulas del final de la sección anterior Forma de matriz.

Función generadora

La función generadora de la sucesión de Fibonacci es la serie de potencias

{displaystyle s(x)=sum _{k=0}^{infty }F_{k}x^{k}=sum _{k=1}^{infty }F_{k}x^{k}=0+x+x^{2}+2x^{3}+3x^{4}+dots.}

Esta serie es convergente para $<math alttext="{displaystyle |x|SilencioxSilencio.1φ φ ,{displaystyle Некиваниваный {frac}{varphi }}<img alt="|x|$ y su suma tiene una forma cerrada simple:

{displaystyle s(x)={frac {x}{1-x-x^{2}}}}

Esto se puede probar usando la recurrencia de Fibonacci para expandir cada coeficiente en la suma infinita:

{displaystyle {begin{aligned}s(x)&=sum _{k=0}^{infty }F_{k}x^{k}\&=F_{0}+F_{1}x+sum _{k=2}^{infty }F_{k}x^{k}\&=0+1x+sum _{k=2}^{infty }F_{k}x^{k}\&=x+sum _{k=2}^{infty }left(F_{k-1}+F_{k-2}right)x^{k}\&=x+sum _{k=2}^{infty }F_{k-1}x^{k}+sum _{k=2}^{infty }F_{k-2}x^{k}\&=x+xsum _{k=2}^{infty }F_{k-1}x^{k-1}+x^{2}sum _{k=2}^{infty }F_{k-2}x^{k-2}\&=x+xsum _{k=1}^{infty }F_{k}x^{k}+x^{2}sum _{k=0}^{infty }F_{k}x^{k}\&=x+xs(x)+x^{2}s(x).end{aligned}}}

Resolviendo la ecuación

{displaystyle s(x)=x+xs(x)+x^{2}s(x)}

La descomposición en fracciones parciales viene dada por

{displaystyle s(x)={frac {1}{sqrt {5}}}left({frac {1}{1-varphi x}}-{frac {1}{1-psi x}}right)}

varphi ={frac {1+{sqrt {5}}}{2}}

{displaystyle psi ={frac {1-{sqrt {5}}}{2}}}

${displaystyle -sleft(-{frac {1}{x}}right)}$ da la función generadora para los números negafibonacci, y $s(x)$ satisfice la ecuación funcional

{displaystyle s(x)=sleft(-{frac {1}{x}}right).}

Sumas recíprocas

Las sumas infinitas sobre números de Fibonacci recíprocos a veces se pueden evaluar en términos de funciones theta. Por ejemplo, la suma de todos los números de Fibonacci recíprocos indexados impares se puede escribir como

{displaystyle sum _{k=1}^{infty }{frac {1}{F_{2k-1}}}={frac {sqrt {5}}{4}};,vartheta _{2}!left(0,{frac {3-{sqrt {5}}}{2}}right)^{2},}

y la suma de los números de Fibonacci recíprocos al cuadrado como

{displaystyle sum _{k=1}^{infty }{frac {1}{{F_{k}}^{2}}}={frac {5}{24}}left(vartheta _{2}!left(0,{frac {3-{sqrt {5}}}{2}}right)^{4}-vartheta _{4}!left(0,{frac {3-{sqrt {5}}}{2}}right)^{4}+1right).}

Si sumamos 1 a cada número de Fibonacci en la primera suma, también existe la forma cerrada

{displaystyle sum _{k=1}^{infty }{frac {1}{1+F_{2k-1}}}={frac {sqrt {5}}{2}},}

y hay una suma anidada de números de Fibonacci al cuadrado que dan el recíproco de la proporción áurea,

{displaystyle sum _{k=1}^{infty }{frac {(-1)^{k+1}}{sum _{j=1}^{k}{F_{j}}^{2}}}={frac {{sqrt {5}}-1}{2}}.}

La suma de todos los números de Fibonacci recíprocos indexados pares es

{displaystyle sum _{k=1}^{infty }{frac {1}{F_{2k}}}={sqrt {5}}left(L{bigl (}psi ^{2}{bigr)}-L{bigl (}psi ^{4}{bigr)}right)}

{displaystyle textstyle L(q):=sum _{k=1}^{infty }{frac {q^{k}}{1-q^{k}}},}

{displaystyle textstyle {frac {1}{F_{2k}}}={sqrt {5}}left({frac {psi ^{2k}}{1-psi ^{2k}}}-{frac {psi ^{4k}}{1-psi ^{4k}}}right).}

Entonces, la constante de Fibonacci recíproca es

{displaystyle sum _{k=1}^{infty }{frac {1}{F_{k}}}=sum _{k=1}^{infty }{frac {1}{F_{2k-1}}}+sum _{k=1}^{infty }{frac {1}{F_{2k}}}=3.359885666243dots }

Además, Richard André-Jeannin ha demostrado que este número es irracional.

La serie de Millin da la identidad

{displaystyle sum _{k=0}^{infty }{frac {1}{F_{2^{k}}}}={frac {7-{sqrt {5}}}{2}},}

{displaystyle sum _{k=0}^{N}{frac {1}{F_{2^{k}}}}=3-{frac {F_{2^{N}-1}}{F_{2^{N}}}}.}

Primos y divisibilidad

Propiedades de divisibilidad

Cada tercer número de la secuencia es incluso (un múltiplo de ${displaystyle F_{3}=2}$ ) y, más generalmente, cada kt número de la secuencia es un múltiple de F_k. Así la secuencia de Fibonacci es un ejemplo de una secuencia de divisibilidad. De hecho, la secuencia Fibonacci satisface la propiedad más fuerte de la divisibilidad

{displaystyle gcd(F_{a},F_{b},F_{c},ldots)=F_{gcd(a,b,c,ldots)},}

gcd

En particular, los tres números consecutivos de Fibonacci son coprime pareados porque ambos $F_{1}=1$ y ${displaystyle F_{2}=1}$ . Eso es,

{displaystyle gcd(F_{n},F_{n+1})=gcd(F_{n},F_{n+2})=gcd(F_{n+1},F_{n+2})=1}

para cada n.

Todo número primo p divide un número de Fibonacci que se puede determinar por el valor de p módulo 5. Si p es congruente con 1 o 4 (mod 5), entonces p divide F_{p − 1}, y si p es congruente con 2 o 3 (mod 5), entonces, p divide F_{p + 1}. El caso restante es que p = 5, y en este caso p divide a F_p.

{displaystyle {begin{cases}p=5&Rightarrow pmid F_{p},\pequiv pm 1{pmod {5}}&Rightarrow pmid F_{p-1},\pequiv pm 2{pmod {5}}&Rightarrow pmid F_{p+1}.end{cases}}}

Estos casos se pueden combinar en una fórmula única, no por partes, utilizando el símbolo de Legendre:

{displaystyle pmid F_{p-left({frac {5}{p}}right)}.}

Pruebas de primalidad

La fórmula anterior se puede utilizar como prueba de primalidad en el sentido de que si

{displaystyle nmid F_{n-left({frac {5}{n}}right)},}

nnnnFibonacci pseudoprimemF_mn

{displaystyle {begin{pmatrix}F_{m+1}&F_{m}\F_{m}&F_{m-1}end{pmatrix}}equiv {begin{pmatrix}1&1\1&0end{pmatrix}}^{m}{pmod {n}}.}

A^m

Primas de Fibonacci

(feminine)

Un primo de Fibonacci es un número de Fibonacci que es primo. Los primeros son:

2, 3, 5, 13, 89, 233, 1597, 28657, 514229,...

Se han encontrado números primos de Fibonacci con miles de dígitos, pero no se sabe si hay infinitos.

F_kn es divisible por F_n, por lo que, además de F₄ = 3, cualquier primo de Fibonacci debe tener un índice primo. Como existen series arbitrariamente largas de números compuestos, también existen series arbitrariamente largas de números compuestos de Fibonacci.

Ningún número de Fibonacci mayor que F₆ = 8 es uno mayor o uno menor que un número primo.

El único número de Fibonacci cuadrado no trivial es 144. Attila Pethő demostró en 2001 que solo hay un número finito de números de Fibonacci de potencia perfecta. En 2006, Y. Bugeaud, M. Mignotte y S. Siksek demostraron que 8 y 144 son las únicas potencias perfectas no triviales.

1, 3, 21 y 55 son los únicos números triangulares de Fibonacci, lo cual fue conjeturado por Vern Hoggatt y probado por Luo Ming.

Ningún número de Fibonacci puede ser un número perfecto. De manera más general, ningún número de Fibonacci que no sea 1 puede ser multiplicado perfecto, y ninguna proporción de dos números de Fibonacci puede ser perfecta.

Primeras divisores

(feminine)

Con las excepciones de 1, 8 y 144 (F₁ = F₂, F₆ y F₁₂) cada número de Fibonacci tiene un factor primo que no es un factor de ningún número de Fibonacci más pequeño (Carmichael& #39;teorema de s). Como resultado, 8 y 144 (F₆ y F₁₂) son los únicos números de Fibonacci que son los producto de otros números de Fibonacci.

La divisibilidad de los números de Fibonacci por un primo p está relacionado con el símbolo Legendre $left({tfrac {p}{5}}right)$ que se evalúa como sigue:

{displaystyle left({frac {p}{5}}right)={begin{cases}0&{text{if }}p=5\1&{text{if }}pequiv pm 1{pmod {5}}\-1&{text{if }}pequiv pm 2{pmod {5}}.end{cases}}}

Si p es un número primo entonces

{displaystyle F_{p}equiv left({frac {p}{5}}right){pmod {p}}quad {text{and}}quad F_{p-left({frac {p}{5}}right)}equiv 0{pmod {p}}.}

Por ejemplo,

{displaystyle {begin{aligned}({tfrac {2}{5}})&=-1,&F_{3}&=2,&F_{2}&=1,\({tfrac {3}{5}})&=-1,&F_{4}&=3,&F_{3}&=2,\({tfrac {5}{5}})&=0,&F_{5}&=5,\({tfrac {7}{5}})&=-1,&F_{8}&=21,&F_{7}&=13,\({tfrac {11}{5}})&=+1,&F_{10}&=55,&F_{11}&=89.end{aligned}}}

No se sabe si existe un primo p tal que

{displaystyle F_{p-left({frac {p}{5}}right)}equiv 0{pmod {p^{2}}}.}

Estos números primos (si los hay) se llamarían números primos Sol-Pared-Sol.

Además, si p ≠ 5 es un número primo impar entonces:

{displaystyle 5{F_{frac {ppm 1}{2}}}^{2}equiv {begin{cases}{tfrac {1}{2}}left(5left({frac {p}{5}}right)pm 5right){pmod {p}}&{text{if }}pequiv 1{pmod {4}}\{tfrac {1}{2}}left(5left({frac {p}{5}}right)mp 3right){pmod {p}}&{text{if }}pequiv 3{pmod {4}}.end{cases}}}

Ejemplo 1. p = 7, en este caso p ≡ 3 (mod 4) y tenemos:

{displaystyle ({tfrac {7}{5}})=-1:qquad {tfrac {1}{2}}left(5({tfrac {7}{5}})+3right)=-1,quad {tfrac {1}{2}}left(5({tfrac {7}{5}})-3right)=-4.}

{displaystyle F_{3}=2{text{ and }}F_{4}=3.}

{displaystyle 5{F_{3}}^{2}=20equiv -1{pmod {7}};;{text{ and }};;5{F_{4}}^{2}=45equiv -4{pmod {7}}}

Ejemplo 2. p = 11, en este caso p ≡ 3 (mod 4) y tenemos:

{displaystyle ({tfrac {11}{5}})=+1:qquad {tfrac {1}{2}}left(5({tfrac {11}{5}})+3right)=4,quad {tfrac {1}{2}}left(5({tfrac {11}{5}})-3right)=1.}

{displaystyle F_{5}=5{text{ and }}F_{6}=8.}

{displaystyle 5{F_{5}}^{2}=125equiv 4{pmod {11}};;{text{ and }};;5{F_{6}}^{2}=320equiv 1{pmod {11}}}

Ejemplo 3. p = 13, en este caso p ≡ 1 (mod 4) y tenemos:

{displaystyle ({tfrac {13}{5}})=-1:qquad {tfrac {1}{2}}left(5({tfrac {13}{5}})-5right)=-5,quad {tfrac {1}{2}}left(5({tfrac {13}{5}})+5right)=0.}

{displaystyle F_{6}=8{text{ and }}F_{7}=13.}

{displaystyle 5{F_{6}}^{2}=320equiv -5{pmod {13}};;{text{ and }};;5{F_{7}}^{2}=845equiv 0{pmod {13}}}

Ejemplo 4. p = 29, en este caso p ≡ 1 (mod 4) y tenemos:

{displaystyle ({tfrac {29}{5}})=+1:qquad {tfrac {1}{2}}left(5({tfrac {29}{5}})-5right)=0,quad {tfrac {1}{2}}left(5({tfrac {29}{5}})+5right)=5.}

{displaystyle F_{14}=377{text{ and }}F_{15}=610.}

{displaystyle 5{F_{14}}^{2}=710645equiv 0{pmod {29}};;{text{ and }};;5{F_{15}}^{2}=1860500equiv 5{pmod {29}}}

Para n impares, todos los divisores primos impares de F_n son congruentes con 1 módulo 4, lo que implica que todos los divisores impares de F_n (como los productos de los divisores primos impares) son congruentes con 1 módulo 4.

Por ejemplo,

{displaystyle F_{1}=1,F_{3}=2,F_{5}=5,F_{7}=13,F_{9}=34=2cdot 17,F_{11}=89,F_{13}=233,F_{15}=610=2cdot 5cdot 61.}

Todos los factores conocidos de los números de Fibonacci F(i) para todos los i < 50000 se recogen en los repositorios correspondientes.

Periodicidad módulo n

Si los miembros de la secuencia de Fibonacci se toman mod n, la secuencia resultante es periódica con un período como máximo 6n. Las longitudes de los períodos para varios n forman los llamados períodos Pisano. Determinar una fórmula general para los períodos de Pisano es un problema abierto, que incluye como subproblema una instancia especial del problema de encontrar el orden multiplicativo de un entero modular o de un elemento en un campo finito. Sin embargo, para cualquier n particular, el período de Pisano se puede encontrar como una instancia de detección de ciclo.

Generalizaciones

La sucesión de Fibonacci es una de las sucesiones conocidas más simples y antiguas definidas por una relación de recurrencia y, específicamente, por una ecuación de diferencia lineal. Todas estas secuencias pueden verse como generalizaciones de la secuencia de Fibonacci. En particular, la fórmula de Binet se puede generalizar a cualquier secuencia que sea una solución de una ecuación en diferencias lineal homogénea con coeficientes constantes.

Algunos ejemplos específicos que están cerca, en cierto sentido, de la secuencia de Fibonacci incluyen:

Generalizar el índice a números negativos para producir los números negafibonacci.
Generalizar el índice a números reales utilizando una modificación de la fórmula de Binet.
Comenzando con otros enteros. Los números de Lucas L₁ = 1, L₂ = 3, y L_n = L_n−1 + L_n−2. Las secuencias libres utilizan la recursión Fibonacci con otros puntos de partida para generar secuencias en las que todos los números están compuestos.
Dejar que un número sea una función lineal (excepto la suma) de los 2 números anteriores. Los números de Pell tienen P_n = 2P_{n − 1} + P_{n − 2}. Si el coeficiente del valor anterior se asigna un valor variable x, el resultado es la secuencia de polinomios Fibonacci.
No añadir los números inmediatamente anteriores. La secuencia de Padovan y los números de Perrin tienen P()n) P()n − 2) + P()n - 3).
Generando el siguiente número añadiendo 3 números (números de tribonacci), 4 números (números de tetranacci), o más. Las secuencias resultantes se conocen como n-Step Fibonacci números.

Aplicaciones

Matemáticas

Los números de Fibonacci son las sumas de las diagonales "compartidas" (muestras en rojo) del triángulo de Pascal.

Los números de Fibonacci ocurren en las sumas de "superficial" diagonales en el triángulo de Pascal (ver coeficiente binomial):

La función generadora se puede expandir a

{displaystyle {frac {x}{1-x-x^{2}}}=x+x^{2}(1+x)+x^{3}(1+x)^{2}+dots +x^{k+1}(1+x)^{k}+dots =sum limits _{n=0}^{infty }F_{n}x^{n}}

x^{n}

{displaystyle F_{n}=sum _{k=0}^{leftlfloor {frac {n-1}{2}}rightrfloor }{binom {n-k-1}{k}}.}

Para ver cómo se usa la fórmula, podemos ordenar las sumas por el número de términos presentes:

$5$	$= 1+1+1+1$
	$= 2+1+1+1$	$= 1+2+1+1$	$= 1+1+2+1$	$= 1+1+1+2$
	$= 2+2+1$	$= 2+1+2$	$= 1+2+2$

que es ${displaystyle {binom {5}{0}}+{binom {4}{1}}+{binom {3}{2}}}$ , donde estamos eligiendo las posiciones k dos de n-k-1 términos.

Uso de la secuencia Fibonacci para contar {1, 2}-restricted composiciones

Estos números también dan la solución a ciertos problemas enumerativos, el más común de los cuales es el de contar el número de formas de escribir un número determinado $n$ como una suma ordenada de 1s y 2s (llamadas composiciones); hay $F n + 1$ maneras de hacer esto (equivalentemente, también es el número de dominos de las baldosas de los $2times n$ rectángulo). Por ejemplo, hay $F 5+1 = F 6 = 8$ maneras que uno puede subir una escalera de 5 pasos, tomando uno o dos pasos a la vez:

$5$	$= 1+1+1+1$	$= 2+1+1+1$	$= 1+2+1+1$	$= 1+1+2+1$	$= 2+2+1$
	$= 1+1+1+2$	$= 2+1+2$	$= 1+2+2$

La figura muestra que 8 se puede descomponer en 5 (el número de formas de subir 4 escalones, seguido de un solo escalón) más 3 (el número de formas de subir 3 escalones, seguido de un escalón doble). El mismo razonamiento se aplica recursivamente hasta un solo escalón, del cual sólo hay un camino para subir.

Los números de Fibonacci se pueden encontrar de diferentes maneras entre el conjunto de cadenas binarias, o de manera equivalente, entre los subconjuntos de un conjunto dado.

El número de cuerdas binarias de longitud $n$ sin consecutivo $1$ s es el número de Fibonacci $F n +2$ . Por ejemplo, de las 16 cadenas binarias de la longitud 4, hay $F 6 = 8$ sin consecutivo $1$ s – son 0000, 0001, 0010, 0100, 0101, 1000, 1001, y 1010. Tales cadenas son las representaciones binarias de los números de Fibbinary. Equivalentemente, $F n +2$ es el número de subconjuntos $S$ de ${1,... n}$ sin enteros consecutivos, es decir, aquellos $S$ para la cual ${} i, i + 1} S$ para todos $i$ . Una bijeción con las sumas a n+1 es reemplazar 1 con 0 y 2 con 10Y baja el último cero.
El número de cuerdas binarias de longitud $n$ sin un número impar de consecutivos $1$ s es el número de Fibonacci $F n+1$ . Por ejemplo, de las 16 cadenas binarias de la longitud 4, hay $F 5 = 5$ sin un número impar de consecutivos $1$ s – son 0000, 0011, 0110, 1100, 1111. Equivalentemente, el número de subconjuntos $S$ de ${1,... n}$ sin un número impar de enteros consecutivos es $F n + 1$ . Una bijeción con las sumas a n es reemplazar 1 con 0 y 2 con 11.
El número de cuerdas binarias de longitud $n$ sin un número de consecutivos $0$ o $1$ s $2 F n$ . Por ejemplo, de las 16 cadenas binarias de la longitud 4, hay $2 F 4 = 6$ sin un número de consecutivos $0$ o $1$ s – son 0001, 0111, 0101, 1000, 1010, 1110. Hay una declaración equivalente sobre subconjuntos.
Yuri Matiyasevich fue capaz de demostrar que los números de Fibonacci pueden ser definidos por una ecuación Diofantina, lo que condujo a su resolución el décimo problema de Hilbert.
Los números de Fibonacci son también un ejemplo de una secuencia completa. Esto significa que cada entero positivo puede ser escrito como una suma de números Fibonacci, donde cualquier número se utiliza una vez al máximo.
Además, cada entero positivo puede ser escrito de una manera única como la suma de uno o más distintos números de Fibonacci de tal manera que la suma no incluye ningunos dos números consecutivos de Fibonacci. Esto se conoce como teorema de Zeckendorf, y una suma de los números de Fibonacci que satisface estas condiciones se llama representación de Zeckendorf. La representación Zeckendorf de un número se puede utilizar para derivar su codificación Fibonacci.
Empezando con 5, cada segundo número de Fibonacci es la longitud de la hipotenusa de un triángulo derecho con los lados enteros, o en otras palabras, el mayor número de un triple pitagórico, obtenido de la fórmula ${displaystyle (F_{n}F_{n+3})^{2}+(2F_{n+1}F_{n+2})^{2}={F_{2n+3}}^{2}.}$ La secuencia de triángulos pitagóricos obtenidos de esta fórmula tiene lados de longitudes (3,4,5), (5,12,13), (16,30,34), (39,80,89),... El lado medio de cada uno de estos triángulos es la suma de los tres lados del triángulo anterior.
El cubo Fibonacci es un gráfico no dirigido con un número de nodos Fibonacci que se ha propuesto como topología de red para la computación paralela.
Los números de Fibonacci aparecen en la lema del anillo, utilizado para probar las conexiones entre el teorema de embalaje del círculo y los mapas conformales.

Informática

Fibonacci árbol de altura 6. Factores de equilibrio verde; alturas rojas.
Las llaves de la columna izquierda son números Fibonacci.

Los números de Fibonacci son importantes en el análisis computacional de tiempo de ejecución del algoritmo de Euclid para determinar el mayor divisor común de dos enteros: la peor entrada de caso para este algoritmo es un par de números de Fibonacci consecutivos.
Los números de Fibonacci se utilizan en una versión de polifase del algoritmo de tipo de fusión en la que una lista no surgida se divide en dos listas cuyas longitudes corresponden a los números de Fibonacci secuencial – dividiendo la lista para que las dos partes tengan longitudes en la proporción aproximada φ. En el caso de la fusión de polifase se describió una aplicación de cinta-drive El arte de la programación informática.
Un árbol Fibonacci es un árbol binario cuyos árboles infantiles (recursivamente) difieren en altura por exactamente 1. Por lo tanto es un árbol AVL, y uno con los más pocos nodos para una altura dada — el árbol AVL más "thinnest". Estos árboles tienen una serie de vértices que es un número Fibonacci menos uno, un hecho importante en el análisis de árboles AVL.
Los números de Fibonacci son usados por algunos generadores de números de seudorandom.
Los números de Fibonacci surgen en el análisis de la estructura de datos del montón de Fibonacci.
Un método de optimización unidimensional, llamado técnica de búsqueda Fibonacci, utiliza números Fibonacci.
La serie de números Fibonacci se utiliza para la compresión de pérdida opcional en el formato de archivo de audio IFF 8SVX utilizado en los ordenadores Amiga. La serie número compone la onda de audio original similar a los métodos logarítmicos como μ-law.
Algunos equipos ágiles utilizan una serie modificada llamada "Modified Fibonacci Series" en la planificación del poker, como una herramienta de estimación. Planeamiento Poker es una parte formal del Marco Agile Scaled.
Codificación de Fibonacci
Codificación NegaFibonacci

Naturaleza

Cabeza de manzanilla amarilla mostrando el arreglo en 21 espirales (azul) y 13 (aqua). Tales arreglos con números de Fibonacci consecutivos aparecen en una amplia variedad de plantas.

Las secuencias de Fibonacci aparecen en escenarios biológicos, como la ramificación de los árboles, la disposición de las hojas en un tallo, los frutos de una piña, el florecimiento de una alcachofa, un helecho que se despliega y la disposición de una piña, y el árbol genealógico de abejas Kepler señaló la presencia de la secuencia de Fibonacci en la naturaleza, usándola para explicar la forma pentagonal (relacionada con la proporción áurea) de algunas flores. Las margaritas de campo suelen tener pétalos en cuentas de números de Fibonacci. En 1830, K. F. Schimper y A. Braun descubrieron que las parásitas (filotaxis en espiral) de las plantas se expresaban con frecuencia como fracciones que involucraban números de Fibonacci.

Przemysław Prusinkiewicz avanzó la idea de que las instancias reales pueden entenderse en parte como la expresión de ciertas restricciones algebraicas sobre grupos libres, específicamente como ciertas gramáticas de Lindenmayer.

Ilustración del modelo de Vogel para

n = 1... 500

Helmut Vogel propuso un modelo para el patrón de flores en la cabeza de un girasol [de] en 1979. Esto tiene la forma

{displaystyle theta ={frac {2pi }{varphi ^{2}}}n, r=c{sqrt {n}}}

donde $n$ es el número índice del florete y $c$ es un factor de escala constante; los floretes se encuentran así en la espiral de Fermat. El ángulo de divergencia, aproximadamente 137,51°, es el ángulo áureo, que divide el círculo en proporción áurea. Debido a que esta proporción es irracional, ningún florete tiene un vecino exactamente en el mismo ángulo desde el centro, por lo que los floretes se empaquetan eficientemente. Debido a que las aproximaciones racionales a la proporción áurea tienen la forma $F (j): F (j + 1)$ , los vecinos más cercanos del florete número $n$ son los de <span class="texhtml" n ± F(j) para algún índice $j$ , que depende de $r$ , la distancia desde el centro. Los girasoles y flores similares suelen tener espirales de floretes en sentido horario y antihorario en la cantidad de números de Fibonacci adyacentes, normalmente contados por el rango más externo de radios.

Los números de Fibonacci también aparecen en las genealogías de las abejas melíferas idealizadas, de acuerdo con las siguientes reglas:

Si un óvulo es colocado por una hembra no calentada, pica una abeja macho o dron.
Si, sin embargo, un óvulo fue fertilizado por un macho, pica a una hembra.

Por lo tanto, una abeja macho siempre tiene un padre y una abeja hembra tiene dos. Si uno rastrea el pedigrí de cualquier abeja macho (1 abeja), tiene 1 padre (1 abeja), 2 abuelos, 3 bisabuelos, 5 tatarabuelos, y así sucesivamente. Esta secuencia de números de padres es la secuencia de Fibonacci. El número de antepasados en cada nivel, $F n$ , es el número de antepasados femeninos, que es $F n -1$ , más el número de antepasados masculinos, que es $F n -2$ . Esto es bajo la suposición poco realista de que los ancestros en cada nivel no están relacionados.

El número de posibles antepasados en la línea de herencia cromosoma X en una generación ancestral dada sigue la secuencia de Fibonacci. (Después de Hutchison, L. "Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships".)

Se ha notado que el número de posibles ancestros en la línea humana de herencia cromosoma X en una determinada generación ancestral también sigue la secuencia de Fibonacci. Un individuo masculino tiene un cromosoma X, que recibió de su madre, y un cromosoma Y, que recibió de su padre. El macho cuenta como el "origen" de su propio cromosoma X ( $F_{1}=1$ ), y en la generación de sus padres, su cromosoma X vino de un solo padre ( $F_{2}=1$ ). La madre del varón recibió un cromosoma X de su madre (la abuela materna del hijo), y uno de su padre (el abuelo materno del hijo), por lo que dos abuelos contribuyeron al cromosoma X del descendiente masculino (cromosoma X) ${displaystyle F_{3}=2}$ ). El abuelo materno recibió su cromosoma X de su madre, y la abuela materna recibió cromosomas X de ambos padres, por lo que tres bisabuelos contribuyeron al cromosoma X del descendiente masculino (Cromosoma X) ${displaystyle F_{4}=3}$ ). Cinco bisabuelos grandes contribuyeron al cromosoma X del descendiente masculino ( ${displaystyle F_{5}=5}$ ), etc. (Esto supone que todos los antepasados de un descendiente dado son independientes, pero si alguna genealogía se rastrea lo suficientemente atrás en el tiempo, los antepasados comienzan a aparecer en múltiples líneas de la genealogía, hasta que finalmente un fundador de la población aparece en todas las líneas de la genealogía).

Otro

En óptica, cuando un rayo de luz brilla en un ángulo a través de dos placas transparentes apiladas de diferentes materiales de diferentes índices refractivos, puede reflejar tres superficies: la superficie superior, media y inferior de las dos placas. El número de caminos diferentes que tienen $k$ reflexiones, para $k ■ 1$ , es el $k$ el número Fibonacci. (Sin embargo, cuando $k = 1$ , hay tres caminos de reflexión, no dos, uno para cada una de las tres superficies.)
Los niveles de retracemento de Fibonacci se utilizan ampliamente en el análisis técnico para el comercio de mercados financieros.
Dado que el factor de conversión 1.609344 para millas a kilómetros está cerca de la relación de oro, la descomposición de distancia en millas en una suma de los números Fibonacci se convierte en casi la suma de kilómetro cuando los números Fibonacci son reemplazados por sus sucesores. Este método equivale a un registro de número de radio 2 en base dorada φ siendo cambiado. Para convertir de kilómetros a millas, cambia el registro por la secuencia de Fibonacci.
Los valores medidos de voltajes y corrientes en el circuito de cadena de resistencia infinita (también llamado escalera de resistencia o circuito de serie infinita) siguen la secuencia de Fibonacci. Los resultados intermedios de añadir la serie alterna y las resistencias paralelas producen fracciones compuestas por números consecutivos de Fibonacci. La resistencia equivalente de todo el circuito equivale a la relación de oro.
Brasch et al. 2012 muestran cómo una secuencia generalizada de Fibonacci también puede conectarse al campo de la economía. En particular, se muestra cómo una secuencia generalizada de Fibonacci entra en la función de control de los problemas de optimización dinámica finita-horizona con un estado y una variable de control. El procedimiento se ilustra en un ejemplo a menudo conocido como el modelo de crecimiento económico Brock-Mirman.
Mario Merz incluyó la secuencia de Fibonacci en algunas de sus obras de arte a partir de 1970.
Joseph Schillinger (1895–1943) desarrolló un sistema de composición que utiliza intervalos de Fibonacci en algunas de sus melodías; las vio como contraparte musical a la elaborada armonía evidente dentro de la naturaleza. Ver también ratio de oro § Música.

Contenido relacionado

Más resultados...