Mónada (teoría de categorías)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Operación en álgebra y matemáticas

En teoría de categorías, una rama de las matemáticas, una mónada (también triple, tríada, construcción estándar y construcción fundamental) es un monoide en la categoría de endofunctores de alguna categoría fija. Un endofunctor es un funtor que asigna una categoría a sí mismo, y una mónada es un endofunctor junto con dos transformaciones naturales necesarias para cumplir ciertas condiciones de coherencia. Las mónadas se utilizan en la teoría de pares de funtores adjuntos y generalizan operadores de cierre en conjuntos parcialmente ordenados a categorías arbitrarias. Las mónadas también son útiles en la teoría de tipos de datos, la semántica denotacional de los lenguajes de programación imperativos y en los lenguajes de programación funcionales, permitiendo que los lenguajes con estados no mutables hagan cosas como simular bucles for; ver Monad (programación funcional).

Introducción y definición

Una monada es un cierto tipo de endofunctor. Por ejemplo, si $F$ y $G$ son un par de funerarios adjuntos, con $F$ a la izquierda $G$ , entonces la composición $Gcirc F$ es una monada. Si $F$ y $G$ son functores inversos, la monada correspondiente es el functor de identidad. En general, las disposiciones no son equivalencias, sino categorías de diferentes naturalezas. La teoría de la monada importa como parte del esfuerzo para capturar lo que es que adjunciones 'preserve'. La otra mitad de la teoría, de lo que se puede aprender de la consideración de $Fcirc G$ , se discute bajo la teoría dual de comonads.

Definición formal

A lo largo de este artículo $C$ denota una categoría. A monad on $C$ consiste en un endofunctor $Tcolon Cto C$ junto con dos transformaciones naturales: $eta colon 1_{C}to T$ (donde) $1_{C}$ denota el funerario de identidad en $C$ ) y $mu colon T^{2}to T$ (donde) $T^{2}$ es el functor $Tcirc T$ desde $C$ a $C$ ). Estos son necesarios para cumplir las siguientes condiciones (a veces llamadas condiciones de coherencia):

$mu circ Tmu =mu circ mu T$ (como transformaciones naturales $T^{3}to T$ ); aquí $Tmu$ y $mu T$ están formados por "composición horizontal"
$mu circ Teta =mu circ eta T=1_{T}$ (como transformaciones naturales $Tto T$ ; aquí $1_{T}$ denota la transformación de la identidad $T$ a $T$ ).

Podemos reescribir estas condiciones usando los siguientes diagramas conmutativos:

Véase el artículo sobre las transformaciones naturales para la explicación de las notaciones $Tmu$ y $mu T$ , o ver debajo de los diagramas conmutativos no usando estas nociones:

El primer axioma es similar a la asociación en monoides si pensamos $mu$ como la operación binaria del monoide, y el segundo axioma es similar a la existencia de un elemento de identidad (que pensamos como $eta$ ). De hecho, una monada sobre $C$ puede ser definido como un monoide en la categoría $mathbf {End} _{C}$ cuyos objetos son los endofundores de $C$ y cuyos morfismos son las transformaciones naturales entre ellos, con la estructura monoidal inducida por la composición de endofunctores.

La mónada del conjunto de poderes

El el poder monad es un monad ${mathcal {P}}$ en la categoría $mathbf {Set}$ : Para un set $A$ Deja $T(A)$ ser el conjunto de poder $A$ y para una función $fcolon Ato B$ Deja $T(f)$ ser la función entre los conjuntos de potencia inducidos por tomar imágenes directas bajo $f$ . Para cada juego $A$ , tenemos un mapa $eta _{A}colon Ato T(A)$ , que asigna a cada $ain A$ el singleton ${a}$ . La función

mu _{A}colon T(T(A))to T(A)

lleva un conjunto de conjuntos a su unión. Estos datos describen una mónada.

Observaciones

Los axiomas de una monada son formalmente similares a los axiomas monoide. De hecho, las monadas son casos especiales de monoides, es decir, son precisamente los monoides entre endofunctores ${displaystyle operatorname {End} (C)}$ , que está equipado con la multiplicación dada por la composición de endofunctores.

La composición de las cuentas no es, en general, una monada. Por ejemplo, el functor de doble potencia ${displaystyle {mathcal {P}}circ {mathcal {P}}}$ no admite ninguna estructura monad.

Comonadas

La definición dual categórica es una definición formal de una comonad (o cotriple); esto se puede decir rápidamente en los términos que un comonad para una categoría $C$ es una monada para la categoría opuesta $C^{mathrm {op} }$ . Por lo tanto, es un functor $U$ desde $C$ a sí mismo, con un conjunto de axiomas para counit y comultiplicación que provienen de invertir las flechas en todas partes en la definición que se acaba de dar.

Las mónadas son para los monoides lo que las comonadas son para los comonoides. Cada conjunto es un comonoide de una manera única, por lo que los comonoides son menos familiares en álgebra abstracta que los monoides; sin embargo, los comonoides en la categoría de espacios vectoriales con su producto tensorial habitual son importantes y ampliamente estudiados bajo el nombre de coalgebras.

Historia terminológica

La noción de mónada fue inventada por Roger Godement en 1958 con el nombre de "construcción estándar". Monad ha sido denominada "construcción de doble estándar", "triple", "monoide" y "tríada". El término "mónada" es utilizado a más tardar en 1967, por Jean Bénabou.

Ejemplos

Identidad

El functor de identidad en una categoría $C$ es una monada. Su multiplicación y unidad son la función de identidad en los objetos $C$ .

Mónadas que surgen de adjunciones

Cualquier complemento

{displaystyle F:Crightleftarrows D:G}

da lugar a una mónada en C. Esta construcción muy extendida funciona de la siguiente manera: el endofunctor es el compuesto

{displaystyle T=Gcirc F.}

Este endofunctor se ve rápidamente como una monada, donde el mapa de la unidad se deriva del mapa de la unidad ${displaystyle operatorname {id} _{C}to Gcirc F}$ de la adjunción, y el mapa de multiplicación se construye utilizando el mapa de counidad de la adjunción:

{displaystyle T^{2}=Gcirc Fcirc Gcirc Fxrightarrow {Gcirc {text{counit}}circ F} Gcirc F=T.}

De hecho, cualquier monada se puede encontrar como un adjunto explícito de functores utilizando la categoría Eilenberg-Moore $C^{T}$ (la categoría de $T$ - álgebras).

Doble dualización

La mónada de doble dualización, para un campo fijo k surge de la adjunción

{displaystyle (-)^{*}:mathbf {Vect} _{k}rightleftarrows mathbf {Vect} _{k}^{op}:(-)^{*}}

donde ambos functores son dados por el envío de un espacio vectorial V su espacio vectorial dual ${displaystyle V^{*}:=operatorname {Hom} (V,k)}$ . La monada asociada envía un espacio vectorial V a su doble dual $V^{{**}}$ . Esta monada es discutida, en mayor generalidad, por Kock (1970).

Operadores de cierre en conjuntos parcialmente ordenados

Para categorías derivadas de conjuntos parcialmente ordenados $(P,leq)$ (con un solo morfismo de $x$ a $y$ si $xleq y$ ), entonces el formalismo se vuelve mucho más simple: pares unidos son conexiones Galois y las monadas son operadores de cierre.

Complementos libres y olvidadizos

Por ejemplo, vamos $G$ ser el functor olvidadizo de la categoría Grp de grupos a la categoría Juego de conjuntos, y dejar $F$ ser el free group functor de la categoría de sets a la categoría de grupos. Entonces... $F$ es la unión izquierda de $G$ . En este caso, la monada asociada $T=Gcirc F$ toma un set $X$ y devuelve el conjunto subyacente del grupo libre $mathrm {Free} (X)$ . El mapa unitario de esta monada es dado por los mapas

{displaystyle Xto T(X)}

incluido el conjunto $X$ en el set $mathrm {Free} (X)$ en la forma natural, como cuerdas de longitud 1. Además, la multiplicación de esta monada es el mapa

{displaystyle T(T(X))to T(X)}

hecho de una concatenación natural o 'aplanamiento' de 'cadenas de cuerdas'. Esto equivale a dos transformaciones naturales. El ejemplo anterior sobre grupos libres se puede generalizar a cualquier tipo de álgebra en el sentido de una variedad de álgebras del álgebra universal. Por tanto, cada tipo de álgebra da lugar a una mónada en la categoría de conjuntos. Es importante destacar que el tipo de álgebra se puede recuperar de la mónada (como categoría de las álgebras de Eilenberg-Moore), por lo que las mónadas también pueden verse como variedades generalizadoras de álgebras universales.

Otra monada que surge de una adjunción es cuando $T$ es el endofunctor en la categoría de espacios vectoriales que mapea un espacio vectorial $V$ a su álgebra tensor $T(V)$ , y que mapas lineales mapas a su producto tensor. Entonces tenemos una transformación natural correspondiente a la incrustación de $V$ en su álgebra tensor, y una transformación natural correspondiente al mapa desde ${displaystyle T(T(V))}$ a $T(V)$ obtenido simplemente ampliando todos los productos tensores.

Mónadas de codensidad

En condiciones suaves, los functores que no admiten un adjunto izquierdo también dan lugar a una mónada, la llamada mónada de codensidad. Por ejemplo, la inclusión

{displaystyle mathbf {FinSet} subset mathbf {Set} }

no admite adjunto izquierdo. Su mónada de codensidad es la mónada en conjuntos que envía cualquier conjunto X al conjunto de ultrafiltros en X. Este y otros ejemplos similares se analizan en Leinster (2013).

Mónadas utilizadas en semántica denotacional

Las siguientes mónadas sobre la categoría de conjuntos se utilizan en la semántica denotacional de lenguajes de programación imperativos, y construcciones análogas se utilizan en la programación funcional.

La mónada tal vez

El endofunctor de la mónada tal vez o parcialidad añade un punto disjunto:

{displaystyle (-)_{*}:mathbf {Set} to mathbf {Set} }

{displaystyle Xmapsto Xcup {*}}

La unidad es dada por la inclusión de un conjunto $X$ en ${displaystyle X_{*}}$ :

{displaystyle eta _{X}:Xto X_{*}}

xmapsto x

Los mapas de multiplicación elementos de $X$ a ellos mismos, y los dos puntos descomunales ${displaystyle (X_{*})_{*}}$ a la ${displaystyle X_{*}}$ .

Tanto en programación funcional como en semántica denotacional, la mónada quizás modela cálculos parciales, es decir, cálculos que pueden fallar.

La mónada estatal

Dado un conjunto $S$ , el endofuntor del estado monad mapas cada conjunto $X$ al conjunto de funciones ${displaystyle Sto Stimes X}$ . El componente de la unidad en $X$ mapas cada elemento $xin X$ a la función

{displaystyle eta _{X}(x):Sto Stimes X}

{displaystyle smapsto (s,x)}

La multiplicación mapea la función ${displaystyle f:Sto Stimes (Sto Stimes X),smapsto (s',f')}$ a la función

{displaystyle mu _{X}(f):Sto Stimes X}

{displaystyle smapsto f'(s')}

En programación funcional y semántica denotacional, la mónada de estado modela cálculos con estado.

La mónada ambiental

Dado un conjunto $E$ , el endofuntor del lector o el medio ambiente monad mapas cada conjunto $X$ al conjunto de funciones $Eto X$ . Así, el endofunctor de esta monada es exactamente el functor hom ${displaystyle mathrm {Hom} (E,-)}$ . El componente de la unidad en $X$ mapas cada elemento $xin X$ a la función constante ${displaystyle emapsto x}$ .

En programación funcional y semántica denotacional, la mónada ambiental modela cálculos con acceso a algunos datos de solo lectura.

La lista y conjunto de mónadas

La lista o mónada de no determinismo asigna un conjunto X al conjunto de secuencias finitas (es decir, listas) con elementos de X. La unidad asigna un elemento x en X a la lista singleton [x]. La multiplicación concatena una lista de listas en una sola lista.

En programación funcional, la mónada de lista se utiliza para modelar cálculos no deterministas. La mónada de conjunto de potencias covariante también se conoce como mónada de conjunto y también se utiliza para modelar cálculos no deterministas.

Álgebras para una mónada

Dado un monad $(T,etamu)$ en una categoría $C$ , es natural considerar $T$ - álgebras, es decir, objetos de $C$ actuó por $T$ de una manera que es compatible con la unidad y la multiplicación de la monada. Más formalmente, un $T$ - álgebra $(x,h)$ es un objeto $x$ de $C$ junto con una flecha $hcolon Txto x$ de $C$ llamado estructura mapa del álgebra tal que los diagramas

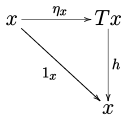desplazamiento.

Un morfismo $fcolon (x,h)to (x',h')$ de $T$ - álgebras es una flecha $fcolon xto x'$ de $C$ tal que el diagrama

Saludos. $T$ - álgebras forman una categoría llamada el Categoría Eilenberg-Moore y denotado por $C^{T}$ .

Ejemplos

Álgebras sobre la mónada de grupo libre

Por ejemplo, para el grupo libre monad discutido anteriormente, a $T$ - álgebra es un conjunto $X$ junto con un mapa del grupo libre generado por $X$ hacia $X$ sujeto a condiciones de asociación y unicidad. Tal estructura equivale a decir que $X$ es un grupo en sí.

Álgebras sobre la mónada de distribución

Otro ejemplo es el distribución monad ${mathcal {D}}$ en la categoría de sets. Se define enviando un conjunto $X$ al conjunto de funciones ${displaystyle f:Xto [0,1]}$ con apoyo finito y tal que su suma es igual a $1$ . En la notación de configuración, este es el conjunto

<math alttext="{displaystyle {mathcal {D}}(X)=left{f:Xto [0,1]:{begin{matrix}#{text{supp}}(f)D()X)={}f:X→ → [0,1]:# # Supp()f).+JUEGO JUEGO .. x▪ ▪ Xf()x)=1}{displaystyle {Mathcal {D}(X)=left{f:Xto [0,1]:{begin{matrix}#{text{supp}(f) meant+infty \sum _{xin X}f(x)=1end{matrix}right}<img alt="{displaystyle {mathcal {D}}(X)=left{f:Xto [0,1]:{begin{matrix}#{text{supp}}(f)

{displaystyle x+_{r}y}

{displaystyle rin [0,1]}

{displaystyle rx+(1-r)y}

Álgebras sobre la mónada simétrica

Otro ejemplo útil de una monada es el functor de álgebra simétrica en la categoría de $R$ -módulos para un anillo conmutativo $R$ .

{displaystyle {text{Sym}}^{bullet }(-):{text{Mod}}(R)to {text{Mod}}(R)}

R

M

{displaystyle {text{Sym}}^{bullet }(M)=bigoplus _{k=0}^{infty }{text{Sym}}^{k}(M)}

{displaystyle {text{Sym}}^{0}(M)=R}

{displaystyle {text{Sym}}^{bullet }(R^{oplus n})cong R[x_{1},ldotsx_{n}]}

R

R

{displaystyle {text{Alt}}^{bullet }(-)}

{displaystyle T^{bullet }(-)}

R

R

{displaystyle {begin{aligned}{text{Alt}}^{bullet }(R^{oplus n})&=R(x_{1},ldotsx_{n})\{text{T}}^{bullet }(R^{oplus n})&=Rlangle x_{1},ldotsx_{n}rangle end{aligned}}}

R

n

R

n

Álgebras conmutativas en espectros de anillos E-infinito

Hay una construcción analógica para commutative $mathbb {S}$ - álgebras^{pg 113} que proporciona $A$ - álgebras para un conmutador $mathbb {S}$ - álgebra $A$ . Si ${displaystyle {mathcal {M}}_{A}}$ es la categoría de $A$ -módulos, luego el functor ${displaystyle mathbb {P}:{mathcal {M}}_{A}to {mathcal {M}}_{A}}$ es la monada dada por

{displaystyle mathbb {P} (M)=bigvee _{jgeq 0}M^{j}/Sigma _{j}}

{displaystyle M^{j}=Mwedge _{A}cdots wedge _{A}M}

j

{displaystyle {mathcal {C}}_{A}}

A

Mónadas y adjunciones

Como se mencionó anteriormente, cualquier adjunción da lugar a una mónada. Por el contrario, cada mónada surge de alguna adjunción, a saber, la adjunción libre-olvidable.

{displaystyle T(-):Crightleftarrows C^{T}:{text{forget}}}

cuya unión izquierda envía un objeto X gratis T- álgebra T()X). Sin embargo, generalmente hay varias adjunciones distintas que dan lugar a una monada: $mathbf {Adj} (C,T)$ ser la categoría cuyos objetos son las adjunciones $(F,G,e,varepsilon)$ tales que $(GF,e,Gvarepsilon F)=(T,etamu)$ y cuyas flechas son los morfismos de las adjunciones que son la identidad en $C$ . Luego el adjunto libre-olvidado que implica la categoría Eilenberg-Moore $C^{T}$ es un objeto terminal en $mathbf {Adj} (C,T)$ . Un objeto inicial es la categoría Kleisli, que es por definición la subcategoría completa de $C^{T}$ consiste sólo en libre T- álgebras, es decir, T- álgebras de la forma $T(x)$ para algún objeto x de C.

Adjunciones monádicas

Dado cualquier adjunción ${displaystyle (F:Cto D,G:Dto C,etavarepsilon)}$ con monad asociado T, el functor G se puede considerar como

{displaystyle D{stackrel {tilde {G}}{to }}C^{T}{stackrel {text{forget}}{to }}C,}

i.e., G()Y) puede ser naturalmente dotado con un T- estructura álgebra para cualquier Y dentro D. La adjunción se llama monadic adjuntion si el primer functor ${tilde {G}}$ cede una equivalencia de categorías entre D y la categoría Eilenberg-Moore $C^{T}$ . Por extensión, un functor $Gcolon Dto C$ se dice que monadic si tiene una unión izquierda $F$ formando una adjunción monadica. Por ejemplo, la adjunción libre-olvidada entre grupos y conjuntos es monadic, ya que los álgebras sobre la monada asociada son grupos, como se mencionó anteriormente. En general, sabiendo que un adjunto es monadic permite reconstruir objetos en D fuera de objetos en C y el T- acción.

Did you mean:

Beck 's monadicity theorem

El teorema de monádica de Beck da una condición necesaria y suficiente para que una adjunción sea monádica. Una versión simplificada de este teorema establece que G es monádico si es conservador (o G refleja isomorfismos, es decir, un morfismo en D es un isomorfismo si y sólo si su imagen bajo G es un isomorfismo en C) y C tiene y G conserva coecualizadores.

Por ejemplo, el functor olvidadizo de la categoría de espacios compactos de Hausdorff a conjuntos es monádico. Sin embargo, el functor olvidadizo de todos los espacios topológicos a conjuntos no es conservador ya que existen mapas biyectivos continuos (entre espacios no compactos o no de Hausdorff) que no llegan a ser homeomorfismos. Por tanto, este funtor olvidadizo no es monádico. La versión dual del teorema de Beck, que caracteriza las conjunciones comonádicas, es relevante en diferentes campos como la teoría del topos y temas de geometría algebraica relacionados con la descendencia. Un primer ejemplo de adjunción comonádica es la adjunción

{displaystyle -otimes _{A}B:mathbf {Mod} _{A}rightleftarrows mathbf {Mod} _{B}:operatorname {forget} }

para un homomorfismo de anillo $Ato B$ entre anillos conmutativos. Este adjunto es comonádico, por el teorema de Beck, si y sólo si B es fielmente plano como A- Bien. Así, permite descender B-módulos, equipados con un datum de descenso (es decir, una acción de la comonad dada por la adjunción) a A-módulos. La teoría resultante de la ascendencia fielmente plana es ampliamente aplicada en la geometría algebraica.

Usos

Las mónadas se utilizan en programación funcional para expresar tipos de cálculo secuencial (a veces con efectos secundarios). Consulte las mónadas en programación funcional y el módulo b de Wikibook, más orientado matemáticamente: Haskell/Teoría de categorías.

Las mónadas se utilizan en la semántica denotacional de lenguajes de programación impuros funcionales e imperativos.

En lógica categórica, se ha establecido una analogía entre la teoría de mónada-comónada y la lógica modal a través de operadores de cierre, álgebras interiores y su relación con los modelos de S4 y la lógica intuicionista.

Generalización

Es posible definir las monadas en una 2-categoría $C$ . Monads described above are monads for $C=mathbf {Cat}$ .

Contenido relacionado

Más resultados...