Modelo bohr

AjustarCompartirImprimirCitar

Modelo atómico introducido por Niels Bohr en 1913

El modelo de tarta del átomo de hidrógenoZ = 1) o un iión como hidrógeno ()Z ■ 1), donde el electron cargado negativamente confinado a una cáscara atómica rodea un pequeño núcleo atómico cargado positivamente y donde un electrón salta entre órbitas, está acompañado por una cantidad emitida o absorbida de energía electromagnética (.). Las órbitas en las que el electrón puede viajar se muestran como círculos grises; su radio aumenta como n², donde n es el número cuántico principal. El 3 → 2 la transición representada aquí produce la primera línea de la serie Balmer, y para hidrógeno (Z = 1) resulta en un fotón de longitud de onda 656 nm (luz roja).

En física atómica, el modelo de Bohr o modelo de Rutherford-Bohr, presentado por Niels Bohr y Ernest Rutherford en 1913, es un sistema formado por un núcleo pequeño y denso rodeado de electrones en órbita, similar a la estructura del Sistema Solar, pero con atracción proporcionada por fuerzas electrostáticas en lugar de la gravedad. Llegó después del modelo del sistema solar de Joseph Larmor (1897), el modelo del sistema solar de Jean Perrin (1901), el modelo cúbico (1902), el modelo saturnino de Hantaro Nagaoka (1904), el modelo de budín de ciruelas (1904), el modelo cuántico de Arthur El modelo de Haas (1910), el modelo de Rutherford (1911) y el modelo cuántico nuclear de John William Nicholson (1912). La mejora sobre el modelo de Rutherford de 1911 se refería principalmente a la nueva interpretación física cuántica introducida por Haas y Nicholson, pero abandonando cualquier intento de alinearse con la radiación de la física clásica.

El éxito clave del modelo radica en explicar la fórmula de Rydberg para las líneas de emisión espectral del hidrógeno atómico. Si bien la fórmula de Rydberg se conocía experimentalmente, no obtuvo una base teórica hasta que se introdujo el modelo de Bohr. El modelo de Bohr no solo explicó las razones de la estructura de la fórmula de Rydberg, sino que también proporcionó una justificación para las constantes físicas fundamentales que componen los resultados empíricos de la fórmula.

El modelo de Bohr es un modelo relativamente primitivo del átomo de hidrógeno, en comparación con el modelo del átomo de capa de valencia. Como teoría, se puede derivar como una aproximación de primer orden del átomo de hidrógeno utilizando la mecánica cuántica más amplia y mucho más precisa y, por lo tanto, se puede considerar una teoría científica obsoleta. Sin embargo, debido a su simplicidad y sus resultados correctos para sistemas seleccionados (consulte la aplicación a continuación), el modelo de Bohr todavía se enseña comúnmente para presentar a los estudiantes la mecánica cuántica o los diagramas de niveles de energía antes de pasar a la más precisa, pero más compleja. átomo de la capa de valencia. Arthur Erich Haas propuso originalmente un modelo cuántico relacionado en 1910, pero fue rechazado hasta el Congreso Solvay de 1911, donde se discutió a fondo. La teoría cuántica del período entre el descubrimiento de Planck de la cuántica (1900) y el advenimiento de una mecánica cuántica madura (1925) a menudo se conoce como la vieja teoría cuántica.

Origen

Modelo Bohr en 1921 después de la expansión de Sommerfeld de 1913 modelo que muestra electrones máximos por cáscara con conchas etiquetadas en notación de rayos X

A principios del siglo XX, los experimentos de Ernest Rutherford establecieron que los átomos consistían en una nube difusa de electrones cargados negativamente que rodeaban un núcleo pequeño, denso y cargado positivamente. Dados estos datos experimentales, Rutherford naturalmente consideró un modelo planetario del átomo, el modelo de Rutherford de 1911. Este tenía electrones orbitando un núcleo solar, pero implicaba una dificultad técnica: las leyes de la mecánica clásica (es decir, la fórmula de Larmor) predicen que el electrón liberará radiación electromagnética mientras orbita un núcleo. Debido a que el electrón perdería energía, rápidamente se movería en espiral hacia adentro, colapsando en el núcleo en una escala de tiempo de alrededor de 16 picosegundos. El modelo atómico de Rutherford es desastroso porque predice que todos los átomos son inestables. Además, a medida que el electrón gira en espiral hacia adentro, la emisión aumentaría rápidamente en frecuencia debido a que el período orbital se acortaría, lo que daría como resultado una radiación electromagnética con un espectro continuo. Sin embargo, los experimentos de finales del siglo XIX con descargas eléctricas demostraron que los átomos solo emiten luz (es decir, radiación electromagnética) en ciertas frecuencias discretas. A principios del siglo XX, se esperaba que el átomo explicara las líneas espectrales. En 1897, Lord Rayleigh analizó el problema. Para 1906, dijo Rayleigh, “las frecuencias observadas en el espectro pueden no ser frecuencias de perturbación u oscilación en el sentido ordinario, sino que forman una parte esencial de la constitución original del átomo determinada por las condiciones de estabilidad”.

El esbozo del átomo de Bohr llegó durante el proceso de la primera Conferencia Solvay en 1911 sobre el tema de la radiación y el quanta, en la que estuvo presente el mentor de Bohr, Rutherford. La conferencia de Max Planck terminó con esta observación: “... átomos o electrones sujetos al vínculo molecular obedecerían las leyes de la teoría cuántica”. Hendrik Lorentz en la discusión de la conferencia de Planck planteó la cuestión de la composición del átomo basado en el modelo de Thomson con una gran parte de la discusión alrededor del modelo atómico desarrollado por Arthur Erich Haas. Lorentz explicó que la constante de Planck podría tomarse como determinación del tamaño de los átomos, o que el tamaño de los átomos podría ser tomado para determinar la constante de Planck. Lorentz incluyó comentarios sobre la emisión y absorción de radiación concluyendo que “Se establecerá un estado estacionario en el que el número de electrones que entran en sus esferas es igual al número de los que los abandonan”. En la discusión de lo que podría regular las diferencias energéticas entre los átomos, Max Planck simplemente dijo: “Los intermediarios podrían ser los electrones”. Las discusiones delinearon la necesidad de incluir la teoría cuántica en el átomo y las dificultades en una teoría atómica. Planck en su charla dijo explícitamente: “Para que un oscilador [molécula o átomo] pueda proporcionar radiación de acuerdo con la ecuación, es necesario introducir en las leyes de su operación, como ya hemos dicho al principio de este Informe, una hipótesis física particular que es, en un punto fundamental, en contradicción con la Mecánica clásica, explícita o tácitamente”. El primer artículo de Bohr sobre su modelo atómico cita Planck casi palabra para palabra, diciendo: “Cualquiera que sea la alteración de las leyes de movimiento de los electrones, parece necesario introducir en las leyes en cuestión una cantidad extranjera a la electrodinámica clásica, es decir,. La constante de Planck, o como suele llamarse el quantum elemental de acción”. La nota al pie de página de Bohr es la traducción al francés del Congreso Solvay de 1911, probando que modeló su modelo directamente sobre los procedimientos y principios fundamentales establecidos por Planck, Lorentz, y el modelo de Arthur Haas cuantitativo del átomo que se mencionó diecisiete veces. Lorentz terminó la discusión de la charla de Einstein explicando: “La suposición de que esta energía debe ser múltiples $hnu$ conduce a la siguiente fórmula, donde $n$ es un entero: ${displaystyle qv^{2}=nhnu }$ . Rutherford podría haber esbozado estos puntos a Bohr o darle una copia de los procedimientos ya que los citó y los utilizó como referencia. En una entrevista posterior, Bohr dijo que era muy interesante escuchar los comentarios de Rutherford sobre el Congreso Solvay. Pero Bohr dijo, “Vi los informes reales” del Congreso Solvay.

Luego, en 1912, Bohr se encontró con la teoría del modelo atómico de John William Nicholson que cuantificaba el momento angular como h/2 $π$ . Según una celebración del centenario del átomo de Bohr en la revista Nature, fue Nicholson quien descubrió que los electrones irradian las líneas espectrales a medida que descienden hacia el núcleo y su teoría era tanto nuclear como cuántica. Niels Bohr lo citó en su artículo de 1913 sobre el modelo del átomo de Bohr. Muchos historiadores han destacado la importancia del trabajo del modelo atómico cuántico nuclear de Nicholson sobre el modelo de Bohr.

A continuación, su amigo Hans Hansen le dijo a Bohr que la serie de Balmer se calcula usando la fórmula de Balmer, una ecuación empírica descubierta por Johann Balmer en 1885 que describía las longitudes de onda de algunas líneas espectrales de hidrógeno. Esto fue generalizado aún más por Johannes Rydberg en 1888, lo que resultó en lo que ahora se conoce como la fórmula de Rydberg. Después de esto, declaró Bohr, “todo quedó claro”.

Para superar los problemas del átomo de Rutherford, en 1913 Niels Bohr planteó tres postulados que resumen la mayor parte de su modelo:

El electrón es capaz de girar en ciertas órbitas estables alrededor del núcleo sin irradiar energía, contrariamente a lo que sugiere el electromagnetismo clásico. Estas órbitas estables se llaman órbitas estacionarias y se alcanzan a ciertas distancias discretas del núcleo. El electrón no puede tener otra órbita entre las discretas.
Las órbitas estacionarias se alcanzan a distancias para las cuales el impulso angular del electrón giratorio es un número entero de la constante de Planck reducida: $m_{mathrm {e} }vr=nhbar$ , donde n = 1, 2, 3,... se llama el número cuántico principal, y $▪ = h /2 π$ . El valor más bajo de n es 1; esto da el radio orbital más pequeño posible de 0.0529 nm conocido como el radio Bohr. Una vez que un electrón está en esta órbita más baja, no puede acercarse al núcleo. Partiendo de la regla cuántica del impulso angular como admite Bohr es previamente dada por Nicholson en su papel de 1912, Bohr fue capaz de calcular las energías de las órbitas permitidas del átomo de hidrógeno y otros átomos y iones similares a hidrógeno. Estas órbitas están asociadas con energías definidas y también se llaman conchas de energía o niveles de energía. En estas órbitas, la aceleración del electrón no produce radiación y pérdida de energía. El modelo Bohr de un átomo se basó en la teoría cuántica de la radiación de Planck.
Los electrones sólo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia . determinado por la diferencia energética de los niveles según la relación Planck: ${displaystyle Delta E=E_{2}-E_{1}=hnu }$ , donde h Es constante de Planck.

Otros puntos son:

Como la teoría de Einstein del efecto fotoeléctrico, la fórmula de Bohr asume que durante un salto cuántico discreta la cantidad de energía se irradia. Sin embargo, a diferencia de Einstein, Bohr pegado al clásico Teoría Maxwell del campo electromagnético. La cuantificación del campo electromagnético fue explicada por la discrepancia de los niveles de energía atómica; Bohr no creía en la existencia de fotones.
Según la teoría de Maxwell la frecuencia . de la radiación clásica es igual a la frecuencia de rotación ._# del electrón en su órbita, con armónicos en múltiples enteros de esta frecuencia. Este resultado se obtiene del modelo Bohr para saltos entre niveles de energía E_n y E_n−k cuando k es mucho más pequeño que n. Estos saltos reproducen la frecuencia del k- la armónica de la órbita n. Para valores suficientemente grandes n (llamados estados Rydberg), las dos órbitas involucradas en el proceso de emisión tienen casi la misma frecuencia de rotación, de modo que la frecuencia orbital clásica no es ambigua. Pero para pequeño n (o grande) k), la frecuencia de radiación no tiene una interpretación clásica inequívoca. Esto marca el nacimiento del principio de correspondencia, requiriendo teoría cuántica para estar de acuerdo con la teoría clásica sólo en el límite de grandes números cuánticos.
La teoría Bohr-Kramers-Slater (Teoría BKS) es un intento fallido de extender el modelo Bohr, que viola la conservación de la energía y el impulso en saltos cuánticos, con las leyes de conservación sólo manteniendo en promedio.

La condición de Bohr, de que el momento angular es un múltiplo entero de ħ, fue reinterpretada posteriormente en 1924 por de Broglie como una condición de onda estacionaria: el electrón se describe mediante una onda y un número entero de longitudes de onda debe caber a lo largo de la circunferencia de la órbita del electrón:

{displaystyle nlambda =2pi r.}

Según la hipótesis de de Broglie, las partículas de materia como el electrón se comportan como ondas. La longitud de onda de De Broglie de un electrón es

{displaystyle lambda ={frac {h}{mv}},}

lo que implica que

{displaystyle {frac {nh}{mv}}=2pi r,}

{displaystyle {frac {nh}{2pi }}=mvr,}

Donde ${displaystyle mvr}$ es el impulso angular del electrón orbitante. Escritura $ell$ para este impulso angular, la ecuación anterior se convierte

{displaystyle ell ={frac {nh}{2pi }},}

que es el segundo postulado de Bohr.

Bohr describió el momento angular de la órbita del electrón como 1/2h mientras que la longitud de onda de De Broglie de $λ = h / p$ describió h dividido por el momento del electrón. En 1913, sin embargo, Bohr justificó su regla apelando al principio de correspondencia, sin proporcionar ningún tipo de interpretación ondulatoria. En 1913 no se sospechaba del comportamiento ondulatorio de partículas de materia como el electrón.

En 1925, se propuso un nuevo tipo de mecánica, la mecánica cuántica, en la que el modelo de Bohr de los electrones que se desplazan en órbitas cuantizadas se amplió a un modelo más preciso del movimiento de los electrones. La nueva teoría fue propuesta por Werner Heisenberg. Otra forma de la misma teoría, la mecánica ondulatoria, fue descubierta por el físico austriaco Erwin Schrödinger de forma independiente y mediante un razonamiento diferente. Schrödinger empleó las ondas de materia de De Broglie, pero buscó soluciones de onda de una ecuación de onda tridimensional que describía electrones que estaban obligados a moverse alrededor del núcleo de un átomo similar al hidrógeno, al quedar atrapados por el potencial de la carga nuclear positiva..

Niveles de energía de los electrones

Modelos que representan los niveles de energía de electrones en hidrógeno, helio, litio y neón

El modelo de Bohr da resultados casi exactos solo para un sistema en el que dos puntos cargados orbitan entre sí a velocidades mucho menores que la de la luz. Esto no solo involucra sistemas de un electrón como el átomo de hidrógeno, el helio ionizado individualmente y el litio doblemente ionizado, sino que también incluye los estados de positronio y Rydberg de cualquier átomo donde un electrón está lejos de todo lo demás. Se puede usar para cálculos de transición de rayos X de línea K si se agregan otras suposiciones (consulte la ley de Moseley a continuación). En física de alta energía, se puede utilizar para calcular las masas de mesones de quarks pesados.

El cálculo de las órbitas requiere dos suposiciones.

mecánico clásico

El electrón se mantiene en una órbita circular por atracción electrostática. La fuerza centrípeta es igual a la fuerza Coulomb.

{displaystyle {frac {m_{mathrm {e} }v^{2}}{r}}={frac {Zk_{mathrm {e} }e^{2}}{r^{2}}},}

Donde m_e es la masa del electrón, e es la carga primaria, k_e es la constante de Coulomb y Z es el número atómico del átomo. Se supone aquí que la masa del núcleo es mucho mayor que la masa de electrones (que es una buena suposición). Esta ecuación determina la velocidad del electrón en cualquier radio:

{displaystyle v={sqrt {frac {Zk_{mathrm {e} }e^{2}}{m_{mathrm {e} }r}}}.}

También determina la energía total del electrón en cualquier radio:

{displaystyle E=-{frac {1}{2}}m_{mathrm {e} }v^{2}.}

La energía total es negativa e inversamente proporcional a r. Esto significa que se necesita energía para sacar el electrón orbitante del protón. Para valores infinitos r, la energía es cero, correspondiente a un electron inmóvil infinitamente lejos del protón. La energía total es la mitad de la energía potencial, la diferencia es la energía cinética del electrón. Esto también es cierto para las órbitas no circulares por el teorema virial.

Una regla cuántica

El impulso angular L = m_evr es un número entero de ▪:

{displaystyle m_{mathrm {e} }vr=nhbar.}

Derivación

Si un electrón en un átomo se mueve en una órbita con período T, clásicamente la radiación electromagnética se repetirá en cada período orbital. Si el acoplamiento al campo electromagnético es débil, de modo que la órbita no decae mucho en un ciclo, la radiación se emitirá en un patrón que se repite cada período, de modo que la transformada de Fourier tendrá frecuencias que son solo múltiplos de 1/T. Esta es la ley de radiación clásica: las frecuencias emitidas son múltiplos enteros de 1/T.

En la mecánica cuántica, esta emisión debe ser en cuantos de luz, de frecuencias que consisten en múltiplos enteros de 1/T, por lo que la mecánica clásica es una descripción aproximada en números cuánticos grandes. Esto significa que el nivel de energía correspondiente a una órbita clásica de período 1/T debe tener niveles de energía cercanos que difieren en energía por h/T, y deben estar igualmente espaciados cerca de ese nivel,

{displaystyle Delta E_{n}={frac {h}{T(E_{n})}}.}

Bohr se preocupaba de si la energía espaciaba 1/T debe ser mejor calculado con el período del estado de energía $E_{n}$ , o $E_{n+1}$ , o algún promedio - en retrospectiva, este modelo es sólo la aproximación semiclásica líder.

Bohr consideró órbitas circulares. Clásicamente, estas órbitas deben decaer en círculos más pequeños cuando se emiten fotones. El espaciado de nivel entre órbitas circulares se puede calcular con la fórmula de correspondencia. Para un átomo de hidrógeno, las órbitas clásicas tienen un período T determinado por la tercera ley de Kepler a escala como r^3/2. La escala de energía es 1/r, por lo que la fórmula de espaciado entre niveles equivale a

{displaystyle Delta Epropto {frac {1}{r^{3/2}}}propto E^{3/2}.}

Es posible determinar los niveles de energía bajando recursivamente órbita a órbita, pero hay un atajo.

El impulso angular L de las escalas de órbita circular $sqrt{r}$ . La energía en términos del impulso angular es entonces

{displaystyle Epropto {frac {1}{r}}propto {frac {1}{L^{2}}}.}

Suponiendo, con Bohr, que los valores cuantificados de L están igualmente espaciados, el espacio entre las energías vecinas es

{displaystyle Delta Epropto {frac {1}{(L+hbar)^{2}}}-{frac {1}{L^{2}}}approx -{frac {2hbar }{L^{3}}}propto -E^{3/2}.}

Esto es lo deseado para momentos angulares igualmente espaciados. Si uno hiciera un seguimiento de las constantes, el espaciado sería ħ, por lo que el momento angular debería ser un múltiplo entero de ħ,

{displaystyle L={frac {nh}{2pi }}=nhbar.}

Así es como Bohr llegó a su modelo.

Sustituir la expresión para la velocidad da una ecuación para r en términos de n:

{displaystyle m_{text{e}}{sqrt {dfrac {k_{text{e}}Ze^{2}}{m_{text{e}}r}}}r=nhbar}

para que el radio de órbita permitido en cualquier n es

{displaystyle r_{n}={frac {n^{2}hbar ^{2}}{Zk_{mathrm {e} }e^{2}m_{mathrm {e} }}}.}

El menor valor posible r en el átomo de hidrógenoZ = 1) se llama el radio Bohr y es igual a:

{displaystyle r_{1}={frac {hbar ^{2}}{k_{mathrm {e} }e^{2}m_{mathrm {e} }}}approx 5.29times 10^{-11}~mathrm {m}.}

La energía de la n- el nivel para cualquier átomo es determinado por el radio y el número cuántico:

{displaystyle E=-{frac {Zk_{mathrm {e} }e^{2}}{2r_{n}}}=-{frac {Z^{2}(k_{mathrm {e} }e^{2})^{2}m_{mathrm {e} }}{2hbar ^{2}n^{2}}}approx {frac {-13.6Z^{2}}{n^{2}}}~mathrm {eV}.}

Por lo tanto, un electrón en el nivel de energía más bajo del hidrógeno (n = 1) tiene aproximadamente 13,6 eV menos de energía que un electrón inmóvil infinitamente lejos de el núcleo. El siguiente nivel de energía (n = 2) es −3,4 eV. El tercero (n = 3) es −1,51 eV, y así sucesivamente. Para valores mayores de n, estas son también las energías de enlace de un átomo altamente excitado con un electrón en una gran órbita circular alrededor del resto del átomo. La fórmula del hidrógeno también coincide con el producto de Wallis.

La combinación de constantes naturales en la fórmula energética se denomina energía de Rydberg (R_E):

{displaystyle R_{mathrm {E} }={frac {(k_{mathrm {e} }e^{2})^{2}m_{mathrm {e} }}{2hbar ^{2}}}.}

Esta expresión se aclara interpretándola en combinaciones que forman unidades más naturales:

{displaystyle m_{mathrm {e} }c^{2}}

es la energía de masa restante del electrón (511 keV),

{displaystyle {frac {k_{mathrm {e} }e^{2}}{hbar c}}=alpha approx {frac {1}{137}}}

es la constante de la estructura fina,

{displaystyle R_{mathrm {E} }={frac {1}{2}}(m_{mathrm {e} }c^{2})alpha ^{2}}

Dado que esta derivación es con la suposición de que el núcleo está orbitado por un electrón, podemos generalizar este resultado dejando que el núcleo tenga una carga q = Ze, donde Z es el número atómico. Esto ahora nos dará los niveles de energía para los átomos hidrogenados (similares al hidrógeno), que pueden servir como una aproximación aproximada del orden de magnitud de los niveles de energía reales. Entonces, para núcleos con protones Z, los niveles de energía son (en una aproximación aproximada):

{displaystyle E_{n}=-{frac {Z^{2}R_{mathrm {E} }}{n^{2}}}.}

Los niveles de energía reales no se pueden resolver analíticamente para más de un electrón (consulte el problema de n cuerpos) porque los electrones no solo se ven afectados por el núcleo, sino que también interactúan entre sí a través de la fuerza de Coulomb.

Cuando Z = 1/α (Z ≈ 137), el movimiento se vuelve altamente relativista, y Z² cancela el α² en R; la energía de la órbita comienza a ser comparable a la energía en reposo. Los núcleos lo suficientemente grandes, si fueran estables, reducirían su carga creando un electrón ligado desde el vacío, expulsando el positrón al infinito. Este es el fenómeno teórico del apantallamiento de carga electromagnética que predice una carga nuclear máxima. Se ha observado la emisión de tales positrones en las colisiones de iones pesados para crear núcleos superpesados temporales.

La fórmula de Bohr utiliza correctamente la masa reducida del electrón y el protón en todas las situaciones, en lugar de la masa del electrón,

{displaystyle m_{text{red}}={frac {m_{mathrm {e} }m_{mathrm {p} }}{m_{mathrm {e} }+m_{mathrm {p} }}}=m_{mathrm {e} }{frac {1}{1+m_{mathrm {e} }/m_{mathrm {p} }}}.}

Sin embargo, estos números son casi iguales, debido a la masa mucho mayor del protón, alrededor de 1836,1 veces la masa del electrón, por lo que la masa reducida en el sistema es la masa del electrón multiplicada por la constante 1836,1/(1+1836,1) = 0,99946. Este hecho fue históricamente importante para convencer a Rutherford de la importancia del modelo de Bohr, ya que explicaba el hecho de que las frecuencias de las líneas en los espectros del helio ionizado solo no difieren de las del hidrógeno en un factor de exactamente 4, sino más bien por 4 veces la relación de la masa reducida para los sistemas de hidrógeno y helio, que estaba mucho más cerca de la relación experimental que exactamente 4.

Para el positronio, la fórmula también usa la masa reducida, pero en este caso, es exactamente la masa del electrón dividida por 2. Para cualquier valor del radio, el electrón y el positrón se mueven cada uno a la mitad de la velocidad alrededor de su centro común de masa, y cada uno tiene sólo un cuarto de la energía cinética. La energía cinética total es la mitad de lo que sería para un solo electrón que se mueve alrededor de un núcleo pesado.

{displaystyle E_{n}={frac {R_{mathrm {E} }}{2n^{2}}}}

(positronio).

Fórmula de Rydberg

La fórmula de Rydberg, que se conocía empíricamente antes que la fórmula de Bohr, se considera en la teoría de Bohr como una descripción de las energías de las transiciones o saltos cuánticos entre niveles de energía orbitales. La fórmula de Bohr da el valor numérico de la constante de Rydberg ya conocida y medida, pero en términos de constantes de la naturaleza más fundamentales, incluida la carga del electrón y la constante de Planck.

Cuando el electrón se mueve de su nivel de energía original a uno más alto, salta cada nivel hacia atrás hasta que llega a la posición original, lo que resulta en la emisión de un fotón. Utilizando la fórmula derivada para los diferentes niveles de energía del hidrógeno, se pueden determinar las longitudes de onda de la luz que puede emitir un átomo de hidrógeno.

La energía de un fotón emitido por un átomo de hidrógeno viene dada por la diferencia de dos niveles de energía del hidrógeno:

{displaystyle E=E_{i}-E_{f}=R_{text{E}}left({frac {1}{n_{f}^{2}}}-{frac {1}{n_{i}^{2}}}right),}

donde $n f$ es el nivel de energía final, y $n i$ es el nivel de energía inicial.

Dado que la energía de un fotón es

E={frac {hc}{lambda }},

la longitud de onda del fotón emitido viene dada por

{displaystyle {frac {1}{lambda }}=Rleft({frac {1}{n_{f}^{2}}}-{frac {1}{n_{i}^{2}}}right).}

Esto se conoce como la fórmula de Rydberg, y la constante de Rydberg $R$ es $R E / hc$ , o $R E / 2 π$ en unidades naturales. Esta fórmula era conocida en el siglo XIX por los científicos que estudiaban la espectroscopia, pero no había una explicación teórica para esta forma o una predicción teórica para el valor de $R$ , hasta Bohr. De hecho, la derivación de Bohr de la constante de Rydberg, así como la concordancia concomitante de la fórmula de Bohr con las líneas espectrales observadas experimentalmente de Lyman ( $n f$ =1), Balmer ( $n f$ =2) y Paschen ( $n f$ =3) series, y la predicción teórica exitosa de otras líneas aún no observadas, fue una de las razones por las que su modelo fue aceptado de inmediato.

Para aplicar a átomos con más de un electrón, la fórmula de Rydberg se puede modificar reemplazando $Z$ con $Z - b$ o $n$ con $n - b$ donde $b$ es una constante que representa un efecto de filtrado debido a la capa interna y a otros electrones (ver Capa de electrones y la discusión posterior del 'Modelo de capa del átomo' a continuación). Esto se estableció empíricamente antes de que Bohr presentara su modelo.

Modelo de caparazón (átomos más pesados)

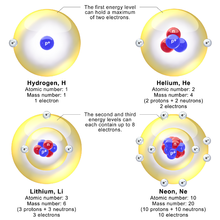
Los tres artículos originales de Bohr en 1913 describían principalmente la configuración electrónica en elementos más ligeros. Bohr llamó a sus capas de electrones "anillos" en 1913. Los orbitales atómicos dentro de las capas no existían en el momento de su modelo planetario. Bohr explica en la Parte 3 de su famoso artículo de 1913 que el máximo de electrones en una capa es de ocho, y escribe: “Vemos, además, que un anillo de n electrones no puede girar en un solo anillo alrededor de un núcleo. sin cargo n_e a menos que n < 8.” Para átomos más pequeños, las capas de electrones se llenarían de la siguiente manera: “los anillos de electrones solo se unirán si contienen el mismo número de electrones; y que, en consecuencia, el número de electrones en los anillos internos será solo de 2, 4, 8”. Sin embargo, en átomos más grandes, la capa más interna contendría ocho electrones, “por otro lado, el sistema periódico de los elementos sugiere fuertemente que ya en el neón N = 10 se producirá un anillo interno de ocho electrones”. Bohr escribió "De lo anterior nos lleva al siguiente esquema posible para la disposición de los electrones en los átomos ligeros:"

Las configuraciones propuestas por Bohr 1913
Elemento	Electrones por concha	Elemento	Electrones por concha	Elemento	Electrones por concha
1	1	9	4, 4, 1	17	8, 4, 4, 1
2	2	10	8, 2	18	8, 8, 2
3	2, 1	11	8, 2, 1	19	8, 8, 2, 1
4	2, 2	12	8, 2, 2	20	8, 8, 2, 2
5	2, 3	13	8, 2, 3	21	8, 8, 2, 3
6	2, 4	14	8, 2, 4	22	8, 8, 2, 4
7	4, 3	15	8, 4, 3	23	8, 8, 4, 3
8	4, 2, 2	16	8, 4, 2, 2	24	8, 8, 4, 2, 2

En el tercer artículo de Bohr de 1913, Parte III, llamado sistemas que contienen varios núcleos, dice que dos átomos forman moléculas en un plano simétrico y vuelve a describir el hidrógeno. El modelo de Bohr de 1913 no analizaba en detalle los elementos superiores y John William Nicholson fue uno de los primeros en demostrar en 1914 que no podía funcionar para el litio, pero era una teoría atractiva para el hidrógeno y el helio ionizado.

En 1921, siguiendo el trabajo de los químicos y otros involucrados en el trabajo sobre la tabla periódica, Bohr amplió el modelo del hidrógeno para dar un modelo aproximado para átomos más pesados. Esto dio una imagen física que reprodujo muchas propiedades atómicas conocidas por primera vez, aunque estas propiedades se propusieron simultáneamente con el trabajo idéntico del químico Charles Rugeley Bury.

El compañero de investigación de Bohr entre 1914 y 1916 fue Walther Kossel, quien corrigió el trabajo de Bohr para mostrar que los electrones interactuaban a través de los anillos exteriores, y Kossel llamó a los anillos: "capas". A Irving Langmuir se le atribuye la primera disposición viable de electrones en capas con solo dos en la primera capa y subiendo a ocho en la siguiente según la regla del octeto de 1904, aunque Kossel ya había predicho un máximo de ocho por capa en 1916. Los átomos más pesados tienen más protones en el núcleo y más electrones para cancelar la carga. Bohr tomó de estos químicos la idea de que cada órbita discreta solo podía contener una cierta cantidad de electrones. Según Kossel, después de que la órbita esté llena, se tendría que usar el siguiente nivel. Esto le da al átomo una estructura de capa diseñada por Kossel, Langmuir y Bury, en la que cada capa corresponde a una órbita de Bohr.

Este modelo es incluso más aproximado que el modelo del hidrógeno, porque trata a los electrones de cada capa como si no interactuaran. Pero las repulsiones de los electrones se tienen en cuenta de alguna manera por el fenómeno del apantallamiento. Los electrones en las órbitas exteriores no solo giran alrededor del núcleo, sino que también se mueven alrededor de los electrones interiores, por lo que la carga efectiva Z que sienten se reduce por el número de electrones en la órbita interior.

Por ejemplo, el átomo de litio tiene dos electrones en la órbita más baja de 1s, y estos orbitan en Z = 2. Cada uno ve la carga nuclear de Z = 3 menos el efecto de pantalla del otro, que reduce bruscamente la carga nuclear en 1 unidad. Esto significa que los electrones más internos orbitan aproximadamente a la mitad del radio de Bohr. El electrón más externo en el litio orbita aproximadamente en el radio de Bohr, ya que los dos electrones internos reducen la carga nuclear en 2. Este electrón externo debe estar a casi un radio de Bohr del núcleo. Debido a que los electrones se repelen fuertemente entre sí, la descripción de la carga efectiva es muy aproximada; el cargo efectivo Z generalmente no resulta ser un número entero. Pero la ley de Moseley prueba experimentalmente el par de electrones más interno y muestra que ven una carga nuclear de aproximadamente Z − 1, mientras que el electrón más externo en un átomo o ion con solo un electrón en la capa más externa orbita un núcleo con carga efectiva Z − k donde k es el número total de electrones en las capas internas.

El modelo de caparazón pudo explicar cualitativamente muchas de las misteriosas propiedades de los átomos que se codificaron a finales del siglo XIX en la tabla periódica de los elementos. Una propiedad era el tamaño de los átomos, que podía determinarse aproximadamente midiendo la viscosidad de los gases y la densidad de los sólidos cristalinos puros. Los átomos tienden a hacerse más pequeños hacia la derecha en la tabla periódica y se vuelven mucho más grandes en la siguiente línea de la tabla. Los átomos a la derecha de la tabla tienden a ganar electrones, mientras que los átomos a la izquierda tienden a perderlos. Cada elemento de la última columna de la tabla es químicamente inerte (gas noble).

En el modelo de caparazón, este fenómeno se explica por el relleno de caparazón. Los átomos sucesivos se vuelven más pequeños porque están llenando órbitas del mismo tamaño, hasta que la órbita está llena, momento en el que el siguiente átomo en la tabla tiene un electrón externo débilmente unido, lo que hace que se expanda. La primera órbita de Bohr se llena cuando tiene dos electrones, lo que explica por qué el helio es inerte. La segunda órbita permite ocho electrones, y cuando está llena el átomo es neón, nuevamente inerte. El tercer orbital contiene ocho nuevamente, excepto que en el tratamiento de Sommerfeld más correcto (reproducido en la mecánica cuántica moderna) hay "d" electrones La tercera órbita puede contener 10 electrones d adicionales, pero estas posiciones no se llenan hasta que se llenan algunos orbitales más del siguiente nivel (llenar los orbitales n = 3 d produce los 10 elementos de transición). El patrón de llenado irregular es un efecto de las interacciones entre electrones, que no se tienen en cuenta ni en los modelos de Bohr ni en los de Sommerfeld y que son difíciles de calcular incluso en el tratamiento moderno.

Ley y cálculo de Moseley (líneas de emisión de rayos X K-alfa)

Niels Bohr dijo en 1962: 'Ves, en realidad, el trabajo de Rutherford no se tomó en serio. No podemos entender hoy, pero no se tomó en serio en absoluto. No había mención de ello en ningún lugar. El gran cambio vino de Moseley."

En 1913, Henry Moseley encontró una relación empírica entre la línea de rayos X más fuerte emitida por los átomos bajo el bombardeo de electrones (entonces conocida como línea K-alfa) y su número atómico $Z$ . Se descubrió que la fórmula empírica de Moseley se derivaba de la fórmula de Rydberg y, más tarde, de la fórmula de Bohr (Moseley en realidad menciona solo a Ernest Rutherford y Antonius Van den Broek en términos de modelos, ya que se habían publicado antes que Moseley). El trabajo de #39 y el artículo de 1913 de Moseley se publicaron el mismo mes que el primer artículo modelo de Bohr). Las dos suposiciones adicionales de que [1] esta línea de rayos X proviene de una transición entre niveles de energía con números cuánticos 1 y 2, y [2], que el número atómico $Z$ cuando se usa en la fórmula para átomos más pesados que el hidrógeno, debe disminuirse en 1, a $(Z - 1) 2$ .

Moseley le escribió a Bohr, desconcertado por sus resultados, pero Bohr no pudo ayudar. En ese momento, pensó que el postulado "K" capa de electrones debería tener al menos cuatro electrones, no los dos que habrían explicado claramente el resultado. Entonces Moseley publicó sus resultados sin una explicación teórica.

Fue Walther Kossel en 1914 y en 1916 quien explicó que en la tabla periódica se crearían nuevos elementos a medida que se agregaran electrones a la capa externa. En el artículo de Kossel, escribe: “Esto lleva a la conclusión de que los electrones, que se agregan más, deben colocarse en anillos concéntricos o capas, en cada uno de los cuales... solo una cierta cantidad de electrones, a saber, ocho en nuestro caso, debe ser arreglado. Tan pronto como se completa un anillo o caparazón, se debe comenzar uno nuevo para el siguiente elemento; el número de electrones, que son más fácilmente accesibles y se encuentran en la periferia más externa, aumenta nuevamente de elemento a elemento y, por lo tanto, en la formación de cada nueva capa se repite la periodicidad química”. Más tarde, el químico Langmuir se dio cuenta de que el efecto era causado por la detección de carga, con una capa interna que contenía solo 2 electrones. En su artículo de 1919, Irving Langmuir postuló la existencia de "células" cada uno de los cuales solo podía contener dos electrones, y estos estaban dispuestos en "capas equidistantes".

En el experimento de Moseley, se elimina uno de los electrones más internos del átomo, lo que deja una vacante en la órbita de Bohr más baja, que contiene un único electrón restante. Luego, esta vacante se llena con un electrón de la siguiente órbita, que tiene n = 2. Pero los n=2 electrones ven una carga efectiva de Z − 1, que es el valor apropiado para la carga del núcleo, cuando un solo electrón permanece en la órbita de Bohr más baja para filtrar la carga nuclear + Z, y bájelo en −1 (debido a que la carga negativa del electrón oculta la carga nuclear positiva). La energía ganada por un electrón que cae de la segunda capa a la primera da la ley de Moseley para las líneas K-alfa,

{displaystyle E=hnu =E_{i}-E_{f}=R_{mathrm {E} }(Z-1)^{2}left({frac {1}{1^{2}}}-{frac {1}{2^{2}}}right),}

{displaystyle f=nu =R_{mathrm {v} }left({frac {3}{4}}right)(Z-1)^{2}=(2.46times 10^{15}~{text{Hz}})(Z-1)^{2}.}

Aquí, R_v = R_E/h es la constante de Rydberg, en términos de frecuencia igual a 3,28 x 10¹⁵ Hz. Para valores de Z entre 11 y 31, esta última relación había sido deducida empíricamente por Moseley, en un gráfico simple (lineal) de la raíz cuadrada de la frecuencia de rayos X contra el número atómico (sin embargo, para la plata, Z = 47, el obtenido experimentalmente el término de cribado debe sustituirse por 0,4). A pesar de su validez restringida, la ley de Moseley no solo estableció el significado objetivo del número atómico, sino que, como señaló Bohr, también hizo más que la derivación de Rydberg para establecer la validez del modelo nuclear de Rutherford/Van den Broek/Bohr. el átomo, con número atómico (lugar en la tabla periódica) representando unidades enteras de carga nuclear. Van den Broek había publicado su modelo en enero de 1913 mostrando que la tabla periódica estaba ordenada según la carga, mientras que el modelo atómico de Bohr no se publicó hasta julio de 1913.

Ahora se sabe que la línea K-alfa de la época de Moseley es un par de líneas cercanas, escritas como (Kα₁ y Kα ₂) en notación Siegbahn.

Deficiencias

El modelo de Bohr da un valor incorrecto $L = ħ$ para el momento angular orbital del estado fundamental: El momento angular en el estado fundamental verdadero se sabe que es cero a partir del experimento. Aunque las imágenes mentales fallan algo en estos niveles de escala, un electrón en el 'orbital' moderno más bajo sin momento orbital, se puede pensar que no gira 'alrededor' el núcleo en absoluto, sino simplemente para rodearlo con fuerza en una elipse con área cero (esto puede representarse como 'adelante y atrás', sin golpear o interactuar con el núcleo). Esto solo se reproduce en un tratamiento semiclásico más sofisticado como el de Sommerfeld. Aún así, incluso el modelo semiclásico más sofisticado no logra explicar el hecho de que el estado de energía más bajo es esféricamente simétrico: no apunta en ninguna dirección en particular.

Sin embargo, en el tratamiento totalmente cuántico moderno en el espacio de fases, la deformación adecuada (extensión completa cuidadosa) del resultado semiclásico ajusta el valor del momento angular al efectivo correcto. Como consecuencia, la expresión del estado fundamental físico se obtiene mediante un desplazamiento de la expresión del momento angular cuántico que se desvanece, que corresponde a la simetría esférica.

En la mecánica cuántica moderna, el electrón en el hidrógeno es una nube esférica de probabilidad que se vuelve más densa cerca del núcleo. La constante de tasa de probabilidad de decaimiento en el hidrógeno es igual a la inversa del radio de Bohr, pero dado que Bohr trabajó con órbitas circulares, no con elipses de área cero, el hecho de que estos dos números coincidan exactamente se considera una "coincidencia". 34;. (Sin embargo, se encuentran muchos acuerdos coincidentes de este tipo entre el tratamiento del átomo semiclásico frente al tratamiento mecánico cuántico completo; estos incluyen niveles de energía idénticos en el átomo de hidrógeno y la derivación de una constante de estructura fina, que surge del modelo relativista de Bohr-Sommerfeld. (ver más abajo) y que resulta ser igual a un concepto completamente diferente, en plena mecánica cuántica moderna).

El modelo de Bohr también tiene dificultades para explicar:

Gran parte del espectro de átomos más grandes. En el mejor de los casos, puede hacer predicciones sobre el K-alpha y algunos espectros de emisión de rayos X L-alpha para átomos más grandes, si dos. Se hacen nuevas hipótesis especiales. Los espectros de emisiones para átomos con un solo electrón externo (atomos en el grupo de litio) también se pueden predecir aproximadamente. Además, si se conocen los factores empíricos de detección de electrones nucleares para muchos átomos, muchas otras líneas espectrales pueden deducirse de la información, en átomos similares de elementos diferentes, a través de los principios combinados Ritz-Rydberg (ver fórmula Rydberg). Todas estas técnicas esencialmente hacen uso de la imagen potencial-energética de Bohr del átomo.
las intensidades relativas de líneas espectrales; aunque en algunos casos simples, la fórmula o modificaciones de Bohr, pudo proporcionar estimaciones razonables (por ejemplo, cálculos de Kramers para el efecto Stark).
La existencia de estructura fina y estructura hiperfinada en líneas espectrales, que se sabe que son debido a una variedad de efectos relativistas y sutiles, así como complicaciones de la columna electrones.
El efecto Zeeman – cambios en las líneas espectrales debido a campos magnéticos externos; estos también se deben a principios cuánticos más complicados que interactúan con el giro electrónico y los campos magnéticos orbitales.
El modelo también viola el principio de incertidumbre en que considera que los electrones tienen órbitas y lugares conocidos, dos cosas que no se pueden medir simultáneamente.
Los dobletes y trillizos aparecen en el espectro de algunos átomos como pares muy cercanos de líneas. El modelo de Bohr no puede decir por qué algunos niveles de energía deberían estar muy unidos.
Los átomos multielectrónicos no tienen niveles de energía predicho por el modelo. No funciona para el helio (neutral).

Refinamientos

Órbitas elípticas con la misma energía y impulso angular cuantificado

Se propusieron varias mejoras al modelo de Bohr, en particular los modelos de Sommerfeld o Bohr-Sommerfeld, que sugerían que los electrones viajaban en órbitas elípticas alrededor de un núcleo en lugar de las órbitas circulares del modelo de Bohr. Este modelo complementó la condición de momento angular cuantificado del modelo de Bohr con una condición de cuantificación radial adicional, la condición de cuantificación de Wilson-Sommerfeld

{displaystyle int _{0}^{T}p_{r},dq_{r}=nh,}

donde p_r es el momento radial conjugado canónicamente a la coordenada q, que es la posición radial, y T es un período orbital completo. La integral es la acción de las coordenadas del ángulo de acción. Esta condición, sugerida por el principio de correspondencia, es la única posible, ya que los números cuánticos son invariantes adiabáticos.

El modelo de Bohr-Sommerfeld era fundamentalmente inconsistente y condujo a muchas paradojas. El número cuántico magnético medía la inclinación del plano orbital en relación con el plano xy y solo podía tomar unos pocos valores discretos. Esto contradecía el hecho obvio de que un átomo podía girarse de un lado a otro en relación con las coordenadas sin restricción. La cuantización de Sommerfeld se puede realizar en diferentes coordenadas canónicas y, en ocasiones, da respuestas diferentes. La incorporación de correcciones de radiación fue difícil porque requería encontrar coordenadas de ángulo de acción para un sistema combinado de radiación/átomo, lo cual es difícil cuando se permite que escape la radiación. Toda la teoría no se extendía a los movimientos no integrables, lo que significaba que muchos sistemas no podían tratarse ni siquiera en principio. Al final, el modelo fue reemplazado por el moderno tratamiento de la mecánica cuántica del átomo de hidrógeno, que fue dado por primera vez por Wolfgang Pauli en 1925, utilizando la mecánica matricial de Heisenberg. La imagen actual del átomo de hidrógeno se basa en los orbitales atómicos de la mecánica ondulatoria, que Erwin Schrödinger desarrolló en 1926.

Sin embargo, esto no quiere decir que el modelo de Bohr-Sommerfeld no tuviera éxito. Los cálculos basados en el modelo de Bohr-Sommerfeld pudieron explicar con precisión una serie de efectos espectrales atómicos más complejos. Por ejemplo, hasta las perturbaciones de primer orden, el modelo de Bohr y la mecánica cuántica hacen las mismas predicciones para la división de la línea espectral en el efecto Stark. Sin embargo, en perturbaciones de orden superior, el modelo de Bohr y la mecánica cuántica difieren, y las mediciones del efecto Stark bajo intensidades de campo altas ayudaron a confirmar la corrección de la mecánica cuántica sobre el modelo de Bohr. La teoría predominante detrás de esta diferencia radica en las formas de los orbitales de los electrones, que varían según el estado de energía del electrón.

Las condiciones de cuantización de Bohr-Sommerfeld plantean interrogantes en las matemáticas modernas. La condición de cuantificación semiclásica consistente requiere un cierto tipo de estructura en el espacio de fase, lo que impone limitaciones topológicas a los tipos de variedades simplécticas que se pueden cuantificar. En particular, la forma simpléctica debería ser la forma de curvatura de una conexión de un haz de líneas hermíticas, lo que se denomina precuantización.

Bohr también actualizó su modelo en 1922, asumiendo que ciertos números de electrones (por ejemplo, 2, 8 y 18) corresponden a "capas cerradas" estables.

Modelo del enlace químico

Niels Bohr propuso un modelo del átomo y un modelo del enlace químico. Según su modelo para una molécula diatómica, los electrones de los átomos de la molécula forman un anillo giratorio cuyo plano es perpendicular al eje de la molécula y equidistante de los núcleos atómicos. El equilibrio dinámico del sistema molecular se logra mediante el equilibrio de fuerzas entre las fuerzas de atracción de los núcleos al plano del anillo de electrones y las fuerzas de repulsión mutua de los núcleos. El modelo de Bohr del enlace químico tuvo en cuenta la repulsión de Coulomb: los electrones en el anillo están a la máxima distancia entre sí.

Contenido relacionado

Más resultados...