Magnetorresistencia

Magnetorresistencia es la tendencia de un material (a menudo ferromagnético) a cambiar el valor de su resistencia eléctrica en un campo magnético aplicado externamente. Hay una variedad de efectos que pueden llamarse magnetorresistencia. Algunos ocurren en metales y semiconductores no magnéticos a granel, como la magnetorresistencia geométrica, las oscilaciones de Shubnikov-de Haas o la magnetorresistencia positiva común en los metales. Otros efectos ocurren en los metales magnéticos, como la magnetorresistencia negativa en los ferromagnetos o la magnetorresistencia anisotrópica (AMR). Finalmente, en sistemas multicomponente o multicapa (por ejemplo, uniones de túnel magnético), se puede observar magnetorresistencia gigante (GMR), magnetorresistencia de túnel (TMR), magnetorresistencia colosal (CMR) y magnetorresistencia extraordinaria (EMR).

El primer efecto magnetorresistivo fue descubierto en 1856 por William Thomson, más conocido como Lord Kelvin, pero no pudo reducir la resistencia eléctrica de nada en más del 5 %. Hoy en día, se conocen sistemas que incluyen semimetales y estructuras EMR de anillos concéntricos. En estos, un campo magnético puede ajustar la resistencia por órdenes de magnitud. Dado que diferentes mecanismos pueden alterar la resistencia, es útil considerar por separado las situaciones en las que depende directamente de un campo magnético (p. ej., magnetorresistencia geométrica y magnetorresistencia multibanda) y aquellas en las que lo hace indirectamente a través de la magnetización (p. ej., AMR y TMR).

Descubrimiento

William Thomson (Lord Kelvin) descubrió por primera vez la magnetorresistencia ordinaria en 1856. Experimentó con piezas de hierro y descubrió que la resistencia aumenta cuando la corriente está en la misma dirección que la fuerza magnética y disminuye cuando la corriente está a 90° a la fuerza magnetica Luego hizo el mismo experimento con el níquel y descubrió que se veía afectado de la misma manera pero la magnitud del efecto era mayor. Este efecto se conoce como magnetorresistencia anisotrópica (AMR).

Disco Corbino. Con el campo magnético apagado, una corriente radial fluye en el anulus de conducción debido a la batería conectada entre los bordes de conductividad (infinito). Cuando un campo magnético a lo largo del eje se enciende (B señala directamente fuera de la pantalla), la fuerza Lorentz conduce un componente circular de corriente, y la resistencia entre los bordes interiores y externos suben. Este aumento de resistencia debido al campo magnético se llama magnetoresistencia.

En 2007, Albert Fert y Peter Grünberg recibieron conjuntamente el Premio Nobel por el descubrimiento de la magnetorresistencia gigante.

Magnetorresistencia geométrica

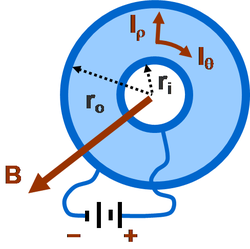
Un ejemplo de magnetorresistencia debida a la acción directa del campo magnético sobre la corriente eléctrica se puede estudiar en un disco de Corbino (ver figura). Consiste en un anillo conductor con bordes perfectamente conductores. Sin un campo magnético, la batería impulsa una corriente radial entre las llantas. Cuando se aplica un campo magnético perpendicular al plano del anillo (ya sea dentro o fuera de la página), también fluye una componente circular de corriente, debido a la fuerza de Lorentz. El interés inicial en este problema comenzó con Boltzmann en 1886 y Corbino lo revisó de forma independiente en 1911.

En un modelo simple, suponiendo que la respuesta a la fuerza de Lorentz es la misma que para un campo eléctrico, la velocidad de la portadora v viene dada por:

v=μ μ ()E+v× × B),{displaystyle mathbf {v} =muleft(mathbf {E} +mathbf {vtimes B} right)

donde μ es la movilidad del portador. Resolviendo para la velocidad, encontramos:

v=μ μ 1+()μ μ B)2()E+μ μ E× × B+μ μ 2()B⋅ ⋅ E)B)=μ μ 1+()μ μ B)2()E⊥ ⊥ +μ μ E× × B)+μ μ E∥ ∥ ,{displaystyle mathbf {v} ={frac {mu }{1+(mu B)^{2}}left(mathbf {E} +mu mathbf [Etimes B} +mu ^{2}(mathbf {Bcdot E})mathbf {B}right)={frac {mu }{1+(mu B)}}left(mathbf {E} _{perp }+mumathbf}

donde la reducción efectiva de la movilidad debida al campo B (para el movimiento perpendicular a este campo) es evidente. La corriente eléctrica (proporcional a la componente radial de la velocidad) disminuirá con el aumento del campo magnético y, por lo tanto, aumentará la resistencia del dispositivo. Críticamente, este escenario magnetorresistivo depende sensiblemente de la geometría del dispositivo y las líneas de corriente y no se basa en materiales magnéticos.

En un semiconductor con un solo tipo de portador, la magnetorresistencia es proporcional a (1 + (μB)²), donde μ es la movilidad del semiconductor (unidades m²·V⁻¹·s⁻¹ o T ⁻¹) y B es el campo magnético (unidades teslas). El antimoniuro de indio, un ejemplo de semiconductor de alta movilidad, podría tener una movilidad de electrones superior a 4 m²·V⁻¹·s⁻¹ en 300 K. Entonces, en un campo de 0.25 T, por ejemplo, el aumento de magnetorresistencia sería del 100%.

Magnetorresistencia anisotrópica (AMR)

La resistencia de una fina película Permalloy se muestra aquí como una función del ángulo de un campo externo aplicado.

Los experimentos de Thomson son un ejemplo de AMR, una propiedad de un material en la que se observa una dependencia de la resistencia eléctrica del ángulo entre la dirección de la corriente eléctrica y la dirección de la magnetización. El efecto surge de la acción simultánea de la magnetización y la interacción espín-órbita y su mecanismo detallado depende del material. Puede deberse, por ejemplo, a una mayor probabilidad de dispersión s-d de electrones en la dirección de magnetización (que está controlada por el campo magnético aplicado). El efecto neto (en la mayoría de los materiales) es que la resistencia eléctrica tiene un valor máximo cuando la dirección de la corriente es paralela al campo magnético aplicado. Se está investigando la RAM de nuevos materiales y se han observado magnitudes de hasta el 50 % en algunos compuestos de uranio ferromagnético.

En materiales ferromagnéticos policristalinos, el AMR sólo puede depender del ángulo φ φ =↑ ↑ − − Silencio Silencio {displaystyle varphi =psi -theta } entre la magnetización y la dirección actual y (si la resistencia del material puede ser descrita por un tensor de rango-dos), debe seguir

*** *** ()φ φ )=*** *** ⊥ ⊥ +()*** *** ∥ ∥ − − *** *** ⊥ ⊥ )#2⁡ ⁡ φ φ {displaystyle rho (varphi)=rho _{perp }+(rho _{parallel }-rho _{perp })cos ^{2}varphi }

Donde *** *** {displaystyle rho } es la resistencia (longitudinal) de la película y *** *** ∥ ∥ ,⊥ ⊥ {displaystyle rho _{parallelperp} son las resistencias para φ φ =0{displaystyle varphi =0} y 90∘ ∘ {displaystyle 90^{circ }}, respectivamente. Asociada con la resistividad longitudinal, también se abre la resistividad transversal (algo confuso[1]) el efecto plano Hall. En monocristalos, resistividad *** *** {displaystyle rho } depende también de ↑ ↑ ,Silencio Silencio {displaystyle psitheta} individualmente.

Para compensar las características no lineales y la incapacidad de detectar la polaridad de un campo magnético, se utiliza la siguiente estructura para los sensores. Consiste en tiras de aluminio u oro colocadas sobre una fina película de permalloy (un material ferromagnético que presenta el efecto AMR) inclinada en un ángulo de 45°. Esta estructura obliga a la corriente a no fluir a lo largo de los “ejes fáciles” de película delgada, sino en un ángulo de 45°. La dependencia de la resistencia ahora tiene un desplazamiento permanente que es lineal alrededor del punto nulo. Debido a su apariencia, este tipo de sensor se denomina 'barbero'.

El efecto AMR se utiliza en una amplia gama de sensores para la medición del campo magnético de la Tierra (brújula electrónica), para la medición de la corriente eléctrica (mediante la medición del campo magnético creado alrededor del conductor), para la detección del tráfico y para Detección de ángulo y posición lineal. Los mayores fabricantes de sensores AMR son Honeywell, NXP Semiconductors, STMicroelectronics y Sensitec GmbH.

Como aspectos teóricos, I. A. Campbell, A. Fert y O. Jaoul (CFJ) derivaron una expresión de la relación AMR para aleaciones basadas en Ni utilizando el modelo de dos corrientes con procesos de dispersión s-s y s-d, donde s es un electrón de conducción y d es estados 3d con la interacción espín-órbita. La relación AMR se expresa como

Δ Δ *** *** *** *** =*** *** ∥ ∥ − − *** *** ⊥ ⊥ *** *** ⊥ ⊥ =γ γ ()α α − − 1),{displaystyle {frac {Delta rho}{rho }={frac {rho _{parallel }-rho _{perp }{rho ################################################################################################################################################################################################################################################################ }=gamma (alpha -1),}

con γ γ =()3/4)()A/H)2{displaystyle gamma =(3/4)(A/H)^{2} y α α =*** *** ↓ ↓ /*** *** ↑ ↑ {displaystyle alpha =rho _{downarrow }/rho _{uparrow }, donde A{displaystyle A}, H{displaystyle H., y *** *** σ σ {displaystyle rho _{sigma } son una constante de acoplamiento de giro-orbito (llamado Especificaciones Especificaciones {displaystyle zeta }), un campo de intercambio, y una resistividad para el giro σ σ {displaystyle sigma }, respectivamente. Además, recientemente, Satoshi Kokado et al. han obtenido la expresión general de la relación AMR para ferromagnetes tridimensionales de transición al extender la teoría CFJ a uno más general. La expresión general también se puede aplicar a mediometales.