Longitud geográfica

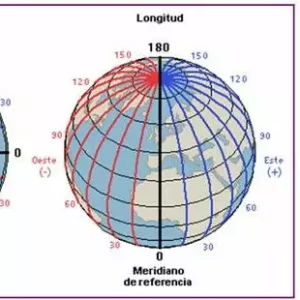
La Longitud geográfica es una coordenada en un sistema de referencia este—oeste de un punto en la superficie de la Tierra o de otro cuerpo celeste. Esta coordenada permite ubicar elementos en el sistema de referencia. La longitud se expresa en grados angulares y se representa utilizando la letra griega lambda (λ).

Por convención, se considera que la longitud es positiva hacia el este del meridiano de Greenwich y negativa hacia el oeste. Esta convención permite una localización precisa y uniforme en mapas y sistemas de navegación global.

Los meridianos —líneas imaginarias que se extienden de polo a polo— son también parte del sistema de referencia de la longitud geográfica; ya que, todos los puntos que a lo largo de un meridiano comparten la misma longitud. El meridiano de Greenwich, situado en el Observatorio Real cerca de Londres, Inglaterra, es el punto de partida de este sistema de medición, establecido como posición 0° de longitud.

Debido a la rotación de la Tierra, existe una estrecha relación entre la longitud geográfica y el tiempo. La hora local, que puede determinarse por la posición del Sol, cambia en función de la longitud: una variación de 15° en longitud equivale a una hora de diferencia en la hora local. Este fenómeno es la base para calcular la longitud a partir de la comparación entre la hora local y un estándar de tiempo absoluto.

Históricamente, la determinación del tiempo absoluto ha evolucionado: se ha podido obtener mediante la observación de eventos celestes, como eclipses lunares, visibles desde diferentes longitudes, o mediante la recepción de señales de tiempo sincronizadas por medios como el telégrafo o la radio.

Aunque el concepto es relativamente simple, el desarrollo de un método preciso y fiable para calcular la longitud fue una tarea compleja que se extendió a lo largo de los siglos. Este desafío capturó el ingenio y la dedicación de algunas de las más brillantes mentes científicas de la historia.

La longitud se establece generalmente a partir de la normal geodésica, que es la dirección de la gravedad en un lugar específico. Por otro lado, la latitud es la coordenada que define la posición norte-sur de un punto sobre la Tierra y se calcula como el ángulo entre la vertical en ese punto y el plano ecuatorial.

Es importante distinguir entre la longitud geográfica ordinaria y la longitud astronómica. La longitud astronómica puede presentar ligeras diferencias con respecto a la geográfica ordinaria debido a la desviación vertical, que son las pequeñas variaciones en el campo gravitatorio de la Tierra. Estas variaciones también afectan a la latitud astronómica, que es el ángulo entre la vertical real en un punto determinado y el plano ecuatorial.

Ambos tipos de longitud, la geográfica y la astronómica, son fundamentales en campos como la geodesia, la navegación y la astronomía, permitiendo una comprensión más profunda de la forma y la gravedad de nuestro planeta.

HSD

Historia

El concepto de longitud fue desarrollado por primera vez por los antiguos astrónomos griegos. Hiparco (siglo II a. C.) usó un sistema de coordenadas que asumía una Tierra esférica y la dividió en 360° como todavía lo hacemos hoy. Su meridiano principal pasaba por Alejandría. También propuso un método para determinar la longitud comparando la hora local de un eclipse lunar en dos lugares diferentes, demostrando así una comprensión de la relación entre la longitud y la hora. .Claudio Ptolomeo (siglo II d. C.) desarrolló un sistema de mapeo utilizando paralelos curvos que reducían la distorsión. También recopiló datos de muchos lugares, desde Gran Bretaña hasta el Medio Oriente. Usó un meridiano principal a través de las Islas Canarias, de modo que todos los valores de longitud serían positivos. Si bien el sistema de Ptolomeo era sólido, los datos que utilizó a menudo eran deficientes, lo que llevó a una gran sobreestimación (en aproximadamente un 70%) de la longitud del Mediterráneo.

Después de la caída del Imperio Romano, el interés por la geografía disminuyó considerablemente en Europa. Los astrónomos hindúes y musulmanes continuaron desarrollando estas ideas, agregando muchas ubicaciones nuevas y, a menudo, mejorando los datos de Ptolomeo. Por ejemplo, al-Battānī utilizó observaciones simultáneas de dos eclipses lunares para determinar la diferencia de longitud entre Antakya y Raqqa con un error de menos de 1°. Se considera que esto es lo mejor que se puede lograr con los métodos disponibles en ese momento: observación del eclipse a simple vista y determinación de la hora local utilizando un astrolabio para medir la altitud de una "estrella de reloj" adecuada.

A finales de la Edad Media, el interés por la geografía revivió en Occidente, a medida que aumentaban los viajes y la erudición árabe comenzó a conocerse a través del contacto con España y el norte de África. En el siglo XII se prepararon tablas astronómicas para varias ciudades europeas, basadas en el trabajo de al-Zarqālī en Toledo. El eclipse lunar del 12 de septiembre de 1178 se utilizó para establecer las diferencias de longitud entre Toledo, Marsella y Hereford.

Cristóbal Colón hizo dos intentos de utilizar los eclipses lunares para descubrir su longitud, el primero en la isla Saona, el 14 de septiembre de 1494 (segundo viaje), y el segundo en Jamaica el 29 de febrero de 1504 (cuarto viaje). Se supone que usó tablas astronómicas como referencia. Sus determinaciones de longitud mostraron grandes errores de 13° y 38° W respectivamente. Randles (1985) documenta la medición de la longitud por parte de portugueses y españoles entre 1514 y 1627 tanto en América como en Asia. Los errores oscilaron entre 2° y 25°.

El telescopio fue inventado a principios del siglo XVII. Inicialmente un dispositivo de observación, los desarrollos durante el siguiente medio siglo lo transformaron en una herramienta de medición precisa. El reloj de péndulo fue patentado por Christiaan Huygens en 1657 y aumentó la precisión unas 30 veces con respecto a los relojes mecánicos anteriores. Estos dos inventos revolucionarían la astronomía y la cartografía observacional.

En tierra, el período desde el desarrollo de telescopios y relojes de péndulo hasta mediados del siglo XVIII vio un aumento constante en el número de lugares cuya longitud se había determinado con una precisión razonable, a menudo con errores de menos de un grado, y casi siempre dentro de 2° a 3°. En la década de 1720, los errores eran consistentemente inferiores a 1°. En el mar durante el mismo período, la situación era muy diferente. Dos problemas resultaron intratables. El primero fue la necesidad de un navegador para obtener resultados inmediatos. El segundo fue el medio marino. Hacer observaciones precisas en un oleaje oceánico es mucho más difícil que en tierra, y los relojes de péndulo no funcionan bien en estas condiciones.

El cronómetro

En respuesta a los problemas de navegación, varias potencias marítimas europeas ofrecieron premios por un método para determinar la longitud en el mar. La más conocida de ellas es la Ley de Longitud aprobada por el parlamento británico en 1714. Ofrecía dos niveles de recompensas, para soluciones dentro de 1° y 0,5°. Se otorgaron recompensas por dos soluciones: distancias lunares, practicables gracias a las tablas de Tobias Mayer desarrolladas en un almanaque náutico por el astrónomo Royal Nevil Maskelyne; y para los cronómetros desarrollados por el carpintero y relojero de Yorkshire John Harrison. Harrison construyó cinco cronómetros durante más de tres décadas. Este trabajo fue apoyado y recompensado con miles de libras de la Junta de Longitud,pero luchó para recibir dinero hasta la recompensa máxima de £ 20,000, y finalmente recibió un pago adicional en 1773 después de la intervención del parlamento . Pasó algún tiempo antes de que cualquiera de los métodos se usara ampliamente en la navegación. En los primeros años, los cronómetros eran muy costosos y los cálculos requeridos para las distancias lunares aún eran complejos y requerían mucho tiempo. Las distancias lunares se generalizaron después de 1790. Los cronómetros tenían la ventaja de que tanto las observaciones como los cálculos eran más simples y, a medida que se abarataron a principios del siglo XIX, comenzaron a reemplazar a los lunares, que rara vez se usaban después de 1850.

Los primeros telégrafos en funcionamiento fueron establecidos en Gran Bretaña por Wheatstone y Cooke en 1839, y en los EE. UU. por Morse en 1844. Rápidamente se descubrió que el telégrafo podía usarse para transmitir una señal de tiempo para determinar la longitud. El método pronto se puso en uso práctico para la determinación de la longitud, especialmente en América del Norte, y en distancias cada vez más largas a medida que se expandía la red de telégrafos, incluida Europa occidental con la finalización de los cables transatlánticos. El US Coast Survey fue particularmente activo en este desarrollo, y no solo en los Estados Unidos. El Survey estableció cadenas de ubicaciones mapeadas a través de América Central y del Sur, las Indias Occidentales y hasta Japón y China en los años 1874-1890. Esto contribuyó en gran medida al mapeo preciso de estas áreas.

Si bien los navegantes se beneficiaron de las cartas precisas, no podían recibir señales de telégrafo mientras navegaban y, por lo tanto, no podían usar el método para navegar. Esto cambió cuando la telegrafía inalámbrica (radio) estuvo disponible a principios del siglo XX. Las señales horarias inalámbricas para el uso de los barcos se transmitieron desde Halifax, Nueva Escocia, a partir de 1907 y desde la Torre Eiffel en París desde 1910. Estas señales permitieron a los navegantes verificar y ajustar sus cronómetros con frecuencia.

Los sistemas de navegación por radio se generalizaron después de la Segunda Guerra Mundial. Todos los sistemas dependían de transmisiones de balizas de navegación fijas. Un receptor a bordo del barco calculó la posición del barco a partir de estas transmisiones. Permitieron una navegación precisa cuando la mala visibilidad impidió las observaciones astronómicas y se convirtieron en el método establecido para el envío comercial hasta que fue reemplazado por GPS a principios de la década de 1990.

Determinación

Los principales métodos para determinar la longitud se enumeran a continuación. Con una excepción (la declinación magnética), todos dependen de un principio común, que era determinar un tiempo absoluto a partir de un evento o medida y comparar el tiempo local correspondiente en dos lugares diferentes.

• Distancias lunares. En su órbita alrededor de la Tierra, la Luna se mueve en relación con las estrellas a una velocidad de poco más de 0,5°/hora. El ángulo entre la Luna y una estrella adecuada se mide con un sextante y (después de consultar tablas y largos cálculos) da un valor de tiempo absoluto.
• Satélites de Júpiter. Galileo propuso que con un conocimiento suficientemente preciso de las órbitas de los satélites, sus posiciones podrían proporcionar una medida del tiempo absoluto. El método requiere un telescopio, ya que las lunas no son visibles a simple vista.
• Apulsos, ocultaciones y eclipses. Un pulso es la distancia mínima aparente entre dos objetos (la Luna, una estrella o un planeta); una ocultación ocurre cuando una estrella o un planeta pasa detrás de la Luna, esencialmente un tipo de eclipse. Se siguieron utilizando los eclipses lunares. Los tiempos de cualquiera de estos eventos se pueden usar como la medida del tiempo absoluto.
• Cronómetros. Un reloj se ajusta a la hora local de un punto de partida cuya longitud se conoce, y la longitud de cualquier otro lugar se puede determinar comparando su hora local con la hora del reloj.
• Declinación magnética. En general, la aguja de una brújula no apunta exactamente al norte. La variación del norte verdadero varía según la ubicación, y se sugirió que esto podría proporcionar una base para la determinación de la longitud.

Con la excepción de la declinación magnética, todos demostraron ser métodos practicables. Los desarrollos en tierra y mar, sin embargo, fueron muy diferentes.

No hay otro principio físico que determine la longitud directamente sino con el tiempo. La longitud en un punto se puede determinar calculando la diferencia horaria entre la de su ubicación y la hora universal coordinada (UTC). Como hay 24 horas en un día y 360 grados en un círculo, el sol se mueve por el cielo a una velocidad de 15 grados por hora (360° ÷ 24 horas = 15° por hora). Entonces, si la zona horaria de una ubicación está tres horas por delante de UTC, entonces esa ubicación está cerca de los 45° de longitud (3 horas × 15° por hora = 45°). La palabra cercase usa porque el punto podría no estar en el centro de la zona horaria; además, las zonas horarias se definen políticamente, por lo que sus centros y límites a menudo no se encuentran en meridianos en múltiplos de 15°. Sin embargo, para realizar este cálculo, se necesita un cronómetro (reloj) configurado en UTC y se necesita determinar la hora local mediante observación solar o astronómica. Los detalles son más complejos de lo que se describe aquí: consulte los artículos sobre el tiempo universal y sobre la ecuación del tiempo para obtener más detalles.

Valores

La longitud se da como una medida angular que va desde 0° en el primer meridiano hasta +180° hacia el este y −180° hacia el oeste. La letra griega λ (lambda) se usa para indicar la ubicación de un lugar en la Tierra al este o al oeste del Primer Meridiano.

Cada grado de longitud se subdivide en 60 minutos, cada uno de los cuales se divide en 60 segundos. Por lo tanto, una longitud se especifica en notación sexagesimal como, por ejemplo, 23° 27′ 30″ E. Para mayor precisión, los segundos se especifican con una fracción decimal. Una representación alternativa utiliza grados y minutos, y las partes de un minuto se expresan en notación decimal, así: 23° 27,5′ E. Los grados también se pueden expresar como una fracción decimal: 23,45833° E. Para los cálculos, la medida angular se puede convertir a radianes, por lo que la longitud también se puede expresar de esta manera como una fracción con signo de π (pi), o una fracción sin signo de 2 π .

Para los cálculos, el sufijo Oeste/Este se reemplaza por un signo negativo en el hemisferio occidental. La convención estándar internacional (ISO 6709), que Este es positivo, es consistente con un sistema de coordenadas cartesianas de mano derecha, con el Polo Norte hacia arriba. Luego, una longitud específica puede combinarse con una latitud específica (positiva en el hemisferio norte) para dar una posición precisa en la superficie de la Tierra. De manera confusa, la convención de negativo para Oriente también se ve a veces, más comúnmente en los Estados Unidos; el Laboratorio de Investigación del Sistema Terrestre lo usó en una versión anterior de una de sus páginas, para "hacer que la entrada de coordenadas sea menos incómoda" para aplicaciones confinadas al hemisferio occidental. Desde entonces, han cambiado al enfoque estándar.

Tenga en cuenta que la longitud es singular en los polos y los cálculos que son lo suficientemente precisos para otras posiciones pueden ser inexactos en los polos o cerca de ellos. Además, la discontinuidad en el meridiano de ±180° debe manejarse con cuidado en los cálculos. Un ejemplo es un cálculo del desplazamiento hacia el este restando dos longitudes, lo que da una respuesta incorrecta si las dos posiciones están a ambos lados de este meridiano. Para evitar estas complejidades, considere reemplazar la latitud y la longitud con otra representación de posición horizontal en el cálculo.

Longitud de un grado de longitud

La longitud de un grado de longitud (distancia este-oeste) depende únicamente del radio de un círculo de latitud. Para una esfera de radio a, ese radio en la latitud φ es un cos φ , y la longitud de un grado (oπ/180radián) arco a lo largo de un círculo de latitud es{\displaystyle \Delta _{\rm {largo}}^{1}={\frac {\pi }{180}}a\cos \phi }

φ	Δ lat	Δ largo
0°	110.574 kilometros	111.320 kilometros
15°	110.649 kilometros	107.551 kilometros
30°	110.852 kilometros	96.486 kilometros
45°	111,133 kilometros	78.847 kilometros
60°	111.412 kilometros	55.800 kilometros
75°	111.618 kilometros	28,902 kilometros
90°	111.694 kilometros	0.000 kilometros

Cuando la Tierra es modelada por un elipsoide, esta longitud de arco se convierte en{\displaystyle \Delta_{\rm {largo}}^{1}={\frac {\pi a\cos \phi }{180{\sqrt {1-e^{2}\sin ^{2}\ fi }}}}}

donde e , la excentricidad del elipsoide, está relacionada con los ejes mayor y menor (los radios ecuatorial y polar respectivamente) por{\displaystyle e^{2}={\frac {a^{2}-b^{2}}{a^{2}}}}

Una fórmula alternativa es{\displaystyle \Delta _{\rm {long}}^{1}={\frac {\pi }{180}}a\cos \beta \quad {\mbox{donde}}\tan \beta ={\ fracción {b}{a}}\tan\phi}; aquí{\ estilo de visualización \ beta}es la llamada latitud paramétrica o reducida .

cos φ disminuye de 1 en el ecuador a 0 en los polos, lo que mide cómo los círculos de latitud se contraen desde el ecuador hasta un punto en el polo, por lo que la longitud de un grado de longitud también disminuye. Esto contrasta con el pequeño aumento (1%) en la longitud de un grado de latitud (distancia norte-sur), ecuador a polo. La tabla muestra ambos para el elipsoide WGS84 con a =6 378 137 .0 m y b =6 356 752 .3142 m . Tenga en cuenta que la distancia entre dos puntos separados por 1 grado en el mismo círculo de latitud, medida a lo largo de ese círculo de latitud, es ligeramente mayor que la distancia más corta (geodésica) entre esos puntos (a menos que estén en el ecuador, donde son iguales); la diferencia es inferior a 0,6 m (2 pies).

Una milla geográfica se define como la longitud de un minuto de arco a lo largo del ecuador (un minuto ecuatorial de longitud), por lo tanto, un grado de longitud a lo largo del ecuador es exactamente 60 millas geográficas o 111,3 kilómetros, ya que hay 60 minutos en un grado. La longitud de 1 minuto de longitud a lo largo del ecuador es 1 milla geográfica o 1,855 km o 1,153 millas, mientras que la longitud de 1 segundo es 0,016 milla geográfica o 30,916 mo ​​101,43 pies.