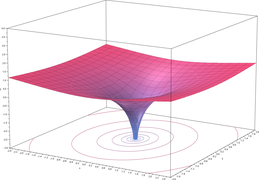
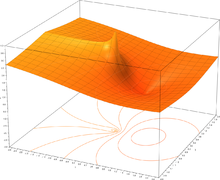
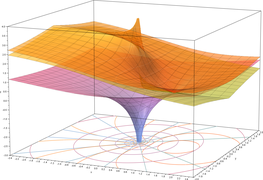
Logaritmo natural

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Logaritmo a la base de la constante matemática e

El logaritmo natural de un número es su logaritmo en la base de la constante matemática $e$ , que es un número irracional y trascendental aproximadamente igual a $2,718 281828 459. El logaritmo natural de x generalmente se escribe como ln x, log e x, o a veces, si la base e está implícito, simplemente log x . A veces se agregan paréntesis para mayor claridad, dando ln(x), log e (x), o log(x) . Esto se hace particularmente cuando el argumento del logaritmo no es un solo símbolo, para evitar ambigüedades.$

El logaritmo natural de $x$ es la potencia a la que $e$ tendría que elevarse para que sea igual a $x$ . Por ejemplo, $ln 7.5$ es $2.0149...$ , porque $e 2.0149... = 7.5$ . El logaritmo natural de $e$ mismo, $ln e$ , es $1$ , porque $e 1 = e$ , mientras que el logaritmo natural de $1$ es $0$ , ya que $e 0 = 1$ .

El logaritmo natural se puede definir para cualquier número real positivo $a$ como el área bajo la curva $y = 1/ x$ de $1$ a $a$ (con el área negativa cuando $0 < a < 1$ ). La simplicidad de esta definición, que coincide con muchas otras fórmulas que involucran el logaritmo natural, conduce al término "natural". La definición del logaritmo natural se puede ampliar para dar valores de logaritmo para números negativos y para todos los números complejos distintos de cero, aunque esto conduce a una función de varios valores: consulte Logaritmo complejo para obtener más información.

La función de logaritmo natural, si se considera como una función de valor real de una variable real positiva, es la función inversa de la función exponencial, lo que lleva a las identidades:

{displaystyle {begin{aligned}e^{ln x}&=xqquad {text{ if }}x{text{ is strictly positive,}}\ln e^{x}&=xqquad {text{ if }}x{text{ is any real number.}}end{aligned}}}

Como todos los logaritmos, el logaritmo natural convierte la multiplicación de números positivos en suma:

{displaystyle ln(xcdot y)=ln x+ln y~.}

Los logaritmos se pueden definir para cualquier base positiva que no sea 1, no sólo $e$ . Sin embargo, los logaritmos en otras bases difieren sólo por un multiplicador constante del logaritmo natural, y se puede definir en términos de este último, ${displaystyle log _{b}x=ln x/ln b=ln xcdot log _{b}e}$ .

Los logaritmos son útiles para resolver ecuaciones en las que la incógnita aparece como el exponente de alguna otra cantidad. Por ejemplo, los logaritmos se utilizan para resolver la vida media, la constante de decaimiento o el tiempo desconocido en problemas de decaimiento exponencial. Son importantes en muchas ramas de las matemáticas y las disciplinas científicas, y se utilizan para resolver problemas de interés compuesto.

Historia

El concepto de logaritmo natural fue desarrollado por Gregoire de Saint-Vincent y Alphonse Antonio de Sarasa antes de 1649. Su trabajo involucró la cuadratura de la hipérbola con ecuación $xy = 1$ , por determinación del área de sectores hiperbólicos. Su solución generó el "logaritmo hiperbólico" función, que tenía las propiedades ahora asociadas con el logaritmo natural.

Una primera mención del logaritmo natural la hizo Nicholas Mercator en su obra Logarithmotechnia, publicada en 1668, aunque el profesor de matemáticas John Speidell ya había compilado una tabla de lo que en realidad eran logaritmos naturales en 1619. Se ha dicho que los logaritmos de Speidell estaban en la base $e$ , pero esto no es del todo cierto debido a complicaciones con los valores que se expresan como números enteros.

Convenciones de notación

Las notaciones $ln x$ y $log e x$ ambos se refieren inequívocamente al logaritmo natural de $x$ , y $log x$ sin una base explícita también puede referirse al logaritmo natural. Este uso es común en matemáticas, junto con algunos contextos científicos, así como en muchos lenguajes de programación. Sin embargo, en algunos otros contextos, como la química, $log x$ se puede usar para denotar el logaritmo común (base 10). También puede referirse al logaritmo binario (base 2) en el contexto de la informática, particularmente en el contexto de la complejidad del tiempo.

Definiciones

El logaritmo natural se puede definir de varias formas equivalentes.

Inverso de exponencial

La definición más general es como la función inversa de $e^{x}$ Así que ${displaystyle e^{ln(x)}=x}$ . Porque... $e^{x}$ es positivo e invertible para cualquier entrada real $x$ , esta definición de $ln(x)$ está bien definido para cualquier positivo x. Para los números complejos, $e^{z}$ no es invertible, así que $ln(z)$ es una función multivalorada. Para hacer $ln(z)$ una función adecuada y única, por lo tanto, necesitamos restringirla a una rama principal particular, a menudo denotada por ${displaystyle operatorname {Ln} (z)}$ . Como la función inversa $e^{z}$ , $ln(z)$ puede definirse invirtiendo la definición habitual de $e^{z}$ :

{displaystyle e^{z}=lim _{nto infty }left(1+{frac {z}{n}}right)^{n}}

Hacerlo produce:

{displaystyle ln(z)=lim _{nto infty }ncdot ({sqrt[{n}]{z}}-1)}

Esta definición, por lo tanto, deriva su propia rama principal de la rama principal de las raíces enésimas.

Definición integral

In a

como el área de la región sombreada bajo la curva

f () x) = 1/ x

desde

1

a

. Si

a

es menos que

1

, la zona tomada como negativa.

El área bajo la hiperbola satisface la regla del logaritmo. Aquí.

A () s, t)

denota la zona bajo la hiperbola entre

s

t

El logaritmo natural de un número real positivo $a$ puede definirse como el área bajo el gráfico de la hipérbola con ecuación $y = 1/ x$ entre $x = 1$ y $x = a$ . esta es la integral

{displaystyle ln a=int _{1}^{a}{frac {1}{x}},dx.}

Si $a$ es menor que $1$ , esta área se considera ser negativo.

Esta función es un logaritmo porque satisface la propiedad multiplicativa fundamental de un logaritmo:

{displaystyle ln(ab)=ln a+ln b.}

Esto se puede demostrar dividiendo la integral que define $ln ab$ en dos partes y luego haciendo la sustitución variable $x = en$ (entonces $dx = a dt$ ) en la segunda parte, de la siguiente manera:

{displaystyle {begin{aligned}ln ab=int _{1}^{ab}{frac {1}{x}},dx&=int _{1}^{a}{frac {1}{x}},dx+int _{a}^{ab}{frac {1}{x}},dx\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{at}}a,dt\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{t}},dt\[5pt]&=ln a+ln b.end{aligned}}}

En términos elementales, esto es simplemente escalar por $1/ a$ en la dirección horizontal y por $a$ en dirección vertical. El área no cambia bajo esta transformación, pero la región entre $a$ y $ab$ se reconfigura. Porque la función $a /(ax)$ es igual a la función $1/ x$ , el área resultante es precisamente $ln b$ .

El número $e$ se puede definir como el número real único $a$ tal que $ln a = 1$ .

El logaritmo natural también tiene una representación integral impropia, que se puede derivar con el teorema de Fubini de la siguiente manera:

${displaystyle ln left(xright)=int _{1}^{x}{frac {1}{u}}du=int _{1}^{x}int _{0}^{infty }e^{-tu} dt du=int _{0}^{infty }int _{1}^{x}e^{-tu} du dt=int _{0}^{infty }{frac {e^{-t}-e^{-tx}}{t}}dt}$

Propiedades

${displaystyle ln 1=0}$
${displaystyle ln e=1}$
$0;{text{and }};y>0}" xmlns="http://www.w3.org/1998/Math/MathML">In⁡ ⁡ ()xSí.)=In⁡ ⁡ x+In⁡ ⁡ Sí.parax■0ySí.■0{displaystyle ln(xy)=ln x+ln yquad {text{for ################################################################################################################################################################################################################################################################ - Sí.0;{text{and }};y>0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fadc8b5815591a884a92b90f72dc571da3a8db37" style="vertical-align: -0.838ex; width:42.271ex; height:2.843ex;"/>$
${displaystyle ln(x/y)=ln x-ln y}$
$0}" xmlns="http://www.w3.org/1998/Math/MathML">In⁡ ⁡ ()xSí.)=Sí.In⁡ ⁡ xparax■0{displaystyle ln(x^{y})=yln xquad {text{for };x {0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/525c7cfa5c3779af39c5f1ad063c7f1fef366490" style="vertical-align: -0.838ex; width:26.35ex; height:2.843ex;"/>$
$<math alttext="{displaystyle ln x<ln yquad {text{for }};0<xIn x.In Sí.para0.x.Sí.{displaystyle ln x wonln yquad {text{for };0cantado <img alt="{displaystyle ln x<ln yquad {text{for }};0<x$
$lim _{{xto 0}}{frac {ln(1+x)}{x}}=1$
$0}" xmlns="http://www.w3.org/1998/Math/MathML">limα α → → 0xα α − − 1α α =In⁡ ⁡ xparax■0{displaystyle lim _{alpha to 0}{frac {x^{alpha }-1}{alpha }=ln xquad {text{for };x}0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ffdf20e3bd949f7095ade82873d87fdfbf5150dc" style="vertical-align: -2.005ex; width:30.037ex; height:5.343ex;"/>$
$0}" xmlns="http://www.w3.org/1998/Math/MathML">x− − 1x≤ ≤ In⁡ ⁡ x≤ ≤ x− − 1parax■0{displaystyle {frac {x-1}{x}}leq ln xleq x-1quad {text{for}quad x título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7cd8d97775e47c1771dc9ddddf7d14107f07045b" style="vertical-align: -1.838ex; width:34.376ex; height:5.176ex;"/>$
${displaystyle ln {(1+x^{alpha })}leq alpha xquad {text{for}}quad xgeq 0;{text{and }};alpha geq 1}$

Prueba
La declaración es verdadera $x=0$ , y ahora mostramos que $frac{d}{dx} ln{(1+x^alpha)} leq frac{d}{dx} (alpha x)$ para todos $x$ , que completa la prueba por el teorema fundamental del cálculo. Por lo tanto, queremos mostrar que $frac{d}{dx} ln{(1+x^alpha)} = frac{alpha x^{alpha - 1}}{1 + x^alpha} leq alpha = frac{d}{dx} (alpha x)$ (Nota que todavía no hemos probado que esta declaración es verdadera.) Si esto es cierto, entonces multiplicando la declaración media por la cantidad positiva $(1+x^alpha) / alpha$ y subcontratación $x^{alpha }$ obtendremos $x^{alpha-1} leq x^alpha + 1$ $x^{alpha-1} (1-x) leq 1$ Esta declaración es trivialmente verdadera para $xgeq 1$ ya que el lado izquierdo es negativo o cero. Para $<math alttext="{displaystyle 0leq x0\leq \leq x.1{displaystyle 0leq x 0} <img alt="0 le x$ todavía es cierto ya que ambos factores en la izquierda son menos de 1 (recuerdan que $alpha ge 1$ ). Así, esta última declaración es verdadera y repitiendo nuestros pasos en orden inverso encontramos que $frac{d}{dx} ln{(1+x^alpha)} leq frac{d}{dx} (alpha x)$ para todos $x$ . Esto completa la prueba. Una prueba alternativa es observar que ${displaystyle (1+x^{alpha })leq (1+x)^{alpha }}$ en las condiciones dadas. Esto puede probarse, por ejemplo, por las desigualdades de la norma. Tomando logaritmos y utilizando ${displaystyle ln(1+x)leq x}$ completa la prueba.

Prueba

La declaración es verdadera $x=0$ , y ahora mostramos que $frac{d}{dx} ln{(1+x^alpha)} leq frac{d}{dx} (alpha x)$ para todos $x$ , que completa la prueba por el teorema fundamental del cálculo. Por lo tanto, queremos mostrar que

frac{d}{dx} ln{(1+x^alpha)} = frac{alpha x^{alpha - 1}}{1 + x^alpha} leq alpha = frac{d}{dx} (alpha x)

(Nota que todavía no hemos probado que esta declaración es verdadera.) Si esto es cierto, entonces multiplicando la declaración media por la cantidad positiva $(1+x^alpha) / alpha$ y subcontratación $x^{alpha }$ obtendremos

x^{alpha-1} leq x^alpha + 1

x^{alpha-1} (1-x) leq 1

Esta declaración es trivialmente verdadera para $xgeq 1$ ya que el lado izquierdo es negativo o cero. Para $<math alttext="{displaystyle 0leq x0\leq \leq x.1{displaystyle 0leq x 0} <img alt="0 le x$ todavía es cierto ya que ambos factores en la izquierda son menos de 1 (recuerdan que $alpha ge 1$ ). Así, esta última declaración es verdadera y repitiendo nuestros pasos en orden inverso encontramos que $frac{d}{dx} ln{(1+x^alpha)} leq frac{d}{dx} (alpha x)$ para todos $x$ . Esto completa la prueba.

Una prueba alternativa es observar que ${displaystyle (1+x^{alpha })leq (1+x)^{alpha }}$ en las condiciones dadas. Esto puede probarse, por ejemplo, por las desigualdades de la norma. Tomando logaritmos y utilizando ${displaystyle ln(1+x)leq x}$ completa la prueba.

Derivado

La derivada del logaritmo natural como una función de valor real sobre los reales positivos viene dada por

frac{d}{dx} ln x = frac{1}{x}.

Cómo establecer esta derivada del logaritmo natural depende de cómo se defina de primera mano. Si el logaritmo natural se define como la integral

{displaystyle ln x=int _{1}^{x}{frac {1}{t}},dt,}

entonces la derivada se sigue inmediatamente de la primera parte del teorema fundamental del cálculo.

Por otro lado, si el logaritmo natural se define como el inverso de la función exponencial (natural), entonces el derivado (para x ■ 0) se puede encontrar utilizando las propiedades del logaritmo y una definición de la función exponencial. De la definición del número ${displaystyle e=lim _{uto 0}(1+u)^{1/u},}$ la función exponencial se puede definir como ${displaystyle e^{x}=lim _{uto 0}(1+u)^{x/u}=lim _{hto 0}(1+hx)^{1/h}}$ , donde ${displaystyle u=hx,h=u/x.}$ El derivado se puede encontrar a partir de los primeros principios.

{displaystyle {begin{aligned}{frac {d}{dx}}ln x&=lim _{hto 0}{frac {ln(x+h)-ln x}{h}}\&=lim _{hto 0}left[{frac {1}{h}}ln left({frac {x+h}{x}}right)right]\&=lim _{hto 0}left[ln left(left(1+{frac {h}{x}}right)^{frac {1}{h}}right)right]quad &&{text{all above for logarithmic properties}}\&=ln left[lim _{hto 0}left(1+{frac {h}{x}}right)^{frac {1}{h}}right]quad &&{text{for continuity of the logarithm}}\&=ln e^{1/x}quad &&{text{for the definition of }}e^{x}=lim _{hto 0}(1+hx)^{1/h}\&={frac {1}{x}}quad &&{text{for the definition of the ln as inverse function.}}end{aligned}}}

Además, tenemos:

{displaystyle {frac {d}{dx}}ln ax={frac {d}{dx}}(ln a+ln x)={frac {d}{dx}}ln a+{frac {d}{dx}}ln x={frac {1}{x}}.}

así que, a diferencia de su función inversa $e^{{ax}}$ , una constante en la función no altera el diferencial.

Serie

Los polinomios Taylor para ln(1 +x) sólo proporcionan aproximaciones precisas en el rango −1x≤ 1. Más allá de algunos xLos polinomios Taylor de mayor grado son cada vez más peor aproximaciones.

Ya que el logaritmo natural es indefinido en 0, $ln(x)$ en sí mismo no tiene una serie Maclaurin, a diferencia de muchas otras funciones elementales. En cambio, uno busca expansións de Taylor alrededor de otros puntos. Por ejemplo, si ${displaystyle vert x-1vert leq 1{text{ and }}xneq 0,}$ entonces

{displaystyle {begin{aligned}ln x&=int _{1}^{x}{frac {1}{t}},dt=int _{0}^{x-1}{frac {1}{1+u}},du\&=int _{0}^{x-1}(1-u+u^{2}-u^{3}+cdots),du\&=(x-1)-{frac {(x-1)^{2}}{2}}+{frac {(x-1)^{3}}{3}}-{frac {(x-1)^{4}}{4}}+cdots \&=sum _{k=1}^{infty }{frac {(-1)^{k-1}(x-1)^{k}}{k}}.end{aligned}}}

Esta es la serie de Taylor para ln x alrededor de 1. Un cambio de variables produce la serie de Mercator:

{displaystyle ln(1+x)=sum _{k=1}^{infty }{frac {(-1)^{k-1}}{k}}x^{k}=x-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-cdots}

válido para |x| ≤ 1 y x ≠ −1.

Leonhard Euler, ignorando ${displaystyle xneq -1}$ , sin embargo aplicó esta serie x= −1, para mostrar que la serie armónica equivale al logaritmo (natural) de 1/(1 −1), es decir, el logaritmo de la infinidad. Hoy en día, más formalmente, se puede probar que la serie armónica truncada en N está cerca del logaritmo de N, cuando N es grande, con la diferencia convergente a la constante Euler–Mascheroni.

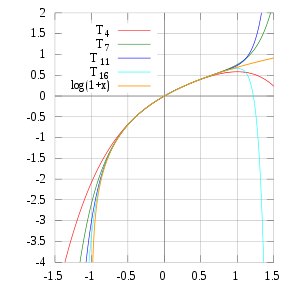
A la derecha hay una imagen de ln(1 + x) y algunos de sus polinomios de Taylor alrededor de 0. Estas aproximaciones convergen a la función solo en la región −1 < x ≤ 1; fuera de esta región, los polinomios de Taylor de mayor grado evolucionan hacia aproximaciones peores para la función.

Un caso especial útil para números enteros positivos n, tomar ${displaystyle x={tfrac {1}{n}}}$ , es:

{displaystyle ln left({frac {n+1}{n}}right)=sum _{k=1}^{infty }{frac {(-1)^{k-1}}{kn^{k}}}={frac {1}{n}}-{frac {1}{2n^{2}}}+{frac {1}{3n^{3}}}-{frac {1}{4n^{4}}}+cdots }

Si ${displaystyle operatorname {Re} (x)geq 1/2,}$ entonces

{displaystyle {begin{aligned}ln(x)&=-ln left({frac {1}{x}}right)=-sum _{k=1}^{infty }{frac {(-1)^{k-1}({frac {1}{x}}-1)^{k}}{k}}=sum _{k=1}^{infty }{frac {(x-1)^{k}}{kx^{k}}}\&={frac {x-1}{x}}+{frac {(x-1)^{2}}{2x^{2}}}+{frac {(x-1)^{3}}{3x^{3}}}+{frac {(x-1)^{4}}{4x^{4}}}+cdots end{aligned}}}

Ahora, tomando ${displaystyle x={tfrac {n+1}{n}}}$ para números enteros positivos n, tenemos:

{displaystyle ln left({frac {n+1}{n}}right)=sum _{k=1}^{infty }{frac {1}{k(n+1)^{k}}}={frac {1}{n+1}}+{frac {1}{2(n+1)^{2}}}+{frac {1}{3(n+1)^{3}}}+{frac {1}{4(n+1)^{4}}}+cdots }

Si ${displaystyle operatorname {Re} (x)geq 0{text{ and }}xneq 0,}$ entonces

{displaystyle ln(x)=ln left({frac {2x}{2}}right)=ln left({frac {1+{frac {x-1}{x+1}}}{1-{frac {x-1}{x+1}}}}right)=ln left(1+{frac {x-1}{x+1}}right)-ln left(1-{frac {x-1}{x+1}}right).}

Desde

{displaystyle {begin{aligned}ln(1+y)-ln(1-y)&=sum _{i=1}^{infty }{frac {1}{i}}left((-1)^{i-1}y^{i}-(-1)^{i-1}(-y)^{i}right)=sum _{i=1}^{infty }{frac {y^{i}}{i}}left((-1)^{i-1}+1right)\&=ysum _{i=1}^{infty }{frac {y^{i-1}}{i}}left((-1)^{i-1}+1right){overset {i-1to 2k}{=}};2ysum _{k=0}^{infty }{frac {y^{2k}}{2k+1}},end{aligned}}}

Llegamos a

{displaystyle {begin{aligned}ln(x)&={frac {2(x-1)}{x+1}}sum _{k=0}^{infty }{frac {1}{2k+1}}{left({frac {(x-1)^{2}}{(x+1)^{2}}}right)}^{k}\&={frac {2(x-1)}{x+1}}left({frac {1}{1}}+{frac {1}{3}}{frac {(x-1)^{2}}{(x+1)^{2}}}+{frac {1}{5}}{left({frac {(x-1)^{2}}{(x+1)^{2}}}right)}^{2}+cdots right).end{aligned}}}

Utilizando la sustitución ${displaystyle x={tfrac {n+1}{n}}}$ de nuevo para números enteros positivos n, tenemos:

{displaystyle {begin{aligned}ln left({frac {n+1}{n}}right)&={frac {2}{2n+1}}sum _{k=0}^{infty }{frac {1}{(2k+1)((2n+1)^{2})^{k}}}\&=2left({frac {1}{2n+1}}+{frac {1}{3(2n+1)^{3}}}+{frac {1}{5(2n+1)^{5}}}+cdots right).end{aligned}}}

Esta es, con mucho, la convergencia más rápida de la serie descrita aquí.

El logaritmo natural también se puede expresar como un producto infinito:

{displaystyle ln(x)=(x-1)prod _{k=1}^{infty }left({frac {2}{1+{sqrt[{2^{k}}]{x}}}}right)}

Dos ejemplos podrían ser:

{displaystyle ln(2)=left({frac {2}{1+{sqrt {2}}}}right)left({frac {2}{1+{sqrt[{4}]{2}}}}right)left({frac {2}{1+{sqrt[{8}]{2}}}}right)left({frac {2}{1+{sqrt[{16}]{2}}}}right)...}

{displaystyle pi =(2i+2)left({frac {2}{1+{sqrt {i}}}}right)left({frac {2}{1+{sqrt[{4}]{i}}}}right)left({frac {2}{1+{sqrt[{8}]{i}}}}right)left({frac {2}{1+{sqrt[{16}]{i}}}}right)...}

De esta identidad, podemos obtener fácilmente que:

{displaystyle {frac {1}{ln(x)}}={frac {x}{x-1}}-sum _{k=1}^{infty }{frac {2^{-k}x^{2^{-k}}}{1+x^{2^{-k}}}}}

Por ejemplo:

{displaystyle {frac {1}{ln(2)}}=2-{frac {sqrt {2}}{2+2{sqrt {2}}}}-{frac {sqrt[{4}]{2}}{4+4{sqrt[{4}]{2}}}}-{frac {sqrt[{8}]{2}}{8+8{sqrt[{8}]{2}}}}cdots }

El logaritmo natural en la integración

El logaritmo natural permite la integración simple de funciones de la forma g(x) = f '(x )/f(x): una antiderivada de g(x) viene dada por ln (|f(x)|). Este es el caso debido a la regla de la cadena y al siguiente hecho:

{displaystyle {frac {d}{dx}}ln left|xright|={frac {1}{x}}.}

En otras palabras, si $x$ es un número real con $xnot =0$ , entonces

{displaystyle int {frac {1}{x}},dx=ln |x|+C}

{displaystyle int {{frac {f'(x)}{f(x)}},dx}=ln |f(x)|+C.}

Aquí hay un ejemplo en el caso de g(x) = tan(x):

{displaystyle {begin{aligned}&int tan x,dx=int {frac {sin x}{cos x}},dx\[6pt]&int tan x,dx=int {frac {-{frac {d}{dx}}cos x}{cos x}},dx.end{aligned}}}

Dejando f(x) = cos(x):

{displaystyle int tan x,dx=-ln left|cos xright|+C}

{displaystyle int tan x,dx=ln left|sec xright|+C}

donde C es una constante arbitraria de integración.

El logaritmo natural se puede integrar usando integración por partes:

{displaystyle int ln x,dx=xln x-x+C.}

Sea:

{displaystyle u=ln xRightarrow du={frac {dx}{x}}}

{displaystyle dv=dxRightarrow v=x}

entonces:

{displaystyle {begin{aligned}int ln x,dx&=xln x-int {frac {x}{x}},dx\&=xln x-int 1,dx\&=xln x-x+Cend{aligned}}}

Cómputo eficiente

Para ln(x) donde x > 1, cuanto más cerca esté el valor de x de 1, más rápida será la tasa de convergencia de su serie de Taylor centrada en 1. Las identidades asociadas con el logaritmo se pueden aprovechar para explotar esto:

{displaystyle {begin{aligned}ln 123.456&=ln(1.23456cdot 10^{2})\&=ln 1.23456+ln(10^{2})\&=ln 1.23456+2ln 10\&approx ln 1.23456+2cdot 2.3025851.end{aligned}}}

Tales técnicas se usaban antes de las calculadoras, haciendo referencia a tablas numéricas y realizando manipulaciones como las anteriores.

Logaritmo natural de 10

El logaritmo natural de 10, que tiene la expansión decimal 2,30258509..., desempeña un papel, por ejemplo, en el cálculo de logaritmos naturales de números representados en notación científica, como una mantisa multiplicada por una potencia de 10:

{displaystyle ln(acdot 10^{n})=ln a+nln 10.}

Esto significa que uno puede calcular efectivamente los logaritmos de números con una magnitud muy grande o muy pequeña usando los logaritmos de un conjunto relativamente pequeño de decimales en el rango $[1, 10)$ .

Alta precisión

Para calcular el logaritmo natural con muchos dígitos de precisión, el enfoque de la serie de Taylor no es eficiente ya que la convergencia es lenta. Especialmente si $x$ está cerca de 1, una buena alternativa es usar el método de Halley o el método de Newton para invertir la función exponencial., porque la serie de la función exponencial converge más rápidamente. Para encontrar el valor de $y$ para dar $exp(y) - x = 0$ usando el método de Halley, o de manera equivalente para dar $exp(y /2) - x exp(- y /2) = 0$ usando el método de Newton, la iteración se simplifica a

{displaystyle y_{n+1}=y_{n}+2cdot {frac {x-exp(y_{n})}{x+exp(y_{n})}}}

que tiene convergencia cúbica a $ln(x)$ .

Otra alternativa para el cálculo de precisión extremadamente alta es la fórmula

ln x approx frac{pi}{2 M(1,4/s)} - m ln 2,

donde $M$ denota la media aritmético-geométrica de 1 y $4/ s$ , y

2^{p/2},}" xmlns="http://www.w3.org/1998/Math/MathML">s=x2m■2p/2,{displaystyle s=x2^{m} {p/2}2^{p/2},}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e97043486e689440687aae21cc96aae4c4aa8c0b" style="vertical-align: -0.671ex; width:15.967ex; height:3.176ex;"/>

con $m$ elegido para que $p$ bits de precisión se logra (Para la mayoría de los propósitos, el valor de 8 para m es suficiente). De hecho, si se usa este método, la inversión de Newton del logaritmo natural puede usarse a la inversa para calcular la función exponencial de manera eficiente. (Las constantes ln 2 y π se pueden precalcular con la precisión deseada usando cualquiera de varias series conocidas de convergencia rápida). O se puede usar la siguiente fórmula:

{displaystyle ln x={frac {pi }{Mleft(theta _{2}^{2}(1/x),theta _{3}^{2}(1/x)right)}},quad xin (1,infty)}

dónde

{displaystyle theta _{2}(x)=sum _{nin mathbb {Z} }x^{(n+1/2)^{2}},quad theta _{3}(x)=sum _{nin mathbb {Z} }x^{n^{2}}}

son las funciones theta de Jacobi.

Basado en una propuesta de William Kahan e implementada por primera vez en la calculadora Hewlett-Packard HP-41C en 1979 (referida bajo "LN1" en la pantalla, únicamente), algunas calculadoras, sistemas operativos (para ejemplo Berkeley UNIX 4.3BSD), los sistemas de álgebra computacional y los lenguajes de programación (por ejemplo C99) proporcionan una función especial de logaritmo natural más 1, denominada alternativamente LNP1 o log1p para dar resultados más precisos para logaritmos cercanos a cero pasando argumentos x, también cercanos a cero, a una función log1p(x), que devuelve el valor ln(1+x), en lugar de pasar un valor y cercano a 1 a una función que devuelve ln(y). La función log1p evita en la aritmética de coma flotante una casi cancelación del término absoluto 1 con el segundo término de la expansión de Taylor de ln. Esto mantiene el argumento, el resultado y los pasos intermedios cerca de cero, donde se pueden representar con mayor precisión como números de punto flotante.

Además de la base $e$ , el estándar IEEE 754-2008 define funciones logarítmicas similares cercanas a 1 para logaritmos binarios y decimales: $log 2 (1 + x)$ y $log 10 (1 + x)$ .

Funciones inversas similares denominadas "expm1", "expm" o "exp1m" también existen, todos con el significado de $expm1(x) = exp(x) - 1$ .

Una identidad en términos de la tangente hiperbólica inversa,

{displaystyle mathrm {log1p} (x)=log(1+x)=2~mathrm {artanh} left({frac {x}{2+x}}right),,}

proporciona un valor de alta precisión para valores pequeños de $x$ en sistemas que no implementan $log1p(x)$ .

Complejidad computacional

La complejidad computacional de calcular el logaritmo natural utilizando la media aritmético-geométrica (para los dos métodos anteriores) es O(M(n) ln n). Aquí n es el número de dígitos de precisión con el que se evaluará el logaritmo natural y M(n) es la complejidad computacional de multiplicar dos números de n-dígitos.

Fracciones continuas

Si bien no hay fracciones continuas simples disponibles, existen varias fracciones continuas generalizadas, que incluyen:

{displaystyle {begin{aligned}ln(1+x)&={frac {x^{1}}{1}}-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-{frac {x^{4}}{4}}+{frac {x^{5}}{5}}-cdots \[5pt]&={cfrac {x}{1-0x+{cfrac {1^{2}x}{2-1x+{cfrac {2^{2}x}{3-2x+{cfrac {3^{2}x}{4-3x+{cfrac {4^{2}x}{5-4x+ddots }}}}}}}}}}end{aligned}}}

{displaystyle {begin{aligned}ln left(1+{frac {x}{y}}right)&={cfrac {x}{y+{cfrac {1x}{2+{cfrac {1x}{3y+{cfrac {2x}{2+{cfrac {2x}{5y+{cfrac {3x}{2+ddots }}}}}}}}}}}}\[5pt]&={cfrac {2x}{2y+x-{cfrac {(1x)^{2}}{3(2y+x)-{cfrac {(2x)^{2}}{5(2y+x)-{cfrac {(3x)^{2}}{7(2y+x)-ddots }}}}}}}}end{aligned}}}

Estas fracciones continuas, en particular la última, convergen rápidamente para valores cercanos a 1. Sin embargo, los logaritmos naturales de números mucho más grandes se pueden calcular fácilmente sumando repetidamente los de números más pequeños, con una convergencia igualmente rápida.

Por ejemplo, dado que 2 = 1,25³ × 1,024, el logaritmo natural de 2 se puede calcular como:

{displaystyle {begin{aligned}ln 2&=3ln left(1+{frac {1}{4}}right)+ln left(1+{frac {3}{125}}right)\[8pt]&={cfrac {6}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {6}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}

Además, dado que 10 = 1,25¹⁰ × 1,024³, incluso el logaritmo natural de 10 se puede calcular de forma similar a:

{displaystyle {begin{aligned}ln 10&=10ln left(1+{frac {1}{4}}right)+3ln left(1+{frac {3}{125}}right)\[10pt]&={cfrac {20}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {18}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}

El recíproco del logaritmo natural también se puede escribir de esta forma:

{displaystyle {frac {1}{ln(x)}}={frac {2x}{x^{2}-1}}{sqrt {{frac {1}{2}}+{frac {x^{2}+1}{4x}}}}{sqrt {{frac {1}{2}}+{frac {1}{2}}{sqrt {{frac {1}{2}}+{frac {x^{2}+1}{4x}}}}}}ldots }

Por ejemplo:

{displaystyle {frac {1}{ln(2)}}={frac {4}{3}}{sqrt {{frac {1}{2}}+{frac {5}{8}}}}{sqrt {{frac {1}{2}}+{frac {1}{2}}{sqrt {{frac {1}{2}}+{frac {5}{8}}}}}}ldots }

Logaritmos complejos

La función exponencial se puede extender a una función que da un número complejo como $e z$ para cualquier número complejo arbitrario $z$ ; simplemente use la serie infinita con $x$ =z complejo. Esta función exponencial se puede invertir para formar un logaritmo complejo que exhibe la mayoría de las propiedades del logaritmo ordinario. Hay dos dificultades involucradas: ninguna $x$ tiene $e x = 0$ ; y resulta que $e 2 iπ = 1 = e 0$ . Dado que la propiedad multiplicativa todavía funciona para la función exponencial compleja, $e z = e z +2 kiπ$ , para todos los complejos $z$ y enteros $k$ .

Por lo tanto, el logaritmo no se puede definir para todo el plano complejo, e incluso entonces tiene varios valores: cualquier logaritmo complejo se puede cambiar a un "equivalente" logaritmo sumando cualquier entero múltiplo de $2 iπ$ a voluntad. El logaritmo complejo solo puede tener un valor único en el plano de corte. Por ejemplo, $ln i = iπ / 2$ o $5 iπ / 2$ o $- 3 iπ / 2, etc.; y aunque i 4 = 1, 4 ln i se puede definir como 2 iπ, o 10 iπ o -6 iπ, y así sucesivamente.$

Parcelas de la función de logaritmo natural en el plano complejo (la rama principal)
$z = Re(ln(x + Yi)$
$z = Silencio (Im(ln) x + Yi)) Silencio$
$z = Silencio (Ln(x + Yi) Silencio$
Superposición de los tres gráficos anteriores

Contenido relacionado

Más resultados...