Ley de Wien (desplazamiento)

Ajustar Compartir Imprimir Citar

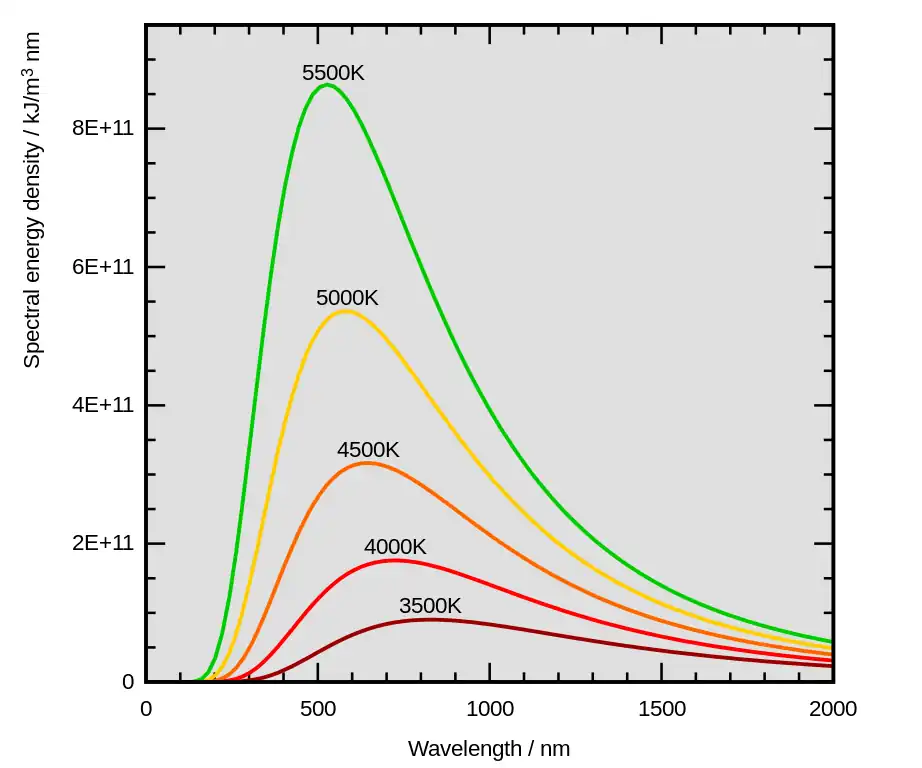
Radiación de cuerpo negro en función de la longitud de onda para diferentes temperaturas. La Ley de Wien describe por qué se mueve el pico de radiación.

La Ley de Wien es un principio fundamental de la física que describe cómo varía la radiación de un cuerpo negro con la temperatura, estableciendo que: el punto máximo de emisión de radiación de un cuerpo negro se desplaza hacia longitudes de onda cada vez más cortas (de mayor frecuencia) a medida que aumenta la temperatura, o en otras palabras: la longitud de onda en la que un cuerpo negro alcanza su pico de radiación es inversamente proporcional a la temperatura. Esta Ley fue formulada en 1893 por Wilhelm Wien, de allí su nombre.

La ley se expresa matemáticamente indicando que la longitud de onda máxima de la radiancia espectral (λ_max) está inversamente relacionada con la temperatura absoluta (T) del objeto. La fórmula es λ_max = b / T, donde b es la constante de desplazamiento de Wien, valorada en aproximadamente 2,897771955 × 10^-3 m·K o b ≈ 2898 μm⋅K.

Formulada antes que la Ley de Radiación de Planck (1900), la Ley de Wien fue un avance crucial para entender la radiación espectral. Ambas leyes abordan la intensidad de la radiación de un cuerpo negro en función de la longitud de onda a una temperatura dada.

Esta relación inversa entre longitud de onda de la radiación térmica y temperatura explica por qué objetos más calientes emiten radiación en longitudes de onda más cortas. Por ejemplo, a temperaturas altas, los objetos pueden emitir luz visible con tonos azulados, mientras que a temperaturas más bajas, la emisión se desplaza hacia el rojo o incluso más allá, hacia el espectro infrarrojo.

La Ley de Wien no solo aplica para determinar la longitud de onda de máxima emisión, sino también ofrece claridad sobre la relación entre frecuencia máxima de emisión y la temperatura, siendo estas dos directamente proporcionales. Aunque se descubrió en el contexto de la radiación de cuerpo negro, sus implicaciones se extienden a diversas áreas de la física y la astronomía, proveyendo una herramienta esencial para el análisis espectral y el estudio de propiedades térmicas de los cuerpos.

Wien formuló también otra ecuación, la Aproximación de Wien (1896), combinando este conocimiento con los modelos para átomos de distribución de energía de Maxwell–Boltzmann. Esta ecuación resultó ser excepcionalmente útil para simplificar la Ley de Planck cuando se trabaja con el límite de longitudes de onda cortas (o altas frecuencias), de donde tomó su nombre como una "aproximación a la Ley de Planck". En campos especializados se le conoce también como Ley de Wien (sobre distribución).

La importancia de la Ley de Wien en el estudio de la termodinámica y la radiación electromagnética, es que permitió comprender cómo la temperatura afecta la radiación emitida por los cuerpos, un conocimiento útil tanto para la física teórica como para aplicaciones industriales o la observación astronómica.

HSD

Ejemplos

La ley de desplazamiento de Wien es relevante para algunas experiencias cotidianas:

Un pedazo de metal calentado por una antorcha de soplado se convierte primero en "rojo caliente" ya que las longitudes de onda visibles más largas parecen rojas, entonces se vuelve más naranja-rojo a medida que aumenta la temperatura, y a temperaturas muy altas se describiría como "blanco caliente" como longitudes de onda más cortas y más cortas llegan a predominar el espectro de emisiones de cuerpo negro. Antes de que incluso hubiera alcanzado la temperatura caliente roja, la emisión térmica era principalmente a longitudes de onda infrarrojas más largas, que no son visibles; sin embargo, que la radiación se podía sentir ya que calienta la piel cercana.
Se observa fácilmente cambios en el color de una bombilla incandescente (que produce luz a través de la radiación térmica) ya que la temperatura de su filamento es variada por un dimmer de luz. A medida que la luz se disminuye y la temperatura del filamento disminuye, la distribución del color cambia hacia longitudes de onda más largas y la luz aparece más roja, así como el martillo.
Un fuego de madera a 1500 K pone a la radiación pico alrededor de 2000 nanometros. El 98% de su radiación es de longitudes de onda más de 1000 nm, y sólo una pequeña proporción en longitudes de onda visibles (390–700 nanometros). En consecuencia, una fogata puede mantener un fuego cálido pero es una fuente pobre de luz visible.
La temperatura efectiva del Sol es de 5778 Kelvin. Usando la ley de Wien, se encuentra una emisión máxima por nanometro (de longitud de onda) a una longitud de onda de unos 500 nm, en la parte verde del espectro cerca de la sensibilidad máxima del ojo humano. Por otro lado, en términos de potencia por unidad de frecuencia óptica, la emisión máxima del Sol es de 343 THz o una longitud de onda de 883 nm en el infrarrojo cercano. En términos de potencia por porcentaje de ancho de banda, el pico es alrededor de 635 nm, una longitud de onda roja. Independientemente de cómo se quiere trazar el espectro, alrededor de la mitad de la radiación del sol está en longitudes de onda más cortas que 710 nm, sobre el límite de la visión humana. De eso, alrededor del 12% está en longitudes de onda más cortas que 400 nm, longitudes de onda ultravioleta, que es invisible a un ojo humano no identificado. Se puede apreciar que una cantidad bastante grande de la radiación del Sol cae en el espectro visible bastante pequeño.

El color de una estrella está determinado por su temperatura, según la ley de Wien. En la constelación de Orión, se puede comparar Betelgeuse (T≈ 3300 K, superior izquierda), Rigel (T= 12100 K, inferior derecha), Bellatrix (T= 22000 K, superior derecha), y Mintaka (T= 31800 K, la más derecha de las 3 "estrellas inteligentes" en el medio).

La preponderancia de la emisión en el rango visible, sin embargo, no es el caso en la mayoría de las estrellas. El supergiant Rigel caliente emite el 60% de su luz en el ultravioleta, mientras que el supergiant Betelgeuse fresco emite el 85% de su luz en longitudes de onda infrarroja. Con ambas estrellas prominentes en la constelación de Orión, se puede apreciar fácilmente la diferencia de color entre el azul-blanco Rigel (T= 12100 K) y el Betelgeuse rojo (TEntendido 3300 K). Mientras que pocas estrellas son tan calientes como Rigel, las estrellas más frías que el sol o incluso tan cool como Betelgeuse son muy comunes.
Los mamíferos con una temperatura de la piel de alrededor de 300 K emiten radiación pico alrededor de 10 μm en el infrarrojo lejano. Por lo tanto, esta es la gama de longitudes de onda infrarrojas que se enfrentan a víboras y cámaras de IR pasivas deben sentir.
Al comparar el color aparente de las fuentes de iluminación (incluyendo luces fluorescentes, iluminación LED, monitores de computadora y fotoflash), es habitual citar la temperatura de color. Aunque el espectro de tales luces no se describe con precisión por la curva de radiación del cuerpo negro, se cita una temperatura de color (la temperatura de color correlacionada) para la cual la radiación del cuerpo negro encajaría más estrechamente con el color subjetivo de esa fuente. Por ejemplo, la luz fluorescente azul-blanca a veces utilizada en una oficina puede tener una temperatura de color de 6500 K, mientras que el tinte rojizo de una luz incandescente desmontada puede tener una temperatura de color (y una temperatura de filamento real) de 2000 K. Tenga en cuenta que la descripción informal del color antiguo (bluish) como "cool" y el último (rojo) como "warm" es exactamente opuesto al cambio de temperatura real implicado en la radiación del cuerpo negro.

Diferencias entre la Ley de Wien y la Aproximación de Wien

La Ley de Desplazamiento de Wien y la Aproximación de Wien están estrechamente relacionadas pero se aplican en contextos distintos dentro de la física del cuerpo negro.

La Ley de Desplazamiento de Wien se centra en la relación entre la temperatura de un cuerpo negro y la longitud de onda en la que su radiación es máxima. Esta ley establece que la longitud de onda de pico (λmax) de la radiación emitida por un cuerpo negro es inversamente proporcional a su temperatura (T), lo que significa que a medida que aumenta la temperatura, la longitud de onda de máxima emisión se desplaza hacia longitudes de onda más cortas. Esta relación se expresa mediante la fórmula λpico=T/b, donde b es la constante de desplazamiento de Wien.

Por otro lado, la Aproximación de Wien es una simplificación de la ley de radiación de Planck en el límite de longitudes de onda cortas (o altas frecuencias). La ley de Planck describe la radiación de un cuerpo negro a diferentes longitudes de onda y temperaturas, pero resulta matemáticamente compleja. La aproximación de Wien proporciona una expresión simplificada para calcular la intensidad de la radiación en este límite, resultando útil para analizar el comportamiento de la radiación en longitudes de onda cortas sin recurrir a la ecuación completa de Planck.

Diferencias Clave

Enfoque: La Ley de Desplazamiento se enfoca en la longitud de onda donde la radiación es máxima en función de la temperatura, mientras que la Aproximación de Wien simplifica la descripción de la intensidad de la radiación a lo largo de todo el espectro en longitudes de onda cortas.
Aplicación: La Ley de Desplazamiento es útil para determinar el cambio en la longitud de onda de máxima emisión con la temperatura. La Aproximación de Wien se aplica para estimar la intensidad de la radiación en el límite de altas frecuencias, donde se considera que la ley de Planck puede ser demasiado compleja para cálculos prácticos.
Fundamento Teórico: La Ley de Desplazamiento de Wien se basa en observaciones empíricas y análisis teóricos de la radiación del cuerpo negro, mientras que la Aproximación de Wien es una simplificación matemática de la ley de Planck para facilitar el análisis en ciertos límites del espectro.

Ambas son herramientas valiosas en el estudio de la física del cuerpo negro, cada una con su propósito específico y contexto de aplicación dentro de la termodinámica y la física cuántica.

Descubrimiento

La ley lleva el nombre de Wilhelm Wien, quien la derivó en 1893 basándose en un argumento termodinámico. Wien consideró la expansión adiabática de una cavidad que contenía ondas de luz en equilibrio térmico. Usando el principio de Doppler, demostró que, bajo una expansión o contracción lenta, la energía de la luz que se refleja en las paredes cambia exactamente de la misma manera que la frecuencia. Un principio general de la termodinámica es que un estado de equilibrio térmico, cuando se expande muy lentamente, permanece en equilibrio térmico.

El mismo Wien dedujo teóricamente esta ley en 1893, siguiendo el razonamiento termodinámico de Boltzmann. Anteriormente había sido observado, al menos semicuantitativamente, por un astrónomo estadounidense, Langley. Este cambio ascendente en $ν pico$ con $T$ es familiar para todos: cuando un hierro se calienta en un fuego, la primera radiación visible (alrededor de 900 K) es de color rojo intenso, la luz visible de frecuencia más baja. Un mayor aumento en T hace que el color cambie a naranja, luego a amarillo y finalmente a azul a temperaturas muy altas (10 000 K o más) para las cuales el pico en la intensidad de la radiación se ha movido más allá del visible hacia el ultravioleta.

El principio adiabático permitió a Wien concluir que para cada modo, la energía invariante adiabática/frecuencia es sólo una función de la otra invariante adiabática, la frecuencia/temperatura. De este modo, deriva la "versión fuerte" de la ley de desplazamiento de Wien: la afirmación de que el radiante espectral del cuerpo negro es proporcional a

.. 3F().. /T){displaystyle nu ^{3}F(nu /T)}

${displaystyle nu ^{3}F(nu /T)}$ para alguna función $F$ de una sola variable. Una variante moderna de la derivación de Wien se puede encontrar en el libro de texto de Wannier y en un papel de E. Buckingham

La consecuencia es que la forma de la función de radiación del cuerpo negro (que aún no se entendía) cambiaría proporcionalmente en frecuencia (o inversamente proporcional en longitud de onda) con la temperatura. Cuando Max Planck formuló más tarde la función correcta de radiación de cuerpo negro, no incluyó explícitamente la constante $b$ de Wien. Más bien, la constante de Planck $h$ fue creada e introducida en su nueva fórmula. De la constante de Planck $h$ y la constante de Boltzmann $k$ , se puede obtener la constante $b$ de Wien.

Formulación dependiente de la frecuencia

Para flujo espectral considerado por frecuencia de unidad

d.. {displaystyle dnu }

$dnu$ (en hertz), la ley de desplazamiento de Wien describe una emisión máxima a la frecuencia óptica

.. pico{displaystyle nu _{text{peak}}

${displaystyle nu _{text{peak}}}$ dado por:

.. pico=α α hkT.. ()5.879× × 1010Hz/K)⋅ ⋅ T{displaystyle nu _{text{peak}}={alpha over h}kTapprox (5.879times 10^{10}mathrm {Hz/K})cdot T}

{displaystyle nu _{text{peak}}={alpha over h}kTapprox (5.879times 10^{10} mathrm {Hz/K})cdot T}

o equivalente

h.. pico=α α kT.. ()2.431\times \times 10- - 4eV/K)\cdot \cdot T{displaystyle hnu ¿Por qué?

{displaystyle hnu _{text{peak}}=alpha kTapprox (2.431times 10^{-4} mathrm {eV/K})cdot T}

donde α = 2.821439372122 078893...< /span> es una constante resultante de la ecuación de maximización, $k$ es la constante de Boltzmann, $h$ es la constante de Planck y $T$ es la temperatura absoluta. Con la emisión ahora considerada por unidad de frecuencia, este pico ahora corresponde a una longitud de onda aproximadamente un 76% más larga que el pico considerado por unidad de longitud de onda. Las matemáticas relevantes se detallan en la siguiente sección.

Derivación de la Ley de Planck

La ley de Planck para el espectro de radiación de cuerpo negro predice la ley de desplazamiento de Wien y se puede utilizar para evaluar numéricamente la temperatura relativa constante y el valor del parámetro máximo para cualquier parametrización en particular. Comúnmente se utiliza una parametrización de longitud de onda y, en ese caso, la radiación espectral del cuerpo negro (potencia por área de emisión por ángulo sólido) es:

uλ λ ()λ λ ,T)=2hc2λ λ 51ehc/λ λ kT− − 1.{displaystyle u_{lambda }(lambdaT)={2hc^{2} over lambda ^{5}{1over e^{hc/lambda KT}-1}

u_{lambda }(lambdaT)={2hc^{2} over lambda ^{5}}{1 over e^{hc/lambda kT}-1}.

Derivar u(λ,T) con respecto a λ y establecer la derivada igual a cero da:

∂ ∂ u∂ ∂ λ λ =2hc2()hckTλ λ 7ehc/λ λ kT()ehc/λ λ kT− − 1)2− − 1λ λ 65ehc/λ λ kT− − 1)=0,{displaystyle {partial u over partial lambda }=2hc^{2}left({hc over kTlambda ^{7}{e^{hc/lambda kT} over left(e^{hc/lambda kT}-1right)^{2}}-{1 over lambda ^{6}{5 over e^{hc/lambda ¿Qué?

{displaystyle {partial u over partial lambda }=2hc^{2}left({hc over kTlambda ^{7}}{e^{hc/lambda kT} over left(e^{hc/lambda kT}-1right)^{2}}-{1 over lambda ^{6}}{5 over e^{hc/lambda kT}-1}right)=0,}

que se puede simplificar para dar:

hcλ λ kTehc/λ λ kTehc/λ λ kT− − 1− − 5=0.{displaystyle {hc over lambda kT}{e^{hc/lambda kT} over e^{hc/lambda KT}-1}-5=0.}

{hc over lambda kT}{e^{hc/lambda kT} over e^{hc/lambda kT}-1}-5=0.

Al definir:

x↑ ↑ hcλ λ kT,{displaystyle xequiv {hc over lambda kT},}

xequiv {hc over lambda kT},

la ecuación se convierte en una sola variable x:

xexex− − 1− − 5=0.{displaystyle {xe^{x} over e^{x}-1}-5=0}

{xe^{x} over e^{x}-1}-5=0.

que es equivalente a:

x=5()1− − e− − x).{displaystyle x=5(1-e^{-x}),}

{displaystyle x=5(1-e^{-x}),.}

Esta ecuación se resuelve mediante

x=5+W0()− − 5e− − 5){displaystyle x=5+W_{0}(-5e^{-5})}

{displaystyle x=5+W_{0}(-5e^{-5})}

Donde

W0{displaystyle W_{0}

$W_{0}$ es la rama principal de la función Lambert W, y da x = 4.965114231744276303.... Resolver la longitud de onda λ en milímetros, y utilizando kelvins para los rendimientos de temperatura:

λ_pico = hc / xkT =2.897771955185172661mm⋅K) T.

Parametrización por frecuencia

Otra parametrización común es por frecuencia. La derivación que produce el valor del parámetro pico es similar, pero comienza con la forma de la ley de Planck en función de la frecuencia ν:

u.. ().. ,T)=2h.. 3c21eh.. /kT− − 1.{displaystyle u_{nu }(nuT)={2hnu ^{3}over c^{2}{1over e^{hnu /kT}}}}

{displaystyle u_{nu }(nuT)={2hnu ^{3} over c^{2}}{1 over e^{hnu /kT}-1}.}

El proceso anterior que usa esta ecuación produce:

− − h.. kTeh.. /kTeh.. /kT− − 1+3=0.{displaystyle -{hnu over kT}{e^{hnu /kT} over e^{hnu - ¿Qué?

{displaystyle -{hnu over kT}{e^{hnu /kT} over e^{hnu /kT}-1}+3=0.}

El resultado neto es:

x=3()1− − e− − x).{displaystyle x=3(1-e^{-x}),}

{displaystyle x=3(1-e^{-x}),.}

Esto se resuelve de manera similar con la función Lambert W:

x=3+W0()− − 3e− − 3){displaystyle x=3+W_{0}(-3e^{-3})}

{displaystyle x=3+W_{0}(-3e^{-3})}

dando x = 2,821439372122 078893...< /lapso>.

Resolver para ν produce:

._pico = xkT / h =0,05878925757646824946... THz⋅K⁻¹) ⋅ T.

Diferentes máximos según la parametrización

Observe que para una temperatura dada, la parametrización por frecuencia implica una longitud de onda máxima diferente a la parametrización por longitud de onda.

Por ejemplo, usando T = 6000 K y la parametrización por longitud de onda, la longitud de onda para la radiación espectral máxima es λ = 482,962 nm con la frecuencia correspondiente ν = 620,737 THz. Para la misma temperatura, pero parametrizando por frecuencia, la frecuencia para la radiación espectral máxima es ν = 352.735 THz con la longitud de onda correspondiente λ = 849,907 nm.

Estas funciones son funciones de densidad de radiancia, que son funciones de densidad de probabilidad escaladas para dar unidades de radiancia. La función de densidad tiene diferentes formas para diferentes parametrizaciones, dependiendo del estiramiento o compresión relativa de la abscisa, que mide el cambio en la densidad de probabilidad en relación con un cambio lineal en un parámetro dado. Dado que la longitud de onda y la frecuencia tienen una relación recíproca, representan cambios significativamente no lineales en la densidad de probabilidad entre sí.

La radiancia total es la integral de la distribución sobre todos los valores positivos, y eso es invariable para una temperatura dada bajo cualquier parametrización. Además, para una temperatura dada, la radiación que consiste en todos los fotones entre dos longitudes de onda debe ser la misma, independientemente de la distribución que utilice. Es decir, integrando la distribución de longitud de onda de λ₁ a λ₂ dará como resultado el mismo valor que integrando la distribución de frecuencias entre las dos frecuencias que corresponden a λ₁ y λ₂, concretamente de c/< i>λ₂ a c/λ₁. Sin embargo, la forma de la distribución depende de la parametrización y, para una parametrización diferente, la distribución normalmente tendrá una densidad máxima diferente, como demuestran estos cálculos.

Usando la ecuación implícita

x=4()1− − e− − x){displaystyle x=4(1-e^{-x})}

${displaystyle x=4(1-e^{-x})}$ produce el pico en la función de densidad de radiancia espectral expresada en el radiance del parámetro por ancho de banda proporcional. (Es decir, la densidad de radiación por frecuencia ancho de banda proporcional a la frecuencia misma, que se puede calcular considerando intervalos infinitesimal de $In .$ (o equivalente) $In λ$ ) en lugar de la frecuencia misma.) Esta es tal vez una forma más intuitiva de presentar "la longitud de onda de emisión pico". Eso produce x = 3.920690394872886343....

Sin embargo, el punto importante de la ley de Wien es que cualquier marcador de longitud de onda, incluida la longitud de onda mediana (o, alternativamente, la longitud de onda por debajo de la cual cualquier porcentaje especificado de la emisión ocurre) es proporcional al recíproco de la temperatura. Es decir, la forma de la distribución para una parametrización dada escala y se traduce de acuerdo con la temperatura, y puede calcularse una vez para una temperatura canónica, luego cambiarse y escalarse apropiadamente para obtener la distribución para otra temperatura. Esta es una consecuencia de la declaración fuerte de la ley de Wien.

Críticas

Marr y Wilkin (2012) sostienen que la enseñanza generalizada de la ley de desplazamiento de Wien en cursos introductorios es indeseable y sería mejor reemplazarla con material alternativo. Argumentan que enseñar derecho es problemático porque:

la curva de Planck es demasiado amplia para que el pico se destaque o se considere significativo;
la ubicación del pico depende de la parametrización, y citan varias fuentes que coinciden en que "la designación de cualquier pico de la función no es significativa y, por lo tanto, debería restarse importancia";
la ley no se utiliza para determinar temperaturas en la práctica real, sino que se confía en el uso directo de la función de Planck.

Sugieren que se presente la energía promedio de los fotones en lugar de la ley de desplazamiento de Wien, como un indicador físicamente más significativo de los cambios que ocurren con el cambio de temperatura. En este sentido, recomiendan analizar el número medio de fotones por segundo en relación con la ley de Stefan-Boltzmann. Recomiendan que el espectro de Planck se represente como una "densidad de energía espectral por distribución de ancho de banda fraccional", utilizando una escala logarítmica para la longitud de onda o la frecuencia.