Las leyes del movimiento de Newton

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Leyes en física sobre fuerza y movimiento

Las leyes de movimiento de Newton, combinadas con su ley de gravedad, permiten la predicción de cómo los planetas, lunas y otros objetos orbitan a través del Sistema Solar, y son una parte vital de la planificación del viaje espacial. Durante la misión del Apolo 8 de 1968, el astronauta Bill Anders tomó esta foto, Earthrise; en su camino de regreso a la Tierra, Anders comentó, "Creo que Isaac Newton está haciendo la mayor parte de la conducción ahora mismo."

Las leyes del movimiento de Newton son tres leyes básicas de la mecánica clásica que describen la relación entre el movimiento de un objeto y las fuerzas que actúan sobre él. Estas leyes se pueden parafrasear de la siguiente manera:

Un cuerpo permanece en reposo, o en movimiento a una velocidad constante en una línea recta, a menos que actúe por una fuerza.
Cuando un cuerpo es accionado por una fuerza, el tiempo de cambio de su impulso equivale a la fuerza.
Si dos cuerpos ejercen fuerzas entre sí, estas fuerzas tienen la misma magnitud pero direcciones opuestas.

Las tres leyes del movimiento fueron establecidas por primera vez por Isaac Newton en su Philosophiæ Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural), publicado originalmente en 1687. Newton los usó para investigar y explicar el movimiento de muchos objetos y sistemas físicos, lo que sentó las bases de la mecánica clásica. En el tiempo transcurrido desde Newton, el contenido conceptual de la física clásica se ha reformulado de formas alternativas, involucrando diferentes enfoques matemáticos que han producido ideas que estaban oscurecidas en la formulación newtoniana original. También se han descubierto limitaciones a las leyes de Newton; son necesarias nuevas teorías cuando los objetos se mueven a velocidades muy altas (relatividad especial), son muy masivos (relatividad general) o son muy pequeños (mecánica cuántica).

Requisitos

Las leyes de Newton a menudo se expresan en términos de masas de puntos o partículas, es decir, cuerpos cuyo volumen es insignificante. Esta es una aproximación razonable para cuerpos reales cuando se puede despreciar el movimiento de las partes internas y cuando la separación entre los cuerpos es mucho mayor que el tamaño de cada uno. Por ejemplo, la Tierra y el Sol pueden aproximarse como puntos cuando se considera la órbita del primero alrededor del segundo, pero la Tierra no es puntual cuando se consideran las actividades en su superficie.

La descripción matemática del movimiento, o cinemática, se basa en la idea de especificar posiciones utilizando coordenadas numéricas. El movimiento está representado por estos números que cambian con el tiempo: la trayectoria del cuerpo está representada por una función que asigna a cada valor de una variable de tiempo los valores de todas las coordenadas de posición. El caso más simple es unidimensional, es decir, cuando un cuerpo se limita a moverse sólo a lo largo de una línea recta. Su posición puede entonces ser dada por un solo número, indicando dónde es relativa a algún punto de referencia elegido. Por ejemplo, un cuerpo puede ser libre de deslizarse a lo largo de una pista que corre de izquierda a derecha, y por lo que su ubicación puede ser especificada por su distancia de un punto cero conveniente, o origen, con números negativos indicando posiciones a la izquierda y números positivos indicando posiciones a la derecha. Si la ubicación del cuerpo como función del tiempo es $s(t)$ , entonces su velocidad promedio a lo largo del intervalo de tiempo $t_{0}$ a $t_{1}$ es

{displaystyle {frac {Delta s}{Delta t}}={frac {s(t_{1})-s(t_{0})}{t_{1}-t_{0}}}.}

Delta

s

instantáneo

Delta

d

{displaystyle v={frac {ds}{dt}}.}

ds

dt

f(t)

L

t_{0}

f

L

t_{0}

{displaystyle lim _{tto t_{0}}f(t)=L.}

{displaystyle {frac {ds}{dt}}=lim _{Delta tto 0}{frac {s(t+Delta t)-s(t)}{Delta t}}.}

Aceleración

{displaystyle a={frac {dv}{dt}}=lim _{Delta tto 0}{frac {v(t+Delta t)-v(t)}{Delta t}}.}

segundo derivado

{displaystyle {frac {d^{2}s}{dt^{2}}}}

La posición, cuando se piensa como un desplazamiento desde un punto de origen, es un vector: una cantidad con magnitud y dirección. La velocidad y la aceleración también son cantidades vectoriales. Las herramientas matemáticas del álgebra vectorial proporcionan los medios para describir el movimiento en dos, tres o más dimensiones. Los vectores son a menudo denotados con una flecha, como en ${vec {s}}$ , o en negrita tipografía, como ${displaystyle {bf {s}}}$ . A menudo, los vectores se representan visualmente como flechas, con la dirección del vector siendo la dirección de la flecha, y la magnitud del vector indicado por la longitud de la flecha. Numéricamente, un vector puede ser representado como una lista; por ejemplo, un vector de velocidad del cuerpo puede ser ${displaystyle {vec {v}}=(mathrm {3~m/s}mathrm {4~m/s})}$ , indicando que se mueve a 3 metros por segundo a lo largo de un eje horizontal y 4 metros por segundo a lo largo del eje vertical. El mismo movimiento descrito en un sistema de coordenadas diferente será representado por diferentes números, y el álgebra vectorial se puede utilizar para traducir entre estas alternativas.

El concepto físico de fuerza convierte en cuantitativa la idea cotidiana de un empujón o un tirón. Las fuerzas en la mecánica newtoniana a menudo se deben a cuerdas y cuerdas, fricción, esfuerzo muscular, gravedad, etc. Al igual que el desplazamiento, la velocidad y la aceleración, la fuerza es una cantidad vectorial.

Leyes

Primero

Los satélites artificiales se mueven a lo largo de órbitas curvas, en lugar de en líneas rectas, debido a la gravedad de la Tierra.

Traducida del latín, la primera ley de Newton dice:

Cada cuerpo continúa en su estado de reposo, o de movimiento uniforme en una línea recta, a menos que se vea obligado a cambiar ese estado por fuerzas impresionadas.

La primera ley de Newton expresa el principio de inercia: el comportamiento natural de un cuerpo es moverse en línea recta a velocidad constante. En ausencia de influencias externas, el movimiento de un cuerpo preserva el statu quo.

La comprensión moderna de la primera ley de Newton es que ningún observador inercial tiene privilegio sobre ningún otro. El concepto de un observador inercial convierte en cuantitativa la idea cotidiana de no sentir los efectos del movimiento. Por ejemplo, una persona de pie en el suelo viendo pasar un tren es un observador inercial. Si el observador en tierra ve que el tren se mueve suavemente en línea recta a una velocidad constante, entonces un pasajero sentado en el tren también será un observador inercial: el pasajero del tren siente ningún movimiento. El principio expresado por la primera ley de Newton es que no hay manera de decir qué observador inercial es 'realmente' en movimiento y que es "realmente" quedarse quieto. El estado de reposo de un observador es el estado de movimiento uniforme en línea recta de otro observador, y ningún experimento puede considerar que ningún punto de vista es correcto o incorrecto. No existe un estándar absoluto de descanso.

Segundo

El cambio de movimiento de un objeto es proporcional a la fuerza impresionada; y se hace en la dirección de la línea recta en la que se impresiona la fuerza.

Por "movimiento", Newton se refería a la cantidad ahora llamada cantidad de movimiento, que depende de la cantidad de materia contenida en un cuerpo, la velocidad a la que se mueve ese cuerpo y la dirección en la que se mueve.. En notación moderna, el momento de un cuerpo es el producto de su masa por su velocidad:

{displaystyle {vec {p}}=m{vec {v}},.}

{displaystyle {vec {F}}={frac {d{vec {p}}}{dt}},.}

m

{displaystyle {vec {F}}=m{vec {a}},.}

{displaystyle {vec {F}}=m{frac {d^{2}}{dt^{2}}}{vec {s}},.}

Un diagrama de cuerpo libre para un bloque en un plano inclinado, ilustrando la fuerza normal perpendicular al plano (en inglés)N), la fuerza descendente de la gravedad (mg), y una fuerza f a lo largo de la dirección del plano que podría ser aplicado, por ejemplo, por una cuerda.

Las fuerzas que actúan sobre un cuerpo se suman como vectores, por lo que la fuerza total sobre un cuerpo depende tanto de las magnitudes como de las direcciones de las fuerzas individuales. Cuando la fuerza neta sobre un cuerpo es igual a cero, entonces, según la segunda ley de Newton, el cuerpo no acelera y se dice que está en equilibrio mecánico. Un estado de equilibrio mecánico es estable si, cuando la posición del cuerpo cambia ligeramente, el cuerpo permanece cerca de ese equilibrio. De lo contrario, el equilibrio es inestable.

Una representación visual común de las fuerzas que actúan en conjunto es el diagrama de cuerpo libre, que representa esquemáticamente un cuerpo de interés y las fuerzas que le aplican influencias externas. Por ejemplo, un diagrama de cuerpo libre de un bloque colocado sobre un plano inclinado puede ilustrar la combinación de fuerza gravitatoria, "normal" fuerza, fricción y tensión de la cuerda.

La segunda ley de Newton se presenta a veces como un definición de fuerza, es decir, una fuerza es la que existe cuando un observador inercial ve un cuerpo acelerando. Para que esto sea más que una tautología —la aceleración implica fuerza, fuerza implica aceleración— también se debe hacer otra declaración sobre la fuerza. Por ejemplo, una ecuación detallando la fuerza podría ser especificada, como la ley de Newton de la gravitación universal. Al insertar tal expresión para ${vec {F}}$ en la segunda ley de Newton, se puede escribir una ecuación con poder predictivo. La segunda ley de Newton también se ha considerado como establecer un programa de investigación para la física, estableciendo que los objetivos importantes del tema son identificar las fuerzas presentes en la naturaleza y catalogar los componentes de la materia.

Tercero

A cada acción, siempre se opone una reacción igual; o, las acciones mutuas de dos cuerpos sobre cada uno son siempre iguales, y dirigidas a partes contrarias.

Los cohetes funcionan produciendo una fuerte fuerza de reacción hacia abajo usando motores de cohetes. Esto empuja el cohete hacia arriba, sin tener en cuenta el suelo o la atmósfera.

Paráfrasis demasiado breves de la tercera ley, como "acción es igual a reacción" podría haber causado confusión entre generaciones de estudiantes: la "acción" y "reacción" aplicar a diferentes cuerpos. Por ejemplo, considere un libro en reposo sobre una mesa. La gravedad de la Tierra tira hacia abajo sobre el libro. La "reacción" a esa "acción" no es la fuerza de apoyo de la mesa que sostiene el libro, sino la atracción gravitacional del libro que actúa sobre la Tierra.

La tercera ley de Newton se refiere a un principio más fundamental, la conservación del impulso. Este último sigue siendo cierto incluso en los casos en que la declaración de Newton no, por ejemplo cuando los campos de fuerza y los cuerpos materiales llevan impulso, y cuando el impulso se define correctamente, en la mecánica cuántica también. En la mecánica newtoniana, si dos cuerpos tienen momentánea ${vec {p}}_{1}$ y ${vec {p}}_{2}$ respectivamente, entonces el impulso total del par es ${displaystyle {vec {p}}={vec {p}}_{1}+{vec {p}}_{2}}$ , y la tasa de cambio ${vec {p}}$ es

{displaystyle {frac {d{vec {p}}}{dt}}={frac {d{vec {p}}_{1}}{dt}}+{frac {d{vec {p}}_{2}}{dt}}.}

{vec {p}}

{vec {p}}

Candidatos para leyes adicionales

Varias fuentes han propuesto elevar otras ideas utilizadas en la mecánica clásica al estado de las leyes de Newton. Por ejemplo, en la mecánica newtoniana, la masa total de un cuerpo formado por la unión de dos cuerpos más pequeños es la suma de sus masas individuales. Frank Wilczek ha sugerido llamar la atención sobre esta suposición denominándola 'Ley Cero de Newton'. Otro candidato a una "ley cero" es el hecho de que en cualquier instante, un cuerpo reacciona a las fuerzas que se le aplican en ese instante. Asimismo, la idea de que las fuerzas se suman como vectores (o, en otras palabras, obedecen al principio de superposición), y la idea de que las fuerzas cambian la energía de un cuerpo, han sido descritas como una "cuarta ley".

Trabajo y energía

Los físicos desarrollaron el concepto de energía después de la época de Newton, pero se ha convertido en una parte inseparable de lo que se considera 'newtoniano'. física. La energía se puede clasificar en términos generales en cinética, debido al movimiento de un cuerpo, y potencial, debido a la posición de un cuerpo en relación con otros. La energía térmica, la energía transportada por el flujo de calor, es un tipo de energía cinética que no está asociada con el movimiento macroscópico de los objetos, sino con los movimientos de los átomos y las moléculas que los componen. De acuerdo con el teorema del trabajo y la energía, cuando una fuerza actúa sobre un cuerpo mientras ese cuerpo se mueve a lo largo de la línea de la fuerza, la fuerza trabaja sobre el cuerpo, y la cantidad de trabajo realizado es igual a el cambio en la energía cinética del cuerpo. En muchos casos de interés, el trabajo neto realizado por una fuerza cuando un cuerpo se mueve en un circuito cerrado, comenzando en un punto, moviéndose a lo largo de una trayectoria y regresando al punto inicial, es cero. Si este es el caso, entonces la fuerza se puede escribir en términos del gradiente de una función llamada potencial escalar:

{displaystyle {vec {F}}=-{vec {nabla }}U,.}

Ejemplos

Movimiento uniformemente acelerado

Una bola de rebote fotografiada en 25 marcos por segundo usando un flash estroboscópico. Entre los rebotes, la altura de la bola como función del tiempo está cerca de ser una parabola, desviando de un arco parabólico debido a la resistencia al aire, el giro y la deformación en forma no esférica sobre el impacto.

Si un cuerpo cae desde el reposo cerca de la superficie de la Tierra, entonces, en ausencia de resistencia del aire, acelerará a un ritmo constante. Esto se conoce como caída libre. La velocidad alcanzada durante la caída libre es proporcional al tiempo transcurrido, y la distancia recorrida es proporcional al cuadrado del tiempo transcurrido. Es importante destacar que la aceleración es la misma para todos los cuerpos, independientemente de su masa. Esto se deriva de combinar la segunda ley del movimiento de Newton con su ley de la gravitación universal. Este último establece que la magnitud de la fuerza gravitacional de la Tierra sobre el cuerpo es

{displaystyle F={frac {GMm}{r^{2}}},}

m

M

G

r

ma

m

G

M

r

r

g

{displaystyle g={frac {GM}{r^{2}}}approx mathrm {9.8~m/s^{2}}.}

Si el cuerpo no es liberado del descanso, sino lanzado hacia arriba y/o horizontalmente con velocidad no cero, entonces la caída libre se convierte en movimiento proyectil. Cuando se puede descuidar la resistencia al aire, los proyectiles siguen trayectorias en forma de parabola, porque la gravedad afecta al movimiento vertical del cuerpo y no a su horizontal. En el pico de la trayectoria del proyectil, su velocidad vertical es cero, pero su aceleración es $g$ hacia abajo, como es en todo momento. Establecer el vector equivocado igual a cero es una confusión común entre los estudiantes de física.

Movimiento circular uniforme

Dos objetos en movimiento circular uniforme, orbitando alrededor del barycenter (centro de masa de ambos objetos)

Cuando un cuerpo está en movimiento circular uniforme, la fuerza en él cambia la dirección de su movimiento pero no su velocidad. Para un cuerpo que se mueve en un círculo de radio $r$ a una velocidad constante $v$ , su aceleración tiene una magnitud

{displaystyle a={frac {v^{2}}{r}}}

{displaystyle mv^{2}/r}

{displaystyle GMm/r^{2}}

M

La bala de cañón de Newton es un experimento mental que interpola entre el movimiento de un proyectil y el movimiento circular uniforme. Una bala de cañón que se lanza débilmente desde el borde de un acantilado alto golpeará el suelo en la misma cantidad de tiempo que si se dejara caer desde el reposo, porque la fuerza de la gravedad solo afecta el impulso de la bala de cañón en la dirección hacia abajo. y su efecto no se ve disminuido por el movimiento horizontal. Si la bala de cañón se lanza con una velocidad horizontal inicial mayor, viajará más lejos antes de tocar el suelo, pero seguirá golpeando el suelo en la misma cantidad de tiempo. Sin embargo, si la bala de cañón se lanza con una velocidad inicial aún mayor, entonces la curvatura de la Tierra se vuelve significativa: el suelo mismo se curvará alejándose de la bala de cañón que cae. Una bala de cañón muy rápida se alejará de la trayectoria inercial en línea recta al mismo ritmo que la Tierra se curva debajo de ella; es decir, estará en órbita (imaginando que no se frena por la resistencia del aire ni por los obstáculos).

Movimiento armónico

oscilador armónico de cuerda de masa

movimiento armónico simple

Considerar un cuerpo de masa $m$ capaz de moverse a lo largo de la $x$ axis, y suponer que existe un punto de equilibrio en la posición $x=0$ . Es decir, $x=0$ , la fuerza neta sobre el cuerpo es el vector cero, y por la segunda ley de Newton, el cuerpo no acelerará. Si la fuerza sobre el cuerpo es proporcional al desplazamiento desde el punto de equilibrio, y dirigido al punto de equilibrio, entonces el cuerpo realizará un movimiento armónico simple. Escribir la fuerza como $F=-kx$ , la segunda ley de Newton se convierte

{displaystyle m{frac {d^{2}x}{dt^{2}}}=-kx,.}

{displaystyle x(t)=Acos omega t+Bsin omega t,}

omega

{sqrt {k/m}}

A

B

t=0

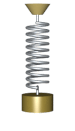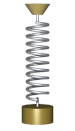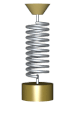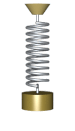
Una de las razones por las que el oscilador armónico es un ejemplo conceptualmente importante es que es una buena aproximación para muchos sistemas cerca de un equilibrio mecánico estable. Por ejemplo, un péndulo tiene un equilibrio estable en la posición vertical: si está inmóvil allí, permanecerá allí, y si se lo empuja ligeramente, se balanceará hacia adelante y hacia atrás. Despreciando la resistencia del aire y la fricción en el pivote, la fuerza sobre el péndulo es la gravedad, y la segunda ley de Newton se convierte en

{displaystyle {frac {d^{2}theta }{dt^{2}}}=-{frac {g}{L}}sin theta}

L

theta

theta

theta

theta

{displaystyle omega ={sqrt {g/L}}}

Un oscilador armónico puede ser amortiguado, a menudo por fricción o arrastre viscoso, en cuyo caso la energía sale del oscilador y la amplitud de las oscilaciones disminuye con el tiempo. Además, un oscilador armónico puede ser impulsado por una fuerza aplicada, lo que puede conducir al fenómeno de resonancia.

Objetos con masa variable

Rockets, como el transbordador espacial Atlantis, propelen la materia en una dirección para empujar la nave en la otra. Esto significa que la masa empujada, el cohete y su suministro de combustible a bordo restante, está cambiando constantemente.

La física newtoniana trata la materia como no ser creada ni destruida, aunque puede ser reorganizada. Puede ser el caso de que un objeto de interés gana o pierde masa porque la materia es agregada o eliminada de ella. En tal situación, las leyes de Newton se pueden aplicar a las piezas individuales de la materia, haciendo un seguimiento de cuáles piezas pertenecen al objeto de interés con el tiempo. Por ejemplo, si un cohete de masa $M(t)$ , moverse a velocidad ${vec {v}}(t)$ , los ejectos importan a una velocidad ${vec {u}}$ relativo al cohete, entonces

{displaystyle {vec {F}}=M{frac {d{vec {v}}}{dt}}-{vec {u}}{frac {dM}{dt}},}

{vec {F}}

Movimiento y rotación de cuerpos rígidos

Un cuerpo rígido es un objeto cuyo tamaño es demasiado grande para despreciarlo y que mantiene la misma forma a lo largo del tiempo. En la mecánica newtoniana, el movimiento de un cuerpo rígido a menudo se entiende separándolo en el movimiento del centro de masa del cuerpo y el movimiento alrededor del centro de masa.

Centro de masa

Fork-cork-toothpick object balanced on a pen on the toothpick part

El centro total de masa de los tenedores, el corcho y el palillo está encima de la punta de la pluma

Aspectos significativos del movimiento de un cuerpo extendido se pueden entender imaginando la masa de ese cuerpo concentrado a un solo punto, conocido como el centro de la masa. La ubicación del centro de masa de un cuerpo depende de cómo se distribuye el material de ese cuerpo. Para una colección de objetos puntiagudos con masas ${displaystyle m_{1},ldotsm_{N}}$ en puestos ${displaystyle {vec {r}}_{1},ldots{vec {r}}_{N}}$ , el centro de masa se encuentra en

{displaystyle {vec {R}}=sum _{i=1}^{N}{frac {m_{i}{vec {r}}_{i}}{M}},}

M

M

Análogos rotacionales de las leyes de Newton

Cuando las leyes de Newton se aplican a cuerpos extensos en rotación, conducen a nuevas cantidades que son análogas a las invocadas en las leyes originales. El análogo de la masa es el momento de inercia, la contraparte del momento es el momento angular y la contraparte de la fuerza es el par.

El impulso angular se calcula con respecto a un punto de referencia. Si el vector de desplazamiento de un punto de referencia a un cuerpo es ${vec {r}}$ y el cuerpo tiene impulso ${vec {p}}$ , entonces el impulso angular del cuerpo con respecto a ese punto es, utilizando el producto de la cruz vectorial,

{displaystyle {vec {L}}={vec {r}}times {vec {p}}.}

{displaystyle {frac {d{vec {L}}}{dt}}=left({frac {d{vec {r}}}{dt}}right)times {vec {p}}+{vec {r}}times {frac {d{vec {p}}}{dt}}={vec {v}}times m{vec {v}}+{vec {r}}times {vec {F}}.}

{vec {v}}

{displaystyle m{vec {v}}}

{displaystyle {vec {tau }}={vec {r}}times {vec {F}}.}

{displaystyle {vec {r}}=0}

{vec {F}}

{vec {r}}

El momento angular de un conjunto de masas puntuales y, por lo tanto, de un cuerpo extendido, se encuentra sumando las contribuciones de cada uno de los puntos. Esto proporciona un medio para caracterizar la rotación de un cuerpo alrededor de un eje, sumando los momentos angulares de sus piezas individuales. El resultado depende del eje elegido, la forma del cuerpo y la velocidad de rotación.

Sistema gravitatorio multicuerpo

Animación de tres puntos o cuerpos que se atraen entre sí

La ley de gravitación universal de Newton establece que cualquier cuerpo atrae a cualquier otro cuerpo a lo largo de la línea recta que los conecta. El tamaño de la fuerza de atracción es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellos. Encontrar la forma de las órbitas que producirá una ley de fuerza del cuadrado inverso se conoce como el problema de Kepler. El problema de Kepler se puede resolver de varias maneras, incluso demostrando que el vector de Laplace-Runge-Lenz es constante o aplicando una transformación de dualidad a un oscilador armónico bidimensional. Como sea que se resuelva, el resultado es que las órbitas serán secciones cónicas, es decir, elipses (incluyendo círculos), parábolas o hipérbolas. La excentricidad de la órbita, y por lo tanto el tipo de sección cónica, está determinada por la energía y el momento angular del cuerpo en órbita. Los planetas no tienen suficiente energía para escapar del Sol, por lo que sus órbitas son elipses, en una buena aproximación; debido a que los planetas se atraen entre sí, las órbitas reales no son exactamente secciones cónicas.

Si se agrega una tercera masa, el problema de Kepler se convierte en el problema de los tres cuerpos, que en general no tiene solución exacta en forma cerrada. Es decir, no hay forma de partir de las ecuaciones diferenciales implícitas en las leyes de Newton y, después de una secuencia finita de operaciones matemáticas estándar, obtener ecuaciones que expresen los tres cuerpos. movimientos a lo largo del tiempo. Se pueden aplicar métodos numéricos para obtener resultados útiles, aunque aproximados, para el problema de los tres cuerpos. Las posiciones y velocidades de los cuerpos se pueden almacenar en variables dentro de la memoria de una computadora; Las leyes de Newton se utilizan para calcular cómo cambiarán las velocidades en un breve intervalo de tiempo y, conociendo las velocidades, se pueden calcular los cambios de posición en ese intervalo de tiempo. Este proceso se repite para calcular, aproximadamente, los cuerpos' trayectorias. En términos generales, cuanto más corto sea el intervalo de tiempo, más precisa será la aproximación.

Caos e imprevisibilidad

Dinámica no lineal

Tres péndulos dobles, inicializados con casi exactamente las mismas condiciones iniciales, se sumergen con el tiempo.

Las leyes de movimiento de Newton permiten la posibilidad del caos. Es decir, cualitativamente hablando, los sistemas físicos que obedecen las leyes de Newton pueden exhibir una dependencia sensible de sus condiciones iniciales: un ligero cambio en la posición o la velocidad de una parte de un sistema puede conducir a que todo el sistema se comporte de una manera radicalmente diferente. Dentro de poco tiempo. Ejemplos dignos de mención incluyen el problema de los tres cuerpos, el péndulo doble, el billar dinámico y el problema de Fermi-Pasta-Ulam-Tsingou.

Las leyes de Newton se pueden aplicar a los fluidos considerando un líquido compuesto de piezas infinitesimal, cada fuerza que ejerce sobre las piezas vecinas. La ecuación del impulso de Euler es una expresión de la segunda ley de Newton adaptada a la dinámica del fluido. Un fluido es descrito por un campo de velocidad, es decir, una función ${displaystyle {vec {v}}({vec {x}},t)}$ que asigna un vector de velocidad a cada punto en el espacio y el tiempo. Un pequeño objeto que lleva el flujo de fluido puede cambiar la velocidad por dos razones: primero, porque el campo de velocidad en su posición está cambiando con el tiempo, y segundo, porque se mueve a una nueva ubicación donde el campo de velocidad tiene un valor diferente. En consecuencia, cuando la segunda ley de Newton se aplica a una porción infinitesimal de fluido, la aceleración ${vec {a}}$ tiene dos términos, una combinación conocida como un derivado total o material. La masa de una porción infinitesimal depende de la densidad del fluido, y hay una fuerza neta sobre ella si la presión del fluido varía de un lado a otro. En consecuencia, ${displaystyle {vec {a}}={vec {F}}/m}$ se convierte en

{displaystyle {frac {partial v}{partial t}}+({vec {nabla }}cdot {vec {v}}){vec {v}}=-{frac {1}{rho }}{vec {nabla }}P+{vec {f}},}

rho

P

{vec {f}}

{displaystyle {frac {partial v}{partial t}}+({vec {nabla }}cdot {vec {v}}){vec {v}}=-{frac {1}{rho }}{vec {nabla }}P+nu nabla ^{2}{vec {v}}+{vec {f}},}

nu

Singularidades

Es matemáticamente posible que un conjunto de masas puntuales, que se mueven de acuerdo con las leyes de Newton, lancen algunas de ellas con tanta fuerza que vuelen hacia el infinito en un tiempo finito. Este comportamiento no físico, conocido como "singularidad sin colisión", depende de que las masas sean puntuales y capaces de acercarse entre sí arbitrariamente, así como de la falta de un límite de velocidad relativista en la física newtoniana.

Todavía no se sabe si las ecuaciones de Euler y Navier-Stokes exhiben o no el comportamiento análogo de las soluciones inicialmente uniformes "explotando" tiempo infinito. La cuestión de la existencia y fluidez de las soluciones de Navier-Stokes es uno de los Problemas del Premio del Milenio.

Relación con otras formulaciones de la física clásica

La mecánica clásica se puede formular matemáticamente de múltiples formas diferentes, además de la "newtoniana" descripción (que, por supuesto, incorpora contribuciones de otros tanto antes como después de Newton). El contenido físico de estas diferentes formulaciones es el mismo que el newtoniano, pero brindan diferentes conocimientos y facilitan diferentes tipos de cálculos. Por ejemplo, la mecánica lagrangiana ayuda a hacer evidente la conexión entre las simetrías y las leyes de conservación, y es útil cuando se calcula el movimiento de cuerpos restringidos, como una masa restringida para moverse a lo largo de una pista curva o sobre la superficie de una esfera. La mecánica hamiltoniana es conveniente para la física estadística, conduce a una mayor comprensión de la simetría y puede desarrollarse en técnicas sofisticadas para la teoría de perturbaciones. Debido a la amplitud de estos temas, la discusión aquí se limitará a tratamientos concisos de cómo reformulan las leyes del movimiento de Newton.

Lagrangiano

La mecánica lagrangia difiere de la formulación Newtoniana considerando trayectorias enteras inmediatamente en lugar de predecir el movimiento de un cuerpo en un solo instante. Es tradicional en la mecánica lagrangiana para denotar posición con $q$ y velocidad con ${dot {q}}$ . El ejemplo más simple es una partícula de puntos masivos, la lagrangiana para la cual se puede escribir como la diferencia entre sus energías cinéticas y potenciales:

{displaystyle L(q,{dot {q}})=T-V,}

{displaystyle T={frac {1}{2}}m{dot {q}}^{2}}

V(q)

q_{i}

q_f

{displaystyle {frac {d}{dt}}left({frac {partial L}{partial {dot {q}}}}right)={frac {partial L}{partial q}}.}

{displaystyle {frac {d}{dt}}(m{dot {q}})=-{frac {dV}{dq}},}

Landau y Lifshitz argumentan que la formulación lagrangiana hace que el contenido conceptual de la mecánica clásica sea más claro que comenzar con las leyes de Newton. La mecánica lagrangiana proporciona un marco conveniente para probar el teorema de Noether, que relaciona las simetrías y las leyes de conservación. La conservación de la cantidad de movimiento se puede derivar aplicando el teorema de Noether a un Lagrangiano para un sistema de partículas múltiples, por lo que la tercera ley de Newton es un teorema en lugar de una suposición.

Hamiltoniano

Emmy Noether (1882-1935), que demostró un teorema celebrado que relaciona las simetrías y las leyes de conservación, un desarrollo clave en la física moderna que se indica convenientemente en el lenguaje de la mecánica lagrangiana o Hamiltoniana.

En la mecánica Hamiltoniana, la dinámica de un sistema está representada por una función llamada el Hamiltonian, que en muchos casos de interés es igual a la energía total del sistema. El Hamiltoniano es una función de las posiciones y el momenta de todos los cuerpos que componen el sistema, y también puede depender explícitamente del tiempo. Los derivados del tiempo de las variables de posición e impulso se dan por derivados parciales del Hamiltonian, a través de las ecuaciones de Hamilton. El ejemplo más simple es una masa de punto $m$ limitado a moverse en una línea recta, bajo el efecto de un potencial. Escritura $q$ para la coordinación y $p$ para el impulso del cuerpo, el Hamiltonian es

{displaystyle {mathcal {H}}(p,q)={frac {p^{2}}{2m}}+V(q).}

{displaystyle {frac {dq}{dt}}={frac {partial {mathcal {H}}}{partial p}}}

{displaystyle {frac {dp}{dt}}=-{frac {partial {mathcal {H}}}{partial q}}.}

{displaystyle {frac {dq}{dt}}={frac {p}{m}},}

{displaystyle {frac {dp}{dt}}=-{frac {dV}{dq}},}

Al igual que en la formulación lagrangiana, en la mecánica hamiltoniana la conservación de la cantidad de movimiento se puede derivar mediante el teorema de Noether, lo que convierte a la tercera ley de Newton en una idea que se deduce en lugar de suponerla.

Entre las propuestas para reformar el plan de estudios estándar de física introductoria se encuentra una que enseña el concepto de energía antes que el de fuerza, esencialmente "mecánica hamiltoniana introductoria".

Hamilton–Jacobi

La ecuación Hamilton-Jacobi ofrece otra formulación de la mecánica clásica, una que la hace matemáticamente análoga a la óptica de onda. Esta formulación también utiliza funciones Hamiltonianas, pero de manera diferente a la formulación descrita anteriormente. Los caminos tomados por cuerpos o colecciones de cuerpos se deducen de una función ${displaystyle S({vec {q}}_{1},{vec {q}}_{2},ldotst)}$ de posiciones ${displaystyle {vec {q}}_{i}}$ y tiempo $t$ . El Hamiltonian se incorpora en la ecuación Hamilton-Jacobi, una ecuación diferencial para $S$ . Los cuerpos se mueven con el tiempo de tal manera que sus trayectorias son perpendiculares a las superficies de constante $S$ , analógicamente a cómo un rayo de luz se propaga en la dirección perpendicular a su frente de onda. Esto es más sencillo de expresar para el caso de una sola masa de punto, en la que $S$ es una función ${displaystyle S({vec {q}},t)}$ , y la masa de punto se mueve en la dirección a lo largo de $S$ cambia más abruptamente. En otras palabras, el impulso de la masa de punto es el gradiente de $S$ :

{displaystyle {vec {v}}={frac {1}{m}}{vec {nabla }}S.}

{displaystyle -{frac {partial S}{partial t}}=Hleft({vec {q}},{vec {nabla }}S,tright).}

{displaystyle V({vec {q}})}

{displaystyle -{frac {partial S}{partial t}}={frac {1}{2m}}left({vec {nabla }}Sright)^{2}+V({vec {q}}).}

{displaystyle -{vec {nabla }}{frac {partial S}{partial t}}={frac {1}{2m}}{vec {nabla }}left({vec {nabla }}Sright)^{2}+{vec {nabla }}V.}

{displaystyle -{frac {partial }{partial t}}{vec {nabla }}S={frac {1}{m}}left({vec {nabla }}Scdot {vec {nabla }}right){vec {nabla }}S+{vec {nabla }}V.}

S

{displaystyle left[{frac {partial }{partial t}}+{frac {1}{m}}left({vec {nabla }}Scdot {vec {nabla }}right)right]{vec {nabla }}S=-{vec {nabla }}V.}

{displaystyle left[{frac {partial }{partial t}}+{frac {1}{m}}left({vec {nabla }}Scdot {vec {nabla }}right)right]=left[{frac {partial }{partial t}}+{vec {v}}cdot {vec {nabla }}right]={frac {d}{dt}}.}

Relación con otras teorías físicas

Termodinámica y física estadística

Una simulación de una partícula más grande, pero todavía microscópica (en amarillo) rodeada de un gas de partículas más pequeñas, que ilustra el movimiento marroniano.

En física estadística, la teoría cinética de los gases aplica las leyes de movimiento de Newton a grandes cantidades (normalmente del orden del número de Avogadro) de partículas. La teoría cinética puede explicar, por ejemplo, la presión que ejerce un gas sobre el recipiente que lo contiene como la suma de muchos impactos de átomos, cada uno de los cuales imparte una pequeña cantidad de impulso.

La ecuación de Langevin es un caso especial de la segunda ley de Newton, adaptada para el caso de describir un objeto pequeño bombardeado estocásticamente por otros aún más pequeños. Se puede escribir

{displaystyle m{vec {a}}=-gamma {vec {v}}+{vec {xi }},}

gamma

{vec {xi }}

Electromagnetismo

Las tres leyes de Newton se pueden aplicar a fenómenos relacionados con la electricidad y el magnetismo, aunque existen sutilezas y advertencias.

La ley de Coulomb para la fuerza eléctrica entre dos cuerpos estacionarios y cargados eléctricamente tiene la misma forma matemática que la ley de la gravitación universal de Newton: la fuerza es proporcional al producto de los cargos, inversamente proporcional a la plaza de la distancia entre ellos, y dirigida a lo largo de la línea recta entre ellos. El Coulomb fuerza que un cargo $q_{1}$ ejerce sobre una carga $q_{2}$ es igual en magnitud a la fuerza que $q_{2}$ ejercitos sobre $q_{1}$ , y apunta en la dirección opuesta exacta. La ley de Coulomb es consecuente con la tercera ley de Newton.

El electromagnetismo trata las fuerzas producidas por campos actuando bajo cargos. La ley de fuerza Lorentz proporciona una expresión para la fuerza sobre un cuerpo cargado que puede conectarse a la segunda ley de Newton para calcular su aceleración. Según la ley de fuerza Lorentz, un cuerpo cargado en un campo eléctrico experimenta una fuerza en la dirección de ese campo, una fuerza proporcional a su carga $q$ y a la fuerza del campo eléctrico. Además, a Moveos cuerpo cargado en un campo magnético experimenta una fuerza que también es proporcional a su carga, en una dirección perpendicular tanto al campo como a la dirección de movimiento del cuerpo. Usando el producto de la cruz vectorial,

{displaystyle {vec {F}}=q{vec {E}}+q{vec {v}}times {vec {B}}.}

La ley de fuerza de Lorentz en vigor: los electrones están doblados en una trayectoria circular por un campo magnético.

Si el campo eléctrico desaparece ( ${vec {E}}=0$ ), entonces la fuerza será perpendicular al movimiento de la carga, al igual que en el caso de movimiento circular uniforme estudiado anteriormente, y la carga circulará (o más generalmente se mueve en una helix) alrededor de las líneas de campo magnético en la frecuencia de ciclotron ${displaystyle omega =qB/m}$ . La espectrometría masiva funciona aplicando campos eléctricos y/o magnéticos para mover cargas y medir la aceleración resultante, que por la ley de fuerza de Lorentz produce la relación de masa a carga.

Las colecciones de cuerpos cargados no siempre obedecen la tercera ley de Newton: puede haber un cambio en la cantidad de movimiento de un cuerpo sin un cambio compensatorio en la cantidad de movimiento de otro. La discrepancia se explica por el impulso que lleva el propio campo electromagnético. El momento por unidad de volumen del campo electromagnético es proporcional al vector de Poynting.

Existe un sutil conflicto conceptual entre el electromagnetismo y la primera ley de Newton: la teoría del electromagnetismo de Maxwell predice que las ondas electromagnéticas viajarán a través del espacio vacío a una velocidad constante y definida. Por lo tanto, algunos observadores inerciales aparentemente tienen un estatus privilegiado sobre los demás, a saber, aquellos que miden la velocidad de la luz y encuentran que es el valor predicho por las ecuaciones de Maxwell. En otras palabras, la luz proporciona un estándar absoluto para la velocidad, pero el principio de inercia sostiene que no debería haber tal estándar. Esta tensión se resuelve en la teoría de la relatividad especial, que revisa las nociones de espacio y tiempo de tal forma que todos los observadores inerciales coincidirán en la velocidad de la luz en el vacío..

Relatividad especial

En especial relatividad, la regla que Wilczek llamó "La Ley Cero de Newton" se descompone: la masa de un objeto compuesto no es simplemente la suma de las masas de las piezas individuales. La primera ley de Newton, movimiento inercial, sigue siendo verdad. Una forma de la segunda ley de Newton, esa fuerza es la tasa de cambio de impulso, también sostiene, al igual que la conservación del impulso. Sin embargo, la definición de impulso se modifica. Entre las consecuencias de esto está el hecho de que cuanto más rápido se mueve un cuerpo, más difícil es acelerar, y por lo tanto, no importa cuánta fuerza se aplique, un cuerpo no puede ser acelerado a la velocidad de la luz. Dependiendo del problema a la mano, el impulso en la relatividad especial puede ser representado como un vector tridimensional, ${displaystyle {vec {p}}=mgamma {vec {v}}}$ , donde $m$ es la masa de descanso del cuerpo y $gamma$ es el factor Lorentz, que depende de la velocidad del cuerpo. Alternativamente, el impulso y la fuerza pueden ser representados como cuatro vencedores.

La mecánica newtoniana es una buena aproximación a la relatividad especial cuando las velocidades involucradas son pequeñas en comparación con la de la luz.

Relatividad general

La relatividad general es la teoría de la gravedad que va más allá de la de Newton. En la relatividad general, la fuerza gravitatoria se vuelve a imaginar como la curvatura del espacio-tiempo. Una trayectoria curva como una órbita no es el resultado de una fuerza que desvía un cuerpo de una trayectoria ideal en línea recta, sino el intento del cuerpo de caer libremente a través de un fondo que a su vez está curvado por la presencia de otras masas. Una observación de John Archibald Wheeler que se ha vuelto proverbial entre los físicos resume la teoría: 'El espacio-tiempo le dice a la materia cómo moverse; la materia le dice al espacio-tiempo cómo curvarse." El mismo Wheeler pensó en esta relación recíproca como una forma moderna y generalizada de la tercera ley de Newton. La relación entre la distribución de la materia y la curvatura del espacio-tiempo está dada por las ecuaciones de campo de Einstein, que requieren cálculo tensorial para expresarse.

La teoría newtoniana de la gravedad es una buena aproximación a las predicciones de la relatividad general cuando los efectos gravitatorios son débiles y los objetos se mueven lentamente en comparación con la velocidad de la luz.

Mecánica cuántica

La mecánica cuántica es una teoría de la física desarrollada originalmente para comprender los fenómenos microscópicos: el comportamiento a escala de moléculas, átomos o partículas subatómicas. En términos generales y generales, cuanto más pequeño es un sistema, más requerirá un modelo matemático adecuado comprender los efectos cuánticos. El fundamento conceptual de la física cuántica es muy diferente al de la física clásica. En lugar de pensar en cantidades como la posición, el momento y la energía como propiedades que un objeto tiene, uno considera qué resultado podría aparecer cuando se realiza una medición de un tipo elegido. La mecánica cuántica permite al físico calcular la probabilidad de que una medida elegida produzca un resultado particular. El valor esperado de una medida es el promedio de los posibles resultados que podría arrojar, ponderados por sus probabilidades de ocurrencia.

El teorema de Ehrenfest proporciona una conexión entre los valores esperados cuánticos y la segunda ley de Newton, una conexión que es necesariamente inexacta, ya que la física cuántica es fundamentalmente diferente de la clásica. En la física cuántica, la posición y el momento están representados por entidades matemáticas conocidas como operadores hermitianos, y la regla de Born se usa para calcular los valores esperados de una medida de posición o una medida de momento. Estos valores esperados generalmente cambiarán con el tiempo; es decir, dependiendo del momento en que (por ejemplo) se realice una medición de posición, variarán las probabilidades de sus diferentes posibles resultados. El teorema de Ehrenfest dice, en términos generales, que las ecuaciones que describen cómo estos valores esperados cambian con el tiempo tienen una forma que recuerda a la segunda ley de Newton. Sin embargo, cuanto más pronunciados son los efectos cuánticos en una situación dada, más difícil es derivar conclusiones significativas de esta semejanza.

Historia

Isaac Newton (1643-1727), en un retrato de Godfrey Kneller de 1689
La propia copia de Newton de su Principia, con correcciones escritas a mano para la segunda edición, en la Biblioteca Wren en Trinity College, Cambridge
Las primeras y segundas leyes de Newton, en latín, del original 1687 Principia Mathematica

Los conceptos invocados en las leyes del movimiento de Newton (masa, velocidad, cantidad de movimiento, fuerza) tienen predecesores en trabajos anteriores, y el contenido de la física newtoniana se desarrolló aún más después de la época de Newton. Newton combinó el conocimiento de los movimientos celestes con el estudio de los eventos en la Tierra y demostró que una teoría de la mecánica podía abarcar ambos.

Antecedentes antiguos y medievales

El tema de la física a menudo se remonta a Aristóteles; sin embargo, la historia de los conceptos involucrados está oscurecida por múltiples factores. Una correspondencia exacta entre los conceptos aristotélicos y modernos no es fácil de establecer: Aristóteles no distinguió claramente lo que llamaríamos velocidad y fuerza, y utilizó el mismo término para densidad y viscosidad; concibió el movimiento como siempre a través de un medio, más que a través del espacio. Además, algunos conceptos a menudo denominados "aristotélicos" podría atribuirse mejor a sus seguidores y comentaristas sobre él. Estos comentaristas encontraron que la física aristotélica tenía dificultades para explicar el movimiento de un proyectil. Aristóteles dividió el movimiento en dos tipos: "natural" y "violento". El "natural" el movimiento de la materia sólida terrestre era caer hacia abajo, mientras que un movimiento "violento" movimiento podría empujar un cuerpo hacia los lados. Además, en la física aristotélica, un "violento" el movimiento requiere una causa inmediata; separado de la causa de su "violento" movimiento, un cuerpo volvería a su estado "natural" conducta. Sin embargo, una jabalina continúa moviéndose después de que deja la mano de su lanzador. Aristóteles concluyó que el aire alrededor de la jabalina debe tener la capacidad de mover la jabalina hacia adelante. John Philoponus, un pensador griego bizantino activo durante el siglo VI, encontró esto absurdo: el mismo medio, el aire, era de alguna manera responsable tanto de sostener el movimiento como de impedirlo. Si la idea de Aristóteles fuera cierta, dijo Philoponus, los ejércitos lanzarían armas soplándolas con fuelles. Philoponus argumentó que poner un cuerpo en movimiento impartía una cualidad, un ímpetu, que estaría contenido dentro del propio cuerpo. Mientras se mantuviera su ímpetu, el cuerpo continuaría moviéndose. En los siglos siguientes, personas como Nur ad-Din al-Bitruji, Avicena, Abu'l-Barakāt al-Baghdādī, John Buridan y Alberto de Sajonia presentaron versiones de la teoría del ímpetu. En retrospectiva, la idea de ímpetu puede verse como un precursor del concepto moderno de impulso. (La intuición de que los objetos se mueven de acuerdo con algún tipo de ímpetu persiste en muchos estudiantes de física introductoria).

La inercia y la primera ley

El concepto moderno de inercia se atribuye a Galileo. Sobre la base de sus experimentos, Galileo concluyó que el "natural" el comportamiento de un cuerpo en movimiento era seguir moviéndose, hasta que algo interfiriera con él. Galileo reconoció que en el movimiento de un proyectil, la gravedad de la Tierra afecta el movimiento vertical pero no el horizontal. Sin embargo, la idea de inercia de Galileo no era exactamente la que sería codificada en la primera ley de Newton. Galileo pensó que un cuerpo que se desplazara inercialmente una gran distancia seguiría la curvatura de la Tierra. Esta idea fue corregida por Isaac Beeckman, René Descartes y Pierre Gassendi, quienes reconocieron que el movimiento de inercia debería ser un movimiento en línea recta.

La fuerza y la segunda ley

Christiaan Huygens, en su Horologium Oscillatorium (1673), planteó la hipótesis de que "Por la acción de la gravedad, cualquiera que sea su fuente, sucede que los cuerpos son movidos por un movimiento compuesto tanto de un movimiento uniforme en una dirección u otra como de un movimiento hacia abajo debido a la gravedad." La segunda ley de Newton generalizó esta hipótesis de la gravedad a todas las fuerzas.

Una característica importante de la física newtoniana es que las fuerzas pueden actuar a distancia sin necesidad de contacto físico. Por ejemplo, el Sol y la Tierra se atraen gravitacionalmente, a pesar de estar separados por millones de kilómetros. Esto contrasta con la idea, defendida por Descartes entre otros, de que la gravedad del Sol mantenía a los planetas en órbita haciéndolos girar en un vórtice de materia transparente, éter. Newton consideró explicaciones etéreas de la fuerza, pero finalmente las rechazó. El estudio del magnetismo por parte de William Gilbert y otros creó un precedente para pensar en fuerzas inmateriales, e incapaz de encontrar una explicación cuantitativamente satisfactoria de su ley de la gravedad en términos de un modelo etéreo, declaró finalmente Newton, & #34;No finjo ninguna hipótesis": si se podría o no encontrar un modelo como los vórtices de Descartes para sustentar las teorías del movimiento y la gravedad de los Principia, la primera Los motivos para juzgarlos deben ser las predicciones exitosas que hicieron. Y, de hecho, desde la época de Newton todos los intentos de tal modelo han fracasado.

Conservación de la cantidad de movimiento y la tercera ley

Johannes Kepler sugirió que las atracciones gravitatorias eran recíprocas (que, por ejemplo, la Luna atrae a la Tierra mientras que la Tierra atrae a la Luna), pero no argumentó que tales pares sean iguales y opuestos. En sus Principios de filosofía (1644), Descartes introdujo la idea de que durante una colisión entre cuerpos, una "cantidad de movimiento" permanece sin cambios. Descartes definió esta cantidad de forma algo imprecisa sumando los productos de la velocidad y el "tamaño" de cada cuerpo, donde "tamaño" para él incorporó tanto volumen como superficie. Además, Descartes pensó en el universo como un pleno, es decir, lleno de materia, por lo que todo movimiento requería que un cuerpo desplazara un medio a medida que se movía. Durante la década de 1650, Huygens estudió las colisiones entre esferas duras y dedujo un principio que ahora se identifica como la conservación del momento. Christopher Wren más tarde deduciría las mismas reglas para las colisiones elásticas que tenía Huygens, y John Wallis aplicaría la conservación del momento para estudiar las colisiones inelásticas. Newton citó el trabajo de Huygens, Wren y Wallis para apoyar la validez de su tercera ley.

Newton llegó a su conjunto de tres leyes de forma incremental. En un manuscrito de 1684 escrito a Huygens, enumeró cuatro leyes: el principio de inercia, el cambio de movimiento por la fuerza, una declaración sobre el movimiento relativo que hoy se llamaría invariancia de Galileo y la regla de que las interacciones entre cuerpos no cambian el movimiento. de su centro de masa. En un manuscrito posterior, Newton agregó una ley de acción y reacción, mientras decía que esta ley y la ley del centro de masa se implicaban mutuamente. Newton probablemente se decidió por la presentación en los Principia, con tres leyes primarias y luego otras declaraciones reducidas a corolarios, durante 1685.

Después de los Principios

Página 157 de Mecanismo de los Cielos (1831), la versión ampliada de Mary Somerville de los dos primeros volúmenes de Laplace Traité de mécanique céleste. Aquí, Somerville deduce la inversa ley de gravedad de las leyes de Kepler de movimiento planetario.

Newton expresó su segunda ley diciendo que la fuerza sobre un cuerpo es proporcional a su cambio de movimiento, o impulso. Para cuando escribió el Principia, ya había desarrollado el cálculo (que llamó "la ciencia de las fluxiones"), pero en el Principia no hizo uso explícito de ella, tal vez porque creía que los argumentos geométricos en la tradición de Euclid eran más rigurosos. En consecuencia, el Principia no expresa la aceleración como el segundo derivado de la posición, y por lo tanto no da la segunda ley como $F=ma$ . Esta forma de la segunda ley fue escrita (para el caso especial de fuerza constante) al menos hasta 1716, por Jakob Hermann; Leonhard Euler la emplearía como premisa básica en la década de 1740. Euler fue pionero en el estudio de cuerpos rígidos y estableció la teoría básica de la dinámica del fluido. Pierre-Simon Laplace tiene cinco volúmenes Traité de mécanique céleste (1798-1825) forsook geometry y desarrollado mecánica puramente a través de expresiones algebraicas, al tiempo que resuelve preguntas que la Principia había dejado abierta, como una teoría completa de las mareas.

El concepto de energía se convirtió en una parte clave de la mecánica newtoniana en el período posterior a Newton. Huygens' La solución de la colisión de esferas duras mostró que en ese caso, no solo se conserva el momento, sino también la energía cinética (o, más bien, una cantidad que en retrospectiva podemos identificar como la mitad de la energía cinética total). La cuestión de qué se conserva durante todos los demás procesos, como las colisiones inelásticas y el movimiento ralentizado por la fricción, no se resolvió hasta el siglo XIX. Los debates sobre este tema se superpusieron con disputas filosóficas entre los puntos de vista metafísicos de Newton y Leibniz, y variantes del término "fuerza" a veces se usaban para denotar lo que llamaríamos tipos de energía. Por ejemplo, en 1742, Émilie du Châtelet escribió: "La fuerza muerta consiste en una simple tendencia al movimiento: tal es la de un resorte listo para relajarse; fuerza viva es la que tiene un cuerpo cuando está en movimiento real." En terminología moderna, "fuerza muerta" y "fuerza viva" corresponden a energía potencial y energía cinética respectivamente. La conservación de la energía no se estableció como un principio universal hasta que se entendió que la energía del trabajo mecánico puede disiparse en calor. Con el concepto de energía dado una base sólida, las leyes de Newton podrían derivarse dentro de formulaciones de la mecánica clásica que ponen la energía en primer lugar, como en las formulaciones de Lagrangian y Hamilton descritas anteriormente.

Las presentaciones modernas de las leyes de Newton utilizan las matemáticas de los vectores, un tema que no se desarrolló hasta finales del siglo XIX y principios del XX. El álgebra vectorial, iniciada por Josiah Willard Gibbs y Oliver Heaviside, surgió y suplantó en gran medida al anterior sistema de cuaterniones inventado por William Rowan Hamilton.

Contenido relacionado

Más resultados...