Johnson sólido

La gyrobicupola cuadrada alargadaJ₃₇), un sólido Johnson

Este ejemplo de 24 triángulo equilátero no es un sólido de Johnson porque no es convexo.

Este ejemplo de 24 plazas no es un sólido de Johnson porque no es estrictamente convexo (tiene ángulos dihedral de 180°).

En geometría, un sólido de Johnson es un poliedro estrictamente convexo cuya cara es un polígono regular. No hay ningún requisito de que cada cara deba ser el mismo polígono, o que los mismos polígonos se unan alrededor de cada vértice. Un ejemplo de un sólido de Johnson es la pirámide de base cuadrada con lados equiláteros (J1); tiene 1 cara cuadrada y 4 caras triangulares. Algunos autores exigen que el sólido no sea uniforme (es decir, que no sea un sólido platónico, un sólido de Arquímedes, un prisma uniforme o un antiprisma uniforme) antes de referirse a él como un "sólido de Johnson".

Como en cualquier sólido estrictamente convexo, al menos tres caras se encuentran en cada vértice, y el total de sus ángulos es menor a 360 grados. Dado que un polígono regular tiene ángulos de al menos 60 grados, se deduce que como máximo cinco caras se encuentran en cualquier vértice. La pirámide pentagonal (J₂) es un ejemplo que tiene un vértice de grado 5.

Aunque no existe una restricción obvia de que cualquier polígono regular dado no pueda ser una cara de un sólido de Johnson, resulta que las caras de los sólidos de Johnson que no son uniformes (es decir, no son un sólido platónico, un sólido de Arquímedes, un prisma uniforme, o antiprisma uniforme) siempre tienen 3, 4, 5, 6, 8 o 10 lados.

En 1966, Norman Johnson publicó una lista que incluía los 92 sólidos de Johnson (excluyendo los 5 sólidos platónicos, los 13 sólidos de Arquímedes, los infinitos prismas uniformes y los infinitos antiprismas uniformes), y les dio sus nombres y números.. No probó que solo había 92, pero sí conjeturó que no había otros. Victor Zalgaller en 1969 demostró que la lista de Johnson estaba completa.

De los sólidos de Johnson, la girobicúpula cuadrada alargada (J₃₇), también llamada pseudorombicuboctaedro, es única en ser localmente uniforme de vértice: hay 4 caras en cada vértice, y su disposición es siempre la misma: 3 cuadrados y 1 triángulo. Sin embargo, no es de vértice transitivo, ya que tiene diferente isometría en diferentes vértices, lo que lo convierte en un sólido de Johnson en lugar de un sólido de Arquímedes.

Nombres

La denominación de los sólidos de Johnson sigue una fórmula descriptiva flexible y precisa, de modo que muchos sólidos se pueden nombrar de diferentes maneras sin comprometer su precisión como descripción. La mayoría de los sólidos de Johnson se pueden construir a partir de los primeros (pirámides, cúpulas y rotondas), junto con los sólidos, prismas y antiprismas platónicos y de Arquímedes; el centro del nombre de un sólido en particular reflejará estos ingredientes. A partir de ahí, se añaden a la palabra una serie de prefijos para indicar adiciones, rotaciones y transformaciones:

• Bi-[ceder] indica que se unen dos copias del sólido en cuestión. Para la cúpula y las rotundas, los sólidos se pueden unir para que o bien como caras (ortho...) o caras diferentes (gyro-[*]Nos vemos. Usando esta nomenclatura, un octaedro se puede describir como un bipirámide cuadrado[4], un cuboctaedro como gyrobicupola triangular[3cc*], y un icosidodecahedro como pentagonal gyrobirotunda[5rr*].
• Elongated[=] indica que un prisma se une a la base del sólido en cuestión, o entre las bases en el caso de los sólidos Bi-. Un rhombicuboctaedro se puede describir como un ortobicupola cuadrada.
• Gyroelongated[z] indica que un antiprisma se une a la base del sólido en cuestión o entre las bases en el caso de sólidos Bi-. Un icosahedro puede describirse como bipyramid pentagonal.
• Aumentado[+] indica otro poliedro, a saber, una pirámide o cúpula, se une a una o más caras del sólido en cuestión.
• Diminished[-] indica que una pirámide o cúpula se elimina de una o más caras del sólido en cuestión.
• Gyrate[*] indica que una cúpula montada en o ofrecida en el sólido en cuestión es rotada de tal manera que los diferentes bordes coinciden, como en la diferencia entre orto- y girobicupolae.

Las últimas tres operaciones (aumento, disminución y giro) se pueden realizar varias veces para ciertos sólidos grandes. Bi- &amperio; Tri- indican una operación doble y triple respectivamente. Por ejemplo, un sólido bigyrate tiene dos cúpulas giradas, y un sólido tridisminuido tiene tres pirámides o cúpulas eliminadas.

En ciertos sólidos grandes, se hace una distinción entre sólidos donde las caras alteradas son paralelas y sólidos donde las caras alteradas son oblicuas. Para- indica el primero, que el sólido en cuestión tiene caras paralelas alteradas, y meta- el segundo, caras oblicuas alteradas. Por ejemplo, un sólido parabiaugmentado tiene dos caras paralelas aumentadas, y un sólido metabigirado tiene 2 caras oblicuas giradas.

Los últimos sólidos de Johnson tienen nombres basados en ciertos complejos de polígonos a partir de los cuales se ensamblan. Estos nombres son definidos por Johnson con la siguiente nomenclatura:

• A lune es un complejo de dos triángulos unidos a los lados opuestos de un cuadrado.
• Spheno- indica un complejo tipo cuñada formado por dos lunes adyacentes. Dispheno... indica dos complejos.
• Hebespheno- indica un complejo contundente de dos lunes separado por una tercera luna.
• Corona es un complejo coronario de ocho triángulos.
• Megacorona es un complejo coronario más grande de 12 triángulos.
• El sufijo -cingulo indica un cinturón de 12 triángulos.

Enumeración

Pirámides, cúpulas y rotonda

Los primeros 6 sólidos de Johnson son pirámides, cúpulas o rotondas con un máximo de 5 caras laterales. Las pirámides y cúpulas con 6 o más caras laterales son coplanares y, por lo tanto, no son sólidos de Johnson.

Pirámides

Los dos primeros sólidos de Johnson, J1 y J2, son pirámides. La pirámide triangular es el tetraedro regular, por lo que no es un sólido de Johnson. Representan secciones de poliedros regulares.

Regular 3 T	J1 4 título	J2 5 titulado
pirámide triangular (Tetraedro)	pirámide cuadrada	pirámide pentagonal
Related regular polyhedra
Tetraedro	Octahedron	Icosahedron

Cúpulas y rotonda

Los siguientes cuatro sólidos de Johnson son tres cúpulas y una rotonda. Representan secciones de poliedros uniformes.

Cupola				Rotunda
Uniforme uniforme	J3 3c aC-	J4 4c	J5 5c	J6 5r aD-
Fastigio (Cenola de la Digonal) (Prismo triangular)	Triangular cupola	Copa cuadrado	Cupola pentagonal	Pentagonal rotunda
Related uniform polyhedra
	Cuboctahedron	Rhombicuboctahedron	Rhombicosidodecahedron	Icosidodecahedron

Pirámides modificadas

Los sólidos de Johnson 7 a 17 se derivan de pirámides.

Pirámides alargadas y giroalargadas

En la pirámide triangular giroelongada, tres pares de triángulos adyacentes son coplanares y forman rombos no cuadrados, por lo que no es un sólido de Johnson.

Pirámides alargadas			Pirámides Gyroelongated
J7 3=	J8 4=año	J9 5=año	Coplanar	J10 4z	J11 5z titulado Yo...
pirámide triangular alargada	pirámide cuadrada	pirámide pentagonal alargada	pirámide triangular (diminished trigonal trapezohedron)	pirámide cuadrada	Pirámide pentagonal
Aumentado de polihedra
tetrahedron prisma triangular	pirámide cuadrada cube	pirámide pentagonal prisma pentagonal	tetrahedron octaedro	pirámide cuadrada antiprisma cuadrado	pirámide pentagonal antiprismos pentagonal

Bipirámides

La bipirámide cuadrada es el octaedro regular, mientras que la bipirámide pentagonal giroalargada es el icosaedro regular, por lo que no son sólidos de Johnson. En la bipirámide triangular giroelongada, seis pares de triángulos adyacentes son coplanares y forman rombos no cuadrados, por lo que tampoco es un sólido de Johnson.

Bipyramids			Bipirámides alargadas			Bipirámides Gyroelongated
J12 3 contactos	Recursos ordinarios	J13 5 contactos	J14 3 = título	J15 4 =	J16 5 = título	Coplanar	J17 4 fielz	Recursos ordinarios
Bipirámide triangular	Bipyramid cuadrado (octaedro)	Bipirámide pentagonal	Bipyramid triangular alargada	Bipyramid cuadrado alargado	Bipyramid pentagonal alargado	Bipyramid triangular Gyroelongated (trigonal trapezohedron)	Bipirámide cuadrado	Bipyramid pentagonal Gyroelongated (icosahedron)
Aumentado de polihedra
tetrahedron	pirámide cuadrada	pirámide pentagonal	tetrahedron prisma triangular	pirámide cuadrada cube	pirámide pentagonal prisma pentagonal	tetrahedron Octahedron	pirámide cuadrada antiprisma cuadrado	pirámide pentagonal antiprismos pentagonal

Cúpulas y rotondas modificadas

Los sólidos de Johnson 18 a 48 se derivan de cúpulas y rotondas.

Cúpulas y rotondas alargadas y giroalargadas

Elongated cupola				Elongated rotunda	Cupola Gyroelongated				Gyroelongated rotunda
Coplanar	J18 3c=	J19 4c= eC-	J20 5c=	J21 5r=	Concave	J22 3cz	J23 4cz	J24 5cz	J25 5rz
Elongated fastigium	Copa triangular alargada	Elongated square cupola	Elongated pentagonal cupola	Elongated pentagonal rotunda	Fastigium Gyroelongated	Cupola triangular a lo largo	Armola cuadrada	Gloola pentagonal de Gyroelongated	Gyroelongated pentagonal rotunda
Aumentado de polihedra
Prisma cuadrada Triangular prism	Prisma hexagonal Triangular cupola	El prisma octogonal Copa cuadrado	Prisma Decagonal Cupola pentagonal	Prisma Decagonal Pentagonal rotunda	antiprisma cuadrado Triangular prism	Antiprisma hexagonal Triangular cupola	Antiprisma Octagonal Copa cuadrado	Antiprisma Decagonal Cupola pentagonal	Antiprisma Decagonal Pentagonal rotunda

Bicúpulas

La girobicúpula triangular es un sólido de Arquímedes (en este caso, el cuboctaedro), por lo que no es un sólido de Johnson.

Ortobicupola				Gyrobicupola
Coplanar	J27 3cc	J28 4cc	J30 5cc	J26 2cc*	Semiregular	J29 4cc*	J31 5cc*
Orthobifastigium	Triangular orthobicupola	Square orthobicupola	Pentagonal orthobicupola	Gyrobifastigium	Triangular gyrobicupola (cuboctaedro)	Gyrobicupola cuadrado	Girobicupola pentagonal
Aumentado de poliedro
Triangular prism	Triangular cupola	Copa cuadrado	Cupola pentagonal	Triangular prism	Triangular cupola	Copa cuadrado	Cupola pentagonal

Cúpulas-rotondas y birotondas

La girobirotonda pentagonal es un sólido de Arquímedes (en este caso, el icosidodecaedro), por lo que no es un sólido de Johnson.

Cupola-rotunda		Birotunda
J32 5cr	J33 5cr*	J34 5rr aD*	Semiregular
Pentagonal orthocupolarotunda	Girocupolarotunda pentagonal	Pentagonal orthobirotunda	Girobirotunda pentagonal (icosidodecahedron)
Aumentado de polihedra
Cupola pentagonal Pentagonal rotunda		Pentagonal rotunda

Bicúpulas alargadas

La ortobicúpula cuadrada alargada es un sólido de Arquímedes (en este caso, el rombicuboctaedro), por lo que no es un sólido de Johnson.

Elongated orthobicupola				Gyrobicupola alargada
Coplanar	J35 3c=c	Semiregular	J38 5c=c	Coplanar	J36 3c=c*	J37 4c=c* eC*	J39 5c=c*
Ortobifastigio alargado	Ortobicupola triangular alargada	Ortobicupola cuadrada (rhombicuboctahedron)	Elongated pentagonal orthobicupola	Elongated gyrobifastigium	Gyrobicupola triangular alargada	Girobicupola cuadrada alargada	Gyrobicupola pentagonal alargado
Aumentado de polihedra
Prisma cuadrada Triangular prism	Prisma hexagonal Triangular cupola	El prisma octogonal Copa cuadrado	Prisma Decagonal Cupola pentagonal	Prisma cuadrada Triangular prism	Prisma hexagonal Triangular cupola	El prisma octogonal Copa cuadrado	Prisma Decagonal Cupola pentagonal

Cúpulas-rotondas y birotondas alargadas

Elongated cupola-rotunda		Birotunda alargada
J40 5c=r	J41 5c=r*	J42 5r=r	J43 5r=r*
Ortocupolarotunda pentagonal	Gyrocupolarotunda pentagonal alargado	Elongated pentagonal orthobirotunda	Gyrobirotunda pentagonal alargada
Aumentado de polihedra
Prisma Decagonal Cupola pentagonal Pentagonal rotunda		Prisma Decagonal Pentagonal rotunda

Bicúpulas, cúpulas-rotondas y bicúpulas giroelongadas

Estos sólidos de Johnson tienen 2 formas quirales.

Bicupola Gyroelongated				Gyroelongated cupola-rotunda	Gyroelongated birotunda
Concave	J44 3czc	J45 4czc	J46 5czc	J47 5czr	J48 5rzr
Bifastigio Gyroelongated	Bicupola triangular	Bicupola cuadrada	Gyroelongated pentagonal bicupola	Gloolarotunda pentagonal de Gyroelongated	Birotunda pentagonal Gyroelongated
Aumentado de polihedra
Triangular prism Antiprisma cuadrado	Triangular cupola Antiprisma hexagonal	Copa cuadrado Antiprisma Octagonal	Cupola pentagonal Antiprisma Decagonal	Cupola pentagonal Pentagonal rotunda Antiprisma Decagonal	Pentagonal rotunda Antiprisma Decagonal

Prismas aumentados

Los sólidos de Johnson 49 a 57 se construyen aumentando los lados de los prismas con pirámides cuadradas.

Prismas triangulares aumentados			Prismos pentagonales aumentados		Prismas hexagonales aumentados
J49 3=+	J50 3=+	J51 3=++	J52 5=+	J53 5=+	J54 6=+	J55 6=+	J56 6=+x	J57 6=++
Prisma triangular aumentada	El prisma triangular biaugmentado	Triaugmented triangular prism	Prismo pentagonal aumentado	prisma pentagonal biaugmentado	Prismo hexagonal aumentado	Prisma hexagonal parabiaugmentada	Metabiaugmentado prisma hexagonal	Prisma hexagonal triaugmentada
Aumentado de polihedra
Triangular prism pirámide cuadrada			Prisma pentagonal pirámide cuadrada		Prisma hexagonal pirámide cuadrada

J8 y J15 también encajarían aquí, como un prisma cuadrado aumentado y un prisma cuadrado biaumentado.

Sólidos platónicos modificados

Los sólidos de Johnson 58 a 64 se construyen aumentando o disminuyendo los sólidos platónicos.

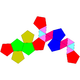
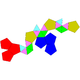
Dodecaedro aumentado

J58 D+	J59 D++	J60 D+x	J61 D+++
Dodecaedro aumentado	Parabiaugmented dodecahedron	Metabiaugmentado dodecahedron	Triaugmented dodecahedron
Aumentado de polihedra
Dodecahedron y pirámide pentagonal

Icosaedros disminuidos disminuidos y aumentados

Diminished icosahedron				Tridiminished icosahedron
J11 (Repetida)	Uniforme uniforme	J62 I-/	J63 I...	J64 I...-+
Diminished icosahedron (pirámide pentagonal a lo largo de la garganta)	Parabidiminished icosahedron (Pentagonal antiprism)	Metabidiminished icosahedron	Tridiminished icosahedron	Tridiminished icosahedron

Sólidos de Arquímedes modificados

Los sólidos de Johnson 65 a 83 se construyen aumentando, disminuyendo o girando sólidos de Arquímedes.

Sólidos de Arquímedes aumentados

Tetraedro truncado aumentado	Cubos truncados aumentados		Aumentado truncado dodecahedra
J65 tT+	J66 tC+	J67 tC++	J68 tD+	J69 tD++	J70 tD+x	J71 tD+++
Tetraedro truncado aumentado	Cubo truncado aumentado	Cube biaugmentado truncado	Aumentado truncado dodecahedron	Parabiaugmentado truncated dodecahedron	Metabiaugmentado truncado dodecahedron	Triaugmented truncated dodecahedron
Aumentado de polihedra
truncated tetrahedron cúpula triangular	truncado cubo cúpula cuadrada		truncado dodecahedron cúpula pentagonal

Girato y rombicosidodecaedros disminuidos

Gyrate rhombicosidodecahedra
J72 eD*	J73 eD**	J74 eD* '	J75 eD***
Gyrate rhombicosidodecahedron	Parabigyrate rhombicosidodecahedron	Metabigyrate rhombicosidodecahedron	Trigyrate rhombicosidodecahedron
Diminished rhombicosidodecahedra
J76 eD-	J80 eD...	J81 eD-/	J83 eD...
Diminished rhombicosidodecahedron	Parabidiminished rhombicosidodecahedron	Metabidiminished rhombicosidodecahedron	Tridiminished rhombicosidodecahedron
Gyrate disminuido rhombicosidodecahedra
J77 –*	J78 - '	J79**	J82*
Paragirate disminuido rhombicosidodecahedron	Metagirate disminuido rhombicosidodecahedron	Bigyrate disminuido rhombicosidodecahedron	Gyrate bidiminished rhombicosidodecahedron

J37 también aparecería aquí como un duplicado (es un rombicuboctaedro giratorio).

Otros sólidos de Arquímedes disminuidos y girados

Otros sólidos de Arquímedes se pueden girar y disminuir, pero todos dan como resultado sólidos previamente contados.

J27	J3	J34	J6	J37	J19	Uniforme uniforme
Gyrate cuboctahedron (triangular orthobicupola)	Diminished cuboctahedron (Golola triangular)	Gyrate icosidodecahedron (Ortoboirotunda pentagonal)	Diminished icosidodecahedron (Rotunda pentagonal)	Gyrate rhombicuboctahedron (Gyrobicupola cuadrada)	Diminished rhombicuboctahedron (elongated square cupola)	Bidiminished rhombicuboctahedron (prismo octogonal)
Gyrated or diminished from polyhedra
Cuboctahedron		Icosidodecahedron		Rhombicuboctahedron

Sólidos elementales

Los sólidos de Johnson 84 a 92 no se derivan de "cortar y pegar" manipulación de sólidos uniformes.

Antiprismas desairadas

Los antiprismas chatos se pueden construir como una alternancia de un antiprisma truncado. Las girobianticúpulas son otra construcción de los antiprismas chatos. Solo se pueden construir antiprismas chatos con un máximo de 4 lados a partir de polígonos regulares. El antiprisma triangular chato es el icosaedro regular, por lo que no es un sólido de Johnson.

J84	Recursos ordinarios	J85
Snub disphenoid ss{2,4}	Icosahedron ss{2,6}	Snub cuadrado antiprisma ss{2,8}
Girobianticupola digonal	Triangular gyrobianticupola	Gyrobianticupola cuadrado

Otros

J86	J87	J88
Sphenocorona	Esphenocorona aumentada	Sphenomegacorona
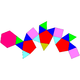
J89	J90	J91	J92
Hebesphenomegacorona	Disphenocingulum	Bilunabirotunda	Hebesfenorotunda triangular

Clasificación por tipos de rostros

Sólidos de Johnson con caras triangulares

Cinco sólidos de Johnson son deltaedros, con todas las caras de triángulos equiláteros:

Sólidos Johnson triangulares y de caras cuadradas

Veinticuatro sólidos de Johnson tienen solo caras triangulares o cuadradas:

Sólidos de Johnson con caras de triángulos y pentágonos

Once sólidos de Johnson solo tienen caras de triángulos y pentágonos:

Sólidos de Johnson triangulares, cuadrados y pentágonos

Veinte sólidos de Johnson solo tienen caras de triángulo, cuadrado y pentágono:

Sólidos de Johnson triangulares, cuadrados y hexagonales

Ocho sólidos de Johnson solo tienen caras triangulares, cuadradas y hexagonales:

Sólidos de Johnson triangulares, cuadrados y octogonales

Cinco sólidos de Johnson solo tienen caras triangulares, cuadradas y octagonales:

Sólidos de Johnson con caras de triángulo, pentágono y decágono

Dos sólidos de Johnson solo tienen caras de triángulo, pentágono y decágono:

Sólidos de Johnson triangulares, cuadrados, pentágonos y hexagonales

Solo un sólido de Johnson tiene caras de triángulo, cuadrado, pentágono y hexágono:

Sólidos de Johnson con caras de triángulo, cuadrado, pentágono y decágono

Dieciséis sólidos de Johnson solo tienen caras de triángulo, cuadrado, pentágono y decágono:

Sólidos de Johnson circunscribibles

25 de los sólidos de Johnson tienen vértices que existen en la superficie de una esfera: 1–6,11,19,27,34,37,62,63,72–83. Todos ellos pueden verse relacionados con un poliedro regular o uniforme por giro, disminución o disección.

Octahedron	Cuboctahedron		Rhombicuboctahedron
J1	J3	J27	J4	J19	J37

Icosahedron				Icosidodecahedron
J2	J11	J62	J63	J6	J34

Rhombicosidodecahedron
J5	J72	J73	J74	J75	J76	J77
	J78	J79	J80	J81	J82	J83