Icosidodecaedro
| Icosidodecahedron | |
|---|---|
 (Haga clic aquí para el modelo giratorio) | |
| Tipo | Arquitecto sólido Uniform polyhedron |
| Elementos | F = 32, E = 60, V = 30 (χ = 2) |
| Caras por lados | 20{3}+12{5} |
| Notación de Conway | aD |
| Símbolos de Schläfli | r{5,3} |
| t1{5,3} | |
| Signatura Wythoff | 2 Silencio 3 5 |
| Coxeter diagrama |     |
| Grupo de Symmetry | Ih, H3, [5,3], (*532), orden 120 |
| Grupo de rotación | I, [5,3]+, (532), orden 60 |
| Ángulo Dihedral | 142.62° #− − 1 ()− − 115()5+25)){displaystyle cos ^{-1}left(-{sqrt {{frac {1}{15}}left(5+2{sqrt {5}right)}}right)} |
| Referencias | U24, C28, W12 |
| Propiedades | Semiregular convex quasiregular |
 Caras de colores |  3.5.3.5 (Vertex figure) |
 Triacontahedron Rhombic (poliedro dual) |  Cifras netas |
En geometría, un icosidodecaedro es un poliedro de veinte (icosi) caras triangulares y doce (dodeca) caras pentagonales. Un icosidodecaedro tiene 30 vértices idénticos, con dos triángulos y dos pentágonos que se encuentran en cada uno, y 60 aristas idénticas, cada una de las cuales separa un triángulo de un pentágono. Como tal, es uno de los sólidos de Arquímedes y, más particularmente, un poliedro cuasiregular.
Geometría
Un icosidodecaedro tiene simetría icosaédrica, y su primera estelación es el compuesto de un dodecaedro y su icosaedro dual, con los vértices del icosidodecaedro ubicados en los puntos medios de los bordes de cualquiera.
Su poliedro dual es el triacontaedro rómbico. Un icosidodecaedro se puede dividir a lo largo de cualquiera de los seis planos para formar un par de rotondas pentagonales, que pertenecen a los sólidos de Johnson.
El icosidodecaedro puede considerarse una girorotonda pentagonal, como una combinación de dos rotondas (compárese con la ortobirotonda pentagonal, uno de los sólidos de Johnson). De esta forma su simetría es D5d, [10,2+], (2*5), orden 20.
La figura de estructura de alambre del icosidodecaedro consiste en seis decágonos regulares planos, que se unen en pares en cada uno de los 30 vértices.
El icosidodecaedro tiene 6 decágonos centrales. Proyectados en una esfera, definen 6 grandes círculos. Buckminster Fuller usó estos 6 grandes círculos, junto con otros 15 y 10 en otros dos poliedros para definir sus 31 grandes círculos del icosaedro esférico.
Coordenadas cartesianas
Las coordenadas cartesianas convenientes para los vértices de un icosidodecaedro con aristas unitarias están dadas por las permutaciones pares de:
- (0, 0, ±φ)
- (±1/2±φ/2±φ2/2)
donde φ es la proporción áurea, 1 + √ 5/2.
El radio mayor (del centro al vértice) del icosidodecaedro está en proporción áurea con respecto a la longitud de sus aristas; por lo tanto, su radio es φ si la longitud de su borde es 1, y su longitud de borde es 1/φ si su radio es 1. Solo unos pocos uniformes Los politopos tienen esta propiedad, incluido el de 600 celdas de cuatro dimensiones, el icosidodecaedro tridimensional y el decágono bidimensional. (El icosidodecaedro es la sección transversal ecuatorial del icosidodecaedro de 600 celdas, y el decágono es la sección transversal ecuatorial del icosidodecaedro). se encuentran en el centro, cada uno contribuyendo con dos radios y un borde.
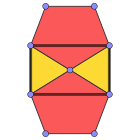
Proyecciones ortogonales
El icosidodecaedro tiene cuatro proyecciones ortogonales especiales, centradas en un vértice, una arista, una cara triangular y una cara pentagonal. Los dos últimos corresponden a los planos A2 y H2 de Coxeter.
| Centrado por | Vertex | Edge | Cara Triángulo | Cara Pentágono |
|---|---|---|---|---|
| Sólido |  |  |  | |
| Wireframe |  |  |  |  |
| Projective simetría | [2] | [2] | [6] | [10] |
| Doble |  |  |  |  |
Superficie y volumen
El área superficial A y el volumen V del icosidodecaedro de longitud de arista a son:
- A=()53+353+4φ φ )a2=()53+325+105)a2.. 29.3059828a2V=14+17φ φ 3a3=45+1756a3.. 13.8355259a3.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft}}} {fnMicrosoft} {fnMicrosoft}} {f}}}}}}} {f}f} {cH0} {f}f}}}}}}f} {f}f}f}}}}}}f}}}}f}}}}}f} {f}f}f}f}f}f} {f}f}f}f}f}f}f}b9}}}}f}b9}}}}}}f}f}}}f}f}f}f}}}f}f}f}b9}f}}b9f}}}b9f}b9b9} # {45+17{sqrt {5}} {6}a} {3} 13.8355259a^{3}
Alicatados esféricos
El icosidodecaedro también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.
 |  Pentágono centrado |  Triángulo centrado |
| Proyección ortográfica | Proyecciones estereográficas | |
|---|---|---|
| Proyecciones ortoográficas | ||||
|---|---|---|---|---|
 |  |  | ||
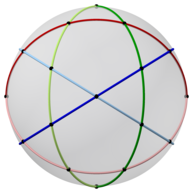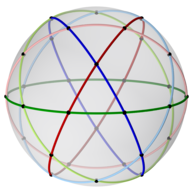| ejes de simetría de 2 veces, 3 veces y 5 veces | ||||
Polítopos relacionados
El icosidodecaedro es un dodecaedro rectificado y también un icosaedro rectificado, que existe como el truncamiento de borde completo entre estos sólidos regulares.
El icosidodecaedro contiene 12 pentágonos del dodecaedro y 20 triángulos del icosaedro:
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Simetría: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| | | | | | |  |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |  |  |  |  |  |  |  |
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
El icosidodecaedro existe en una secuencia de simetrías de poliedros cuasiregulares y mosaicos con configuraciones de vértice (3.n)2, progresando desde mosaicos de la esfera hasta el plano euclidiano y en el plano hiperbólico. Con la simetría de notación orbifold de *n32, todas estas teselaciones son construcciones Wythoff dentro de un dominio fundamental de simetría, con puntos generadores en la esquina del ángulo derecho del dominio.
| * n32 simetrías orbifold de baldosas cuasiregulares: (3.n)2 | |||||||
|---|---|---|---|---|---|---|---|
 Construcción | Spherical | Euclidean | Hiperbólico | ||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |
| Quasiregular cifras |  |  | |  |  |  |  |
| Vertex | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3. |
| *5n2 mutaciones de simetría de los revestimientos cuasiregulares: (5.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simmetría *5n2 [n,5] | Spherical | Hiperbólico | Paracompactar | No | ||||
| *352 [3,5] | *452 [4,5] | *552 [5,5] | *652 [6,5] | *752 [7,5] | *852 [8,5]... | * [∞,5] | [ni,5] | |
| Gráficos | |  |  |  |  |  |  | |
| Config. | (5.3)2 | (5.4)2 | (5.5)2 | (5.6)2 | (5.7)2 | (5.8)2 | (5. | (5.ni)2 |
| Rhombic cifras | |  |  |  | ||||
| Config. | V(5.3)2 | V(5.4)2 | V(5.5)2 | V(5.6)2 | V(5.7)2 | V(5.8)2 | V(5.∞)2 | V(5.∞)2 |
Disección
El icosidodecaedro está relacionado con el sólido de Johnson llamado ortobirotonda pentagonal creado por dos rotondas pentagonales conectadas como imágenes especulares. Por lo tanto, el icosidodecaedro puede denominarse girobirotonda pentagonal con el giro entre las mitades superior e inferior.
 (Disección) |
|
Poliedros relacionados
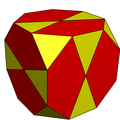
El cubo truncado se puede convertir en un icosidodecaedro dividiendo los octógonos en dos pentágonos y dos triángulos. Tiene simetría piritoédrica.
Ocho poliedros estrella uniformes comparten la misma disposición de vértices. De estos, dos también comparten la misma disposición de aristas: el icosihemidodecaedro pequeño (que tiene las caras triangulares en común) y el dodecahemidodecaedro pequeño (que tiene las caras pentagonales en común). La disposición de los vértices también se comparte con los compuestos de cinco octaedros y de cinco tetrahemihexaedros.
 Icosidodecahedron |  Small icosihemidodecahedron |  Pequeña dodecahemidodecedron |
 Great icosidodecahedron |  Gran dodecahemidodecedron |  Great icosihemidodecahedron |
 Dodecadodecahedron |  Pequeña dodecahemicosahedron |  Gran dodecahemicosahedron |
 Compuesto de cinco octahedra |  Compuesto de cinco tetrahemihexahedra |
Polícora relacionada
En geometría de cuatro dimensiones, el icosidodecaedro aparece en las 600 celdas regulares como la porción ecuatorial que pertenece al primer paso del vértice de las 600 celdas a través del espacio 3D. En otras palabras: los 30 vértices de la celda de 600 que se encuentran a distancias de arco de 90 grados en su hiperesfera circunscrita de un par de vértices opuestos, son los vértices de un icosidodecaedro. La figura de estructura de alambre de la celda 600 consta de 72 decágonos regulares planos. Seis de estos son los decágonos ecuatoriales a un par de vértices opuestos. Son precisamente los seis decágonos los que forman la figura de alambre del icosidodecaedro.
Gráfico de icosidodecaedro
En el campo matemático de la teoría de grafos, un grafo icosidodecaédrico es el gráfico de vértices y aristas del icosidodecaedro, uno de los sólidos de Arquímedes. Tiene 30 vértices y 60 aristas, y es un grafo cuártico grafo de Arquímedes.
Curiosidades
En Star Trek Universe, el juego vulcano de lógica Kal-Toh tiene como objetivo crear un icosidodecaedro holográfico.
En The Wrong Stars, libro uno de la serie Axiom, de Tim Pratt, Elena tiene una máquina de icosidodecaedro a cada lado de ella. [Libro en rústica pág. 336]
La esfera de Hoberman es un icosidodecaedro.
El icosidodecaedro se puede encontrar en todas las células eucariotas, incluidas las células humanas, como formaciones de proteína de cubierta Sec13/31 COPII.
Contenido relacionado
Sistema de coordenadas esféricas
Conjetura de Collatz
Hexadecimal