Icosaedro truncado

Truncated icosahedron
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 32, E = 90, V = 60 (χ = 2)
Caras por lados	12{5}+20{6}
Notación de Conway	tI
Símbolos de Schläfli	t{3,5}
	t0,1{3,5}
Signatura Wythoff	2 5 Silencio 3
Coxeter diagrama
Grupo de Symmetry	Ih, H3, [5,3], (*532), orden 120
Grupo de rotación	I, [5,3]+, (532), orden 60
Ángulo Dihedral	6-6: 138.189685° 6-5: 142,62°
Referencias	U25, C27, W9
Propiedades	Convex semiregular
Caras de colores	5.6.6 (Vertex figure)
Pentakis dodecahedron (poliedro dual)	Cifras netas

En geometría, el icosaedro truncado es un sólido de Arquímedes, uno de los 13 sólidos no prismáticos isogonales convexos cuyas 32 caras son dos o más tipos de polígonos regulares. Es la única de estas formas que no contiene triángulos ni cuadrados. En el uso general, se supone que el grado de truncamiento es uniforme a menos que se especifique lo contrario.

Tiene 12 caras pentagonales regulares, 20 caras hexagonales regulares, 60 vértices y 90 aristas.

Es el poliedro de Goldberg GP_V(1,1) o {5+,3}_1,1, que contiene caras pentagonales y hexagonales.

Esta geometría está asociada con balones de fútbol (balones de fútbol) típicamente estampados con hexágonos blancos y pentágonos negros. Las cúpulas geodésicas, como aquellas cuya arquitectura fue pionera en Buckminster Fuller, a menudo se basan en esta estructura. También corresponde a la geometría de la molécula de fullereno C60 ("buckyball").

Se utiliza en la teselación de relleno de espacio hiperbólica transitiva de células, el panal dodecaédrico de orden 5 bitruncado.

Construcción

Icosahedron

Este poliedro se puede construir a partir de un icosaedro con los 12 vértices truncados (cortados) de manera que un tercio de cada arista se corta en cada uno de los dos extremos. Esto crea 12 nuevas caras de pentágono y deja las 20 caras triangulares originales como hexágonos regulares. Así, la longitud de los bordes es un tercio de la de los bordes originales. Además, la forma tiene 1440 diagonales.

Características

En geometría y teoría de grafos, hay algunas características estándar de poliedro.

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un icosaedro truncado centrado en el origen son permutaciones pares de:

(0, ± 1, ± 3φ)

(±1, ±(2 +φ±2φ)

(±φ± 2, ± 2φ+ 1))

donde φ = 1 + √5/2 es la media dorada. El circunradio es √9φ + 10 ≈ 4.956 y las aristas tienen longitud 2.

Proyecciones ortogonales

El icosaedro truncado tiene cinco proyecciones ortogonales especiales, centradas, en un vértice, en dos tipos de aristas, y dos tipos de caras: hexagonal y pentagonal. Los dos últimos corresponden a los planos A₂ y H₂ de Coxeter.

Proyecciones ortogonales

Centrado por	Vertex	Edge 5-6	Edge 6-6	Cara Hexagon	Cara Pentágono
Sólido
Wireframe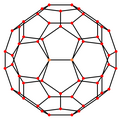
Projective simetría	[2]	[2]	[2]	[6]	[10]
Doble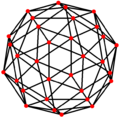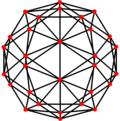

Alicatados esféricos

El icosaedro truncado también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

	Pentágono centrado	hexágono centrado
Proyección ortográfica	Proyecciones estereográficas

Dimensiones

Rectángulos dorados ortogonales en el icosahedro original (antes de cortar)

Si la longitud de la arista de un icosaedro truncado es a, el radio de una esfera circunscrita (una que toca el icosaedro truncado en todos los vértices) es:

ru=a21+9φ φ 2=a458+185.. 2.47801866a{displaystyle r_{mathrm}={frac} {fn} {fn}= {fnK}}= {fnMicroc} {} {fn} {58+18{sqrt {5}}approx} 2.478,018,66a}

donde φ es la proporción áurea.

Este resultado es fácil de obtener utilizando uno de los tres rectángulos áureos ortogonales dibujados en el icosaedro original (antes del corte) como punto de partida para nuestras consideraciones. El ángulo entre los segmentos que unen el centro y los vértices conectados por el borde compartido (calculado sobre la base de esta construcción) es de aproximadamente 23,281446°.

Área y volumen

El área A y el volumen V del icosaedro truncado de longitud de arista a son:

A=()20⋅ ⋅ 323+12⋅ ⋅ 541+25)a2.. 72.607253a2V=125+4354a3.. 55.2877308a3.{displaystyle {begin{aligned}A limit=left(20cdot {frac {3}{2}{sqrt {3}}}}+12cdot {fracfrac} {f}}} {f}}}fncdot {fnfnKf}} {5}{4}} {sqrt {1+{frac {2}{sqrt {5}}}right)a^{2} limiteapprox 72.607,253a^{2}c\c\cH00={125+43{sqrt {}} {4}a} {3} 55.287,7308a^{3}

Con aristas unitarias, el área de la superficie es (redondeada) 21 para los pentágonos y 52 para los hexágonos, juntos 73 (ver áreas de polígonos regulares).

El icosaedro truncado demuestra fácilmente la característica de Euler:

32 + 60 − 90 = 2.

Aplicaciones

Los balones que se usan en el fútbol de asociación y el balonmano en equipo son quizás el ejemplo más conocido de un poliedro esférico análogo al icosaedro truncado que se encuentra en la vida cotidiana. La pelota comprende el mismo patrón de pentágonos regulares y hexágonos regulares, pero es más esférico debido a la presión del aire interior y la elasticidad de la pelota. Este tipo de balón se introdujo en la Copa del Mundo en 1970 (a partir de 2006, este diseño icónico ha sido reemplazado por patrones alternativos).

Las señales de tráfico británicas que indican campos de fútbol utilizan una sección de mosaico hexagonal de color uniforme para representar una pelota de fútbol, en lugar de un icosaedro truncado. Esto enfureció al matemático y comediante Matt Parker, quien inició una petición al gobierno del Reino Unido para cambiar estos signos para que sean geométricamente precisos. La petición fue finalmente rechazada.

Los domos geodésicos generalmente se basan en facetas triangulares de esta geometría con estructuras de ejemplo que se encuentran en todo el mundo, popularizadas por Buckminster Fuller.

Se usó una variación del icosaedro como base de las ruedas de panal (hechas de un material polifundido) usadas por la División de Motores de Pontiac entre 1971 y 1976 en su Trans Am y Grand Prix.

Esta forma también era la configuración de las lentes utilizadas para enfocar las ondas de choque explosivas de los detonadores tanto en el dispositivo como en las bombas atómicas Fat Man.

El icosaedro truncado también se puede describir como un modelo de la molécula Buckminsterfullereno (fullereno) (C₆₀), o "buckyball", un alótropo del carbono elemental, descubierto en 1985. El diámetro de la pelota de fútbol y la molécula de fullereno son de 22 cm y aproximadamente 0,71 nm, respectivamente, por lo que la relación de tamaño es de ≈31 000 000:1.

En la cultura artesanal popular, se pueden hacer bolas brillantes grandes usando un patrón de icosaedro y vasos de plástico, espuma de poliestireno o papel.

En las artes

• Galería
• 

  El icosahedro truncado (izquierda) comparado con un fútbol de asociación.

• 

  Fullerene C₆₀ molécula

• 

  Truncated icosahedral radome en una estación meteorológica

• 

  Truncated icosahedron machined out of 6061-T6 aluminio

• 

  Una obra icosahedron truncada de madera de George W. Hart.

Poliedros relacionados

Family of uniform icosahedral polyhedra
Simetría: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

*n32 mutación simetría de los azulejos truncados: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compacto		Parac.	Hiperbólico no consumado
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncado cifras
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	JUEGO.6	12i.6.6	9i.6.6	6i.6.6
N-kis cifras
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V dieta.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Estos poliedros estelares uniformes y una estelación icosaédrica tienen cascos convexos de icosaedros truncados no uniformes:

Uniform star polyhedra with truncated icosahedra convex hulls
Nonuniform icosahedron truncado 2 5 Silencio 3 U37 2 5/2 Silencio U61 5/2 3 Silencio 5/3 U67 5/3 3 Silencio 2 U73 2 5/3 ()3/2 5/4) Estalación completa Nonuniform icosahedron truncado 2 5 Silencio 3 U38 5/2 5 Silencio 2 U44 5/3 5 latitud 3 U56 2 3 (5/4 5/2Silencio Nonuniform icosahedron truncado 2 5 Silencio 3 U32 Silencio 5/2 3 3

Este poliedro se parece al dodecaedro biselado uniforme que tiene 12 pentágonos, pero 30 hexágonos.

Gráfico icosaédrico truncado

En el campo matemático de la teoría de grafos, un grafo icosaédrico truncado es el gráfico de vértices y aristas del icosaedro truncado, uno de los sólidos de Arquímedes. Tiene 60 vértices y 90 aristas, y es un grafo de Arquímedes cúbico.

Proyección ortográfica

Simetría de 5 veces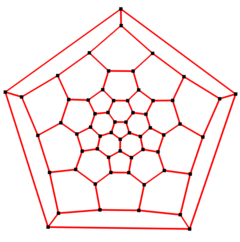

5 veces diagrama de Schlegel

Historia

Piero della La imagen de Francesca de un icosahedro truncado de su libro De quinque corporibus regularibus

El icosaedro truncado fue conocido por Arquímedes, quien clasificó los 13 sólidos de Arquímedes en un trabajo perdido. Todo lo que sabemos de su trabajo sobre estas formas proviene de Pappus de Alejandría, quien simplemente enumera el número de caras para cada una: 12 pentágonos y 20 hexágonos, en el caso del icosaedro truncado. La primera imagen conocida y descripción completa de un icosaedro truncado proviene de un redescubrimiento de Piero della Francesca, en su libro del siglo XV De quinque corporibus regularibus, que incluía cinco de los sólidos de Arquímedes (los cinco truncamientos de los poliedros regulares). La misma forma fue representada por Leonardo da Vinci, en sus ilustraciones para el plagio de Luca Pacioli del libro de della Francesca en 1509. Aunque Albrecht Dürer omitió esta forma de los otros sólidos de Arquímedes enumerados en su libro de 1525 sobre poliedros., Underweysung der Messung, se encontró una descripción del mismo en sus artículos póstumos, publicados en 1538. Más tarde, Johannes Kepler redescubrió la lista completa de los 13 sólidos de Arquímedes, incluido el icosaedro truncado, y los incluyó en su Libro de 1609, Harmonices Mundi.