Hosoedro

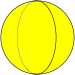
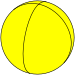
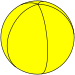
En geometría esférica, un hosoedro n-gonal es un mosaico de lunes sobre una superficie esférica, de modo que cada luna comparte los mismos dos vértices polares opuestos.
A regular n- Hosohedron tiene el símbolo Schläfli {2}n} con cada luno esférico que tiene ángulo interno 2π/nradiantes360/n grados).
Hosoedros como poliedros regulares
Para un poliedro regular cuyo símbolo de Schläfli es {m, n}, el número de caras poligonales es:
- N2=4n2m+2n− − mn.{displaystyle N_{2}={frac {4n}{2m+2n-mn}.}
Los sólidos platónicos conocidos en la antigüedad son las únicas soluciones enteras para m ≥ 3 y n ≥ 3. La restricción m ≥ 3 impone que las caras poligonales deben tener al menos tres lados.
Al considerar los poliedros como mosaicos esféricos, esta restricción se puede relajar, ya que los digones (2 gónos) se pueden representar como lunes esféricos, con un área distinta de cero.
Permitir m = 2 hace
- N2=4n2× × 2+2n− − 2n=n,{displaystyle N_{2}={frac {4n}{2times 2+2n-2n}=n,}
y admite una nueva clase infinita de poliedros regulares, que son los hosoedros. En una superficie esférica, el poliedro {2, n} se representa como n contiguo al lunes, con ángulos interiores de 2π /n. Todos estos lunes esféricos comparten dos vértices comunes.
Simetría caleidoscópica
El 2n{displaystyle 2n} caras de luno esférico digonal de un 2n{displaystyle 2n}- Josohedron, {}2,2n}{displaystyle {2,2n}}, representan los dominios fundamentales de la simetría dihedral en tres dimensiones: la simetría cíclica Cnv{displaystyle C_{nv}, [n]{displaystyle [n]}, ()Alternativa Alternativa nn){displaystyle (*nn)}, orden 2n{displaystyle 2n}. Los dominios de reflexión pueden ser mostrados por lunes de colores alternativos como imágenes de espejo.
Bisecting each lune into two spherical triángulos creates an n{displaystyle n}- bipirámide gonal, que representa la simetría dihedral Dnh{displaystyle D_{nh}, orden 4n{displaystyle 4n}.
Relación con el sólido Steinmetz
El hosoedro tetragonal es topológicamente equivalente al bicilindro sólido de Steinmetz, la intersección de dos cilindros en ángulo recto.
Poliedros derivados
El dual del hosoedro n-gonal {2, n} es el dipedro n-gonal, {n, 2}. El poliedro {2,2} es autodual y es a la vez un hosoedro y un dipedro.
Un hosoedro se puede modificar de la misma manera que los otros poliedros para producir una variación truncada. El hosoedro n-gonal truncado es el prisma n-gonal.
Hosoedro apeirogonal
En el límite, el hosoedro se convierte en un hosoedro apeirogonal como una teselación bidimensional:
Hosótopos
Los análogos multidimensionales en general se denominan hosótopos. Un hosótopo regular con símbolo de Schläfli {2,p,...,q} tiene dos vértices, cada uno con una figura de vértice {p, ...,q}.
El hosótopo bidimensional, {2}, es un digon.
Etimología
El término “hosoedro” parece derivar del griego ὅσος (hosos) “tantos”, siendo la idea que un hosoedro puede tener “tantas caras como deseado”. Fue introducido por Vito Caravelli en el siglo XVIII.
Contenido relacionado
Conjunto vacío
Precisión y exactitud
Historia de la lógica









![{displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)
















![{displaystyle [,,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fa4c06a6c3b5a7bee90e2c44f7530e3f2a46bf8)
![{displaystyle [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa32363c093f4cfd50ecba68068bcfd396ea8bff)
![{displaystyle [3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f671027d56f9c24d65c03a4a26eb0d3b933f4f15)
![{displaystyle [4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d865272ff436d713d5069ae3066bbe07a000a99)
![{displaystyle [5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/958ef87021d704de46ad116821bc677e07d9a5fe)
![{displaystyle [6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/162951515fcb56919dffe17b119f4a0aa7e9dae6)












