Homogeneidad y heterogeneidad (estadísticas)

En estadística, la homogeneidad y su opuesta, la heterogeneidad, surgen al describir las propiedades de un conjunto de datos, o de varios conjuntos de datos. Se relacionan con la validez del supuesto, a menudo conveniente, de que las propiedades estadísticas de cualquier parte de un conjunto de datos general son las mismas que las de cualquier otra parte. En el metanálisis, que combina los datos de varios estudios, la homogeneidad mide las diferencias o similitudes entre los distintos estudios (ver también Heterogeneidad de los estudios).

La homogeneidad se puede estudiar con varios grados de complejidad. Por ejemplo, las consideraciones de homocedasticidad examinan cuánto cambia la variabilidad de los valores de los datos a lo largo de un conjunto de datos. Sin embargo, las cuestiones de homogeneidad se aplican a todos los aspectos de las distribuciones estadísticas, incluido el parámetro de ubicación. Por lo tanto, un estudio más detallado examinaría los cambios en toda la distribución marginal. Un estudio de nivel intermedio podría pasar de observar la variabilidad a estudiar los cambios en la asimetría. Además de éstas, también se aplican cuestiones de homogeneidad a las distribuciones conjuntas.

El concepto de homogeneidad se puede aplicar de muchas maneras diferentes y, para ciertos tipos de análisis estadístico, se utiliza para buscar propiedades adicionales que podrían necesitar ser tratadas como variables dentro de un conjunto de datos una vez que se detectan algunos tipos iniciales de no homogeneidad. han sido tratados.

De varianza

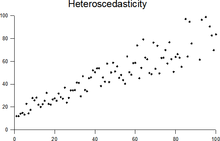
En las estadísticas, una secuencia de variables aleatorias es homoscedastic () si todas sus variables aleatorias tienen la misma varianza finita; esto también se conoce como homogeneidad de la varianza. La noción complementaria se llama heteroscedasticidad, también conocida como heterogeneidad de varianza. Las ortografías homoskedasticity y heterosquedasticidad también se utilizan con frecuencia. Suponiendo que una variable es homoscedastic cuando en realidad es heteroscedastic () resulta en estimaciones de puntos imparciales pero ineficientes y en estimaciones parciales de errores estándar, y puede resultar en sobreestimar la bondad del ajuste como medida por el coeficiente Pearson.

La existencia de heteroscedasticidad es una preocupación importante en el análisis de regresión y el análisis de varianza, ya que invalida las pruebas estadísticas de importancia que suponen que los errores de modelado tienen la misma variabilidad. Mientras que el estimador de los mínimos cuadrados ordinarios todavía es imparcial en la presencia de heteroscedasticidad, es ineficiente e inferencia basada en la asunción de la homoskedasticidad es engañoso. En ese caso, se utilizaron con frecuencia los mínimos cuadrados generalizados (GLS). Hoy en día, la práctica estándar en econometría es incluir errores estándar consistentes en Heteroskedasticidad en lugar de utilizar GLS, ya que GLS puede exhibir sesgos fuertes en pequeñas muestras si se desconoce la función Skedastic real.

Debido a que la heteroscedasticidad se refiere a las expectativas del segundo momento de los errores, su presencia se refiere a la inespección del segundo orden.

El econométrico Robert Engle fue galardonado con el Premio Nobel de Economía de 2003 por sus estudios sobre el análisis de regresión en presencia de heteroscedasticidad, lo que llevó a su formulación de la técnica de modelado de heteroscedasticidad condicional autoregresiva (ARCH).

Ejemplos

Regresión

Las diferencias en los valores típicos en todo el conjunto de datos podrían abordarse inicialmente mediante la construcción de un modelo de regresión utilizando ciertas variables explicativas para relacionar las variaciones en el valor típico con cantidades conocidas. Luego debería haber una etapa posterior de análisis para examinar si los errores en las predicciones de la regresión se comportan de la misma manera en todo el conjunto de datos. Así, la cuestión pasa a ser la de la homogeneidad de la distribución de los residuos, a medida que cambian las variables explicativas. Ver análisis de regresión.

Serie temporal

Las etapas iniciales en el análisis de una serie temporal pueden implicar trazar valores en función del tiempo para examinar la homogeneidad de la serie de varias maneras: estabilidad a lo largo del tiempo en contraposición a una tendencia; Estabilidad de las fluctuaciones locales a lo largo del tiempo.

Combinación de información entre sitios

En hidrología, se analizan series de datos de varios sitios compuestas por valores anuales del caudal máximo anual del río dentro del año. Un modelo común es que las distribuciones de estos valores son las mismas para todos los sitios, excepto un simple factor de escala, de modo que la ubicación y la escala están vinculadas de una manera simple. Entonces pueden surgir dudas sobre el examen de la homogeneidad entre sitios de la distribución de los valores escalados.

Combinación de fuentes de información

En meteorología, los conjuntos de datos meteorológicos se adquieren a lo largo de muchos años de registro y, como parte de esto, las mediciones en ciertas estaciones pueden cesar ocasionalmente mientras, aproximadamente al mismo tiempo, las mediciones pueden comenzar en ubicaciones cercanas. Entonces surgen dudas sobre si, si los registros se combinan para formar un único conjunto más largo de registros, esos registros pueden considerarse homogéneos a lo largo del tiempo. Un ejemplo de prueba de homogeneidad de datos de velocidad y dirección del viento se puede encontrar en Romanić et al., 2015.

Homogeneidad dentro de las poblaciones

Las encuestas de población simples pueden partir de la idea de que las respuestas serán homogéneas en toda la población. Evaluar la homogeneidad de la población implicaría observar si las respuestas de ciertas subpoblaciones identificables difieren de las de otras. Por ejemplo, los propietarios de automóviles pueden diferir de los no propietarios, o puede haber diferencias entre diferentes grupos de edad.

Pruebas

Una prueba de homogeneidad, en el sentido de equivalencia exacta de distribuciones estadísticas, puede basarse en una estadística E. Una prueba de ubicación prueba la hipótesis más simple de que las distribuciones tienen el mismo parámetro de ubicación.