Historia de las matemáticas

La historia de las matemáticas trata sobre el origen de los descubrimientos en matemáticas y los métodos matemáticos y la notación del pasado. Antes de la edad moderna y la difusión mundial del conocimiento, los ejemplos escritos de nuevos desarrollos matemáticos han salido a la luz solo en unos pocos lugares. A partir del 3000 a. C., los estados mesopotámicos de Sumer, Akkad y Asiria, seguidos de cerca por el Antiguo Egipto y el estado levantino de Ebla, comenzaron a utilizar la aritmética, el álgebra y la geometría con fines impositivos, comerciales, comerciales y también en los patrones de la naturaleza, el campo de la astronomía y registrar el tiempo y formular calendarios.

Los primeros textos matemáticos disponibles son de Mesopotamia y Egipto: Plimpton 322 (babilónico c. 2000 - 1900 a. C.), el papiro matemático Rhind (egipcio c. 1800 a. C.) y el papiro matemático de Moscú (egipcio c. 1890 a. C.). Todos estos textos mencionan las llamadas ternas pitagóricas, por lo que, por inferencia, el teorema de Pitágoras parece ser el desarrollo matemático más antiguo y extendido después de la aritmética básica y la geometría.

El estudio de las matemáticas como una "disciplina demostrativa" comenzó en el siglo VI a. C. con los pitagóricos, quienes acuñaron el término "matemáticas" del griego antiguo μάθημα (mathema), que significa "sujeto de instrucción". Las matemáticas griegas refinaron en gran medida los métodos (especialmente a través de la introducción del razonamiento deductivo y el rigor matemático en las pruebas) y ampliaron el tema de las matemáticas.Aunque prácticamente no hicieron contribuciones a las matemáticas teóricas, los antiguos romanos utilizaron las matemáticas aplicadas en topografía, ingeniería estructural, ingeniería mecánica, contabilidad, creación de calendarios lunares y solares e incluso artes y oficios. Las matemáticas chinas hicieron contribuciones tempranas, incluido un sistema de valor posicional y el primer uso de números negativos. El sistema numérico hindú-árabe y las reglas para el uso de sus operaciones, en uso en todo el mundo hoy en día, evolucionaron a lo largo del primer milenio d. C. en la India y se transmitieron al mundo occidental a través de las matemáticas islámicas a través del trabajo de Muḥammad ibn Mūsā. al-Khwārizmī. Las matemáticas islámicas, a su vez, desarrollaron y ampliaron las matemáticas conocidas por estas civilizaciones.Contemporáneas pero independientes de estas tradiciones fueron las matemáticas desarrolladas por la civilización maya de México y América Central, donde el concepto de cero recibió un símbolo estándar en los números mayas.

Muchos textos griegos y árabes sobre matemáticas se tradujeron al latín a partir del siglo XII, lo que condujo a un mayor desarrollo de las matemáticas en la Europa medieval. Desde la antigüedad hasta la Edad Media, los períodos de descubrimiento matemático a menudo fueron seguidos por siglos de estancamiento. Comenzando en la Italia del Renacimiento en el siglo XV, se realizaron nuevos desarrollos matemáticos, interactuando con nuevos descubrimientos científicos, a un ritmo creciente que continúa hasta el día de hoy. Esto incluye el trabajo innovador de Isaac Newton y Gottfried Wilhelm Leibniz en el desarrollo del cálculo infinitesimal durante el transcurso del siglo XVII. A fines del siglo XIX se fundó el Congreso Internacional de Matemáticos y continúa liderando los avances en el campo.

Europeo (descendiente del árabe occidental)	0	1	2	3	4	5	6	7	8	9
árabe-índico	٠	١	٢	٣	٤	٥	٦	٧	٨	٩
Árabe-índico oriental (persa y urdu)	۰	۱	۲	۳	۴	۵	۶	۷	۸	۹
Devanagari (Hindi)	०	१	२	३	४	५	६	७	८	९
Chino	〇	一	二	三	四	五	六	七	八	九
tamil		௧	௨	௩	௪	௫	௬	௭	௮	௯

Prehistórico

Los orígenes del pensamiento matemático se encuentran en los conceptos de número, patrones en la naturaleza, magnitud y forma. Los estudios modernos de la cognición animal han demostrado que estos conceptos no son exclusivos de los humanos. Tales conceptos habrían sido parte de la vida cotidiana en las sociedades de cazadores-recolectores. La idea de que el concepto de "número" evoluciona gradualmente con el tiempo está respaldada por la existencia de lenguajes que conservan la distinción entre "uno", "dos" y "muchos", pero no de números mayores de dos.

El hueso de Ishango, encontrado cerca de la cabecera del río Nilo (noreste del Congo), puede tener más de 20.000 años y consiste en una serie de marcas talladas en tres columnas a lo largo del hueso. Las interpretaciones comunes son que el hueso de Ishango muestra un recuento de la demostración más antigua conocida de secuencias de números primos o un calendario lunar de seis meses. Peter Rudman argumenta que el desarrollo del concepto de números primos solo podría haber ocurrido después del concepto de división, que data después del 10.000 a. C., y que los números primos probablemente no se entendieron hasta alrededor del 500 a. También escribe que "no se ha intentado explicar por qué una cuenta de algo debería mostrar múltiplos de dos, números primos entre 10 y 20, y algunos números que son casi múltiplos de 10".El hueso de Ishango, según el erudito Alexander Marshack, puede haber influido en el desarrollo posterior de las matemáticas en Egipto ya que, como algunas entradas en el hueso de Ishango, la aritmética egipcia también hizo uso de la multiplicación por 2; esto, sin embargo, está en disputa.

Los egipcios predinásticos del quinto milenio antes de Cristo representaban pictóricamente diseños geométricos. Se ha afirmado que los monumentos megalíticos de Inglaterra y Escocia, que datan del tercer milenio antes de Cristo, incorporan ideas geométricas como círculos, elipses y ternas pitagóricas en su diseño. Sin embargo, todo lo anterior está en disputa, y los documentos matemáticos indiscutibles más antiguos actualmente provienen de fuentes egipcias babilónicas y dinásticas.

Babilónico

Las matemáticas babilónicas se refieren a cualquier matemática de los pueblos de Mesopotamia (Irak moderno) desde los días de los primeros sumerios hasta el período helenístico casi hasta los albores del cristianismo. La mayoría del trabajo matemático babilónico proviene de dos períodos muy separados: los primeros cientos de años del segundo milenio a. C. (período babilónico antiguo) y los últimos siglos del primer milenio a. C. (período seléucida). Recibe el nombre de matemáticas babilónicas debido al papel central de Babilonia como lugar de estudio. Más tarde, bajo el Imperio Árabe, Mesopotamia, especialmente Bagdad, se convirtió una vez más en un importante centro de estudio de las matemáticas islámicas.

En contraste con la escasez de fuentes en las matemáticas egipcias, el conocimiento de las matemáticas babilónicas se deriva de más de 400 tablillas de arcilla desenterradas desde la década de 1850. Escritas en escritura cuneiforme, las tablillas se inscribían mientras la arcilla estaba húmeda y se horneaban en un horno o al calor del sol. Algunos de estos parecen ser tareas calificadas.

La evidencia más antigua de las matemáticas escritas se remonta a los antiguos sumerios, quienes construyeron la primera civilización en Mesopotamia. Desarrollaron un complejo sistema de metrología a partir del 3000 a. Desde alrededor del 2500 a. C. en adelante, los sumerios escribieron tablas de multiplicar en tablillas de arcilla y se ocuparon de ejercicios geométricos y problemas de división. Los primeros rastros de los números babilónicos también se remontan a este período.

Las matemáticas babilónicas se escribieron utilizando un sistema numérico sexagesimal (base 60). De esto se deriva el uso moderno de 60 segundos en un minuto, 60 minutos en una hora y 360 (60 × 6) grados en un círculo, así como el uso de segundos y minutos de arco para indicar fracciones de un grado.. Es probable que se escogiera el sistema sexagesimal porque 60 se puede dividir uniformemente entre 2, 3, 4, 5, 6, 10, 12, 15, 20 y 30. Además, a diferencia de los egipcios, griegos y romanos, los babilonios tenían un sistema de valor posicional, donde los dígitos escritos en la columna de la izquierda representaban valores más grandes, como en el sistema decimal.El poder del sistema de notación babilónico residía en que podía usarse para representar fracciones con tanta facilidad como números enteros; por lo tanto, multiplicar dos números que contenían fracciones no era diferente de multiplicar números enteros, similar a la notación moderna. El sistema de notación de los babilonios fue el mejor de cualquier civilización hasta el Renacimiento, y su poder le permitió lograr una notable precisión computacional; por ejemplo, la tablilla babilónica YBC 7289 da una aproximación de √ 2 con una precisión de cinco decimales. Sin embargo, los babilonios carecían de un equivalente del punto decimal, por lo que el valor posicional de un símbolo a menudo tenía que inferirse del contexto.Para el período seléucida, los babilonios habían desarrollado un símbolo cero como marcador de posición para las posiciones vacías; sin embargo, solo se usó para posiciones intermedias. Este signo cero no aparece en posiciones terminales, por lo que los babilonios se acercaron pero no desarrollaron un verdadero sistema de valor posicional.

Otros temas cubiertos por las matemáticas babilónicas incluyen fracciones, álgebra, ecuaciones cuadráticas y cúbicas, y el cálculo de números regulares y sus pares recíprocos. Las tabletas también incluyen tablas de multiplicar y métodos para resolver ecuaciones lineales, cuadráticas y cúbicas, un logro notable para la época. Las tablillas del período babilónico antiguo también contienen la declaración más antigua conocida del teorema de Pitágoras. Sin embargo, al igual que con las matemáticas egipcias, las matemáticas babilónicas no muestran conciencia de la diferencia entre soluciones exactas y aproximadas, o la capacidad de resolución de un problema y, lo que es más importante, ninguna declaración explícita de la necesidad de pruebas o principios lógicos.

Egipcio

Las matemáticas egipcias se refieren a las matemáticas escritas en el idioma egipcio. Desde el período helenístico, el griego reemplazó al egipcio como lengua escrita de los eruditos egipcios. El estudio matemático en Egipto continuó más tarde bajo el Imperio Árabe como parte de las matemáticas islámicas, cuando el árabe se convirtió en el idioma escrito de los eruditos egipcios. La evidencia arqueológica ha sugerido que el sistema de conteo del Antiguo Egipto tuvo su origen en el África subsahariana. Además, los diseños de geometría fractal que están muy extendidos entre las culturas del África subsahariana también se encuentran en la arquitectura egipcia y en los signos cosmológicos.

El texto matemático egipcio más extenso es el papiro de Rhind (a veces también llamado Papiro de Ahmes por su autor), que data de c. 1650 a. C., pero probablemente una copia de un documento más antiguo del Reino Medio de aproximadamente 2000-1800 a. C. Es un manual de instrucciones para estudiantes de aritmética y geometría. Además de dar fórmulas de área y métodos para multiplicar, dividir y trabajar con fracciones unitarias, también contiene evidencia de otros conocimientos matemáticos, incluidos números compuestos y primos; medios aritméticos, geométricos y armónicos; y comprensiones simplistas tanto de la criba de Eratóstenes como de la teoría de los números perfectos (a saber, la del número 6). También muestra cómo resolver ecuaciones lineales de primer orden, así como series aritméticas y geométricas.

Otro texto matemático egipcio significativo es el papiro de Moscú, también del período del Reino Medio, fechado en c. 1890 a.C. Consiste en lo que hoy en día se denomina problemas verbales o problemas narrativos, que aparentemente tenían como finalidad el entretenimiento. Se considera que un problema es de particular importancia porque proporciona un método para encontrar el volumen de un tronco (pirámide truncada).

Finalmente, el Papiro de Berlín 6619 (c. 1800 a. C.) muestra que los antiguos egipcios podían resolver una ecuación algebraica de segundo orden.

Griego

Las matemáticas griegas se refieren a las matemáticas escritas en griego desde la época de Tales de Mileto (~600 a. C.) hasta el cierre de la Academia de Atenas en el 529 d. C. Los matemáticos griegos vivían en ciudades repartidas por todo el Mediterráneo oriental, desde Italia hasta el norte de África, pero estaban unidos por la cultura y el idioma. Las matemáticas griegas del período posterior a Alejandro Magno a veces se denominan matemáticas helenísticas.

Las matemáticas griegas eran mucho más sofisticadas que las matemáticas desarrolladas por culturas anteriores. Todos los registros supervivientes de las matemáticas anteriores a la Grecia muestran el uso del razonamiento inductivo, es decir, observaciones repetidas utilizadas para establecer reglas generales. Los matemáticos griegos, por el contrario, utilizaron el razonamiento deductivo. Los griegos usaban la lógica para sacar conclusiones de definiciones y axiomas, y usaban el rigor matemático para demostrarlos.

Se cree que las matemáticas griegas comenzaron con Tales de Mileto (c. 624–c. 546 a. C.) y Pitágoras de Samos (c. 582–c. 507 a. C.). Aunque se discute el alcance de la influencia, probablemente se inspiraron en las matemáticas egipcias y babilónicas. Según la leyenda, Pitágoras viajó a Egipto para aprender matemáticas, geometría y astronomía de los sacerdotes egipcios.

Thales usó la geometría para resolver problemas como calcular la altura de las pirámides y la distancia de los barcos a la costa. Se le atribuye el primer uso del razonamiento deductivo aplicado a la geometría, al derivar cuatro corolarios del teorema de Tales. Como resultado, ha sido aclamado como el primer verdadero matemático y la primera persona conocida a quien se le ha atribuido un descubrimiento matemático. Pitágoras estableció la Escuela Pitágoras, cuya doctrina era que las matemáticas gobernaban el universo y cuyo lema era "Todo es número". Fueron los pitagóricos quienes acuñaron el término "matemáticas", y con quienes comienza el estudio de las matemáticas por sí mismas. A los pitagóricos se les atribuye la primera prueba del teorema de Pitágoras,aunque el enunciado del teorema tiene una larga historia, y con la demostración de la existencia de los números irracionales. Aunque fue precedido por los babilonios y los chinos, el matemático neopitagórico Nicómaco (60-120 d. C.) proporcionó una de las primeras tablas de multiplicar grecorromanas, mientras que la tabla de multiplicar griega más antigua que existe se encuentra en una tablilla de cera que data del siglo I. AD (ahora se encuentra en el Museo Británico). La asociación de los neopitagóricos con la invención occidental de la tabla de multiplicar es evidente en su nombre medieval posterior: mensa Pythagorica.

Platón (428/427 a. C. – 348/347 a. C.) es importante en la historia de las matemáticas por inspirar y guiar a otros. Su Academia Platónica, en Atenas, se convirtió en el centro matemático del mundo en el siglo IV a. C., y fue de esta escuela de donde provinieron los principales matemáticos de la época, como Eudoxo de Cnido. Platón también discutió los fundamentos de las matemáticas, aclaró algunas de las definiciones (por ejemplo, la de una línea como "longitud sin anchura") y reorganizó las suposiciones. El método analítico se atribuye a Platón, mientras que una fórmula para obtener ternas pitagóricas lleva su nombre.

Eudoxo (408–c. 355 a. C.) desarrolló el método de agotamiento, un precursor de la integración moderna y una teoría de las proporciones que evitó el problema de las magnitudes inconmensurables. El primero permitió los cálculos de áreas y volúmenes de figuras curvilíneas, mientras que el segundo permitió a los geómetras posteriores realizar avances significativos en geometría. Aunque no hizo descubrimientos matemáticos técnicos específicos, Aristóteles (384–c. 322 a. C.) contribuyó significativamente al desarrollo de las matemáticas al sentar las bases de la lógica.

En el siglo III a. C., el principal centro de educación e investigación matemática era el Museo de Alejandría. Fue allí donde Euclides (c. 300 a. C.) enseñó y escribió los Elementos, ampliamente considerado el libro de texto más exitoso e influyente de todos los tiempos. Los Elementos introdujeron el rigor matemático a través del método axiomático y es el primer ejemplo del formato que todavía se usa en las matemáticas hoy en día, el de definición, axioma, teorema y prueba. Aunque la mayor parte del contenido de los Elementos ya se conocía, Euclides los arregló en un marco lógico único y coherente. los elementosfue conocido por todas las personas educadas en Occidente hasta mediados del siglo XX y sus contenidos todavía se enseñan en las clases de geometría en la actualidad. Además de los teoremas familiares de la geometría euclidiana, los Elementos se concibieron como un libro de texto introductorio a todos los temas matemáticos de la época, como la teoría de números, el álgebra y la geometría sólida, incluidas las pruebas de que la raíz cuadrada de dos es irracional y que hay infinitos números primos. Euclides también escribió extensamente sobre otros temas, como secciones cónicas, óptica, geometría esférica y mecánica, pero solo sobrevive la mitad de sus escritos.

Arquímedes (c. 287-212 a. C.) de Siracusa, considerado el mayor matemático de la antigüedad, utilizó el método de agotamiento para calcular el área bajo el arco de una parábola con la suma de una serie infinita, de una manera no muy diferente de cálculo moderno. También demostró que se podía usar el método de agotamiento para calcular el valor de π con tanta precisión como se deseara, y obtuvo el valor de π más exacto conocido en ese momento, 310/71< π < 310/70. También estudió la espiral que lleva su nombre, obtuvo fórmulas para los volúmenes de las superficies de revolución (paraboloide, elipsoide, hiperboloide) y un ingenioso método de exponenciación para expresar números muy grandes. Si bien también es conocido por sus contribuciones a la física y varios dispositivos mecánicos avanzados, el propio Arquímedes valoró mucho más los productos de su pensamiento y los principios matemáticos generales. Consideró como su mayor logro su hallazgo del área de superficie y el volumen de una esfera, que obtuvo al demostrar que estos son 2/3 del área de superficie y el volumen de un cilindro que circunscribe la esfera.

Apolonio de Perga (c. 262-190 a. C.) hizo avances significativos en el estudio de las secciones cónicas, demostrando que se pueden obtener las tres variedades de secciones cónicas variando el ángulo del plano que corta un cono de doble siesta. También acuñó la terminología que se usa hoy en día para las secciones cónicas, a saber, parábola ("lugar al lado" o "comparación"), "elipse" ("deficiencia") e "hipérbola" ("un tiro más allá"). Su trabajo Conics es uno de los trabajos matemáticos más conocidos y conservados de la antigüedad, y en él deriva muchos teoremas sobre las secciones cónicas que resultarían invaluables para los matemáticos y astrónomos posteriores que estudiaron el movimiento planetario, como Isaac Newton.Si bien ni Apolonio ni ningún otro matemático griego dieron el salto a la geometría de coordenadas, el tratamiento de las curvas por parte de Apolonio es en cierto modo similar al tratamiento moderno, y parte de su trabajo parece anticipar el desarrollo de la geometría analítica por parte de Descartes unos 1800 años después.

Casi al mismo tiempo, Eratóstenes de Cirene (c. 276–194 a. C.) ideó la criba de Eratóstenes para encontrar números primos. El siglo III a. C. se considera generalmente como la "Edad de oro" de las matemáticas griegas, con avances en matemáticas puras a partir de ahora en relativo declive. Sin embargo, en los siglos que siguieron se hicieron avances significativos en las matemáticas aplicadas, sobre todo en la trigonometría, en gran parte para abordar las necesidades de los astrónomos. Hiparco de Nicea (c. 190-120 a. C.) es considerado el fundador de la trigonometría por compilar la primera tabla trigonométrica conocida, ya él también se le debe el uso sistemático del círculo de 360 ​​grados.A Heron de Alejandría (c. 10-70 d. C.) se le atribuye la fórmula de Heron para encontrar el área de un triángulo escaleno y ser el primero en reconocer la posibilidad de que los números negativos posean raíces cuadradas. Menelao de Alejandría (c. 100 dC) fue pionero en la trigonometría esférica a través del teorema de Menelao. El trabajo trigonométrico más completo e influyente de la antigüedad es el Almagesto de Ptolomeo (c. 90-168 d. C.), un tratado astronómico histórico cuyas tablas trigonométricas serían utilizadas por los astrónomos durante los siguientes mil años. A Ptolomeo también se le atribuye el teorema de Ptolomeo para derivar cantidades trigonométricas y el valor más preciso de π fuera de China hasta el período medieval, 3.1416.

Después de un período de estancamiento después de Ptolomeo, el período entre el 250 y el 350 d. C. a veces se denomina la "Edad de Plata" de las matemáticas griegas. Durante este período, Diofanto hizo avances significativos en álgebra, particularmente en el análisis indeterminado, que también se conoce como "análisis diofántico". El estudio de las ecuaciones diofánticas y las aproximaciones diofánticas es un área importante de investigación hasta el día de hoy. Su obra principal fue la Aritmética, una colección de 150 problemas algebraicos que tratan con soluciones exactas a ecuaciones determinadas e indeterminadas. La Aritmética tuvo una influencia significativa en matemáticos posteriores, como Pierre de Fermat, quien llegó a su famoso Último Teorema después de intentar generalizar un problema que había leído en elAritmética (la de dividir un cuadrado en dos cuadrados). Diofanto también hizo avances significativos en la notación, siendo la Arithmetica la primera instancia de simbolismo algebraico y síncopa.

Entre los últimos grandes matemáticos griegos se encuentra Pappus de Alejandría (siglo IV d. C.). Es conocido por su teorema del hexágono y el teorema del centroide, así como por la configuración de Pappus y el gráfico de Pappus. Su colección es una fuente importante de conocimiento sobre las matemáticas griegas, ya que la mayor parte ha sobrevivido. Pappus es considerado el último gran innovador en las matemáticas griegas, y el trabajo posterior consiste principalmente en comentarios sobre trabajos anteriores.

La primera mujer matemática registrada por la historia fue Hipatia de Alejandría (350-415 d. C.). Sucedió a su padre (Teón de Alejandría) como bibliotecaria en la Gran Biblioteca y escribió muchas obras sobre matemáticas aplicadas. Debido a una disputa política, la comunidad cristiana de Alejandría la hizo desnudar públicamente y ejecutarla. Su muerte a veces se toma como el final de la era de las matemáticas griegas alejandrinas, aunque el trabajo continuó en Atenas durante otro siglo con figuras como Proclo, Simplicius y Eutocius. Aunque Proclo y Simplicius eran más filósofos que matemáticos, sus comentarios sobre obras anteriores son fuentes valiosas sobre las matemáticas griegas. El cierre de la Academia neoplatónica de Atenas por parte del emperador Justiniano en 529 d. C. se considera tradicionalmente como el final de la era de las matemáticas griegas, aunque la tradición griega continuó intacta en el imperio bizantino con matemáticos como Antemio de Tralles e Isidoro. de Mileto, los arquitectos de Hagia Sophia. Sin embargo, las matemáticas bizantinas consistían principalmente en comentarios, con poca innovación, y los centros de innovación matemática se encontraban en otros lugares en ese momento.

Romano

Aunque los matemáticos de etnia griega continuaron bajo el dominio de la República romana tardía y el posterior Imperio romano, no hubo matemáticos latinos nativos dignos de mención en comparación. Los antiguos romanos, como Cicerón (106-43 a. C.), un influyente estadista romano que estudió matemáticas en Grecia, creían que los agrimensores y los calculadores romanos estaban mucho más interesados ​​en las matemáticas aplicadas que en las matemáticas teóricas y la geometría que tanto valoraban los griegos. No está claro si los romanos primero derivaron su sistema numérico directamente del precedente griego o de los números etruscos utilizados por la civilización etrusca centrada en lo que ahora es Toscana, Italia central.

Usando el cálculo, los romanos eran expertos tanto en instigar como en detectar fraudes financieros, así como en administrar impuestos para el tesoro. Siculus Flaccus, uno de los gromatici romanos (es decir, agrimensor), escribió las Categorías de campos, que ayudaron a los agrimensores romanos a medir las superficies de las tierras y territorios asignados. Además de administrar el comercio y los impuestos, los romanos también aplicaron regularmente las matemáticas para resolver problemas de ingeniería, incluida la construcción de arquitectura como puentes, construcción de carreteras y preparación para campañas militares.Artes y oficios como los mosaicos romanos, inspirados en diseños griegos anteriores, crearon patrones geométricos ilusionistas y escenas ricas y detalladas que requerían medidas precisas para cada tesela, las piezas de opus tessellatum en promedio medían ocho milímetros cuadrados y las piezas más finas de opus vermiculatum tenían una superficie media de cuatro milímetros cuadrados.

La creación del calendario romano también requirió matemáticas básicas. El primer calendario supuestamente data del siglo VIII a. C. durante el Reino Romano e incluía 356 días más un año bisiesto cada dos años. En contraste, el calendario lunar de la era republicana contenía 355 días, aproximadamente diez y un cuarto días menos que el año solar, una discrepancia que se resolvió agregando un mes adicional al calendario después del 23 de febrero. Este calendario fue reemplazado por el calendario juliano, un calendario solar organizado por Julio César (100–44 a. C.) e ideado por Sosígenes de Alejandría para incluir un día bisiesto cada cuatro años en un ciclo de 365 días. Este calendario, que contenía un error de 11 minutos y 14 segundos, fue posteriormente corregido por el calendario gregoriano organizado por el Papa Gregorio XIII (R. 1572-1585), prácticamente el mismo calendario solar que se usa en los tiempos modernos como calendario estándar internacional.

Aproximadamente al mismo tiempo, los chinos Han y los romanos inventaron el odómetro con ruedas para medir las distancias recorridas, el modelo romano descrito por primera vez por el ingeniero civil y arquitecto romano Vitruvio (c. 80 a. C. - c. 15 a. C.). El dispositivo se usó al menos hasta el reinado del emperador Cómodo (r. 177 - 192 d. C.), pero su diseño parece haberse perdido hasta que se realizaron experimentos durante el siglo XV en Europa occidental.Quizás basándose en un engranaje y una tecnología similares que se encuentran en el mecanismo de Antikythera, el odómetro de Vitruvio presentaba ruedas de carro que medían 4 pies (1,2 m) de diámetro girando cuatrocientas veces en una milla romana (aproximadamente 4590 pies/1400 m). Con cada revolución, un dispositivo de pasador y eje engranaba una rueda dentada de 400 dientes que hacía girar una segunda marcha responsable de dejar caer guijarros en una caja, cada guijarro representaba una milla recorrida.

Chino

Un análisis de las primeras matemáticas chinas ha demostrado su desarrollo único en comparación con otras partes del mundo, lo que lleva a los académicos a suponer un desarrollo completamente independiente. El texto matemático más antiguo existente de China es el Zhoubi Suanjing, fechado de diversas formas entre 1200 a. C. y 100 a. C., aunque parece razonable una fecha de alrededor de 300 a. C. durante el Período de los Reinos Combatientes. Sin embargo, Tsinghua Bamboo Slips, que contiene la tabla de multiplicación decimal más antigua conocida (aunque los antiguos babilonios tenían una con una base de 60), está fechada alrededor del 305 a. C. y es quizás el texto matemático más antiguo que se conserva de China.

De particular interés es el uso en las matemáticas chinas de un sistema de notación posicional decimal, los llamados "números de barra" en los que se usaron distintos cifrados para números entre 1 y 10, y cifrados adicionales para potencias de diez. Por lo tanto, el número 123 se escribiría usando el símbolo de "1", seguido del símbolo de "100", luego el símbolo de "2" seguido del símbolo de "10", seguido del símbolo de "3". Este era el sistema numérico más avanzado del mundo en ese momento, aparentemente en uso varios siglos antes de la era común y mucho antes del desarrollo del sistema numérico indio. Los números de varilla permitieron la representación de números tan grandes como se deseara y permitieron realizar cálculos en el suan pan. o ábaco chino. La fecha de la invención delsuan pan no es seguro, pero la primera mención escrita data del año 190 d. C., en las Notas complementarias sobre el arte de las figuras de Xu Yue.

El trabajo más antiguo existente sobre geometría en China proviene del canon filosófico mohista c. 330 a. C., compilado por los seguidores de Mozi (470–390 a. C.). El Mo Jing describió varios aspectos de muchos campos asociados con la ciencia física y también proporcionó una pequeña cantidad de teoremas geométricos. También definió los conceptos de circunferencia, diámetro, radio y volumen.

En 212 a. C., el emperador Qin Shi Huang ordenó que se quemaran todos los libros del Imperio Qin que no fueran los aprobados oficialmente. Este decreto no fue obedecido universalmente, pero como consecuencia de esta orden poco se sabe acerca de las antiguas matemáticas chinas antes de esta fecha. Después de la quema de libros del 212 a. C., la dinastía Han (202 a. C.-220 d. C.) produjo obras de matemáticas que presumiblemente ampliaron las obras que ahora están perdidas. El más importante de ellos es Los nueve capítulos sobre el arte matemático, cuyo título completo apareció en el año 179 d. C., pero existía en parte con otros títulos anteriormente. Consta de 246 problemas verbales relacionados con la agricultura, los negocios, el empleo de la geometría para calcular los tramos de altura y las relaciones de dimensión de las torres de las pagodas chinas, la ingeniería, la agrimensura e incluye material sobre triángulos rectángulos.Creó una prueba matemática para el teorema de Pitágoras y una fórmula matemática para la eliminación gaussiana. El tratado también proporciona valores de π, que los matemáticos chinos originalmente aproximaron como 3 hasta que Liu Xin (m. 23 d. C.) proporcionó una cifra de 3,1457 y, posteriormente, Zhang Heng (78–139) aproximó pi como 3,1724, así como 3,162 tomando la raíz cuadrada de 10. Liu Hui comentó sobre los Nueve Capítulos en el siglo III dC y dio un valor de π con una precisión de 5 decimales (es decir, 3,14159).Aunque más una cuestión de resistencia computacional que de conocimiento teórico, en el siglo V d. C., Zu Chongzhi calculó el valor de π con siete decimales (es decir, 3,141592), que siguió siendo el valor más preciso de π durante casi los siguientes 1000 años. También estableció un método que más tarde se llamaría principio de Cavalieri para encontrar el volumen de una esfera.

El punto culminante de las matemáticas chinas se produjo en el siglo XIII durante la segunda mitad de la dinastía Song (960-1279), con el desarrollo del álgebra china. El texto más importante de ese período es el Espejo precioso de los cuatro elementos de Zhu Shijie (1249-1314), que trata sobre la solución de ecuaciones algebraicas simultáneas de orden superior utilizando un método similar al método de Horner. The Precious Mirror también contiene un diagrama del triángulo de Pascal con coeficientes de expansiones binomiales hasta la octava potencia, aunque ambos aparecen en obras chinas desde 1100. Los chinos también hicieron uso del complejo diagrama combinatorio conocido como el cuadrado mágico y los círculos mágicos. descrito en la antigüedad y perfeccionado por Yang Hui (1238-1298 d. C.).

Incluso después de que las matemáticas europeas comenzaran a florecer durante el Renacimiento, las matemáticas europeas y chinas eran tradiciones separadas, con una importante producción matemática china en declive desde el siglo XIII en adelante. Misioneros jesuitas como Matteo Ricci llevaron ideas matemáticas de un lado a otro entre las dos culturas desde el siglo XVI hasta el siglo XVIII, aunque en ese momento entraban en China muchas más ideas matemáticas de las que salían.

Las matemáticas japonesas, las matemáticas coreanas y las matemáticas vietnamitas se consideran tradicionalmente como derivadas de las matemáticas chinas y pertenecientes a la esfera cultural de Asia oriental basada en el confucianismo. Las matemáticas coreanas y japonesas estuvieron fuertemente influenciadas por las obras algebraicas producidas durante la dinastía Song de China, mientras que las matemáticas vietnamitas estaban muy endeudadas con las obras populares de la dinastía Ming de China (1368-1644). Por ejemplo, aunque los tratados matemáticos vietnamitas se escribieron en chino o en la escritura nativa vietnamita Chữ Nôm, todos ellos siguieron el formato chino de presentar una colección de problemas con algoritmos para resolverlos, seguidos de respuestas numéricas.Las matemáticas en Vietnam y Corea se asociaron principalmente con la burocracia de la corte profesional de matemáticos y astrónomos, mientras que en Japón prevaleció más en el ámbito de las escuelas privadas.

Indio

La civilización más antigua del subcontinente indio es la civilización del valle del Indo (fase madura: 2600 a 1900 a. C.) que floreció en la cuenca del río Indo. Sus ciudades fueron diseñadas con regularidad geométrica, pero no sobreviven documentos matemáticos conocidos de esta civilización.

Los registros matemáticos más antiguos de la India son los Sulba Sutras (fechados entre el siglo VIII a. C. y el siglo II d. C.), apéndices de textos religiosos que brindan reglas simples para construir altares de varias formas, como cuadrados, rectángulos, paralelogramos y otros. Al igual que con Egipto, la preocupación por las funciones del templo apunta a un origen de las matemáticas en el ritual religioso. Los Sulba Sutras dan métodos para construir un círculo con aproximadamente la misma área que un cuadrado dado, lo que implica varias aproximaciones diferentes del valor de π. Además, calculan la raíz cuadrada de 2 con varios lugares decimales, enumeran las ternas de Pitágoras y dan una declaración del teorema de Pitágoras.Todos estos resultados están presentes en las matemáticas babilónicas, lo que indica la influencia mesopotámica. No se sabe en qué medida los Sulba Sutras influyeron en los matemáticos indios posteriores. Como en China, hay una falta de continuidad en las matemáticas indias; los avances significativos están separados por largos períodos de inactividad.

Pāṇini (c. Siglo V a. C.) formuló las reglas para la gramática sánscrita. Su notación era similar a la notación matemática moderna y usaba metarreglas, transformaciones y recursividad. Pingala (aproximadamente entre los siglos III y I a. C.) en su tratado de prosodia utiliza un dispositivo correspondiente a un sistema numérico binario. Su discusión sobre la combinatoria de metros corresponde a una versión elemental del teorema del binomio. El trabajo de Pingala también contiene las ideas básicas de los números de Fibonacci (llamados mātrāmeru).

Los siguientes documentos matemáticos significativos de la India después de los Sulba Sutras son los Siddhantas, tratados astronómicos de los siglos IV y V d. C. (período Gupta) que muestran una fuerte influencia helenística. Son significativos porque contienen la primera instancia de relaciones trigonométricas basadas en la media cuerda, como es el caso de la trigonometría moderna, en lugar de la cuerda completa, como era el caso de la trigonometría ptolemaica. A través de una serie de errores de traducción, las palabras "seno" y "coseno" derivan del sánscrito "jiya" y "kojiya".

Alrededor del año 500 d. C., Aryabhata escribió Aryabhatiya, un volumen delgado, escrito en verso, destinado a complementar las reglas de cálculo utilizadas en astronomía y medición matemática, aunque sin sensibilidad por la lógica o la metodología deductiva. Aunque aproximadamente la mitad de las entradas son incorrectas, es en Aryabhatiya donde aparece por primera vez el sistema de valor posicional decimal. Varios siglos después, el matemático musulmán Abu Rayhan Biruni describió el Aryabhatiya como una "mezcla de guijarros comunes y cristales costosos".

En el siglo VII, Brahmagupta identificó el teorema de Brahmagupta, la identidad de Brahmagupta y la fórmula de Brahmagupta, y por primera vez, en Brahma-sphuta-siddhanta, explicó lúcidamente el uso del cero como marcador de posición y dígito decimal, y explicó el hinduismo: Sistema de numeración arábiga.Fue a partir de una traducción de este texto indio sobre matemáticas (c. 770) que los matemáticos islámicos conocieron este sistema numérico, que adaptaron como números arábigos. Los eruditos islámicos llevaron el conocimiento de este sistema numérico a Europa en el siglo XII y ahora ha desplazado a todos los sistemas numéricos más antiguos en todo el mundo. Se utilizan varios conjuntos de símbolos para representar números en el sistema de numeración hindú-árabe, todos los cuales evolucionaron a partir de los números de Brahmi. Cada una de las aproximadamente doce escrituras principales de la India tiene sus propios glifos numéricos. En el siglo X, el comentario de Halayudha sobre el trabajo de Pingala contiene un estudio de la secuencia de Fibonacci y el triángulo de Pascal, y describe la formación de una matriz.

En el siglo XII, Bhāskara II vivió en el sur de la India y escribió extensamente sobre todas las ramas conocidas de las matemáticas. Su obra contiene objetos matemáticos equivalentes o aproximadamente equivalentes a infinitesimales, derivadas, el teorema del valor medio y la derivada de la función seno. Hasta qué punto anticipó la invención del cálculo es un tema controvertido entre los historiadores de las matemáticas.

En el siglo XIV, Madhava de Sangamagrama, el fundador de la Escuela de Matemáticas de Kerala, encontró la serie Madhava-Leibniz y obtuvo de ella una serie transformada, cuyos primeros 21 términos utilizó para calcular el valor de π como 3,14159265359. Madhava también encontró la serie de Madhava-Gregory para determinar el arcotangente, la serie de potencias de Madhava-Newton para determinar el seno y el coseno y la aproximación de Taylor para funciones de seno y coseno. En el siglo XVI, Jyesthadeva consolidó muchos de los desarrollos y teoremas de la Escuela de Kerala en el Yukti-bhāṣā. Se ha argumentado que los avances de la escuela de Kerala, que sentó las bases del cálculo, se transmitieron a Europa en el siglo XVI.a través de misioneros jesuitas y comerciantes que estaban activos alrededor del antiguo puerto de Muziris en ese momento y, como resultado, influyeron directamente en los desarrollos europeos posteriores en análisis y cálculo. Sin embargo, otros académicos argumentan que la Escuela de Kerala no formuló una teoría sistemática de diferenciación e integración, y que no hay evidencia directa de que sus resultados se transmitan fuera de Kerala.

Imperios islámicos

El Imperio Islámico establecido en Persia, Oriente Medio, Asia Central, África del Norte, Iberia y partes de la India en el siglo VIII hizo contribuciones significativas a las matemáticas. Aunque la mayoría de los textos islámicos sobre matemáticas fueron escritos en árabe, la mayoría de ellos no fueron escritos por árabes, ya que, al igual que el griego en el mundo helenístico, el árabe se usaba como lengua escrita de los eruditos no árabes en todo el mundo islámico. tiempo. Los persas contribuyeron al mundo de las Matemáticas junto a los árabes.

En el siglo IX, el matemático persa Muḥammad ibn Mūsā al-Khwārizmī escribió un importante libro sobre los números arábigos hindúes y uno sobre métodos para resolver ecuaciones. Su libro Sobre el cálculo con números hindúes, escrito alrededor de 825, junto con el trabajo de Al-Kindi, fueron fundamentales para difundir las matemáticas indias y los números indios en Occidente. La palabra algoritmo se deriva de la latinización de su nombre, Algoritmi, y la palabra álgebra del título de una de sus obras, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa'l-muqābala (El libro compendio sobre el cálculo por Terminación y Equilibrio). Dio una explicación exhaustiva de la solución algebraica de ecuaciones cuadráticas con raíces positivas,y fue el primero en enseñar álgebra en forma elemental y por sí misma. También discutió el método fundamental de "reducción" y "equilibrio", refiriéndose a la transposición de términos restados al otro lado de una ecuación, es decir, la cancelación de términos similares en lados opuestos de la ecuación. Esta es la operación que al-Khwārizmī describió originalmente como al-jabr.Su álgebra ya no se ocupaba "de una serie de problemas a resolver, sino de una exposición que parte de términos primitivos en los que las combinaciones deben dar todos los prototipos posibles de ecuaciones, que en adelante constituyen explícitamente el verdadero objeto de estudio". También estudió una ecuación por sí misma y "de manera genérica, en la medida en que no surge simplemente en el curso de la resolución de un problema, sino que está específicamente llamada a definir una clase infinita de problemas".

En Egipto, Abu Kamil extendió el álgebra al conjunto de números irracionales, aceptando raíces cuadradas y raíces cuartas como soluciones y coeficientes de ecuaciones cuadráticas. También desarrolló técnicas utilizadas para resolver tres ecuaciones simultáneas no lineales con tres variables desconocidas. Una característica única de sus obras fue tratar de encontrar todas las soluciones posibles a algunos de sus problemas, incluida una en la que encontró 2676 soluciones. Sus trabajos formaron una base importante para el desarrollo del álgebra e influyeron en matemáticos posteriores, como al-Karaji y Fibonacci.

Al-Karaji realizó más desarrollos en álgebra en su tratado al-Fakhri, donde amplía la metodología para incorporar potencias enteras y raíces enteras de cantidades desconocidas. Algo parecido a una prueba por inducción matemática aparece en un libro escrito por Al-Karaji alrededor del año 1000 dC, quien lo usó para probar el teorema del binomio, el triángulo de Pascal y la suma de cubos integrales. El historiador de las matemáticas, F. Woepcke,elogió a Al-Karaji por ser "el primero que introdujo la teoría del cálculo algebraico". También en el siglo X, Abul Wafa tradujo las obras de Diofanto al árabe. Ibn al-Haytham fue el primer matemático en derivar la fórmula para la suma de las cuartas potencias, utilizando un método fácilmente generalizable para determinar la fórmula general para la suma de las potencias integrales. Realizó una integración para encontrar el volumen de un paraboloide y pudo generalizar su resultado para las integrales de polinomios hasta el cuarto grado. Por lo tanto, estuvo cerca de encontrar una fórmula general para las integrales de polinomios, pero no se preocupó de ningún polinomio superior al cuarto grado.

A finales del siglo XI, Omar Khayyam escribió Discusiones sobre las dificultades de Euclides, un libro sobre lo que percibía como fallas en los Elementos de Euclides, especialmente el postulado paralelo. También fue el primero en encontrar la solución geométrica general de las ecuaciones cúbicas. También fue muy influyente en la reforma del calendario.

En el siglo XIII, Nasir al-Din Tusi (Nasireddin) hizo avances en trigonometría esférica. También escribió un trabajo influyente sobre el postulado paralelo de Euclides. En el siglo XV, Ghiyath al-Kashi calculó el valor de π al decimosexto lugar decimal. Kashi también tenía un algoritmo para calcular raíces enésimas, que era un caso especial de los métodos dados muchos siglos después por Ruffini y Horner.

Otros logros de los matemáticos musulmanes durante este período incluyen la adición de la notación del punto decimal a los números arábigos, el descubrimiento de todas las funciones trigonométricas modernas además del seno, la introducción del criptoanálisis y el análisis de frecuencia de al-Kindi, el desarrollo de la geometría analítica por parte de Ibn al-Haytham, el comienzo de la geometría algebraica por Omar Khayyam y el desarrollo de una notación algebraica por al-Qalasādī.

Durante la época del Imperio Otomano y el Imperio Safavid del siglo XV, el desarrollo de las matemáticas islámicas se estancó.

Maya

En las Américas precolombinas, la civilización maya que floreció en México y América Central durante el primer milenio d. C. desarrolló una tradición matemática única que, debido a su aislamiento geográfico, era completamente independiente de las matemáticas europeas, egipcias y asiáticas existentes. Los números mayas utilizaron una base de veinte, el sistema vigesimal, en lugar de una base de diez que forma la base del sistema decimal utilizado por la mayoría de las culturas modernas. Los mayas usaron las matemáticas para crear el calendario maya, así como para predecir fenómenos astronómicos en su astronomía maya nativa. Si bien el concepto de cero tuvo que inferirse en las matemáticas de muchas culturas contemporáneas, los mayas desarrollaron un símbolo estándar para él.

Europeo medieval

El interés de los europeos medievales por las matemáticas estaba impulsado por preocupaciones muy diferentes a las de los matemáticos modernos. Un elemento impulsor fue la creencia de que las matemáticas proporcionaban la clave para comprender el orden creado de la naturaleza, justificado con frecuencia por el Timeo de Platón y el pasaje bíblico (en el Libro de la Sabiduría) de que Dios había ordenado todas las cosas en medida, número y peso.

Boecio proporcionó un lugar para las matemáticas en el plan de estudios en el siglo VI cuando acuñó el término quadrivium para describir el estudio de la aritmética, la geometría, la astronomía y la música. Escribió De Institutione arithmetica, una traducción libre del griego de la Introducción a la aritmética de Nicómaco; De Institutione musica, también derivada de fuentes griegas; y una serie de extractos de los Elementos de Euclides. Sus obras eran más teóricas que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.

En el siglo XII, eruditos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluido The Compendious Book on Calculation by Completion and Balancing de al-Khwārizmī, traducido al latín por Robert of Chester, y el texto completo de Euclid's Elements, traducido en varios idiomas. versiones de Adelardo de Bath, Herman de Carintia y Gerardo de Cremona. Estas y otras nuevas fuentes provocaron una renovación de las matemáticas.

Leonardo de Pisa, ahora conocido como Fibonacci, aprendió por casualidad sobre los números arábigos hindúes en un viaje a lo que ahora es Béjaïa, Argelia, con su padre comerciante. (Europa todavía usaba números romanos). Allí, observó un sistema de aritmética (específicamente algorismo) que, debido a la notación posicional de los números arábigos hindúes, era mucho más eficiente y facilitaba enormemente el comercio. Leonardo escribió el Liber Abaci en 1202 (actualizado en 1254) introduciendo la técnica en Europa y comenzando un largo período de popularización. El libro también trajo a Europa lo que ahora se conoce como la secuencia de Fibonacci (conocida por los matemáticos indios durante cientos de años antes de eso) que se usó como un ejemplo anodino dentro del texto.

El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Una contribución importante fue el desarrollo de las matemáticas del movimiento local.

Thomas Bradwardine propuso que la velocidad (V) aumenta en proporción aritmética a medida que la relación entre la fuerza (F) y la resistencia (R) aumenta en proporción geométrica. Bradwardine expresó esto mediante una serie de ejemplos específicos, pero aunque el logaritmo aún no había sido concebido, podemos expresar su conclusión de forma anacrónica escribiendo: V = log (F/R). El análisis de Bradwardine es un ejemplo de la transferencia de una técnica matemática utilizada por al-Kindi y Arnald of Villanova para cuantificar la naturaleza de los medicamentos compuestos a un problema físico diferente.

Uno de los calculadores de Oxford del siglo XIV, William Heytesbury, que carecía de cálculo diferencial y del concepto de límites, propuso medir la velocidad instantánea "por la trayectoria que describiría [un cuerpo] si... se moviera uniformemente al mismo tiempo ". grado de velocidad con que se mueve en ese instante dado".

Heytesbury y otros determinaron matemáticamente la distancia recorrida por un cuerpo que se somete a un movimiento uniformemente acelerado (hoy resuelto por integración), afirmando que "un cuerpo en movimiento que adquiere o pierde uniformemente ese incremento [de velocidad] recorrerá en algún momento dado una [distancia] completamente igual a la que atravesaría si se moviera continuamente durante el mismo tiempo con el grado medio [de velocidad]".

Nicole Oresme de la Universidad de París y el italiano Giovanni di Casali proporcionaron de forma independiente demostraciones gráficas de esta relación, afirmando que el área debajo de la línea que representa la aceleración constante representaba la distancia total recorrida. En un comentario matemático posterior sobre los Elementos de Euclides, Oresme hizo un análisis general más detallado en el que demostró que un cuerpo adquirirá en cada incremento sucesivo de tiempo un incremento de cualquier cualidad que aumente con los números impares. Como Euclides había demostrado que la suma de los números impares son los números cuadrados, la cualidad total que adquiere el cuerpo aumenta con el cuadrado del tiempo.

Renacimiento

Durante el Renacimiento, el desarrollo de las matemáticas y de la contabilidad se entrelazaron. Si bien no existe una relación directa entre el álgebra y la contabilidad, la enseñanza de las materias y los libros publicados a menudo estaban destinados a los hijos de comerciantes que fueron enviados a escuelas de contabilidad (en Flandes y Alemania) o escuelas de ábaco (conocidas como abbaco en Italia), donde aprendieron las habilidades útiles para el comercio y el comercio. Probablemente no haya necesidad de álgebra para realizar operaciones de contabilidad, pero para operaciones de trueque complejas o el cálculo de interés compuesto, un conocimiento básico de aritmética era obligatorio y el conocimiento de álgebra era muy útil.

Piero della Francesca (c. 1415-1492) escribió libros sobre geometría sólida y perspectiva lineal, incluidos De Prospectiva Pingendi (Sobre la perspectiva para la pintura), Trattato d'Abaco (Tratado del ábaco) y De quinque corporibus regularibus (Sobre los cinco sólidos regulares).

La Summa de Arithmetica, Geometria, Proportioni et Proportionalità de Luca Pacioli (en italiano: "Revisión de aritmética, geometría, razón y proporción") se imprimió y publicó por primera vez en Venecia en 1494. Incluía un tratado de 27 páginas sobre contabilidad, "Particularis de Computis et Scripturis" (en italiano: "Detalles de cálculo y registro"). Fue escrito principalmente y vendido principalmente a comerciantes que utilizaron el libro como texto de referencia, como una fuente de placer de los acertijos matemáticos que contenía y para ayudar a la educación de sus hijos. En Summa Arithmetica, Pacioli introdujo símbolos de más y menos por primera vez en un libro impreso, símbolos que se convirtieron en notación estándar en las matemáticas del Renacimiento italiano.fue también el primer libro conocido impreso en Italia que contenía álgebra. Pacioli obtuvo muchas de sus ideas de Piero Della Francesca a quien plagió.

En Italia, durante la primera mitad del siglo XVI, Scipione del Ferro y Niccolò Fontana Tartaglia descubrieron soluciones para ecuaciones cúbicas. Gerolamo Cardano las publicó en su libro Ars Magna de 1545, junto con una solución para las ecuaciones de cuarto grado, descubierta por su alumno Lodovico Ferrari. En 1572 Rafael Bombelli publicó su L'Algebra en el que mostraba cómo tratar las cantidades imaginarias que podían aparecer en la fórmula de Cardano para resolver ecuaciones cúbicas.

El libro de Simon Stevin De Thiende ('el arte de las décimas'), publicado por primera vez en holandés en 1585, contenía el primer tratamiento sistemático de la notación decimal, que influyó en todo el trabajo posterior sobre el sistema de números reales.

Impulsada por las exigencias de la navegación y la creciente necesidad de mapas precisos de grandes áreas, la trigonometría se convirtió en una rama importante de las matemáticas. Bartholomaeus Pitiscus fue el primero en usar la palabra, publicando su Trigonometria en 1595. La tabla de senos y cosenos de Regiomontanus se publicó en 1533.

Durante el Renacimiento, el deseo de los artistas de representar el mundo natural de forma realista, junto con la filosofía redescubierta de los griegos, llevó a los artistas a estudiar matemáticas. Eran también los ingenieros y arquitectos de la época, por lo que en todo caso tenían necesidad de las matemáticas. El arte de pintar en perspectiva y los desarrollos en geometría que implicaba, fueron estudiados intensamente.

Matemáticas durante la Revolución Científica

Siglo 17

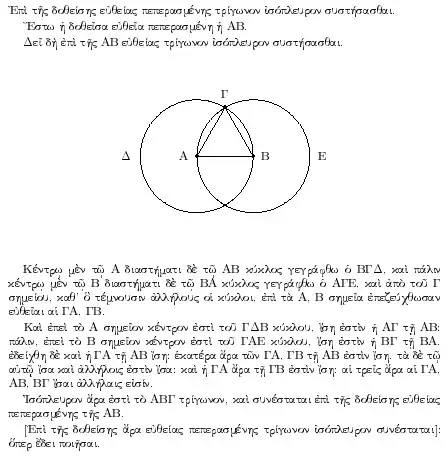
El siglo XVII vio un aumento sin precedentes de ideas matemáticas y científicas en toda Europa. Galileo observó las lunas de Júpiter en órbita alrededor de ese planeta, usando un telescopio basado en un juguete importado de Holanda. Tycho Brahe había reunido una enorme cantidad de datos matemáticos que describían las posiciones de los planetas en el cielo. Por su posición como asistente de Brahe, Johannes Kepler fue expuesto por primera vez e interactuó seriamente con el tema del movimiento planetario. Los cálculos de Kepler se simplificaron con la invención contemporánea de los logaritmos por parte de John Napier y Jost Bürgi. Kepler logró formular leyes matemáticas del movimiento planetario. La geometría analítica desarrollada por René Descartes (1596-1650) permitió trazar esas órbitas en un gráfico, en coordenadas cartesianas.

Sobre la base del trabajo anterior de muchos predecesores, Isaac Newton descubrió las leyes de la física que explican las leyes de Kepler y reunió los conceptos que ahora se conocen como cálculo. Independientemente, Gottfried Wilhelm Leibniz, desarrolló el cálculo y gran parte de la notación del cálculo que todavía se usa en la actualidad. La ciencia y las matemáticas se habían convertido en un esfuerzo internacional, que pronto se extendería por todo el mundo.

Además de la aplicación de las matemáticas a los estudios de los cielos, las matemáticas aplicadas comenzaron a expandirse a nuevas áreas, con la correspondencia de Pierre de Fermat y Blaise Pascal. Pascal y Fermat sentaron las bases para las investigaciones de la teoría de la probabilidad y las reglas correspondientes de la combinatoria en sus discusiones sobre un juego de apuestas. Pascal, con su apuesta, intentó utilizar la teoría de la probabilidad de reciente desarrollo para defender una vida dedicada a la religión, sobre la base de que incluso si la probabilidad de éxito era pequeña, las recompensas eran infinitas. En cierto sentido, esto presagiaba el desarrollo de la teoría de la utilidad en los siglos XVIII y XIX.

Siglo 18

Podría decirse que el matemático más influyente del siglo XVIII fue Leonhard Euler (1707-1783). Sus contribuciones van desde la fundación del estudio de la teoría de grafos con el problema de los Siete Puentes de Königsberg hasta la estandarización de muchos términos y notaciones matemáticas modernas. Por ejemplo, nombró la raíz cuadrada de menos 1 con el símbolo i, y popularizó el uso de la letra griega para representar la relación entre la circunferencia de un círculo y su diámetro. Hizo numerosas contribuciones al estudio de la topología, la teoría de grafos, el cálculo, la combinatoria y el análisis complejo, como lo demuestra la multitud de teoremas y notaciones que llevan su nombre.

Otros matemáticos europeos importantes del siglo XVIII incluyeron a Joseph Louis Lagrange, quien hizo un trabajo pionero en teoría de números, álgebra, cálculo diferencial y cálculo de variaciones, y Laplace, quien, en la era de Napoleón, hizo un trabajo importante sobre los fundamentos del cálculo celeste. mecánica y estadística.

Moderno

Siglo 19

A lo largo del siglo XIX, las matemáticas se volvieron cada vez más abstractas. Carl Friedrich Gauss (1777–1855) personifica esta tendencia. Hizo un trabajo revolucionario en funciones de variables complejas, en geometría y en la convergencia de series, dejando de lado sus muchas contribuciones a la ciencia. También dio las primeras demostraciones satisfactorias del teorema fundamental del álgebra y de la ley de reciprocidad cuadrática.

Este siglo vio el desarrollo de las dos formas de geometría no euclidiana, donde el postulado paralelo de la geometría euclidiana ya no se sostiene. El matemático ruso Nikolai Ivanovich Lobachevsky y su rival, el matemático húngaro János Bolyai, definieron y estudiaron de forma independiente la geometría hiperbólica, donde la singularidad de las paralelas ya no se sostiene. En esta geometría la suma de los ángulos de un triángulo suman menos de 180°. La geometría elíptica fue desarrollada más tarde en el siglo XIX por el matemático alemán Bernhard Riemann; aquí no se puede encontrar ningún paralelo y los ángulos en un triángulo suman más de 180°. Riemann también desarrolló la geometría riemanniana, que unifica y generaliza ampliamente los tres tipos de geometría, y definió el concepto de variedad, que generaliza las ideas de curvas y superficies.

El siglo XIX vio el comienzo de una gran cantidad de álgebra abstracta. Hermann Grassmann en Alemania dio una primera versión de los espacios vectoriales, William Rowan Hamilton en Irlanda desarrolló el álgebra no conmutativa. El matemático británico George Boole ideó un álgebra que pronto se convirtió en lo que ahora se llama álgebra booleana, en la que los únicos números eran el 0 y el 1. El álgebra booleana es el punto de partida de la lógica matemática y tiene aplicaciones importantes en la ingeniería eléctrica y la informática. Augustin-Louis Cauchy, Bernhard Riemann y Karl Weierstrass reformularon el cálculo de manera más rigurosa.

Además, por primera vez, se exploraron los límites de las matemáticas. Niels Henrik Abel, noruego, y Évariste Galois, francés, demostraron que no existe un método algebraico general para resolver ecuaciones polinómicas de grado mayor que cuatro (teorema de Abel-Ruffini). Otros matemáticos del siglo XIX utilizaron esto en sus demostraciones de que la regla y el compás por sí solos no son suficientes para trisecar un ángulo arbitrario, para construir el lado de un cubo dos veces el volumen de un cubo dado, ni para construir un cuadrado de área igual a un dado. círculo. Los matemáticos habían intentado en vano resolver todos estos problemas desde la época de los antiguos griegos. Por otro lado, la limitación de las tres dimensiones en geometría fue superada en el siglo XIX a través de consideraciones de espacio de parámetros y números hipercomplejos.

Las investigaciones de Abel y Galois sobre las soluciones de varias ecuaciones polinómicas sentaron las bases para futuros desarrollos de la teoría de grupos y los campos asociados del álgebra abstracta. En el siglo XX, los físicos y otros científicos vieron en la teoría de grupos la forma ideal de estudiar la simetría.

A finales del siglo XIX, Georg Cantor estableció los primeros fundamentos de la teoría de conjuntos, lo que permitió el tratamiento riguroso de la noción de infinito y se ha convertido en el lenguaje común de casi todas las matemáticas. La teoría de conjuntos de Cantor y el surgimiento de la lógica matemática en manos de Peano, LEJ Brouwer, David Hilbert, Bertrand Russell y AN Whitehead iniciaron un largo debate sobre los fundamentos de las matemáticas.

El siglo XIX vio la fundación de varias sociedades matemáticas nacionales: la London Mathematical Society en 1865, la Société Mathématique de France en 1872, el Circolo Matematico di Palermo en 1884, la Edinburgh Mathematical Society en 1883 y la American Mathematical Society en 1888. La primera sociedad internacional de intereses especiales, la Sociedad Quaternion, se formó en 1899, en el contexto de una controversia sobre vectores.

En 1897, Hensel introdujo los números p-ádicos.

Siglo 20

El siglo XX vio cómo las matemáticas se convertían en una profesión importante. Cada año, se otorgaban miles de nuevos doctorados en matemáticas y había puestos de trabajo disponibles tanto en la enseñanza como en la industria. En la enciclopedia de Klein se emprendió un esfuerzo por catalogar las áreas y aplicaciones de las matemáticas.

En un discurso de 1900 ante el Congreso Internacional de Matemáticos, David Hilbert estableció una lista de 23 problemas matemáticos sin resolver. Estos problemas, que abarcan muchas áreas de las matemáticas, formaron un foco central para gran parte de las matemáticas del siglo XX. A día de hoy, se han resuelto 10, 7 están parcialmente resueltos y 2 siguen abiertos. Los 4 restantes están demasiado vagamente formulados para declararlos resueltos o no.

Conjeturas históricas notables finalmente fueron probadas. En 1976, Wolfgang Haken y Kenneth Appel demostraron el teorema de los cuatro colores, controvertido en ese momento por el uso de una computadora para hacerlo. Andrew Wiles, basándose en el trabajo de otros, demostró el último teorema de Fermat en 1995. Paul Cohen y Kurt Gödel demostraron que la hipótesis del continuo es independiente (no se puede probar ni refutar) de los axiomas estándar de la teoría de conjuntos. En 1998, Thomas Callister Hales demostró la conjetura de Kepler.

Se produjeron colaboraciones matemáticas de un tamaño y alcance sin precedentes. Un ejemplo es la clasificación de grupos simples finitos (también llamado "teorema enorme"), cuya demostración entre 1955 y 2004 requirió 500 artículos de revistas de unos 100 autores y llenó decenas de miles de páginas. Un grupo de matemáticos franceses, incluidos Jean Dieudonné y André Weil, que publicaban bajo el seudónimo de "Nicolas Bourbaki", intentaron exponer todas las matemáticas conocidas como un todo coherente y riguroso. Las varias docenas de volúmenes resultantes han tenido una influencia controvertida en la educación matemática.

La geometría diferencial se hizo realidad cuando Albert Einstein la utilizó en la relatividad general. Áreas completamente nuevas de las matemáticas, como la lógica matemática, la topología y la teoría de juegos de John von Neumann, cambiaron los tipos de preguntas que podían responderse mediante métodos matemáticos. Se abstrajeron todo tipo de estructuras usando axiomas y nombres dados como espacios métricos, espacios topológicos, etc. Como hacen los matemáticos, el concepto de estructura abstracta se abstrajo y condujo a la teoría de categorías. Grothendieck y Serre reformularon la geometría algebraica usando la teoría de la gavilla. Se lograron grandes avances en el estudio cualitativo de los sistemas dinámicos que Poincaré había iniciado en la década de 1890. La teoría de la medida se desarrolló a finales del siglo XIX y principios del XX. Las aplicaciones de medidas incluyen la integral de Lebesgue, Kolmogorov' s axiomatización de la teoría de la probabilidad y la teoría ergódica. La teoría del nudo se amplió enormemente. La mecánica cuántica condujo al desarrollo del análisis funcional. Otras áreas nuevas incluyen la teoría de la distribución de Laurent Schwartz, la teoría del punto fijo, la teoría de la singularidad y la teoría de catástrofes de René Thom, la teoría de modelos y los fractales de Mandelbrot. La teoría de mentiras con sus grupos de mentiras y álgebras de mentiras se convirtió en una de las principales áreas de estudio.

El análisis no estándar, introducido por Abraham Robinson, rehabilitó el enfoque infinitesimal del cálculo, que había caído en descrédito a favor de la teoría de los límites, al extender el campo de los números reales a los números hiperreales que incluyen cantidades infinitesimales e infinitas. Un sistema numérico aún más grande, los números surrealistas fueron descubiertos por John Horton Conway en relación con los juegos combinatorios.

El desarrollo y la mejora continua de las computadoras, al principio máquinas analógicas mecánicas y luego máquinas electrónicas digitales, permitieron que la industria manejara cantidades cada vez mayores de datos para facilitar la producción, distribución y comunicación en masa, y se desarrollaron nuevas áreas de las matemáticas para lidiar con esto.: Teoría de la computabilidad de Alan Turing; teoría de la complejidad; el uso de ENIAC por parte de Derrick Henry Lehmer para promover la teoría de números y la prueba de Lucas-Lehmer; la teoría de la función recursiva de Rózsa Péter; la teoría de la información de Claude Shannon; procesamiento de la señal; análisis de los datos; optimización y otras áreas de la investigación de operaciones. En los siglos anteriores, gran parte del enfoque matemático se centró en el cálculo y las funciones continuas, pero el surgimiento de las redes informáticas y de comunicación condujo a una creciente importancia de los conceptos discretos y la expansión de la combinatoria, incluida la teoría de grafos. La velocidad y la capacidad de procesamiento de datos de las computadoras también permitieron el manejo de problemas matemáticos que requerían demasiado tiempo para resolverlos con cálculos con lápiz y papel, lo que llevó a áreas como el análisis numérico y el cálculo simbólico. Algunos de los métodos y algoritmos más importantes del siglo XX son: el algoritmo simplex, la transformada rápida de Fourier, los códigos correctores de errores, el filtro de Kalman de la teoría de control y el algoritmo RSA de criptografía de clave pública. La velocidad y la capacidad de procesamiento de datos de las computadoras también permitieron el manejo de problemas matemáticos que requerían demasiado tiempo para resolverlos con cálculos con lápiz y papel, lo que llevó a áreas como el análisis numérico y el cálculo simbólico. Algunos de los métodos y algoritmos más importantes del siglo XX son: el algoritmo simplex, la transformada rápida de Fourier, los códigos correctores de errores, el filtro de Kalman de la teoría de control y el algoritmo RSA de criptografía de clave pública. La velocidad y la capacidad de procesamiento de datos de las computadoras también permitieron el manejo de problemas matemáticos que requerían demasiado tiempo para resolverlos con cálculos con lápiz y papel, lo que llevó a áreas como el análisis numérico y el cálculo simbólico. Algunos de los métodos y algoritmos más importantes del siglo XX son: el algoritmo simplex, la transformada rápida de Fourier, los códigos correctores de errores, el filtro de Kalman de la teoría de control y el algoritmo RSA de criptografía de clave pública.

Al mismo tiempo, se realizaron reflexiones profundas sobre las limitaciones de las matemáticas. En 1929 y 1930 se demostró que la verdad o falsedad de todos los enunciados formulados sobre los números naturales más la suma o la multiplicación (pero no ambas), era decidible, es decir, podía determinarse mediante algún algoritmo. En 1931, Kurt Gödel descubrió que este no era el caso de los números naturales más la suma y la multiplicación; este sistema, conocido como aritmética de Peano, era de hecho incompletable. (La aritmética de Peano es adecuada para gran parte de la teoría de números, incluida la noción de número primo). Una consecuencia de los dos teoremas de incompletud de Gödel es que en cualquier sistema matemático que incluya la aritmética de Peano (incluido todo el análisis y la geometría), la verdad necesariamente supera prueba, es decir, hay enunciados verdaderos que no pueden probarse dentro del sistema.

Una de las figuras más pintorescas de las matemáticas del siglo XX fue Srinivasa Aiyangar Ramanujan (1887-1920), un autodidacta indio que conjeturó o probó más de 3000 teoremas, incluidas las propiedades de números altamente compuestos, la función de partición y sus asintóticas, y funciones theta simuladas.. También realizó importantes investigaciones en las áreas de funciones gamma, formas modulares, series divergentes, series hipergeométricas y teoría de números primos.

Paul Erdős publicó más artículos que cualquier otro matemático en la historia, trabajando con cientos de colaboradores. Los matemáticos tienen un juego equivalente al Juego de Kevin Bacon, que conduce al número de Erdős de un matemático. Esto describe la "distancia de colaboración" entre una persona y Erdős, medida por la autoría conjunta de artículos matemáticos.

Emmy Noether ha sido descrita por muchos como la mujer más importante en la historia de las matemáticas. Estudió las teorías de anillos, campos y álgebras.

Como en la mayoría de las áreas de estudio, la explosión del conocimiento en la era científica ha llevado a la especialización: a finales de siglo había cientos de áreas especializadas en matemáticas y la Clasificación de Materias Matemáticas tenía decenas de páginas. Se publicaron más y más revistas matemáticas y, a finales de siglo, el desarrollo de la World Wide Web condujo a la publicación en línea.

Siglo 21

En 2000, el Clay Mathematics Institute anunció los siete Problemas del Premio del Milenio, y en 2003 la conjetura de Poincaré fue resuelta por Grigori Perelman (quien se negó a aceptar un premio, ya que era crítico con el sistema matemático).

La mayoría de las revistas matemáticas ahora tienen versiones en línea, así como versiones impresas, y se lanzan muchas revistas solo en línea. Hay un impulso cada vez mayor hacia la publicación de acceso abierto, popularizado por primera vez por arXiv.

Futuro

Hay muchas tendencias observables en matemáticas, la más notable es que el tema es cada vez más amplio, las computadoras son cada vez más importantes y poderosas, la aplicación de las matemáticas a la bioinformática se está expandiendo rápidamente y el volumen de datos producido por la ciencia y la industria, facilitada por las computadoras, se está expandiendo exponencialmente.