Hexágono

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Forma con seis lados

En geometría, un hexágono (del griego ἕξ, hex, que significa "seis", y γωνία, gonía, que significa "esquina, ángulo") o sexágono (del latín sexcode: lat promovido a code: la , que significa "seis") es un polígono de seis lados o 6-gon que crea el contorno de un cubo. El total de los ángulos internos de cualquier hexágono simple (que no se corte a sí mismo) es 720°.

Hexágono normal

Un hexágono regular tiene el símbolo de Schläfli {6} y también se puede construir como un triángulo equilátero truncado, t{3}, que alterna dos tipos de aristas.

Una animación paso a paso de la construcción de un hexágono regular utilizando brújula y rectitud, dada por Euclides Elementos, Libro IV, Proposición 15: esto es posible como 6

=

2 × 3, un producto de un poder de dos y diferentes primos de Fermat.

Cuando la longitud lateral AB se da, dibujando un arco circular desde el punto A y el punto B da la intersección M, el centro del círculo circunscrito. Transfiera el segmento de línea AB cuatro veces en el círculo circunscrito y conectar los puntos de la esquina.

Un hexágono regular se define como un hexágono que es tanto equilátero como equiángulo. Es bicéntrico, lo que significa que es cíclico (tiene un círculo circunscrito) y tangencial (tiene un círculo inscrito).

La longitud común de los lados iguala el radio del círculo circunscrito o el círculo circunscrito, que equivale a ${displaystyle {tfrac {2}{sqrt {3}}}}$ tiempos el apothem (radius del círculo inscrito). Todos los ángulos internos son de 120 grados. Un hexágono regular tiene seis simetrías rotativas (simetría rotacional del orden seis) y seis simetrías de reflexión (seis líneas de simetría), conformando el grupo dihedral D₆. Las diagonales más largas de un hexágono regular, que conecta vértices diametralmente opuestos, son dos veces la longitud de un lado. De esto se puede ver que un triángulo con un vértice en el centro del hexágono regular y compartir un lado con el hexágono es equilátero, y que el hexágono regular se puede dividir en seis triángulos equiláteros.

Al igual que los cuadrados y los triángulos equiláteros, los hexágonos regulares encajan entre sí sin espacios para mosacular el plano (tres hexágonos que se unen en cada vértice), por lo que son útiles para construir mosaicos. Las celdas de un panal de colmena son hexagonales por esta razón y porque la forma hace un uso eficiente del espacio y los materiales de construcción. El diagrama de Voronoi de una red triangular regular es la teselación de panal de hexágonos. No se suele considerar un triambus, aunque es equilátero.

Parámetros

El diámetro máximo (que corresponde a la diagonal mayor del hexágono), D, es el doble del radio máximo o circunradio, R, que es igual a la longitud del lado, t. El diámetro mínimo o el diámetro de la circunferencia inscrita (separación de lados paralelos, distancia entre planos, diagonal corta o altura cuando descansa sobre una base plana), d, es el doble del radio mínimo o en el radio, r. Los máximos y mínimos están relacionados por el mismo factor:

{displaystyle {frac {1}{2}}d=r=cos(30^{circ })R={frac {sqrt {3}}{2}}R={frac {sqrt {3}}{2}}t}

y, de manera similar,

{displaystyle d={frac {sqrt {3}}{2}}D.}

El área de un hexágono regular

{displaystyle {begin{aligned}A&={frac {3{sqrt {3}}}{2}}R^{2}=3Rr=2{sqrt {3}}r^{2}\[3pt]&={frac {3{sqrt {3}}}{8}}D^{2}={frac {3}{4}}Dd={frac {sqrt {3}}{2}}d^{2}\[3pt]&approx 2.598R^{2}approx 3.464r^{2}\&approx 0.6495D^{2}approx 0.866d^{2}.end{aligned}}}

Para cualquier polígono regular, el área también se puede expresar en términos del apothem a y el perímetro p. Para el hexágono regular estos son dados por a = r, y p ${displaystyle {}=6R=4r{sqrt {3}}}$ Así que

{displaystyle {begin{aligned}A&={frac {ap}{2}}\&={frac {rcdot 4r{sqrt {3}}}{2}}=2r^{2}{sqrt {3}}\&approx 3.464r^{2}.end{aligned}}}

El hexágono regular llena la fracción ${displaystyle {tfrac {3{sqrt {3}}}{2pi }}approx 0.8270}$ de su círculo circunscrito.

Si un hexágono regular tiene vértices sucesivos A, B, C, D, E, F y si P es cualquier punto del círculo entre B y C, entonces PE + PF = PA + PB + PC + PD.

De la relación entre el circunradio y el interior del radio se deduce que la relación entre la altura y el ancho de un hexágono regular es 1:1,1547005; es decir, un hexágono con una diagonal larga de 1.0000000 tendrá una distancia de 0.8660254 entre lados paralelos.

Punto en el plano

Para un punto arbitrario en el plano de un hexágono regular con circunradius $R$ , cuyas distancias al centroide del hexágono regular y sus seis vértices son $L$ y $d_{i}$ respectivamente, tenemos

{displaystyle d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2left(R^{2}+L^{2}right),}

{displaystyle d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3left(R^{2}+L^{2}right),}

{displaystyle d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3left(left(R^{2}+L^{2}right)^{2}+2R^{2}L^{2}right).}

Si $d_{i}$ son las distancias de los vértices de un hexágono regular a cualquier punto en su círculo, entonces

{displaystyle left(sum _{i=1}^{6}d_{i}^{2}right)^{2}=4sum _{i=1}^{6}d_{i}^{4}.}

Simetría

Hexágonos de ejemplo por simetría

d6 isotoxal	g6 Dirigida	p6 isogonal		d2	g2 general paralelaogon	p2
	r12 ordinario				i4
	g3				a1

Las seis líneas de reflexión de un hexágono regular, con Dih₆ o r12 simetría, orden 12.

Las simetrías dihedral se dividen dependiendo de si pasan a través de vértices (d para diagonal) o bordes (p para perpendiculares) Simetrías cíclicas en la columna media se etiquetan como g por sus órdenes centrales de giro. Simetría completa de la forma regular es r12 y ninguna simetría está etiquetada a1.

El hexágono regular tiene simetría D₆. Hay 16 subgrupos. Hay 8 hasta el isomorfismo: sí mismo (D₆), 2 diedros: (D_3, D₂), 4 cíclicos: (Z ₆, Z₃, Z₂, Z₁) y el trivial (e)

Estas simetrías expresan nueve simetrías distintas de un hexágono regular. John Conway los etiqueta con una letra y un orden de grupo. r12 es simetría total y a1 no es simetría. p6, un hexágono isogonal construido por tres espejos que pueden alternar aristas largas y cortas, y d6, un hexágono isotoxal construido con la misma longitud de aristas, pero con vértices que alternan dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del hexágono regular. Las formas i4 son hexágonos regulares aplanados o estirados a lo largo de una dirección de simetría. Puede verse como un rombo alargado, mientras que d2 y p2 pueden verse como cometas alargadas horizontal y verticalmente. Los hexágonos g2, con lados opuestos paralelos, también se denominan paralelógonos hexagonales.

Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Solo el subgrupo g6 no tiene grados de libertad pero puede verse como aristas dirigidas.

Los hexágonos de simetría g2, i4 y r12, como los paralelogonos, pueden teselar el plano euclidiano por traslación. Otras formas hexagonales pueden teselar el plano con diferentes orientaciones.

p6m (*632)	cmm (2*22)	p2 (2222)	p31m (3*3)	(22*)		pg (××)
r12	i4	g2	d2	d2	p2	a1
Dih₆	Dih₂	Z₂	Dih₁			Z₁

Grupos A2 y G2

A2 grupo raíces	G2 grupo raíces

Las 6 raíces del sencillo grupo Lie A2, representado por un diagrama Dynkin , están en un patrón hexagonal regular. Las dos raíces simples tienen un ángulo de 120° entre ellas.

Las 12 raíces del grupo Excepcional Lie G2, representado por un diagrama Dynkin están también en un patrón hexagonal. Las dos raíces simples de dos longitudes tienen un ángulo de 150° entre ellas.

Disección

Proyección de 6 cachorros	12 romb disección

Coxeter afirma que cada zonogon (un gon de 2m cuyos lados opuestos son paralelos y de igual longitud) se puede dividir en 1⁄2m(m − 1) paralelogramos. En particular, esto es cierto para polígonos regulares con muchos lados iguales, en cuyo caso los paralelogramos son todos rombos. Esta descomposición de un hexágono regular se basa en una proyección poligonal de Petrie de un cubo, con 3 de 6 caras cuadradas. Otros paralelogonos y direcciones proyectivas del cubo se diseccionan dentro de cuboides rectangulares.

Disección de hexágonos en tres rombos y paralelogramas
2D	Rhombs	Parallelogramas

	Recursos ordinarios {6}	paralelogones hexagonales
3D	Caras cuadradas		Caras rectangulares

	Cube		Cuboide rectangular

Polígonos y mosaicos relacionados

Un hexágono regular tiene el símbolo de Schläfli {6}. Un hexágono regular es una parte del teselado hexagonal regular, {6,3}, con tres caras hexagonales alrededor de cada vértice.

También se puede crear un hexágono regular como un triángulo equilátero truncado, con el símbolo de Schläfli t{3}. Vista con dos tipos (colores) de bordes, esta forma solo tiene simetría D₃.

Un hexágono truncado, t{6}, es un dodecágono, {12}, alternando dos tipos (colores) de aristas. Un hexágono alterno, h{6}, es un triángulo equilátero, {3}. Un hexágono regular se puede estrellar con triángulos equiláteros en sus bordes, creando un hexagrama. Un hexágono regular se puede dividir en seis triángulos equiláteros agregando un punto central. Este patrón se repite dentro del mosaico triangular regular.

Un hexágono regular se puede extender a un dodecágono regular agregando cuadrados alternos y triángulos equiláteros a su alrededor. Este patrón se repite dentro del mosaico rombitrihexagonal.

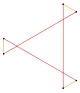Recursos ordinarios {6}	Truncado t{3} = {6}	triángulos hipertruncados			Stellated Figura estrella 2{3}	Truncado t{6} = {12}	Suplente h{6} = {3}

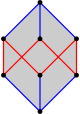Crossed hexagon	Un hexágono cóncavo	Un hexágono autointersecante (pológono estrella)	Extended Central {6} en {12}	Un hexágono en el cubo	Diseccionado {6}	proyección octaedro	Gráfico completo

Hexágonos autocruzados

Hay seis hexágonos que se cruzan a sí mismos con la disposición de vértice del hexágono regular:

Hexágonos autointersecantes con vértices regulares
Dih₂			Dih₁		Dih₃
Gráfico 8	Center-flip	Unicursal	Pescado	Doble cola	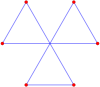Triple-tail

Estructuras hexagonales

Cierre de la autopista gigante

De las abejas' panales a la Calzada del Gigante, los patrones hexagonales prevalecen en la naturaleza debido a su eficiencia. En una cuadrícula hexagonal, cada línea es lo más corta posible si se va a llenar un área grande con la menor cantidad de hexágonos. Esto significa que los panales requieren menos cera para construirse y ganan mucha fuerza bajo compresión.

Los hexágonos irregulares con aristas opuestas paralelas se denominan paralelogonos y también pueden teselar el plano por traslación. En tres dimensiones, los prismas hexagonales con caras opuestas paralelas se denominan paraleloedros y estos pueden teselar 3 espacios por traslación.

Tessellations del prisma hexagonal
Formulario	Tiro hexagonal	Miel prismático hexagonalb
Recursos ordinarios
Parallelogonal

Teselados por hexágonos

Además del hexágono regular, que determina una teselación única del plano, cualquier hexágono irregular que satisfaga el criterio de Conway teselará el plano.

Hexágono inscrito en una sección cónica

El teorema de Pascal (también conocido como el "Teorema de Hexagrammum Mysticum") establece que si un hexágono arbitrario se inscribe en cualquier sección cónica, y los pares de lados opuestos se extienden hasta que se encuentran, el tres puntos de intersección estarán en una línea recta, la "línea de Pascal" de esa configuración.

Hexágono cíclico

El hexágono de Lemoine es un hexágono cíclico (inscrito en un círculo) con vértices dados por las seis intersecciones de las aristas de un triángulo y las tres rectas paralelas a las aristas que pasan por su punto simediano.

Si los lados sucesivos de un hexágono cíclico son a, b, c, d, e, f, entonces las tres diagonales principales se cruzan en un solo punto si y solo si ace = bdf.

Si, para cada lado de un hexágono cíclico, los lados adyacentes se extienden hasta su intersección, formando un triángulo exterior al lado dado, entonces los segmentos que conectan los circuncentros de triángulos opuestos son concurrentes.

Si un hexágono tiene vértices en el círculo circunscrito de un triángulo acutángulo en los seis puntos (incluidos los tres vértices del triángulo) donde las altitudes extendidas del triángulo se encuentran con el círculo circunscrito, entonces el área del hexágono es el doble del área del triángulo.

Hexágono tangencial a una sección cónica

Sea ABCDEF un hexágono formado por seis rectas tangentes de una sección cónica. Luego, el teorema de Brianchon establece que las tres diagonales principales AD, BE y CF se cortan en un solo punto.

En un hexágono que es tangencial a un círculo y que tiene lados consecutivos a, b, c, d, e y f,

{displaystyle a+c+e=b+d+f.}

Triángulos equiláteros en los lados de un hexágono arbitrario

triángulos equiláteros en los lados de un hexágono arbitrario

Si un triángulo equilátero se construye externamente en cada lado de cualquier hexágono, entonces los puntos medios de los segmentos que conectan los centroides de triángulos opuestos forman otro triángulo equilátero.

Hexágono sesgado

Un hexágono skew regular visto como bordes (negro) de un antiprisma triangular, simetría D_3d, [2]⁺,6], (2*3), orden 12.

Un hexágono sesgado es un polígono sesgado con seis vértices y aristas pero que no existe en el mismo plano. El interior de tal hexágono generalmente no está definido. Un hexágono en zig-zag sesgado tiene vértices que se alternan entre dos planos paralelos.

Un hexágono sesgado regular es de vértice transitivo con longitudes de borde iguales. En tres dimensiones será un hexágono sesgado en zig-zag y se puede ver en los vértices y aristas laterales de un antiprisma triangular con el mismo D_3d, [2⁺, 6] simetría, orden 12.

El cubo y el octaedro (igual que el antiprisma triangular) tienen hexágonos oblicuos regulares como polígonos de Petrie.

Hexágonos Skew en 3 ejes
Cube	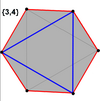Octahedron

Polígonos de Petrie

El hexágono oblicuo regular es el polígono de Petrie para estos poliedros y politopos regulares, uniformes y duales de dimensión superior, que se muestran en estas proyecciones ortogonales oblicuas:

4D		5D
3-3 duoprismo	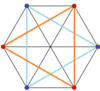3-3 duopyramid	5-simplex

Hexágono equilátero convexo

Una diagonal principal de un hexágono es una diagonal que divide el hexágono en cuadriláteros. En todo hexágono equilátero convexo (uno con todos los lados iguales) con lado común a, existe una diagonal principal d₁ tal que

frac{d_1}{a} leq 2

y una diagonal principal d₂ tal que

{sqrt {3}}.}" xmlns="http://www.w3.org/1998/Math/MathML">d2a■3.{fnMicroc} {fnK} {fn} {fnK}} {f}}} {f}}} {f}}}} {f}}}}} {f}}}}}} {fn}}}}} {fn}}}}}}}} {f}}}}}} {f}}}}}}}}}}}}} { {3}} sqrt{3}." aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/257045418872783c5d314dde920830bce569c076" style="vertical-align: -1.838ex; width:9.943ex; height:5.343ex;"/>

Poliedros con hexágonos

No hay sólido platónico hecho de sólo hexágonos regulares, porque los hexágonos tessellate, no permitiendo que el resultado se "enrolle". Los sólidos arquimedes con algunas caras hexagonales son el tetraedro truncado, octaedro truncado, icosahedro truncado (de bola de fútbol y fama de fullereno), cuboctaedro truncado y el icosidodecahedro truncado. Estos hexágonos pueden considerarse triángulos truncados, con diagramas de Coxeter de la forma y .

Hexagons in Archimedean solids
Tetraedral	Octahedral		Icosahedral

truncated tetrahedron	truncado octaedro	truncated cuboctahedron	icosahedron truncado	icosidodecedro truncado

Hay otros poliedros de simetría con hexágonos estirados o aplanados, como estos poliedros de Goldberg G(2,0):

Hexagons in Goldberg polyhedra
Tetraedral	Octahedral	Icosahedral
Chamferedron	Cubo de Chamfer	Chamfered dodecahedron

También hay 9 sólidos de Johnson con hexágonos regulares:

sólidos Johnson con hexágonos
cúpula triangular	cúpula triangular alargada	glyroelongated triangular cupola
prisma hexagonal aumentado	parabiaugmentado hexagonal prism	prismo hexagonal metabiaugmentado	prisma hexagonal triaugmentado
aumentada tetraedro truncado	hebesphenorotunda triangular	Truncated triakis tetrahedron

Prismoids with hexagons
Prisma hexagonal	Antiprisma hexagonal	pirámide hexagonal

Tilings con hexágonos regulares
Recursos ordinarios	1-uniform
{6,3}	r{6,3}	rr{6,3}	tr{6,3}

2-uniform tilings

Galería de hexágonos naturales y artificiales

La estructura cristalina ideal del grafeno es una rejilla hexagonal.
segmentos de espejo de E-ELT
Un panal de miel colmena
Los cortes del carapace de una tortuga
Hexágono de Saturno, un patrón de nubes hexagonales alrededor del polo norte del planeta
Micrograph of a snowflake
Benzene, el compuesto aromático más simple con forma hexagonal.
Orden hexagonal de burbujas en una espuma.
Estructura de cristal de un hexágono molecular compuesto por anillos aromáticos hexagonales.
$Naturally formed basalt columns from Giant's Causeway in Northern Ireland; large masses must cool slowly to form a polygonal fracture pattern$
Columnas de basalto naturalmente formadas de la Causa Giant en Irlanda del Norte; las masas grandes deben enfriarse lentamente para formar un patrón de fractura poligonal
Una vista aérea de Fort Jefferson en el Parque Nacional Dry Tortugas
El espejo del telescopio espacial James Webb está compuesto por 18 segmentos hexagonales.
Metropolitan France tiene una forma vagamente hexagonal. En francés, l'Hexagone se refiere al continente europeo de Francia.
Cristal hexagonal Hanksite, uno de los muchos minerales del sistema de cristal hexagonal
Granero hexagonal
El Hexagonal, teatro hexagonal en Reading, Berkshire
El ajedrez hexagonal de Władysław Gliński
Pabellón en los jardines botánicos de Taiwán
Ventana hexagonal

Contenido relacionado

Más resultados...