Historia de la notación matemática

La historia de la notación matemática incluye el comienzo, el progreso y la difusión cultural de los símbolos matemáticos y el conflicto de los métodos de notación enfrentados en el movimiento de una notación hacia la popularidad o la desapercibición. La notación matemática comprende los símbolos utilizados para escribir ecuaciones y fórmulas matemáticas. La notación generalmente implica un conjunto de representaciones bien definidas de operadores de cantidades y símbolos. La historia incluye números arábigos hindúes, letras de los alfabetos romano, griego, hebreo y alemán, y una gran cantidad de símbolos inventados por matemáticos durante los últimos siglos.

El desarrollo de la notación matemática se puede dividir en etapas. La etapa " retórica " ​​es donde los cálculos se realizan con palabras y no se utilizan símbolos. La etapa " sincopada " es donde las operaciones y cantidades de uso frecuente se representan mediante abreviaturas sintácticas simbólicas. Desde la antigüedad hasta la era posclásica, los estallidos de creatividad matemática a menudo fueron seguidos por siglos de estancamiento. Cuando se abrió la era moderna y comenzó la difusión mundial del conocimiento, salieron a la luz ejemplos escritos de desarrollos matemáticos. El " simbólico"Etapa es donde los sistemas integrales de notación reemplazan a la retórica. A partir de Italia en el siglo XVI, se realizaron nuevos desarrollos matemáticos, interactuando con nuevos descubrimientos científicos, a un ritmo creciente que continúa hasta el día de hoy. Este sistema simbólico fue utilizado por medieval matemáticos indios y en Europa desde mediados del siglo XVII, y ha seguido desarrollándose en la era contemporánea.

El área de estudio conocida como historia de las matemáticas es principalmente una investigación sobre el origen de los descubrimientos en matemáticas y, el enfoque aquí, la investigación sobre los métodos matemáticos y la notación del pasado.

Etapa retórica

Aunque la historia comienza con la de las escuelas jónicas, no hay duda de que los antiguos griegos que le prestaron atención estaban en gran parte en deuda con las investigaciones previas de los antiguos egipcios y los antiguos fenicios. La característica distintiva de la notación numérica, es decir, los símbolos que tienen valores tanto locales como intrínsecos (aritmética), implica un estado de civilización en el período de su invención. Nuestro conocimiento de los logros matemáticos de estos primeros pueblos, a los que está dedicada esta sección, es imperfecto y las breves notas siguientes deben considerarse como un resumen de las conclusiones que parecen más probables, y la historia de las matemáticas comienza con las secciones simbólicas.

Muchas áreas de las matemáticas comenzaron con el estudio de problemas del mundo real, antes de que las reglas y conceptos subyacentes fueran identificados y definidos como estructuras abstractas. Por ejemplo, la geometría tiene su origen en el cálculo de distancias y áreas en el mundo real; el álgebra comenzó con métodos para resolver problemas de aritmética.

No puede haber duda de que la mayoría de los pueblos primitivos que han dejado registros sabían algo de numeración y mecánica, y que unos pocos también estaban familiarizados con los elementos de la agrimensura. En particular, los egipcios prestaron atención a la geometría y los números, y los fenicios a la aritmética práctica, la contabilidad, la navegación y la agrimensura. Los resultados obtenidos por estas personas parecen haber sido accesibles, bajo ciertas condiciones, a los viajeros. Es probable que el conocimiento de los egipcios y fenicios fuera en gran parte el resultado de la observación y la medición, y representara la experiencia acumulada de muchas eras.

Comienzo de la notación

Las matemáticas escritas comenzaron con números expresados ​​como marcas de conteo, y cada conteo representaba una sola unidad. Los símbolos numéricos consistían probablemente en trazos o muescas cortadas en madera o piedra, e inteligibles por igual para todas las naciones. Por ejemplo, una muesca en un hueso representaba un animal, una persona o cualquier otra cosa. Los pueblos con los que los griegos de Asia Menor (entre los que comienza la notación en la historia occidental) probablemente entraron en contacto frecuente eran los que habitaban el litoral oriental del Mediterráneo: y la tradición griega asignó uniformemente el desarrollo especial de la geometría a los egipcios, y el de la ciencia de los números tanto para los egipcios como para los fenicios.

Los antiguos egipcios tenían una notación simbólica que era la numeración por jeroglíficos.Las matemáticas egipcias tenían un símbolo para uno, diez, cien, mil, diez mil, cien mil y un millón. Los dígitos más pequeños se colocaron a la izquierda del número, ya que están en números arábigos hindúes. Más tarde, los egipcios usaron escritura hierática en lugar de jeroglífica para mostrar números. Hierático era más como cursivo y reemplazó varios grupos de símbolos con los individuales. Por ejemplo, las cuatro líneas verticales utilizadas para representar cuatro fueron reemplazadas por una sola línea horizontal. Esto se encuentra en el Papiro matemático de Rhind (c. 2000-1800 a. C.) y el Papiro matemático de Moscú (c. 1890 a. C.). El sistema que utilizaron los egipcios fue descubierto y modificado por muchas otras civilizaciones del Mediterráneo. Los egipcios también tenían símbolos para las operaciones básicas: las piernas que avanzaban representaban la suma,

Los mesopotámicos tenían símbolos para cada potencia de diez. Más tarde, escribieron sus números casi exactamente de la misma manera que se hace en los tiempos modernos. En lugar de tener símbolos para cada potencia de diez, simplemente pondrían el coeficiente de ese número. Cada dígito estaba separado solo por un espacio, pero en la época de Alejandro Magno, habían creado un símbolo que representaba el cero y era un marcador de posición. Los mesopotámicos también usaron un sistema sexagesimal, es decir, base sesenta. Es este sistema el que se usa en los tiempos modernos cuando se mide el tiempo y los ángulos. Las matemáticas babilónicas se derivan de más de 400 tablillas de arcilla desenterradas desde la década de 1850.Escritas en escritura cuneiforme, las tablillas se inscribían mientras la arcilla estaba húmeda y se horneaban en un horno o al calor del sol. Algunos de estos parecen ser tareas calificadas. La evidencia más antigua de las matemáticas escritas se remonta a los antiguos sumerios y al sistema de metrología del 3000 a. Desde alrededor del 2500 a. C. en adelante, los sumerios escribieron tablas de multiplicar en tablillas de arcilla y se ocuparon de ejercicios geométricos y problemas de división. Los primeros rastros de los números babilónicos también se remontan a este período.

La mayoría de las tablillas de arcilla mesopotámicas datan de 1800 a 1600 aC y cubren temas que incluyen fracciones, álgebra, ecuaciones cuadráticas y cúbicas, y el cálculo de pares regulares, recíprocos y. Las tabletas también incluyen tablas de multiplicar y métodos para resolver ecuaciones lineales y cuadráticas. La tablilla babilónica YBC 7289 da una aproximación de √ 2con precisión de cinco decimales. Las matemáticas babilónicas se escribieron utilizando un sistema numérico sexagesimal (base 60). De esto se deriva el uso moderno de 60 segundos en un minuto, 60 minutos en una hora y 360 (60 × 6) grados en un círculo, así como el uso de minutos y segundos de arco para indicar fracciones de un grado.. Los avances babilónicos en matemáticas se vieron facilitados por el hecho de que 60 tiene muchos divisores: el recíproco de cualquier número entero que sea un múltiplo de divisores de 60 tiene una expansión finita en base 60. (En aritmética decimal, solo los recíprocos de múltiplos de 2 y 5 tienen expansiones decimales finitas). Además, a diferencia de los egipcios, griegos y romanos, los babilonios tenían un verdadero sistema de valor posicional, donde los dígitos escritos en la columna izquierda representaban valores más grandes, como en el sistema decimal. Les faltaba, sin embargo,

Etapa sincopada

La historia de las matemáticas no puede remontarse con certeza a ninguna escuela o período anterior a la de los griegos jónicos, pero la historia subsiguiente puede dividirse en períodos, cuyas distinciones entre los cuales están bastante bien marcadas. Las matemáticas griegas, que se originaron con el estudio de la geometría, tendieron desde sus comienzos a ser deductivas y científicas. Desde el siglo IV d. C., comúnmente se le ha dado crédito a Pitágoras por descubrir el teorema de Pitágoras, un teorema en geometría que establece que en un triángulo rectángulo, el área del cuadrado en la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados de los otros dos lados.Los textos matemáticos antiguos están disponibles con la notación del Antiguo Egipto mencionada anteriormente y con Plimpton 322 (matemáticas babilónicas c. 1900 a. C.). El estudio de las matemáticas como materia por derecho propio comienza en el siglo VI a. C. con los pitagóricos, quienes acuñaron el término "matemáticas" del griego antiguo μάθημα (matema), que significa "materia de instrucción".

La influencia de Platón ha sido especialmente fuerte en las matemáticas y las ciencias. Ayudó a distinguir entre matemáticas puras y aplicadas ampliando la brecha entre la "aritmética", ahora llamada teoría de números y la "logística", ahora llamada aritmética. Las matemáticas griegas refinaron en gran medida los métodos (especialmente a través de la introducción del razonamiento deductivo y el rigor matemático en las pruebas) y ampliaron el tema de las matemáticas. A Aristóteles se le atribuye lo que más tarde se llamaría la ley del tercero excluido.

Matemática abstracta es lo que trata de la magnitud o cantidad, conferida absoluta y generalmente, sin tener en cuenta ninguna especie de magnitud particular, como la aritmética y la geometría. En este sentido, la matemática abstracta se opone a la matemática mixta, en donde las propiedades simples y abstractas, y las relaciones de cantidades consideradas primitivamente en matemáticas, se aplican a objetos sensibles, y por ese medio se entremezclan con consideraciones físicas, como en hidrostática, óptica y navegación.

Generalmente se considera que Arquímedes es el matemático más grande de la antigüedad y uno de los más grandes de todos los tiempos. Usó el método de agotamiento para calcular el área bajo el arco de una parábola con la suma de una serie infinita y dio una aproximación notablemente precisa de pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de superficies de revolución y un ingenioso sistema para expresar números muy grandes.

En el desarrollo histórico de la geometría, los antiguos griegos dieron los pasos en la abstracción de la geometría. Los Elementos de Euclides son la documentación más antigua existente de los axiomas de la geometría plana, aunque Proclo habla de una axiomatización anterior de Hipócrates de Quíos. Los Elementos de Euclides (c. 300 a. C.) es uno de los tratados matemáticos griegos más antiguos que existen y consta de 13 libros escritos en Alejandría; recopilando teoremas probados por otros matemáticos, complementados con algún trabajo original.El documento es una exitosa colección de definiciones, postulados (axiomas), proposiciones (teoremas y construcciones) y pruebas matemáticas de las proposiciones. El primer teorema de Euclides es un lema que posee propiedades de los números primos. Los trece libros influyentes cubren la geometría euclidiana, el álgebra geométrica y la versión griega antigua de los sistemas algebraicos y la teoría elemental de los números. Fue omnipresente en el Quadrivium y es fundamental en el desarrollo de la lógica, las matemáticas y la ciencia.

Diofanto de Alejandría fue autor de una serie de libros llamados Arithmetica, muchos de los cuales ahora se han perdido. Estos textos tratan sobre la resolución de ecuaciones algebraicas. Boecio proporcionó un lugar para las matemáticas en el plan de estudios en el siglo VI cuando acuñó el término quadrivium para describir el estudio de la aritmética, la geometría, la astronomía y la música. Escribió De Institutione arithmetica, una traducción libre del griego de la Introducción a la aritmética de Nicómaco; De Institutione musica, también derivada de fuentes griegas; y una serie de extractos de los Elementos de Euclides. Sus obras eran más teóricas que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.

Numeración acrofónica y milesia

Los griegos empleaban la numeración ática, que se basaba en el sistema de los egipcios y luego fue adaptado y utilizado por los romanos. Los números griegos del uno al cuatro eran líneas verticales, como en los jeroglíficos. El símbolo de cinco era la letra griega Π (pi), que es la letra de la palabra griega para cinco, pente. Los números del seis al nueve estaban pente con líneas verticales al lado. Diez estaba representado por la letra (Δ) de la palabra diez, deka, cien por la letra de la palabra cien, etc.

La numeración jónica utilizó todo su alfabeto, incluidas tres letras arcaicas. La notación numérica de los griegos, aunque mucho menos conveniente que la que se usa ahora, estaba formada sobre un plan perfectamente regular y científico, y podía usarse con un efecto tolerable como instrumento de cálculo, para cuyo propósito el sistema romano era totalmente inaplicable. Los griegos dividieron las veinticuatro letras de su alfabeto en tres clases y, al agregar otro símbolo a cada clase, tenían caracteres para representar las unidades, las decenas y las centenas. (Astronomie Ancienne de Jean Baptiste Joseph Delambre, t. ii.)

Este sistema apareció en el siglo III a. C., antes de que las letras digamma (Ϝ), koppa (Ϟ) y sampi (Ϡ) quedaran obsoletas. Cuando las letras minúsculas se diferenciaron de las letras mayúsculas, las letras minúsculas se utilizaron como símbolos para la notación. Los múltiplos de mil se escribieron como los nueve números con un trazo delante de ellos: así mil era ",α", dos mil era ",β", etc. M (para μὐριοι, como en "miríada") era se utiliza para multiplicar números por diez mil. Por ejemplo, el número 88.888.888 se escribiría como M,ηωπη*ηωπη

El razonamiento matemático griego era casi completamente geométrico (aunque a menudo se usaba para razonar sobre temas no geométricos como la teoría de números) y, por lo tanto, los griegos no tenían interés en los símbolos algebraicos. La gran excepción fue Diofanto de Alejandría, el gran algebrista. Su Arithmetica fue uno de los textos que utilizó símbolos en las ecuaciones. No era completamente simbólico, pero lo era mucho más que los libros anteriores. Un número desconocido fue llamado s. El cuadrado de s era ; el cubo era ; el cuarto poder era ; y la quinta potencia era .

Notación matemática china

Los chinos usaban números que se parecían mucho al sistema de conteo. Los números del uno al cuatro eran líneas horizontales. Cinco era una X entre dos líneas horizontales; se veía casi exactamente igual que el número romano para diez. Hoy en día, el sistema huāmǎ solo se usa para mostrar precios en los mercados chinos o en facturas escritas a mano tradicionales.

En la historia de los chinos, hubo quienes estaban familiarizados con las ciencias de la aritmética, la geometría, la mecánica, la óptica, la navegación y la astronomía. Las matemáticas en China surgieron de forma independiente en el siglo XI a. Es casi seguro que los chinos estaban familiarizados con varios implementos geométricos o más bien arquitectónicos; con máquinas mecánicas;que conocían la propiedad característica de la aguja magnética; y sabían que los eventos astronómicos ocurrían en ciclos. Los chinos de esa época habían intentado clasificar o ampliar las reglas de la aritmética o la geometría que conocían y explicar las causas de los fenómenos que conocían de antemano. Los chinos desarrollaron de forma independiente números muy grandes y negativos, decimales, un sistema decimal de valor posicional, un sistema binario, álgebra, geometría y trigonometría.

Las matemáticas chinas hicieron contribuciones tempranas, incluido un sistema de valor posicional. El teorema geométrico conocido por los antiguos chinos era aplicable en ciertos casos (a saber, la relación de los lados).Es que también conocían los teoremas geométricos que pueden ser demostrados en la forma cuasi-experimental de la superposición. En aritmética, su conocimiento parece haberse limitado al arte del cálculo por medio del cisne y al poder de expresar los resultados por escrito. Nuestro conocimiento de los primeros logros de los chinos, aunque escaso, es más completo que en el caso de la mayoría de sus contemporáneos. Por lo tanto, es instructivo y sirve para ilustrar el hecho de que se puede saber que una nación puede poseer una habilidad considerable en las artes aplicadas, pero nuestro conocimiento de las matemáticas posteriores en las que se basan esas artes puede ser escaso. El conocimiento de las matemáticas chinas antes del 254 a. C. es algo fragmentario, e incluso después de esta fecha, las tradiciones manuscritas son oscuras.

Como en otras sociedades tempranas, el foco estaba en la astronomía para perfeccionar el calendario agrícola y otras tareas prácticas, y no en establecer sistemas formales. Los deberes de la Junta China de Matemáticas se limitaban a la preparación anual de un almanaque, las fechas y predicciones en las que se regulaba. Los antiguos matemáticos chinos no desarrollaron un enfoque axiomático, pero lograron avances en el desarrollo de algoritmos y álgebra. El logro del álgebra china alcanzó su cenit en el siglo XIII, cuando Zhu Shijie inventó el método de las cuatro incógnitas.

Como resultado de obvias barreras lingüísticas y geográficas, así como de contenido, se presume que las matemáticas chinas y las matemáticas del antiguo mundo mediterráneo se desarrollaron de manera más o menos independiente hasta el momento en que Los nueve capítulos sobre el arte matemático alcanzaron su punto máximo. forma final, mientras que los Escritos sobre el ajuste de cuentas y Huainanzison más o menos contemporáneas con las matemáticas griegas clásicas. Es probable que se produzca algún intercambio de ideas en toda Asia a través de intercambios culturales conocidos desde al menos la época romana. Con frecuencia, elementos de las matemáticas de las sociedades primitivas corresponden a resultados rudimentarios encontrados más tarde en ramas de las matemáticas modernas como la geometría o la teoría de números. El teorema de Pitágoras, por ejemplo, ha sido atestiguado en la época del duque de Zhou. También se ha demostrado que el conocimiento del triángulo de Pascal existió en China siglos antes de Pascal, como por Shen Kuo.

El estado de la trigonometría en China comenzó a cambiar y avanzar lentamente durante la dinastía Song (960-1279), cuando los matemáticos chinos comenzaron a enfatizar más la necesidad de la trigonometría esférica en la ciencia calendárica y los cálculos astronómicos. El erudito científico, matemático y funcionario chino Shen Kuo (1031-1095) utilizó funciones trigonométricas para resolver problemas matemáticos de cuerdas y arcos. Sal Restivo escribe que el trabajo de Shen sobre las longitudes de los arcos de círculos proporcionó la base para la trigonometría esférica desarrollada en el siglo XIII por el matemático y astrónomo Guo Shoujing (1231-1316). Como afirman los historiadores L. Gauchet y Joseph Needham, Guo Shoujing utilizó la trigonometría esférica en sus cálculos para mejorar el sistema calendárico y la astronomía china.La ciencia matemática de los chinos incorporaría el trabajo y la enseñanza de los misioneros árabes con conocimientos de trigonometría esférica que habían llegado a China en el transcurso del siglo XIII.

Numeración y notación india y arábiga

Aunque el origen de nuestro actual sistema de notación numérica es antiguo, no hay duda de que estuvo en uso entre los hindúes hace más de dos mil años. La notación algebraica del matemático indio Brahmagupta era sincopada. La suma se indicaba colocando los números uno al lado del otro, la resta colocando un punto sobre el sustraendo (el número a restar) y la división colocando el divisor debajo del dividendo, similar a nuestra notación pero sin la barra. La multiplicación, la evolución y las cantidades desconocidas se representaron mediante abreviaturas de términos apropiados. El sistema de numeración hindú-árabe y las reglas para el uso de sus operaciones, en uso en todo el mundo hoy en día, probablemente evolucionaron a lo largo del primer milenio dC en la India y se transmitieron a Occidente a través de las matemáticas islámicas.

A pesar de su nombre, los números arábigos tienen raíces en la India. La razón de este nombre inapropiado es que los europeos vieron los números utilizados en un libro árabe, Concerning the Hindu Art of Reckoning, de Mohommed ibn-Musa al-Khwarizmi. Al-Khwārizmī escribió varios libros importantes sobre los números arábigos hindúes y sobre métodos para resolver ecuaciones. Su libro Sobre el cálculo con números hindúes, escrito alrededor de 825, junto con el trabajo de Al-Kindi, fueron fundamentales para difundir las matemáticas indias y los números indios en Occidente. Al-Khwarizmi no reclamó los números como árabes, pero a través de varias traducciones al latín, se perdió el hecho de que los números eran de origen indio. La palabra algoritmo se deriva de la latinización del nombre de Al-Khwārizmī, Algoritmi, y la palabraálgebra del título de una de sus obras, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa'l-muqābala (El libro compendio sobre el cálculo por finalización y equilibrio).

Las matemáticas islámicas desarrollaron y ampliaron las matemáticas conocidas por las civilizaciones de Asia Central. Al-Khwārizmī dio una explicación exhaustiva de la solución algebraica de ecuaciones cuadráticas con raíces positivas, y Al-Khwārizmī enseñaría álgebra en forma elemental y por sí misma. Al-Khwārizmī también discutió el método fundamental de "reducción" y "equilibrio", refiriéndose a la transposición de términos restados al otro lado de una ecuación, es decir, la cancelación de términos similares en lados opuestos de la ecuación. Esta es la operación que al-Khwārizmī describió originalmente como al-jabr.Su álgebra ya no se ocupaba "de una serie de problemas a resolver, sino de una exposición que parte de términos primitivos en los que las combinaciones deben dar todos los prototipos posibles de ecuaciones, que en adelante constituyen explícitamente el verdadero objeto de estudio". Al-Khwārizmī también estudió una ecuación por sí misma y "de manera genérica, en la medida en que no surge simplemente en el curso de la resolución de un problema, sino que está específicamente llamada a definir una clase infinita de problemas".

Al-Karaji, en su tratado al-Fakhri, amplía la metodología para incorporar potencias enteras y raíces enteras de cantidades desconocidas. El historiador de las matemáticas, F. Woepcke, elogió a Al-Karaji por ser "el primero que introdujo la teoría del cálculo algebraico". También en el siglo X, Abul Wafa tradujo las obras de Diofanto al árabe. Ibn al-Haytham desarrollaría la geometría analítica. Al-Haytham derivó la fórmula para la suma de las cuartas potencias, usando un método que es fácilmente generalizable para determinar la fórmula general para la suma de las potencias integrales. Al-Haytham realizó una integración para encontrar el volumen de un paraboloide y pudo generalizar su resultado para las integrales de polinomios hasta el cuarto grado.A fines del siglo XI, Omar Khayyam desarrollaría la geometría algebraica, escribió Discusiones sobre las dificultades en Euclides y escribió sobre la solución geométrica general de las ecuaciones cúbicas. Nasir al-Din Tusi (Nasireddin) hizo avances en trigonometría esférica. Los matemáticos musulmanes durante este período incluyen la adición de la notación del punto decimal a los números arábigos.

Los símbolos numéricos arábigos modernos utilizados en todo el mundo aparecieron por primera vez en el norte de África islámico en el siglo X. Una variante árabe occidental distintiva de los números arábigos orientales comenzó a surgir alrededor del siglo X en el Magreb y Al-Andalus (a veces llamados números ghubar, aunque el término no siempre se acepta), que son el antepasado directo de los números arábigos modernos utilizados alrededor del mundo.

Muchos textos griegos y árabes sobre matemáticas se tradujeron luego al latín, lo que condujo a un mayor desarrollo de las matemáticas en la Europa medieval. En el siglo XII, los eruditos viajaron a España y Sicilia en busca de textos árabes científicos, incluido el de al-Khwārizmī y el texto completo de los Elementos de Euclides. Uno de los libros europeos que abogó por el uso de los numerales fue el Liber Abaci, de Leonardo de Pisa, más conocido como Fibonacci. Liber Abaci es mejor conocido por el problema matemático que Fibonacci escribió sobre una población de conejos. El crecimiento de la población terminó siendo una sucesión de Fibonacci, donde un término es la suma de los dos términos anteriores.

Etapa simbólica

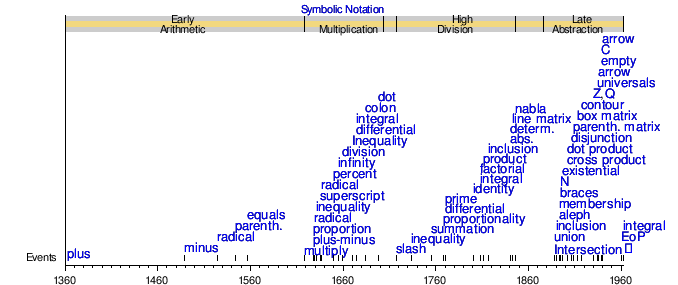
Símbolos por fecha de introducción popular

Aritmética temprana y multiplicación

La transición al álgebra simbólica, donde solo se usan símbolos, se puede ver por primera vez en el trabajo de Ibn al-Banna 'al-Marrakushi (1256–1321) y Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1482). Al-Qalasādī fue el último gran algebrista árabe medieval, que mejoró la notación algebraica utilizada anteriormente en el Magreb por Ibn al-Banna. En contraste con las notaciones sincopadas de sus predecesores, Diofanto y Brahmagupta, que carecían de símbolos para las operaciones matemáticas, la notación algebraica de al-Qalasadi fue la primera en tener símbolos para estas funciones y, por lo tanto, fue "los primeros pasos hacia la introducción del simbolismo algebraico". Representó símbolos matemáticos utilizando caracteres del alfabeto árabe.

El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Los dos símbolos aritméticos más utilizados son la suma y la resta, + y −. El signo más fue utilizado hacia 1360 por Nicole Oresme en su obra Algorismus proporcioneum. Se cree que es una abreviatura de "et", que significa "y" en latín, de la misma manera que el signo ampersand también comenzó como "et". Oresme de la Universidad de París y el italiano Giovanni di Casali proporcionaron de forma independiente demostraciones gráficas de la distancia recorrida por un cuerpo en movimiento uniformemente acelerado, afirmando que el área debajo de la línea representaba la aceleración constante y representaba la distancia total recorrida. El signo menos fue utilizado en 1489 por Johannes Widmann enAritmética mercantil o Behende und hüpsche Rechenung auff allen Kauffmanschafft,. Widmann usó el símbolo menos con el símbolo más para indicar déficit y superávit, respectivamente. En Summa de arithmetica, geometria,proporcioni e proporcionalità, Luca Pacioli usó símbolos para los símbolos más y menos y contenía álgebra.

En el siglo XV, Ghiyath al-Kashi calculó el valor de π al decimosexto lugar decimal. Kashi también tenía un algoritmo para calcular raíces enésimas. En 1533, se publicó la tabla de senos y cosenos de Regiomontanus. Scipione del Ferro y Niccolò Fontana Tartaglia descubrieron soluciones para ecuaciones cúbicas. Gerolamo Cardano las publicó en su libro Ars Magna de 1545, junto con una solución para las ecuaciones de cuarto grado, descubierta por su alumno Lodovico Ferrari. El símbolo radical de la raíz cuadrada fue introducido por Christoph Rudolff. La importante obra de Michael Stifel Arithmetica integracontenía importantes innovaciones en la notación matemática. En 1556, Niccolò Tartaglia usó paréntesis para la agrupación de precedencia. En 1557, Robert Recorde publicó The Whetstone of Witte, que introdujo el signo igual (=), así como los signos más y menos para el lector inglés. En 1564, Gerolamo Cardano analizó los juegos de azar iniciando las primeras etapas de la teoría de la probabilidad. En 1572 Rafael Bombelli publicó su L'Algebra en el que mostraba cómo tratar las cantidades imaginarias que podían aparecer en la fórmula de Cardano para resolver ecuaciones cúbicas. El libro de Simon Stevin De Thiende('el arte de las décimas'), publicado en holandés en 1585, contenía un tratamiento sistemático de la notación decimal, que influyó en todos los trabajos posteriores sobre el sistema de números reales. El Álgebra nueva (1591) de François Viète introdujo la manipulación notacional moderna de las expresiones algebraicas. Para la navegación y mapas precisos de grandes áreas, la trigonometría se convirtió en una rama importante de las matemáticas. Bartholomaeus Pitiscus acuñó la palabra "trigonometría", publicando su Trigonometria en 1595.

John Napier es mejor conocido como el inventor de los logaritmos e hizo común el uso del punto decimal en aritmética y matemáticas. Después de Napier, Edmund Gunter creó las escalas logarítmicas (líneas o reglas) en las que se basan las reglas de cálculo. Fue William Oughtred quien usó dos de esas escalas deslizándose una junto a la otra para realizar multiplicaciones y divisiones directas; y se le acredita como el inventor de la regla de cálculo en 1622. En 1631, Oughtred introdujo el signo de multiplicación (×), su signo de proporcionalidad, y las abreviaturas sen y cos para las funciones seno y coseno. Albert Girard también usó las abreviaturas 'sin', 'cos' y 'tan' para las funciones trigonométricas en su tratado.

Johannes Kepler fue uno de los pioneros de las aplicaciones matemáticas de los infinitesimales. A René Descartes se le acredita como el padre de la geometría analítica, el puente entre el álgebra y la geometría, crucial para el descubrimiento del cálculo y el análisis infinitesimal. En el siglo XVII, Descartes introdujo las coordenadas cartesianas que permitieron el desarrollo de la geometría analítica. Blaise Pascal influyó en las matemáticas a lo largo de su vida. Su Traité du Triangle arithmétique ("Tratado sobre el triángulo aritmético") de 1653 describió una presentación tabular conveniente para los coeficientes binomiales. Pierre de Fermat y Blaise Pascal investigarían la probabilidad. John Wallis introdujo el símbolo del infinito.De manera similar, usó esta notación para infinitesimales. En 1657, Christiaan Huygens publicó el tratado de probabilidad, Sobre el razonamiento en los juegos de azar.

Johann Rahn introdujo el signo de división (÷, una variante de obelus reutilizada) y el signo por lo tanto en 1659. William Jones usó π en Synopsis palmariorum mathesios en 1706 porque es la letra inicial de la palabra griega perimetron (περιμετρον), que significa perímetro en Griego. Este uso fue popularizado en 1737 por Euler. En 1734, Pierre Bouguer usó una doble barra horizontal debajo del signo de desigualdad.

Notación de derivadas: Leibniz y Newton

notaciones derivadas
Señor isaac newton Gottfried Wilhelm Leibniz

El estudio del álgebra lineal surgió del estudio de los determinantes, que se usaban para resolver sistemas de ecuaciones lineales. El cálculo tenía dos sistemas principales de notación, cada uno creado por uno de los creadores: el desarrollado por Isaac Newton y la notación desarrollada por Gottfried Leibniz. La notación de Leibniz es la notación más utilizada hoy en día. El de Newton era simplemente un punto o una raya colocado encima de la función. En el uso moderno, esta notación generalmente denota derivadas de cantidades físicas con respecto al tiempo y se usa con frecuencia en la ciencia de la mecánica. Leibniz, por su parte, utilizó la letra d como prefijo para indicar diferenciación e introdujo la notación que representa las derivadas como si fueran un tipo especial de fracción.Esta notación hace explícita la variable con respecto a la cual se toma la derivada de la función. Leibniz también creó el símbolo integral. El símbolo es una S alargada, que representa la palabra latina Summa, que significa "suma". Al encontrar áreas bajo curvas, la integración a menudo se ilustra dividiendo el área en infinitos rectángulos altos y delgados, cuyas áreas se suman. Así, el símbolo integral es una s alargada, por suma.

Operadores y funciones de alta división

Las letras del alfabeto en este tiempo debían usarse como símbolos de cantidad; y aunque existió mucha diversidad con respecto a la elección de letras, habría varias reglas universalmente reconocidas en la historia siguiente. Aquí, pues, en la historia de las ecuaciones, las primeras letras del alfabeto se conocían indicativamente como coeficientes, las últimas letras como términos desconocidos (an incerti ordinis). En geometría algebraica, de nuevo, se debía observar una regla similar, las últimas letras del alfabeto denotaban allí las coordenadas variables o actuales. Ciertas letras, como , , etc., fueron apropiadas por consentimiento universal como símbolos de los números frecuentes 3.14159... y 2.7182818....,etc., y su uso en cualquier otra aceptación debía evitarse tanto como fuera posible. También debían emplearse letras como símbolos de operación, y con ellas otros caracteres de operación arbitraria mencionados anteriormente. Las letras , alargadas debían ser apropiadas como símbolos operativos en el cálculo diferencial y el cálculo integral, y Σ en el cálculo de diferencias. En notación funcional, una letra, como símbolo de operación, se combina con otra que se considera como símbolo de cantidad.

A partir de 1718, Thomas Twinin utilizó la barra de división (solidus), derivándola de la anterior barra de fracción horizontal árabe. Pierre-Simon, marqués de Laplace, desarrolló el ampliamente utilizado operador diferencial laplaciano. En 1750, Gabriel Cramer desarrolló la "Regla de Cramer " para resolver sistemas lineales.

Notaciones de Euler y prima

Leonhard Euler fue uno de los matemáticos más prolíficos de la historia y también un prolífico inventor de la notación canónica. Sus contribuciones incluyen el uso de e para representar la base de los logaritmos naturales. No se sabe exactamente por qué se eligió, pero probablemente fue porque las cuatro letras del alfabeto ya se usaban comúnmente para representar variables y otras constantes. Euler solía representar pi consistentemente. El uso de fue sugerido por William Jones, quien lo utilizó como abreviatura de perímetro. Euler solía representar la raíz cuadrada de menos uno, aunque antes lo usaba como un número infinito. Para la suma, Euler usó sigma, Σ. Para funciones, Euler usó la notaciónpara representar una función de . En 1730, Euler escribió la función gamma. En 1736, Euler produce su artículo sobre los Siete Puentes de Königsberg iniciando el estudio de la teoría de grafos.

El matemático William Emerson desarrollaría el signo de proporcionalidad. Mucho más tarde, en las expresiones abstractas del valor de varios fenómenos proporcionales, la notación de partes por se volvería útil como un conjunto de pseudounidades para describir pequeños valores de cantidades adimensionales misceláneas. El marqués de Condorcet, en 1768, avanzó el signo diferencial parcial. En 1771, Alexandre-Théophile Vandermonde dedujo la importancia de las características topológicas al discutir las propiedades de los nudos relacionadas con la geometría de la posición. Entre 1772 y 1788, Joseph-Louis Lagrange reformuló las fórmulas y cálculos de la mecánica clásica "newtoniana", denominada mecánica lagrangiana. Lagrange también hizo el símbolo principal para los derivados.

Pero, en nuestra opinión, las verdades de este tipo deberían extraerse de nociones más que de notaciones.—Carl  Friedrich Gauss

Notaciones de Gauss, Hamilton y Matrix

A principios del siglo XIX, Carl Friedrich Gauss desarrolló el signo de identidad para la relación de congruencia y, en reciprocidad cuadrática, la parte integral. Gauss aportó funciones de variables complejas, en geometría y en la convergencia de series. Dio las demostraciones satisfactorias del teorema fundamental del álgebra y de la ley de reciprocidad cuadrática. Gauss desarrolló la teoría de resolver sistemas lineales mediante la eliminación de Gauss, que inicialmente se catalogó como un avance en la geodesia. También desarrollaría el letrero del producto. También en esta época, Niels Henrik Abel y Évariste Galois realizaron su trabajo sobre la resolución de ecuaciones, vinculando la teoría de grupos y la teoría de campos.

Después de la década de 1800, Christian Kramp promovería la notación factorial durante su investigación sobre la función factorial generalizada que se aplicaba a números no enteros. Joseph Diaz Gergonne introdujo los signos de inclusión de conjuntos. Peter Gustav Lejeune Dirichlet desarrolló las funciones L de Dirichlet para demostrar el teorema de Dirichlet sobre las progresiones aritméticas y comenzó la teoría analítica de números. En 1828, Gauss demostró su Teorema Egregium (teorema notableen latín), estableciendo la propiedad de las superficies. En la década de 1830, George Green desarrolló la función de Green. En 1829, Carl Gustav Jacob Jacobi publica Fundamenta nova theoriae functionum ellipticarum con sus funciones theta elípticas. En 1841, Karl Weierstrass, el "padre del análisis moderno", elaboró ​​​​el concepto de valor absoluto y el determinante de una matriz.

Arthur Cayley desarrollaría más completamente la notación matricial en sus tres artículos, sobre temas que habían sido sugeridos al leer la Mécanique analytique de Lagrange y algunas de las obras de Laplace. Cayley definió la multiplicación de matrices y las inversas de matrices. Cayley usó una sola letra para denotar una matriz, tratando así una matriz como un objeto agregado. También se dio cuenta de la conexión entre matrices y determinantes, y escribió: " Habría muchas cosas que decir sobre esta teoría de matrices que, me parece, debería preceder a la teoría de determinantes ".

[... El cuaternión matemático] tiene, o al menos implica una referencia a, cuatro dimensiones.—William  Rowan Hamilton

William Rowan Hamilton introduciría el símbolo nabla para diferenciales vectoriales. Esto fue utilizado anteriormente por Hamilton como un letrero de operador de uso general. Hamilton reformuló la mecánica newtoniana, ahora llamada mecánica hamiltoniana. Este trabajo ha demostrado ser fundamental para el estudio moderno de las teorías de campo clásicas como el electromagnetismo. Esto también fue importante para el desarrollo de la mecánica cuántica. En matemáticas, es quizás mejor conocido como el inventor de la notación de cuaterniones y bicuaterniones. Hamilton también introdujo la palabra "tensor" en 1846. James Cockle desarrollaría las tessarinas y, en 1849, los cocuaterniones. En 1848, James Joseph Sylvester introdujo en el álgebra matricial el término matriz.

Notaciones de Maxwell, Clifford y Ricci

En 1864, James Clerk Maxwell redujo todo el conocimiento actual sobre electromagnetismo en un conjunto vinculado de ecuaciones diferenciales con 20 ecuaciones en 20 variables, contenidas en A Dynamical Theory of the Electromagnetic Field. (Véanse las ecuaciones de Maxwell.) El método de cálculo que es necesario emplear fue dado por Lagrange, y luego desarrollado, con algunas modificaciones, por las ecuaciones de Hamilton. Por lo general, se lo conoce como el principio de Hamilton; cuando se utilizan las ecuaciones en su forma original, se conocen como ecuaciones de Lagrange. En 1871, Richard Dedekind llamó campo a un conjunto de números reales o complejos cerrados bajo las cuatro operaciones aritméticas. En 1873 Maxwell presentó Tratado sobre electricidad y magnetismo.

En 1878, William Kingdon Clifford publicó su obra Elements of Dynamic. Clifford desarrolló bicuaterniones divididos, a los que llamó motores algebraicos. Clifford obvió el estudio de cuaterniones separando el producto escalar y el producto vectorial de dos vectores de la notación completa de cuaterniones. Este enfoque hizo que el cálculo vectorial estuviera disponible para los ingenieros y otras personas que trabajaban en tres dimensiones y eran escépticos sobre el efecto de adelanto-retraso en la cuarta dimensión. Las notaciones vectoriales comunes se utilizan cuando se trabaja con vectores que son miembros espaciales o más abstractos de espacios vectoriales, mientras que la notación angular (o notación fasorial) es una notación utilizada en electrónica.

En 1881, Leopold Kronecker definió lo que llamó un "dominio de la racionalidad", que es una extensión del campo de los números racionales en términos modernos. En 1882, Hüseyin Tevfik Paşa [ tr ] escribió el libro titulado "Álgebra lineal". La teoría del átomo etérico de Lord Kelvin (década de 1860) llevó a Peter Guthrie Tait, en 1885, a publicar una tabla topológica de nudos con hasta diez cruces conocida como las conjeturas de Tait. En 1893, Heinrich M. Weber dio la clara definición de un campo abstracto. El cálculo tensorial fue desarrollado por Gregorio Ricci-Curbastro entre 1887 y 1896, presentado en 1892 bajo el título de cálculo diferencial absoluto, y el uso contemporáneo de "tensor" fue declarado por Woldemar Voigt en 1898.En 1895, Henri Poincaré publicó Análisis situs. En 1897, Charles Proteus Steinmetz publicaría Teoría y cálculo de fenómenos de corriente alterna, con la ayuda de Ernst J. Berg.

De las fórmulas matemáticas a los tensores

La proposición anterior es ocasionalmente útil.—Bertrand  Russell

En 1895, Giuseppe Peano publicó su Formulario matemático, un esfuerzo por digerir las matemáticas en un texto conciso basado en símbolos especiales. Proporcionaría una definición de un espacio vectorial y un mapa lineal. También introduciría el signo de intersección, el signo de unión, el signo de membresía (es un elemento de) y el cuantificador existencial (existe). Peano pasaría a Bertrand Russell su trabajo en 1900 en una conferencia en París; impresionó tanto a Russell que Russell también se sintió atraído por el impulso de hacer las matemáticas de manera más concisa. El resultado fue Principia Mathematica escrito con Alfred North Whitehead. Este tratado marca un hito en la literatura moderna donde el símbolo se volvió dominante. Ricci-Curbastro y Tullio Levi-Civita popularizaron la notación del índice tensorial alrededor de 1900.

Lógica matemática y abstracción

Abstracción
Félix Klein Jorge Cantor

Al comienzo de este período, el "programa Erlangen" de Felix Klein identificó el tema subyacente de varias geometrías, definiendo cada una de ellas como el estudio de propiedades invariantes bajo un grupo dado de simetrías. Este nivel de abstracción reveló conexiones entre la geometría y el álgebra abstracta. Georg Cantor introduciría el símbolo aleph para los números cardinales de conjuntos transfinitos. Su notación para los números cardinales era la letra hebrea(aleph) con subíndice de número natural; para los ordinales empleó la letra griega ω (omega). Esta notación todavía se usa hoy en día en la notación ordinal de una secuencia finita de símbolos de un alfabeto finito que nombra un número ordinal de acuerdo con algún esquema que le da significado al lenguaje. Su teoría generó una gran controversia. Cantor, en su estudio de las series de Fourier, consideraría conjuntos de puntos en el espacio euclidiano.

Después de la vuelta del siglo XX, Josiah Willard Gibbs introduciría en la química física el punto medio para el producto punto y el signo de multiplicación para los productos cruzados. También proporcionaría notación para los productos escalares y vectoriales, que se introdujo en Vector Analysis. En 1904, Ernst Zermelo promueve el axioma de elección y su demostración del teorema del buen orden. Bertrand Russell introduciría poco después la disyunción lógica (OR) en 1906. También en 1906, Poincaré publicaría Sobre la dinámica del electrón y Maurice Fréchet introdujo el espacio métrico. Más tarde, Gerhard Kowalewski y Cuthbert Edmund Cullis introducirían sucesivamente la notación de matrices, la matriz entre paréntesis y la notación de matriz de caja, respectivamente. Después de 1907, los matemáticosestudió los nudos desde el punto de vista del grupo de nudos y las invariantes desde la teoría de la homología. En 1908, se formularon los teoremas de estructura de Joseph Wedderburn para álgebras de dimensión finita sobre un campo. También en 1908, Ernst Zermelo propuso la propiedad "definida" y la primera teoría axiomática de conjuntos, la teoría de conjuntos de Zermelo. En 1910, Ernst Steinitz publicó el influyente artículo Teoría algebraica de campos. En 1911, Steinmetz publicaría Teoría y cálculo de fenómenos eléctricos transitorios y oscilaciones.

Albert Einstein, en 1916, introdujo la notación de Einstein que sumaba un conjunto de términos indexados en una fórmula, ejerciendo así brevedad notacional. Arnold Sommerfeld crearía el signo integral de contorno en 1917. También en 1917, Dimitry Mirimanoff propone el axioma de regularidad. En 1919, Theodor Kaluza resolvería las ecuaciones de la relatividad general usando cinco dimensiones, los resultados harían emerger las ecuaciones electromagnéticas. Esto sería publicado en 1921 en "Zum Unitätsproblem der Physik". En 1922, Abraham Fraenkel y Thoralf Skolem propusieron de forma independiente reemplazar el esquema de axioma de especificación con el esquema de axioma de reemplazo. También en 1922, se desarrolló la teoría de conjuntos de Zermelo-Fraenkel. En 1923, Steinmetz publicaría Four Lectures on Relativity and Space. Alrededor de 1924, Jan Arnoldus Schouten desarrollaría la notación y el formalismo modernos para el marco de cálculo de Ricci durante las aplicaciones del cálculo diferencial absoluto a la relatividad general y la geometría diferencial a principios del siglo XX. En 1925, Enrico Fermi describiría un sistema formado por muchas partículas idénticas que obedecen al principio de exclusión de Pauli, desarrollando posteriormente una ecuación de difusión (ecuación de edad de Fermi). En 1926, Oskar Klein desarrollaría la teoría de Kaluza-Klein. En 1928, Emil Artin abstrajo la teoría de los anillos con los anillos artinianos. En 1933, Andrey Kolmogorov introduce los axiomas de Kolmogorov. En 1937, Bruno de Finetti dedujo el concepto de "subjetivo operacional".

Simbolismo matematico

La abstracción matemática comenzó como un proceso de extracción de la esencia subyacente de un concepto matemático, eliminando cualquier dependencia de los objetos del mundo real con los que originalmente podría haber estado conectado y generalizándolo para que tenga aplicaciones más amplias o coincida con otras descripciones abstractas de fenómenos equivalentes.. Dos áreas abstractas de las matemáticas modernas son la teoría de categorías y la teoría de modelos. Bertrand Russell, dijo: " El lenguaje ordinario es totalmente inadecuado para expresar lo que la física realmente afirma, ya que las palabras de la vida cotidiana no son lo suficientemente abstractas. Solo las matemáticas y la lógica matemática pueden decir tan poco como el físico quiere decir ".". Sin embargo, uno puede sustituir las matemáticas por objetos del mundo real, y deambular ecuación tras ecuación, y puede construir una estructura conceptual que no tiene relación con la realidad.

La lógica simbólica estudia las propiedades puramente formales de cadenas de símbolos. El interés en esta área surge de dos fuentes. En primer lugar, se puede considerar que la notación utilizada en la lógica simbólica representa las palabras utilizadas en la lógica filosófica. En segundo lugar, las reglas para manipular símbolos que se encuentran en la lógica simbólica se pueden implementar en una máquina de cómputo. La lógica simbólica se suele dividir en dos subcampos, la lógica proposicional y la lógica de predicados. Otras lógicas de interés incluyen la lógica temporal, la lógica modal y la lógica difusa. El área de la lógica simbólica llamada lógica proposicional, también llamada cálculo proposicional., estudia las propiedades de las oraciones formadas a partir de constantes y operadores lógicos. Las operaciones lógicas correspondientes se conocen, respectivamente, como conjunción, disyunción, condicional material, bicondicional y negación. Estos operadores se denotan como palabras clave y mediante notación simbólica.

Parte de la notación lógica matemática introducida durante este tiempo incluía el conjunto de símbolos utilizados en el álgebra booleana. Este fue creado por George Boole en 1854. El propio Boole no veía la lógica como una rama de las matemáticas, pero de todos modos se ha llegado a abarcar. Los símbolos que se encuentran en el álgebra booleana incluyen (Y), (O) y (no). Con estos símbolos y letras para representar diferentes valores de verdad, uno puede hacer afirmaciones lógicas como , es decir, "(a es verdadero O a no es verdadero) es verdadero", lo que significa que es verdadero que unes verdadero o no verdadero (es decir, falso). El álgebra de Boole tiene muchos usos prácticos, pero también fue el comienzo de lo que sería un gran conjunto de símbolos para usar en lógica. La lógica de predicados, originalmente llamada cálculo de predicados, amplía la lógica proposicional mediante la introducción de variables y oraciones que contienen variables, llamadas predicados. Además, la lógica de predicados permite cuantificadores. Con estos símbolos lógicos y cuantificadores adicionales de la lógica de predicados, se pueden hacer pruebas válidas que son irracionalmente artificiales, pero sintácticas.

Notación de incompletitud de Gödel

A cada clase recursiva κ consistente con ω de fórmulas le corresponden signos de clase recursiva r, tales que ni v Gen r ni Neg (v Gen r) pertenecen a Flg (κ) (donde v es la variable libre de r).—  Kurt Godel

Mientras demostraba sus teoremas de incompletitud, Kurt Gödel creó una alternativa a los símbolos normalmente utilizados en lógica. Usó números de Gödel, que eran números que representaban operaciones con números fijos y variables con números primos mayores que 10. Con los números de Gödel, las declaraciones lógicas se pueden dividir en una secuencia numérica. Gödel luego llevó esto un paso más allá, tomando los n números primos y elevándolos a la potencia de los números en la secuencia. Luego, estos números se multiplicaron para obtener el producto final, dando a cada declaración lógica su propio número.

Notación y temas contemporáneos

Notación de principios del siglo XX

La abstracción de la notación es un proceso continuo y el desarrollo histórico de muchos temas matemáticos exhibe una progresión de lo concreto a lo abstracto. Se desarrollarían varias notaciones de conjuntos para conjuntos de objetos fundamentales. Alrededor de 1924, David Hilbert y Richard Courant publicaron "Métodos de física matemática. Ecuaciones diferenciales parciales". En 1926, Oskar Klein y Walter Gordon propusieron la ecuación de Klein-Gordon para describir partículas relativistas. La primera formulación de una teoría cuántica que describe la interacción entre la radiación y la materia se debe a Paul Adrien Maurice Dirac, quien, durante 1920, fue capaz de calcular por primera vez el coeficiente de emisión espontánea de un átomo.En 1928, Dirac formuló la ecuación relativista de Dirac para explicar el comportamiento del electrón en movimiento relativista. Dirac describió la cuantificación del campo electromagnético como un conjunto de osciladores armónicos con la introducción del concepto de operadores de creación y aniquilación de partículas. En los años siguientes, con las contribuciones de Wolfgang Pauli, Eugene Wigner, Pascual Jordan y Werner Heisenberg, y una elegante formulación de la electrodinámica cuántica de Enrico Fermi, los físicos llegaron a creer que, en principio, sería posible realizar cualquier cálculo. para cualquier proceso físico que involucre fotones y partículas cargadas.

En 1931, Alexandru Proca desarrolló la ecuación de Proca (ecuación de Euler-Lagrange) para la teoría del mesón vectorial de las fuerzas nucleares y las ecuaciones de campo cuánticas relativistas. John Archibald Wheeler en 1937 desarrolla S-matrix. Los estudios de Felix Bloch con Arnold Nordsieck y Victor Weisskopf, en 1937 y 1939, revelaron que tales cálculos eran confiables solo en un primer orden de la teoría de la perturbación, un problema ya señalado por Robert Oppenheimer. En los órdenes superiores de la serie surgieron infinitos, lo que hizo que tales cálculos no tuvieran sentido y arrojó serias dudas sobre la consistencia interna de la teoría misma. Sin una solución conocida para este problema en ese momento, parecía que existía una incompatibilidad fundamental entre la relatividad especial y la mecánica cuántica.

En la década de 1930, Edmund Landau creó la Z mayúscula de dos puntas para conjuntos de números enteros. Nicolas Bourbaki creó la Q mayúscula doble para conjuntos de números racionales. En 1935, Gerhard Gentzen hizo cuantificadores universales. En 1936, Alfred Tarski establece y prueba el teorema de indefinibilidad de Tarski. En 1938, Gödel propone el universo construible en el artículo " La consistencia del axioma de elección y de la hipótesis-continua generalizada ". André Weil y Nicolas Bourbaki desarrollarían el signo de conjunto vacío en 1939. Ese mismo año, Nathan Jacobson acuñaría la C mayúscula de doble acuñación para conjuntos de números complejos.

Alrededor de la década de 1930, la notación de Voigt se desarrollaría para el álgebra multilineal como una forma de representar un tensor simétrico mediante la reducción de su orden. La notación de Schönflies se convirtió en una de las dos convenciones utilizadas para describir grupos de puntos (la otra es la notación de Hermann-Mauguin). También en esta época, la notación de van der Waerden se hizo popular por el uso de espinores de dos componentes (espinores de Weyl) en cuatro dimensiones del espacio-tiempo. Arend Heyting introduciría el álgebra de Heyting y la aritmética de Heyting.

La flecha, por ejemplo, →, fue desarrollada para la notación de funciones en 1936 por Øystein Ore para denotar imágenes de elementos específicos. Más tarde, en 1940, tomó su forma actual, por ejemplo, f: X → Y, gracias al trabajo de Witold Hurewicz. Werner Heisenberg, en 1941, propuso la teoría de la matriz S de las interacciones de partículas.

La notación de corchetes (notación de Dirac) es una notación estándar para describir estados cuánticos, compuesta por corchetes angulares y barras verticales. También se puede utilizar para denotar vectores abstractos y funcionales lineales. Se llama así porque el producto interno (o producto escalar en un espacio vectorial complejo) de dos estados se denota por un ⟨bra|ket⟩ que consta de una parte izquierda, ⟨ φ |, y una parte derecha, | ψ⟩. La notación fue introducida en 1939 por Paul Dirac, aunque la notación tiene precursores en el uso de Grassmann de la notación [ φ | ψ ] por sus productos internos casi 100 años antes.

La notación bra-ket está muy extendida en la mecánica cuántica: casi todos los fenómenos que se explican mediante la mecánica cuántica, incluida una gran parte de la física moderna, generalmente se explican con la ayuda de la notación bra-ket. La notación establece una representación-independencia abstracta codificada, produciendo una representación específica versátil (p. ej., x, o p, o base de función propia) sin mucha dificultad o dependencia excesiva de la naturaleza de los espacios lineales involucrados. La expresión de superposición ⟨ φ | ψ ⟩ generalmente se interpreta como la amplitud de probabilidad para que el estado ψ colapse en el estado ϕ. La notación de barra de Feynman (notación de barra de Dirac) fue desarrollado por Richard Feynman para el estudio de los campos de Dirac en la teoría cuántica de campos.

En 1948, Valentine Bargmann y Eugene Wigner propusieron las ecuaciones relativistas de Bargmann-Wigner para describir partículas libres y las ecuaciones tienen la forma de funciones de onda de campo de espinor de componentes múltiples. En 1950, William Vallance Douglas Hodge presentó "Las invariantes topológicas de las variedades algebraicas" en las Actas del Congreso Internacional de Matemáticos. Entre 1954 y 1957, Eugenio Calabi trabajó en la conjetura de Calabi para la métrica de Kähler y el desarrollo de las variedades de Calabi-Yau. En 1957, Tullio Regge formuló la propiedad matemática de la dispersión potencial en la ecuación de Schrödinger.Stanley Mandelstam, junto con Regge, hizo el desarrollo inicial de la teoría Regge de fenomenología de interacción fuerte. En 1958, Murray Gell-Mann y Richard Feynman, junto con George Sudarshan y Robert Marshak, dedujeron las estructuras quirales de la interacción débil en física. Geoffrey Chew, junto con otros, promovería la notación matricial para la interacción fuerte y el principio de arranque asociado en 1960. En la década de 1960, se desarrolló la notación de creación de conjuntos para describir un conjunto al establecer las propiedades que sus miembros deben satisfacer. También en la década de 1960, los tensores se abstraen dentro de la teoría de categorías mediante el concepto de categoría monoide. Posteriormente, la notación multiíndice elimina las nociones convencionales utilizadas en el cálculo multivariable, las ecuaciones diferenciales parciales y la teoría de las distribuciones.

Notación matemática moderna

En las matemáticas modernas de la relatividad especial, el electromagnetismo y la teoría ondulatoria, el operador de d'Alembert es el operador de Laplace del espacio de Minkowski. El símbolo de Levi-Civita se usa en cálculo tensorial.

Después de las formulaciones completas de covarianza de Lorentz que eran finitas en cualquier orden en una serie de perturbaciones de electrodinámica cuántica, Sin-Itiro Tomonaga, Julian Schwinger y Richard Feynman recibieron conjuntamente un premio Nobel de física en 1965.Sus contribuciones, y las de Freeman Dyson, fueron sobre formulaciones covariantes e invariantes de calibre de la electrodinámica cuántica que permiten cálculos de observables en cualquier orden de la teoría de la perturbación. La técnica matemática de Feynman, basada en sus diagramas, inicialmente parecía muy diferente del enfoque de la teoría de campos y basado en operadores de Schwinger y Tomonaga, pero Freeman Dyson demostró más tarde que los dos enfoques eran equivalentes. La renormalización, la necesidad de dar un significado físico a ciertas divergencias que aparecen en la teoría a través de integrales, se ha convertido posteriormente en uno de los aspectos fundamentales de la teoría cuántica de campos y ha llegado a ser visto como un criterio para la aceptabilidad general de una teoría. La electrodinámica cuántica ha servido como modelo y plantilla para posteriores teorías cuánticas de campos. pedro higgs, Jeffrey Goldstone y otros, Sheldon Glashow, Steven Weinberg y Abdus Salam mostraron de forma independiente cómo la fuerza nuclear débil y la electrodinámica cuántica podrían fusionarse en una sola fuerza electrodébil. A fines de la década de 1960, el zoológico de partículas estaba compuesto por las partículas elementales entonces conocidas antes del descubrimiento de los quarks.

Un paso hacia el Modelo Estándar fue el descubrimiento de Sheldon Glashow, en 1960, de una forma de combinar las interacciones electromagnética y débil. En 1967, Steven Weinberg y Abdus Salam incorporaron el mecanismo de Higgs a la teoría electrodébil de Glashow, dándole su forma moderna. Se cree que el mecanismo de Higgs da lugar a las masas de todas las partículas elementales en el modelo estándar. Esto incluye las masas de los bosones W y Z, y las masas de los fermiones, es decir, los quarks y los leptones. También en 1967, Bryce DeWitt publicó su ecuación con el nombre de " Ecuación de Einstein-Schrödinger " (más tarde rebautizada como " Ecuación de Wheeler-DeWitt ").En 1969, Yoichiro Nambu, Holger Bech Nielsen y Leonard Susskind describieron el espacio y el tiempo en términos de cuerdas. En 1970, Pierre Ramond desarrolla supersimetrías bidimensionales. Michio Kaku y Keiji Kikkawa luego formularían variaciones de cuerdas. En 1972, Michael Artin, Alexandre Grothendieck, Jean-Louis Verdier proponen el universo Grothendieck.

Después de las corrientes débiles neutrales causadas porZintercambio de bosones fueron descubiertos en el CERN en 1973,la teoría electrodébil fue ampliamente aceptada y Glashow, Salam y Weinberg compartieron el Premio Nobel de Física de 1979 por descubrirla. La teoría de la interacción fuerte, a la que muchos contribuyeron, adquirió su forma moderna alrededor de 1973-1974. Con el establecimiento de la cromodinámica cuántica, finalizó un conjunto de partículas fundamentales y de intercambio, lo que permitió el establecimiento de un "modelo estándar" basado en las matemáticas de la invariancia de calibre, que describió con éxito todas las fuerzas excepto la gravedad, y que sigue siendo generalmente aceptado. dentro del dominio al que está diseñado para ser aplicado. A fines de la década de 1970, William Thurston introdujo la geometría hiperbólica en el estudio de los nudos con el teorema de hiperbolización. El sistema de notación orbifold, inventado por Thurston, ha sido desarrollado para representar tipos de grupos de simetría en espacios bidimensionales de curvatura constante. En 1978, Shing-Tung Yau dedujo que la conjetura de Calabi tiene métrica plana de Ricci. En 1979, Daniel Friedan demostró que las ecuaciones de movimiento de la teoría de cuerdas son abstracciones de las ecuaciones de Einstein de la Relatividad General.

La primera revolución de supercuerdas se compone de ecuaciones matemáticas desarrolladas entre 1984 y 1986. En 1984, Vaughan Jones dedujo el polinomio de Jones y las contribuciones posteriores de Edward Witten, Maxim Kontsevich y otros, revelaron conexiones profundas entre la teoría de nudos y los métodos matemáticos en mecánica estadística y teoría cuántica de campos. De acuerdo con la teoría de cuerdas, todas las partículas en el "zoológico de partículas" tienen un ancestro común, a saber, una cuerda vibrante. En 1985, Philip Candelas, Gary Horowitz, Andrew Strominger y Edward Witten publicarían "Configuraciones al vacío para supercuerdas".Posteriormente, se introduciría el formalismo de tétrada (notación de índice de tétrada) como un enfoque de la relatividad general que reemplaza la elección de una base de coordenadas por la elección menos restrictiva de una base local para el paquete tangente.

En la década de 1990, Roger Penrose propondría la notación gráfica de Penrose (notación de diagrama de tensores) como una representación visual, generalmente escrita a mano, de funciones multilineales o tensores. Penrose también introduciría la notación de índice abstracto. En 1995, Edward Witten sugirió la teoría M y posteriormente la utilizó para explicar algunas dualidades observadas, iniciando la segunda revolución de las supercuerdas.

John Conway promovería varias notaciones, incluida la notación de flecha encadenada de Conway, la notación de teoría de nudos de Conway y la notación de poliedro de Conway. El sistema de notación de Coxeter clasifica los grupos de simetría, describiendo los ángulos entre los reflejos fundamentales de un grupo de Coxeter. Utiliza una notación entre paréntesis, con modificadores para indicar ciertos subgrupos. La notación lleva el nombre de HSM Coxeter y Norman Johnson la definió de manera más completa.

La notación LCF combinatoria se ha desarrollado para la representación de gráficos cúbicos que son hamiltonianos. La notación de ciclo es la convención para escribir una permutación en términos de sus ciclos constituyentes. Esto también se llama notación circular y la permutación se llama permutación cíclica o circular.

Computadoras y notación de marcado

En 1931, IBM produce el IBM 601 Multiplying Punch; es una máquina electromecánica que podría leer dos números, de hasta 8 dígitos, de una tarjeta y perforar su producto en la misma tarjeta. En 1934, Wallace Eckert usó un IBM 601 Multiplying Punch manipulado para automatizar la integración de ecuaciones diferenciales. En 1936, Alan Turing publica "Sobre números computables, con una aplicación al Entscheidungsproblem". John von Neumann, pionero de la computadora digital y de la informática, en 1945, escribe el incompleto Primer Borrador de un Informe sobre el EDVAC. En 1962, Kenneth E. Iverson desarrolló una notación de parte integral, que se convirtió en APL, para manipular matrices que enseñó a sus alumnos y describió en su libro Un lenguaje de programación.. En 1970, Edgar F. Codd propuso el álgebra relacional como modelo relacional de datos para lenguajes de consulta de bases de datos. En 1971, Stephen Cook publica "La complejidad de los procedimientos de demostración de teoremas".En la década de 1970, dentro de la arquitectura informática, se desarrolló la notación de cotizaciones para representar un sistema numérico de números racionales. También en esta década, la notación Z (al igual que el lenguaje APL, mucho antes) usa muchos símbolos que no son ASCII, la especificación incluye sugerencias para representar los símbolos de notación Z en ASCII y en LaTeX. Actualmente existen varias funciones matemáticas C (Math.h) y bibliotecas numéricas. Son bibliotecas utilizadas en el desarrollo de software para realizar cálculos numéricos. Estos cálculos pueden manejarse mediante ejecuciones simbólicas; analizar un programa para determinar qué entradas hacen que se ejecute cada parte de un programa. Mathematica y SymPy son ejemplos de programas de software computacional basados ​​en matemáticas simbólicas.

Futuro de la notación matemática

En la historia de la notación matemática, la notación de símbolos ideográficos ha cerrado el círculo con el surgimiento de los sistemas de visualización por computadora. Las notaciones se pueden aplicar a visualizaciones abstractas, como para representar algunas proyecciones de una variedad de Calabi-Yau. Ejemplos de visualización abstracta que pertenecen propiamente a la imaginación matemática se pueden encontrar en gráficos por computadora. La necesidad de tales modelos abunda, por ejemplo, cuando las medidas para el tema de estudio son en realidad variables aleatorias y no funciones matemáticas ordinarias.