Grupo cuaternión

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tabla de multiplicación de grupo de cuaternión (forma simplificada)
	$1$	$i$	$j$	$k$
$1$	$1$	$i$	$j$	$k$
$i$	$i$	$-1$	$k$	$- j$
$j$	$j$	$- k$	$-1$	$i$
$k$	$k$	$j$	$- i$	$-1$

Diagrama del ciclo de Q₈. Cada color especifica una serie de poderes de cualquier elemento conectado al elemento de identidad e = 1. Por ejemplo, el ciclo en rojo refleja el hecho de que yo² = e, yo³ = i y yo⁴ = e. El ciclo rojo también refleja que i² = e, i³ = i i⁴ = e.

En la teoría del grupo, quaternion group Q₈ (a veces simplemente denotado por Q) es un grupo no-abeliano de orden ocho, isomorfo al subconjunto de ocho elementos ${displaystyle {1,i,j,k,-1,-i,-j,-k}$ de las quaternions bajo multiplicación. Es dada por la presentación del grupo

{displaystyle mathrm {Q} _{8}=langle {bar {e},i,j,kmid {bar} ## {2}=e,;i^{2}=j^{2}=k^{2}=ijk={bar} {e}rangle}

donde e es el elemento de identidad y e conmuta con los otros elementos del grupo.

Otra presentación de Q8 es

{displaystyle mathrm {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

Comparado con el grupo diédrico

El grupo de cuaterniones Q₈ tiene el mismo orden que el grupo diédrico D4, pero una estructura diferente, como lo muestran sus gráficos de Cayley y de ciclo:

	Q₈	D4
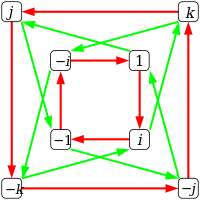
Gráfico de Cayley	Las flechas rojas conectan g→#, conexión verde g→gj.
Gráfico del ciclo

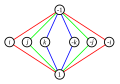En los diagramas para D₄, los elementos del grupo están marcados con su acción en una letra F en la representación definitoria R². No se puede hacer lo mismo con Q₈, ya que no tiene una representación fiel en R² o R³. D₄ se puede realizar como un subconjunto de los cuaterniones divididos de la misma manera que Q₈ se puede ver como un subconjunto de los cuaterniones.

Mesa Cayley

La tabla de Cayley (tabla de multiplicar) para Q₈ viene dada por:

×	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
i	i	i	e	e	k	k	j	j
i	i	i	e	e	k	k	j	j
j	j	j	k	k	e	e	i	i
j	j	j	k	k	e	e	i	i
k	k	k	j	j	i	i	e	e
k	k	k	j	j	i	i	e	e

Propiedades

Los elementos i, j y k tienen orden cuatro en Q₈ y dos cualesquiera de ellos generan todo el grupo. Otra presentación de Q₈ basada en solo dos elementos para evitar esta redundancia es:

{displaystyle leftlangle x,ymid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}rightrangle.}

Uno puede tomar, por ejemplo, ${displaystyle i=x,j=y,}$ y ${displaystyle k=xy}$ .

El grupo cuaternión tiene la propiedad inusual de ser hamiltoniano: Q₈ no es abeliano, pero todos los subgrupos son normales. Cada grupo hamiltoniano contiene una copia de Q₈.

El grupo cuaternión Q₈ y el grupo diédrico D₄ son los dos ejemplos más pequeños de un grupo nilpotente no abeliano.

El centro y el subgrupo de conmutadores de Q₈ es el subgrupo ${displaystyle {e,{bar {}}}}$ . El grupo de automorfismo interno de Q₈ es dado por el grupo modulo su centro, es decir, el grupo factor ${displaystyle mathrm {Q} _{8}/{e,{bar {e}}}}$ que es isomorfo para el grupo V de Klein. El grupo de automorfismo completo de Q₈ es isomorfo a S₄, el grupo simétrico sobre cuatro letras (ver Representaciones de matriz abajo), y el grupo de automorfismo externo de Q₈ por lo tanto S₄/V, que es isomorfo a S₃.

Grupo de cuaternión Q₈ tiene cinco clases de conjugación, ${displaystyle {e}, {fnMicrosoft Sans Serif}\fnMicrosoft Sans Serif} {fnK}\fnMicrosoft Sans Serif}$ y así cinco representaciones irreducibles sobre los números complejos, con dimensiones 1, 1, 1, 2,

Representación trivial.

Representaciones de signos con i, j, k-kernel: Q₈ tiene tres subgrupos normales máximos: los subgrupos cíclicos generados por i, j y k respectivamente. Para cada subgrupo normal máximo N, obtenemos una representación unidimensional factorizando a través del grupo de cociente de 2 elementos G/N. La representación envía elementos de N a 1, y elementos fuera de N a −1.

Representación bidimensional: se describe a continuación en Representaciones matriciales.

La tabla de caracteres de Q₈ resulta ser la misma que la de D₄:

Representation(ρ)/Conjugacy class	{ e }	{} e }	i i }	j. j }	{ k, k }
Representación tripartita	1	1	1	1	1
Representación de firma con i-kernel	1	1	1	−1	−1
Representación de firma con j-kernel	1	1	−1	1	−1
Representación de la firma con cuchilla	1	1	−1	−1	1
2-dimensional representación	2	−2	0	0	0

Desde los personajes irreducibles ${displaystyle chi _{rho }$ en las filas arriba tienen valores reales, esto da la descomposición del álgebra de grupo real ${displaystyle G=mathrm {fnK}$ en ideales mínimos de dos caras:

{displaystyle mathbb {R} [mathrm {Q} _{8}=bigoplus _{rho }(e_{rho }),}

donde los idempotentes ${displaystyle e_{rho }in mathbb {R} [mathrm {Q} _{8}}$ corresponden a los irreducibles:

{displaystyle e_{rho }={frac {dim(rho)}sum _{gin G}chi _{rho }(g^{-1}g,}

para que

{displaystyle {begin{aligned}e_{text{triv} {tfrac} {1}{8}(e+{bar {e}+i+{bar {}+j+{bar} {J}+k+{bar {k})e_{i{text{-ker} {c}} {tfrac}}} {c}} {i} {i}}}} {i}}}}}}} {i}}}}}}}}}\e_ {i} {i} {i} {i}}}}}}}}}}}}}}}}\\\\i}}\\\\\\\\\e_i}}}}}}} {i}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\i}}\\\\\\\\\\\\\\\\\\i}}}}}}}}}}}}}}}}}}}}}}}}} {1}{8}(e+{bar {e}+i+{bar {i}-j-{bar {j}-k-{bar {k})e_{j{text{-ker} {c}} {tfrac}} {1}{8}(e+{bar {e}-i-{bar {}+j+{bar} {j}-k-{bar {k})e_{text{-ker} {fnK}}} {tfrac} {1}{8}(e+{bar {e}-i-{bar {i}-j-{bar {J}+k+{bar {k})e_{2} {2} {2} {2e-2{bar {e})={tfrac {1} {2}(e-{bar {e}})end{aligned}}}} {}} {}} {}} {}} {f} {}}} {f}} {f}}}}}}} {f}} {f}}}}}}} {}}}}}}}}}}}}} {f}}}}}}} {f}}}}}} {f}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}} {f}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Cada uno de estos ideales irreducibles es isomorfo a un álgebra simple central real, los primeros cuatro al campo real ${displaystyle mathbb {R}$ . El último ideal ${displaystyle (e_{2})}$ es isomorfo para el campo de las picaduras ${displaystyle mathbb {H}$ por correspondencia:

{displaystyle {begin{aligned}{tfrac {2} {} {} {} {} {}} {}} {fnMicroc {2} {} {} {i-{b}}} {i- {}})} {m}} {m}} {fnMicroc} {} {}}}} {}}}} {}}}}}}} {m}}}}}} {m}}}}}}}}}} {m}}}}} {m}}}}}}}}}}} {m}}}}}}}}} {m}} {m}}}}} {m}}}}}}}}}} {}}}}}}} {m} {m}}}}}}}}}}} {m}}}} {m}}} {m}}}}}}}}}}}}}} {m}}}}}}}}}}}}} {m}}}}}}}}} {

Además, el homomorfismo de proyección ${displaystyle mathbb {R} [mathrm {Q} _{8}to (e_{2})cong mathbb {H}$ dado por ${displaystyle rmapsto re_{2}$ tiene el kernel ideal generado por el idempotent:

{displaystyle E_{2}{perp }=e_{1}+e_{text{-ker}}}}= {fnfncip}}+e_{text{-ker}}}}={frac {1}{2}(e+{bar {e}})} {}} {c} {c}} {c} {c}}} {c}}}} {c}}}} {c}}}}} {c}} {c}} {c}} {c}}} {c}}}}}}}}}} {c}}}}}}}} {}}}}}}}}} {c}}}}}}}}}} {c}} {c}}}} {c}}}}} {c}}}}}} {c}}}}}}} {c}}}}}} {c}}}}}} {c}}}}}}}}}}}} {c}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

por lo que las cuaterniones también se pueden obtener como el anillo ${displaystyle mathbb {R} [mathrm {Q} _{8}]/(e+{bar {e})cong mathbb {H}$ .

El álgebra de grupo complejo es así ${displaystyle mathbb {C} [mathrm {Q} _{8}]cong mathbb {C} {oplus 4}oplus M_{2}(mathbb {C}}$ Donde ${displaystyle M_{2}(mathbb {C})cong mathbb {H} otimes _{mathbb {R}mathbb {C} cong mathbb {H} oplus mathbb {H}$ es el álgebra de biquaternions.

Representaciones de matrices

Mesa de multiplicación del grupo de cuaternión como subgrupo de SL(2,C). Las entradas están representadas por sectores correspondientes a sus argumentos: 1 (verde), i (azul), −1 (rojo), −i (amarillo).

La representación compleja irreducible bidimensional descrita anteriormente da el grupo de cuaternión Q₈ como subgrupo del grupo lineal general ${displaystyle operatorname {GL} (2,mathbb {C})}$ . El grupo de cuaternión es un subgrupo multiplicativo del álgebra de cuaternión:

{displaystyle mathbb {H} = 'Mathbb {R} 1+Mathbb {R} i+Mathbb {R} j+Mathbb {R} k=mathbb {C} 1+Mathbb {C} j,}

que tiene una representación regular ${displaystyle rho:mathbb {H} to operatorname {M} (2,mathbb {C}}$ por multiplicación izquierda por sí misma considerada como un espacio vectorial complejo con base ${displaystyle {1,j},}$ así ${displaystyle zin mathbb {H}$ corresponde a ${displaystyle mathbb {C}$ - Cartografía lineal ${displaystyle rho _{z}:a+jbmapsto zcdot (a+jb).}$ La representación resultante

{displaystyle {begin{cases}rho:mathrm {Q} _{8}to operatorname {GL} (2,mathbb {C})glongmapsto rho _{g}end{cases}}

está dado por:

{beplaystyle {begin{matrix}emapsto {begin{pmatrix}1}0 âTMa âTMa {

Contenido relacionado

Más resultados...

×	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
i	i	i	e	e	k	k	j	j
i	i	i	e	e	k	k	j	j
j	j	j	k	k	e	e	i	i
j	j	j	k	k	e	e	i	i
k	k	k	j	j	i	i	e	e
k	k	k	j	j	i	i	e	e

×	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
i	i	i	e	e	k	k	j	j
i	i	i	e	e	k	k	j	j
j	j	j	k	k	e	e	i	i
j	j	j	k	k	e	e	i	i
k	k	k	j	j	i	i	e	e
k	k	k	j	j	i	i	e	e

×	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
i	i	i	e	e	k	k	j	j
i	i	i	e	e	k	k	j	j
j	j	j	k	k	e	e	i	i
j	j	j	k	k	e	e	i	i
k	k	k	j	j	i	i	e	e
k	k	k	j	j	i	i	e	e