Gas fermi

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Modelo físico de gases compuesto por muchos fermions no interactores idénticos

Un gas de Fermi ideal es un estado de la materia que es un conjunto de muchos fermiones que no interactúan. Los fermiones son partículas que obedecen a las estadísticas de Fermi-Dirac, como los electrones, los protones y los neutrones y, en general, las partículas con espín semientero. Estas estadísticas determinan la distribución de energía de los fermiones en un gas de Fermi en equilibrio térmico y se caracterizan por su densidad numérica, temperatura y el conjunto de estados de energía disponibles. El modelo lleva el nombre del físico italiano Enrico Fermi.

Este modelo físico se puede aplicar con precisión a muchos sistemas con muchos fermiones. Algunos ejemplos clave son el comportamiento de los portadores de carga en un metal, los nucleones en un núcleo atómico, los neutrones en una estrella de neutrones y los electrones en una enana blanca.

Descripción

Ilustración de los estados energéticos: Diagrama de ocupación energética para un sistema con 7 niveles de energía, la energía

E_{i}

es degenerado

D_{i}

tiempos (hay

D_{i}

estados que tienen una energía

E_{i}

) y tiene una ocupación dada por

N_{i}

, con

{displaystyle i=1,2,3,4,5,6,7}

. Por el principio de exclusión Pauli, hasta

{displaystyle (2j+1)cdot D_{i}}

fermions puede ocupar un nivel de energía

E_{i}

del sistema, donde

j

es la columna de los fermions.

Un gas de Fermi ideal o gas de Fermi libre es un modelo físico que asume una colección de fermiones que no interactúan en un pozo de potencial constante. Los fermiones son partículas elementales o compuestas con espín semientero, por lo que siguen las estadísticas de Fermi-Dirac. El modelo equivalente para partículas de espín entero se denomina gas de Bose (un conjunto de bosones que no interactúan). A una densidad de número de partículas lo suficientemente baja y alta temperatura, tanto el gas de Fermi como el gas de Bose se comportan como un gas ideal clásico.

Según el principio de exclusión de Pauli, ningún estado cuántico puede estar ocupado por más de un fermión con un conjunto idéntico de números cuánticos. Por lo tanto, un gas de Fermi que no interactúa, a diferencia de un gas de Bose, concentra una pequeña cantidad de partículas por energía. Por lo tanto, se prohíbe que un gas de Fermi se condense en un condensado de Bose-Einstein, aunque los gases de Fermi que interactúan débilmente pueden formar un par de Cooper y condensarse (también conocido como régimen de cruce BCS-BEC). La energía total del gas de Fermi en el cero absoluto es mayor que la suma de los estados fundamentales de una sola partícula porque el principio de Pauli implica una especie de interacción o presión que mantiene a los fermiones separados y en movimiento. Por esta razón, la presión de un gas de Fermi es distinta de cero incluso a temperatura cero, en contraste con la de un gas ideal clásico. Por ejemplo, esta llamada presión de degeneración estabiliza una estrella de neutrones (un gas de Fermi de neutrones) o una estrella enana blanca (un gas de Fermi de electrones) contra la atracción de la gravedad, que aparentemente colapsaría la estrella en un agujero negro. Solo cuando una estrella es lo suficientemente masiva para superar la presión de degeneración puede colapsar en una singularidad.

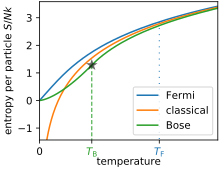
Es posible definir una temperatura de Fermi por debajo de la cual el gas puede considerarse degenerado (su presión deriva casi exclusivamente del principio de Pauli). Esta temperatura depende de la masa de los fermiones y de la densidad de los estados de energía.

La suposición principal del modelo de electrones libres para describir los electrones deslocalizados en un metal puede derivarse del gas de Fermi. Dado que las interacciones se desprecian debido al efecto de pantalla, el problema de tratar las propiedades de equilibrio y la dinámica de un gas de Fermi ideal se reduce al estudio del comportamiento de partículas individuales independientes. En estos sistemas, la temperatura de Fermi es generalmente de muchos miles de Kelvin, por lo que en aplicaciones humanas el gas de electrones puede considerarse degenerado. La energía máxima de los fermiones a temperatura cero se denomina energía de Fermi. La superficie de energía de Fermi en el espacio recíproco se conoce como superficie de Fermi.

El modelo de electrones casi libres adapta el modelo de gas de Fermi para tener en cuenta la estructura cristalina de metales y semiconductores, donde los electrones de una red cristalina se sustituyen por electrones de Bloch con el momento cristalino correspondiente. Como tal, los sistemas periódicos todavía son relativamente manejables y el modelo constituye el punto de partida para teorías más avanzadas que se ocupan de las interacciones, p. utilizando la teoría de la perturbación.

Gas uniforme 1D

El pozo cuadrado infinito unidimensional de longitud L es un modelo para una caja unidimensional con la energía potencial:

<math alttext="{displaystyle V(x)={begin{cases}0,&x_{c}-{tfrac {L}{2}}<xV()x)={}0,xc− − L2.x.xc+L2,JUEGO JUEGO ,De lo contrario.{displaystyle V(x)={begin{cases}0, recurx_{c}-{tfrac {L}{2} Secuestró en el texto {L}{2},\\\infty mutuamente}end{cases}}<img alt="{displaystyle V(x)={begin{cases}0,&x_{c}-{tfrac {L}{2}}<x

Es un modelo-sistema estándar en mecánica cuántica cuya solución para una sola partícula es bien conocida. Dado que el potencial dentro de la caja es uniforme, este modelo se denomina gas uniforme 1D, aunque el perfil de densidad numérica real del gas puede tener nodos y antinodos cuando el número total de partículas es pequeño.

Los niveles están etiquetados por un solo número cuántico n y las energías están dadas por:

{displaystyle E_{n}=E_{0}+{frac {hbar ^{2}pi ^{2}}{2mL^{2}}}n^{2}.}

E_{0}

m

hbar

Para N fermions con spin-1⁄2 en la caja, no más de dos partículas pueden tener la misma energía, es decir, dos partículas pueden tener la energía de ${textstyle E_{1}}$ , otras dos partículas pueden tener energía ${textstyle E_{2}}$ y así sucesivamente. Las dos partículas de la misma energía tienen giro 1.2 (spin up) o1.2 (spin down), conduciendo a dos estados para cada nivel de energía. En la configuración para la que la energía total es más baja (el estado del suelo), todos los niveles de energía hasta n=N/2 están ocupados y todos los niveles superiores están vacíos.

Definición de la referencia para la energía fermi $E_{0}$ , la energía fermi es dada por

{displaystyle E_{mathrm {F} }^{({text{1D}})}=E_{n}-E_{0}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}left(leftlfloor {frac {N}{2}}rightrfloor right)^{2},}

{textstyle leftlfloor {frac {N}{2}}rightrfloor }

Límite termodinámico

En el límite termodinámico, el número total de partículas N es tan grande que el número cuántico n puede tratarse como una variable continua. En este caso, el perfil de densidad numérica general en la caja es realmente uniforme.

El número de estados cuánticos en el rango $<math alttext="{displaystyle n_{1}<nn1.n.n1+dn{displaystyle No.<img alt="{displaystyle n_{1}<n$ es:

{displaystyle D_{n}(n_{1}),dn=2,dn,.}

Sin pérdida de generalidad, se elige que la energía de punto cero sea cero, con el siguiente resultado:

{displaystyle E_{n}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}n^{2}implies dE={frac {hbar ^{2}pi ^{2}}{mL^{2}}}n,dn={frac {hbar pi }{L}}{sqrt {frac {2E}{m}}}dn,.}

Por lo tanto, en el rango:

<math alttext="{displaystyle E_{1}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}n_{1}^{2}<EE1=▪ ▪ 2π π 22mL2n12.E.E1+dE,{displaystyle E_{1}={hbar ^{2}pi ¿Qué?<img alt="{displaystyle E_{1}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}n_{1}^{2}<E

{displaystyle D_{n}(n_{1}),dn=2{frac {dE}{dE/dn}}={frac {2}{{frac {hbar ^{2}pi ^{2}}{mL^{2}}}n}},dEequiv D(E_{1}),dE,.}

Aquí, el grado de degeneración es:

{displaystyle D(E)={frac {2}{dE/dn}}={frac {2L}{hbar pi }}{sqrt {frac {m}{2E}}},.}

Y la densidad de estados es:

{displaystyle g(E)equiv {frac {1}{L}}D(E)={frac {2}{hbar pi }}{sqrt {frac {m}{2E}}},.}

En la literatura moderna, lo anterior $D(E)$ a veces también se llama la "densidad de estados". Sin embargo, $g(E)$ difiere de $D(E)$ por un factor del volumen del sistema (que es $L$ en este caso 1D).

Basado en la siguiente fórmula:

{displaystyle int _{0}^{E_{mathrm {F} }}D(E),dE=N,,}

La energía de Fermi en el límite termodinámico se puede calcular como:

{displaystyle E_{mathrm {F} }^{({text{1D}})}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}left({frac {N}{2}}right)^{2},.}

Gas uniforme 3D

Un modelo del núcleo atómico que lo muestra como un paquete compacto de los dos tipos de núcleos: protones (rojo) y neutrones (azul). Como primera aproximación, el núcleo se puede tratar como compuesto de protón no interaccionante y gases de neutrones.

La caja de gas de Fermi uniforme tridimensional isotrópica y no relativista se conoce como esfera de Fermi.

Un pozo cuadrado infinito tridimensional (es decir, una caja cúbica que tiene una longitud lateral L) tiene la energía potencial

<math alttext="{displaystyle V(x,y,z)={begin{cases}0,&-{frac {L}{2}}<x,y,zV()x,Sí.,z)={}0,− − L2.x,Sí.,z.L2,JUEGO JUEGO ,De lo contrario.{displaystyle V(x,y,z)={begin{cases}0, reducida-{frac {L}{2}}cantax,y,z secuestró {frac {L}{2},\\\infty limit {text{otherwise.}}end{cases}}}}}}}}}}}<img alt="{displaystyle V(x,y,z)={begin{cases}0,&-{frac {L}{2}}<x,y,z

Los estados ahora están etiquetados por tres números cuánticos n_x, n_y y n_z. Las energías de una sola partícula son

{displaystyle E_{n_{x},n_{y},n_{z}}=E_{0}+{frac {hbar ^{2}pi ^{2}}{2mL^{2}}}left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}right),,}

n_xn_Sí.n_z

E_{211}=E_{121}=E_{112}

Límite termodinámico

Cuando la caja contiene N fermiones de espín ½ que no interactúan, es interesante calcular la energía en el límite termodinámico, donde N es tan grande que el cuanto números n_x, n_y, n_z pueden tratarse como variables continuas.

Con el vector ${displaystyle mathbf {n} =(n_{x},n_{y},n_{z})}$ , cada estado cuántico corresponde a un punto en 'n-espacio' con energía

{displaystyle E_{mathbf {n} }=E_{0}+{frac {hbar ^{2}pi ^{2}}{2mL^{2}}}|mathbf {n} |^{2},}

Con ${displaystyle |mathbf {n} |^{2}}$ denotando la plaza de la longitud Euclideana habitual ${displaystyle |mathbf {n} |={sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}}$ . El número de estados con energía menos que E_F+E₀ es igual al número de estados que se encuentran dentro de una esfera de radio ${displaystyle |mathbf {n} _{mathrm {F} }|}$ en la región de n-espacio donde n_x, n_Sí., n_z son positivos. En el estado del suelo este número es igual al número de helechos en el sistema:

{displaystyle N=2times {frac {1}{8}}times {frac {4}{3}}pi n_{mathrm {F} }^{3}}

Los fermions libres que ocupan los estados energéticos más bajos forman una esfera en el espacio recíproco. La superficie de esta esfera es la superficie de Fermi.

El factor de dos expresa los dos estados de espín, y el factor de 1/8 expresa la fracción de la esfera que se encuentra en la región donde todos los n son positivos.

{displaystyle n_{mathrm {F} }=left({frac {3N}{pi }}right)^{1/3}}

Fermi energy

{displaystyle E_{mathrm {F} }={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}n_{mathrm {F} }^{2}={frac {hbar ^{2}pi ^{2}}{2mL^{2}}}left({frac {3N}{pi }}right)^{2/3}}

Lo que resulta en una relación entre la energía de Fermi y el número de partículas por volumen (cuando L² se reemplaza por V^2/3):

{displaystyle E_{mathrm {F} }={frac {hbar ^{2}}{2m}}left({frac {3pi ^{2}N}{V}}right)^{2/3}}

Esta es también la energía de la partícula de máxima energía (la $N$ a partícula), por encima de la energía de punto cero $E_{0}$ . El $N'$ la partícula tiene una energía

{displaystyle E_{N'}=E_{0}+{frac {hbar ^{2}}{2m}}left({frac {3pi ^{2}N'}{V}}right)^{2/3},=E_{0}+E_{mathrm {F} }{big |}_{N'}}

La energía total de una esfera fermi $N$ fermions (que ocupan todos los $N$ estados energéticos dentro de la esfera fermi) es dado por:

{displaystyle E_{rm {T}}=NE_{0}+int _{0}^{N}E_{mathrm {F} }{big |}_{N'},dN'=left({frac {3}{5}}E_{mathrm {F} }+E_{0}right)N}

Por lo tanto, la energía promedio por partícula viene dada por:

{displaystyle E_{mathrm {av} }=E_{0}+{frac {3}{5}}E_{mathrm {F} }}

Densidad de estados

Densidad de estados (DOS) de un gas fermi en 3-dimensiones

Para el gas fermi uniforme 3D, con fermions de spin-1⁄2, el número de partículas como función de la energía ${textstyle N(E)}$ se obtiene sustituyendo la energía Fermi por una energía variable ${textstyle (E-E_{0})}$ :

{displaystyle N(E)={frac {V}{3pi ^{2}}}left[{frac {2m}{hbar ^{2}}}(E-E_{0})right]^{3/2},}

de la cual la densidad de estados (número de estados energéticos por volumen) $g(E)$ se puede obtener. Puede calcularse diferenciando el número de partículas con respecto a la energía:

{displaystyle g(E)={frac {1}{V}}{frac {partial N(E)}{partial E}}={frac {1}{2pi ^{2}}}left({frac {2m}{hbar ^{2}}}right)^{3/2}{sqrt {E-E_{0}}}.}

Este resultado proporciona una manera alternativa de calcular la energía total de una esfera fermi $N$ fermions (que ocupan todos los $N$ estados energéticos dentro de la esfera fermi:

{displaystyle {begin{aligned}E_{T}&=int _{0}^{N}Emathrm {d} N(E)=EN(E){big |}_{0}^{N}-int _{E_{0}}^{E_{0}+E_{F}}N(E)mathrm {d} E\&=(E_{0}+E_{F})N-int _{0}^{E_{F}}N(E)mathrm {d} (E-E_{0})\&=(E_{0}+E_{F})N-{frac {2}{5}}E_{F}N(E_{F})=left(E_{0}+{frac {3}{5}}E_{mathrm {F} }right)Nend{aligned}}}

Magnitudes termodinámicas

Presión de degeneración

Presión vs curvas de temperatura de los gases ideales clásicos y cuánticos (gas Fremi, gas Bose) en tres dimensiones. La repulsión de Pauli en fermions (como electrones) les da una presión adicional sobre un gas clásico equivalente, más significativamente a baja temperatura.

Usando la primera ley de la termodinámica, esta energía interna se puede expresar como una presión, es decir

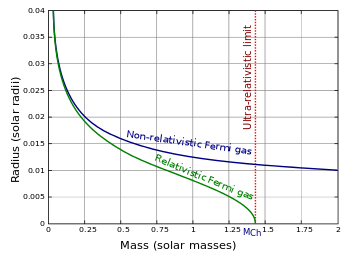
{displaystyle P=-{frac {partial E_{rm {T}}}{partial V}}={frac {2}{5}}{frac {N}{V}}E_{mathrm {F} }={frac {(3pi ^{2})^{2/3}hbar ^{2}}{5m}}left({frac {N}{V}}right)^{5/3},}

presión de degeneración

Las estrellas estándar evitan el colapso al equilibrar la presión térmica (plasma y radiación) con las fuerzas gravitatorias. Al final de la vida de la estrella, cuando los procesos térmicos son más débiles, algunas estrellas pueden convertirse en enanas blancas, que solo se sostienen contra la gravedad por la presión de degeneración de los electrones. Usando el gas de Fermi como modelo, es posible calcular el límite de Chandrasekhar, es decir, la masa máxima que cualquier estrella puede adquirir (sin una presión térmica significativa) antes de colapsar en un agujero negro o una estrella de neutrones. Esta última, es una estrella compuesta principalmente por neutrones, donde el colapso también se evita por presión de degeneración de neutrones.

Para el caso de los metales, la presión de degeneración electrónica contribuye a la compresibilidad o módulo volumétrico del material.

Potencial químico

Suponiendo que la concentración de helechos no cambie con la temperatura, entonces el potencial químico total μ (nivel fermi) del gas fermi ideal tridimensional está relacionado con la energía fermi de temperatura cero E_F por una expansión Sommerfeld (suponiendo ${displaystyle k_{rm {B}}Tll E_{mathrm {F} }}$ ):

{displaystyle mu (T)=E_{0}+E_{mathrm {F} }left[1-{frac {pi ^{2}}{12}}left({frac {k_{rm {B}}T}{E_{mathrm {F} }}}right)^{2}-{frac {pi ^{4}}{80}}left({frac {k_{rm {B}}T}{E_{mathrm {F} }}}right)^{4}+cdots right],}

Por lo tanto, el potencial químico interno, µ-E₀, es aproximadamente igual a la energía de Fermi a temperaturas mucho más bajas que la temperatura característica de Fermi T_F. Esta temperatura característica es del orden de 10⁵ K para un metal, por lo que a temperatura ambiente (300 K), la energía de Fermi y el potencial químico interno son esencialmente equivalentes.

Valores típicos

Metales

Bajo el modelo de electrones gratis, los electrones de un metal se pueden considerar para formar un gas fermi uniforme. La densidad del número $N/V$ de electrones de conducción en metales oscila entre aproximadamente 10²⁸ y 10²⁹ electrones por m³, que es también la densidad típica de los átomos en materia sólida ordinaria. Esta densidad de número produce una energía fermi del orden:

{displaystyle E_{mathrm {F} }={frac {hbar ^{2}}{2m_{e}}}left(3pi ^{2} 10^{28 sim 29} mathrm {m^{-3}} right)^{2/3}approx 2 sim 10 mathrm {eV}}

m_e⁶T_F

Enanas blancas

Las estrellas conocidas como enanas blancas tienen una masa comparable a la del Sol, pero tienen alrededor de una centésima parte de su radio. Las altas densidades significan que los electrones ya no están unidos a núcleos individuales y en su lugar forman un gas de electrones degenerado. La densidad numérica de electrones en una enana blanca es del orden de 10³⁶ electrones/m³. Esto significa que su energía de Fermi es:

{displaystyle E_{mathrm {F} }={frac {hbar ^{2}}{2m_{e}}}left({frac {3pi ^{2}(10^{36})}{1 mathrm {m^{3}} }}right)^{2/3}approx 3times 10^{5} mathrm {eV} =0.3 mathrm {MeV} }

Núcleo

Otro ejemplo típico es el de las partículas en el núcleo de un átomo. El radio del núcleo es aproximadamente:

{displaystyle R=left(1.25times 10^{-15}mathrm {m} right)times A^{1/3}}

La densidad numérica de nucleones en un núcleo es por lo tanto:

{displaystyle rho ={frac {A}{{frac {4}{3}}pi R^{3}}}approx 1.2times 10^{44} mathrm {m^{-3}} }

Esta densidad hay que dividirla por dos, porque la energía de Fermi solo se aplica a fermiones del mismo tipo. La presencia de neutrones no afecta la energía de Fermi de los protones en el núcleo y viceversa.

La energía de Fermi de un núcleo es aproximadamente:

{displaystyle E_{mathrm {F} }={frac {hbar ^{2}}{2m_{rm {p}}}}left({frac {3pi ^{2}(6times 10^{43})}{1 mathrm {m} ^{3}}}right)^{2/3}approx 3times 10^{7} mathrm {eV} =30 mathrm {MeV}}

m_p

El radio del núcleo admite desviaciones en torno al valor mencionado anteriormente, por lo que un valor típico para la energía de Fermi suele ser de 38 MeV.

Gas uniforme de dimensión arbitraria

Densidad de estados

Usando un volumen integral ${textstyle d}$ dimensiones, la densidad de estados es:

{displaystyle g^{(d)}(E)=g_{s}int {frac {mathrm {d} ^{d}mathbf {k} }{(2pi)^{d}}}delta left(E-E_{0}-{frac {hbar ^{2}|mathbf {k} |^{2}}{2m}}right)=g_{s} left({frac {m}{2pi hbar ^{2}}}right)^{d/2}{frac {(E-E_{0})^{d/2-1}}{Gamma (d/2)}}}

La energía de Fermi se obtiene buscando la densidad numérica de las partículas:

{displaystyle rho ={frac {N}{V}}=int _{E_{0}}^{E_{0}+E_{mathrm {F} }^{(d)}}g^{(d)}(E),dE}

Para obtener:

{displaystyle E_{mathrm {F} }^{(d)}={frac {2pi hbar ^{2}}{m}}left({tfrac {1}{g_{s}}}Gamma left({tfrac {d}{2}}+1right){frac {N}{V}}right)^{2/d}}

{textstyle V}

{textstyle g_{s}}

{textstyle g_{s}=2}

Se obtiene un resultado particular para $d=2$ , donde la densidad de estados se convierte en una constante (no depende de la energía):

{displaystyle g^{(2mathrm {D})}(E)={frac {g_{s}}{2}}{frac {m}{pi hbar ^{2}}}.}

Gas Fermi en trampa armónica

El potencial de trampa armónica:

{displaystyle V(x,y,z)={frac {1}{2}}momega _{x}^{2}x^{2}+{frac {1}{2}}momega _{y}^{2}y^{2}+{frac {1}{2}}momega _{z}^{2}z^{2}}

es un sistema modelo con muchas aplicaciones en la física moderna. La densidad de estados (o más exactamente, el grado de degeneración) para una determinada especie de espín es:

{displaystyle g(E)={frac {E^{2}}{2(hbar omega _{text{ho}})^{3}}},,}

Donde ${displaystyle omega _{text{ho}}={sqrt[{3}]{omega _{x}omega _{y}omega _{z}}}}$ es la frecuencia de oscilación armónica.

La energía de Fermi para una determinada especie de espín es:

{displaystyle E_{rm {F}}=(6N)^{1/3}hbar omega _{text{ho}},.}

Cantidades de Fermi relacionadas

En relación con la energía de Fermi, algunas cantidades útiles también aparecen a menudo en la literatura moderna.

El Temperatura de fermi se define como ${textstyle T_{mathrm {F} }={frac {E_{mathrm {F} }}{k_{rm {B}}}}}$ , donde $k_{rm B}$ es la constante de Boltzmann. La temperatura de Fermi se puede considerar como la temperatura a la que los efectos térmicos son comparables a los efectos cuánticos asociados con las estadísticas de Fermi. La temperatura de Fermi para un metal es un par de órdenes de magnitud sobre la temperatura ambiente. Otras cantidades definidas en este contexto Momento de fermi ${textstyle p_{mathrm {F} }={sqrt {2mE_{mathrm {F} }}}}$ , y Velocidad de fermi ${textstyle v_{mathrm {F} }={frac {p_{mathrm {F} }}{m}}}$ , que son el impulso y la velocidad del grupo, respectivamente, de un fermión en la superficie de Fermi. El impulso de Fermi también se puede describir como ${displaystyle p_{mathrm {F} }=hbar k_{mathrm {F} }}$ , donde ${displaystyle k_{mathrm {F} }}$ es el radio de la esfera fermi y se llama el vector de onda fermi.

Tenga en cuenta que estas cantidades no están bien definidas en los casos en que la superficie de Fermi no es esférica.

Tratamiento a temperatura finita

Gran conjunto canónico

La mayoría de los cálculos anteriores son exactos a cero temperatura, pero permanecen como buenas aproximaciones para temperaturas inferiores a la temperatura de Fermi. Para otras variables termodinámicas es necesario escribir un potencial termodinámico. Para un conjunto de fermiones idénticos, la mejor manera de derivar un potencial es del gran conjunto canónico con temperatura fija, volumen y potencial químico μ. La razón se debe al principio de exclusión de Pauli, ya que los números de ocupación de cada estado cuántico son dados por 1 o 0 (ya hay un electrón ocupando el estado o no), por lo que la función de partición (grand) ${displaystyle {mathcal {Z}}}$ puede ser escrito como

{displaystyle {mathcal {Z}}(T,V,mu)=sum _{{q}}e^{-beta (E_{q}-mu N_{q})}=prod _{q}sum _{n_{q}=0}^{1}e^{-beta (varepsilon _{q}-mu)n_{q}}=prod _{q}left(1+e^{-beta (varepsilon _{q}-mu)}right),}

Donde ${displaystyle beta ^{-1}=k_{rm {B}}T}$ , ${displaystyle {q}}$ indexa los conjuntos de todos los microstates posibles que dan la misma energía total ${textstyle E_{q}=sum _{q}varepsilon _{q}n_{q}}$ y número de partículas ${textstyle N_{q}=sum _{q}n_{q}}$ , ${textstyle varepsilon _{q}}$ es la única energía de partículas del estado ${textstyle q}$ (conta dos veces si la energía del estado es degenerada) y ${textstyle n_{q}=0,1}$ , su ocupación. Así el gran potencial está escrito como

{displaystyle Omega (T,V,mu)=-k_{rm {B}}Tln left({mathcal {Z}}right)=-k_{rm {B}}Tsum _{q}ln left(1+e^{beta (mu -varepsilon _{q})}right).}

El mismo resultado se puede obtener en el conjunto canónico y microcanónico, ya que el resultado de cada conjunto debe dar el mismo valor al límite termodinámico ${textstyle (N/Vrightarrow infty)}$ . El gran conjunto canónico se recomienda aquí ya que evita el uso de combinatoria y factorial.

Como se exploró en secciones anteriores, en el límite macroscópico podemos usar una aproximación continua (aproximación de Thomas-Fermi) para convertir esta suma en una integral:

{displaystyle Omega (T,V,mu)=-k_{rm {B}}Tint _{-infty }^{infty }D(varepsilon)ln left(1+e^{beta (mu -varepsilon)}right),dvarepsilon }

D () ε)

Relación con la distribución de Fermi-Dirac

El gran potencial está relacionado con el número de partículas a temperatura finita de la siguiente manera

{displaystyle N=-left({frac {partial Omega }{partial mu }}right)_{T,V}=int _{-infty }^{infty }D(varepsilon){mathcal {f}}left({frac {varepsilon -mu }{k_{rm {B}}T}}right),mathrm {d} varepsilon }

{displaystyle {mathcal {f}}(x)={frac {1}{e^{x}+1}}}

Del mismo modo, la energía interna total es

{displaystyle U=Omega -Tleft({frac {partial Omega }{partial T}}right)_{V,mu }-mu left({frac {partial Omega }{partial mu }}right)_{T,V}=int _{-infty }^{infty }D(varepsilon){mathcal {f}}!left({frac {varepsilon -mu }{k_{rm {B}}T}}right)varepsilon ,dvarepsilon.}

Solución exacta para ley de potencias de densidad de estados

Curvas de temperatura entropía vs de gas ideal clásico y gases ideales cuánticos (gas Fremi, gas de Bose) en tres dimensiones (

α

= 1,5) con constante

N, V

Muchos sistemas de interés tienen una densidad total de estados con la forma de ley de potencia:

{displaystyle D(varepsilon)=Vg(varepsilon)={frac {Vg_{0}}{Gamma (alpha)}}(varepsilon -varepsilon _{0})^{alpha -1},qquad varepsilon geq varepsilon _{0}}

g 0

α

ε 0

d

$α = d /2$ para partículas no relativistas en $d$ - caja dimensional,
$α = d$ para partículas no relativistas en $d$ - potencial armónico dimensional bien,
$α = d$ para partículas hiper-relativistas en un $d$ - caja dimensional.

Para tal densidad de estados de ley de potencia, la integral de gran potencial se evalúa exactamente como:

{displaystyle Omega (T,V,mu)=-Vg_{0}(k_{rm {B}}T)^{alpha +1}F_{alpha }left({frac {mu -varepsilon _{0}}{k_{rm {B}}T}}right),}

{displaystyle F_{alpha }(x)}

Extensiones al modelo

Gas de Fermi relativista

Relaciones radio-masa para un enano blanco modelo, relación relativista vs no-relativista. El límite Chandrasekhar se indica como M_Ch.

El artículo solo ha tratado el caso en que las partículas tienen una relación parabólica entre energía y cantidad de movimiento, como es el caso de la mecánica no relativista. Para partículas con energías cercanas a su respectiva masa en reposo, son aplicables las ecuaciones de la relatividad especial. Donde la energía de una sola partícula viene dada por:

{displaystyle E={sqrt {(pc)^{2}+(mc^{2})^{2}}}.}

Para este sistema, la energía de Fermi viene dada por:

{displaystyle E_{mathrm {F} }={sqrt {(p_{mathrm {F} }c)^{2}+(mc^{2})^{2}}}-mc^{2}approx p_{mathrm {F} }c,}

approx

{displaystyle p_{mathrm {F} }=hbar left({frac {1}{g_{s}}}6pi ^{2}{frac {N}{V}}right)^{1/3}.}

El modelo relativista de gas Fermi también se utiliza para la descripción de grandes enanas blancas que están cerca del límite Chandresekhar. Para el caso ultrarelativista, la presión de degeneración es proporcional a ${displaystyle (N/V)^{4/3}}$ .

Líquido Fermi

En 1956, Lev Landau desarrolló la teoría del líquido de Fermi, donde trató el caso de un líquido de Fermi, es decir, un sistema con interacciones repulsivas, no necesariamente pequeñas, entre fermiones. La teoría muestra que las propiedades termodinámicas de un gas de Fermi ideal y un líquido de Fermi no difieren mucho. Se puede demostrar que el líquido de Fermi es equivalente a un gas de Fermi compuesto por excitaciones colectivas o cuasipartículas, cada una con diferente masa efectiva y momento magnético.

Contenido relacionado

Más resultados...