Función monótona

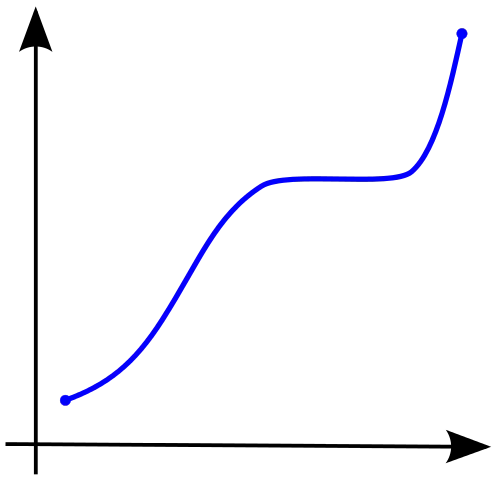
Una función monótona es una función que mantiene constante la relación de orden del conjunto de valores de salida de la función. Dicho de forma más sencilla, las funciones monótonas son aquellas que crecen o decrecen de forma constante. Este concepto tuvo sus orígenes en el cálculo, y se ha expandido y aplicado en áreas más abstractas como la teoría del orden.

Una función es considerada monótona cuando, al aplicarse entre dos conjuntos ordenados, conserva o invierte la relación de orden existente entre ellos. Si la función mantiene la relación de orden, es decir, si a un elemento mayor en el conjunto de origen le corresponde un elemento mayor o igual en el conjunto de destino, se la denomina "función monótona creciente". Por otro lado, si la función invierte esta relación, es decir, a un elemento mayor le corresponde un elemento menor o igual, se la conoce como "función monótona decreciente".

Es importante destacar que en ocasiones se usa el término "estrictamente" para hacer énfasis en que la función es inyectiva, lo que significa que a elementos distintos en el conjunto de origen les corresponden elementos distintos en el conjunto de destino. Aunque en muchos contextos matemáticos este detalle se considera implícito. Las funciones monótonas son herramientas que proporcionan una estructura esencial para el análisis y la comprensión de las relaciones entre conjuntos ordenados.

HSD

En cálculo y análisis

En cálculo, una función definido en un subconjunto de los números reales con valores reales se llama monotónico si y sólo si es totalmente no creciente, o totalmente no-creciente. Es decir, según Fig. 1, una función que aumenta monotonicamente no tiene que aumentar exclusivamente, simplemente no debe disminuir.

Una función se llama monotonicamente aumentando (también creciente o no disminución) si para todos x{displaystyle x} y Sí.{displaystyle y} tales que x≤ ≤ Sí.{displaystyle xleq y} uno tiene f()x)≤ ≤ f()Sí.){displaystyle f!left(xright)leq f!left(yright)}Así que f{displaystyle f} preserva el orden (ver Figura 1). Asimismo, una función se llama monotonicamente disminuyendo (también disminución o no crecienteSi, cuando sea x≤ ≤ Sí.{displaystyle xleq y}, entonces f()x)≥ ≥ f()Sí.){displaystyle f!left(xright)geq f!left(yright)}Así que inversas la orden (ver Figura 2).

Si la orden ≤ ≤ {displaystyle leq } en la definición de monotónica es reemplazada por el orden estricto <math alttext="{displaystyle .{displaystyle]<img alt=", uno obtiene un requisito más fuerte. Una función con esta propiedad se llama Aumento estricto (también creciente). Una vez más, al invertir el símbolo del orden, se encuentra un concepto correspondiente llamado Reducción estricta (también disminución). Una función con cualquiera de los bienes se llama estrictamente monotone. Las funciones que son estrictamente monotonas son una a una (porque para x{displaystyle x} no igual a Sí.{displaystyle y}, o, por lo tanto f()x)ل ل f()Sí.){displaystyle f!left(xright)neq f!left(yright)}.)

Para evitar la ambigüedad, los términos débilmente monótono, débilmente creciente y débilmente decreciente se utilizan a menudo para referirse a la monotonicidad no estricta.

Los términos "no decrecientes" y "no creciente" no debe confundirse con las calificaciones negativas (mucho más débiles) "no decrecientes" y "no aumentando". Por ejemplo, la función no monótona que se muestra en la figura 3 primero cae, luego sube y luego vuelve a caer. Por lo tanto, no es decreciente ni creciente, pero no es ni decreciente ni decreciente.

Una función f()x){displaystyle f!left(xright)} se dice que absolutamente monotónico sobre un intervalo ()a,b){displaystyle left(a,bright)} si los derivados de todas las órdenes f{displaystyle f} son no negativas o no positivas en todos los puntos del intervalo.

Inversa de la función

Todas las funciones estrictamente monótonas son invertibles porque se garantiza que tienen un mapeo uno a uno desde su rango hasta su dominio.

Sin embargo, las funciones que son solo débilmente monótonas no son invertibles porque son constantes en algún intervalo (y por lo tanto no son uno a uno).

Una función puede ser estrictamente monotónica sobre un rango limitado de valores y por lo tanto tener un inverso en ese rango, aunque no sea estrictamente monotónico en todas partes. Por ejemplo, si Sí.=g()x){displaystyle y=g(x)} está aumentando estrictamente en el rango [a,b]{displaystyle [a,b]}, entonces tiene un inverso x=h()Sí.){displaystyle x=h(y)} en el rango [g()a),g()b)]{displaystyle [g(a),g(b)}.

Tenga en cuenta que el término monotónico a veces se usa en lugar de estrictamente monótono, por lo que una fuente puede afirmar que todas las funciones monotónicas son invertibles cuando en realidad significan que todas son estrictamente monótonas. Las funciones son invertibles.

Transformación monótona

El término transformación monótona (o transformación monótona) también puede causar confusión porque se refiere a una transformación por una función estrictamente creciente. Este es el caso en economía con respecto a las propiedades ordinales de una función de utilidad que se conserva a través de una transformada monótona (ver también preferencias monótonas). En este contexto, el término "transformación monótona" se refiere a una transformación monótona positiva y pretende distinguirla de una "transformación monótona negativa", que invierte el orden de los números.

Algunas aplicaciones y resultados básicos

Las siguientes propiedades son verdaderas para una función monotónica f:: R→ → R{displaystyle fcolon mathbb {R} to mathbb {R}:

• f{displaystyle f} tiene límites de la derecha y de la izquierda en cada punto de su dominio;
• f{displaystyle f} tiene un límite en el infinito positivo o negativo (± ± JUEGO JUEGO {displaystyle pm infty }de un número real, JUEGO JUEGO {displaystyle infty }, o − − JUEGO JUEGO {displaystyle -infty }.
• f{displaystyle f} sólo pueden tener discontinuidades de salto;
• f{displaystyle f} sólo puede tener muchas discontinuidades en su dominio. Las discontinuidades, sin embargo, no consisten necesariamente en puntos aislados e incluso pueden ser densos en un intervalo (a, b). Por ejemplo, para cualquier secuencia summable ()ai)(a_{i}) de números positivos y cualquier enumeración ()qi){displaystyle (q_{i})} de los números racionales, la función monotonicamente creciente
  f()x)=.. qi≤ ≤ xai{displaystyle f(x)=sum _{q_{i}leq #

  

  es continua exactamente en cada número irracional (cf. cuadro). Es la función de distribución acumulativa de la medida discreta sobre los números racionales, donde ai{displaystyle A_{i} es el peso de qi{displaystyle q_{i}.

Estas propiedades son la razón por la que las funciones monótonas son útiles en el trabajo técnico de análisis. Otras propiedades importantes de estas funciones incluyen:

• si f{displaystyle f} es una función monotónica definida en un intervalo I{displaystyle Yo..., entonces f{displaystyle f} es diferente casi en todas partes I{displaystyle Yo...; es decir, el conjunto de números x{displaystyle x} dentro I{displaystyle Yo... tales que f{displaystyle f} no es diferente en x{displaystyle x} Lebesgue mide cero. Además, este resultado no puede ser mejorado para contar: ver función Cantor.
• si este set es contable, entonces f{displaystyle f} es absolutamente continuo
• si f{displaystyle f} es una función monotónica definida en un intervalo [a,b]{displaystyle left[a,bright], entonces f{displaystyle f} Riemann es integrador.

Una aplicación importante de las funciones monotónicas está en la teoría de la probabilidad. Si X{displaystyle X} es una variable aleatoria, su función de distribución acumulativa FX()x)=Prob()X≤ ≤ x){displaystyle F_{X}!left(xright)={text{Prob}!left(Xleq xright)} es una función monotonicamente creciente.

Una función es unimodal si crece monótonamente hasta cierto punto (la moda) y luego decrece monótonamente.

Cuando f{displaystyle f} es un estrictamente monotónico función, entonces f{displaystyle f} es inyectable en su dominio, y si T{displaystyle T} es el rango de f{displaystyle f}, entonces hay una función inversa en T{displaystyle T} para f{displaystyle f}. En contraste, cada función constante es monotónica, pero no injetiva, y por lo tanto no puede tener un inverso.

En topología

A map f:X→ → Y{displaystyle f:Xto Sí. se dice que monotone si cada una de sus fibras está conectada; es decir, para cada elemento Sí.▪ ▪ Y,{displaystyle yin Y,} el conjunto (posiblemente vacío) f− − 1()Sí.){displaystyle f^{-1}(y)} es un subespacio conectado X.{displaystyle X.}

En análisis funcional

En el análisis funcional en un espacio vectorial topológico X{displaystyle X}, un operador (posiblemente no lineal) T:X→ → XAlternativa Alternativa {displaystyle T:Xrightarrow X^{*} se dice que es un monotone operator si

()Tu− − Tv,u− − v)≥ ≥ 0О О u,v▪ ▪ X.{displaystyle (Tu-Tv,u-v)geq 0quadforall u,vin X.}

El teorema de Kachurovskii muestra que las funciones convexas en espacios de Banach tienen operadores monótonos como sus derivados.

Un subconjunto G{displaystyle G. de X× × XAlternativa Alternativa {displaystyle Xtimes X^{*} se dice que es un monotone set si por cada par [u1,w1]{displaystyle [u_{1},w_{1} y [u2,w2]{displaystyle [u_{2},w_{2} dentro G{displaystyle G.,

()w1− − w2,u1− − u2)≥ ≥ 0.{displaystyle (w_{1}-w_{2},u_{1}-u_{2})geq 0.}

G{displaystyle G. se dice que monotone maximal si es maximal entre todos los conjuntos de monotona en el sentido de la inclusión de conjunto. El gráfico de un operador de monotonía G()T){displaystyle G(T)} es un juego de monotonas. Se dice que un operador de monotonía monotone maximal si su gráfico es un Set de monotonía maximal.

En la teoría del orden

La teoría del orden trata con conjuntos arbitrarios parcialmente ordenados y conjuntos preordenados como una generalización de los números reales. La definición anterior de monotonicidad también es relevante en estos casos. Sin embargo, los términos "aumentando" y "disminuyendo" se evitan, ya que su representación pictórica convencional no se aplica a órdenes que no son totales. Además, las estrictas relaciones < y > son de poca utilidad en muchos pedidos no totales y, por lo tanto, no se introduce terminología adicional para ellos.

Haciendo que ≤ denote la relación de orden parcial de cualquier conjunto parcialmente ordenado, una función monótona, también llamada isotona, o order-preserving, satisface la propiedad

x ≤ Sí. implicación f()x≤ f()Sí.),

para todo x e y en su dominio. El compuesto de dos mapeos monótonos también es monótono.

La noción dual a menudo se denomina antitono, antimonótono o inversión de orden. Por lo tanto, una función de antitono f satisface la propiedad

x ≤ Sí. implicación f()Sí.≤ f()x),

para todo x e y en su dominio.

Una función constante es tanto monótona como antítona; por el contrario, si f es monótono y antítono, y si el dominio de f es una red, entonces f debe ser constante.

Las funciones monótonas son centrales en la teoría del orden. Aparecen en la mayoría de los artículos sobre el tema y en estos lugares se encuentran ejemplos de aplicaciones especiales. Algunas funciones monótonas especiales notables son incrustaciones de orden (funciones para las cuales x ≤ y si y solo si f(x) ≤ f(y)) e isomorfismos de orden (incrustaciones de orden sobreyectivo).

En los algoritmos de búsqueda

En el contexto de los algoritmos de búsqueda, la monotonicidad (también llamada coherencia) es una condición que se aplica a las funciones heurísticas. Una heurística h(n) es monótona si, para cada nodo n y cada sucesor n' de n generado por cualquier acción a, el costo estimado de alcanzar la meta desde n no es mayor que el costo del paso para llegar a n' más el costo estimado de alcanzar la meta desde n' ,

h()n)≤ ≤ c()n,a,n.)+h()n.).{displaystyle h(n)leq cleft(n,a,n'right)+hleft(n'right). }

Esta es una forma de desigualdad triangular, con n, n', y el objetivo G_n más cercano a n. Debido a que toda heurística monotónica también es admisible, la monotonicidad es un requisito más estricto que la admisibilidad. Algunos algoritmos heurísticos como A* pueden resultar óptimos siempre que la heurística que utilicen sea monótona.

En funciones booleanas

Con la función no monotónica "si a entonces ambos b y c" falso nodos aparecen arriba verdadero nodos.

Diagrama de Hasse de la función monotónica "al menos dos de a, b, c Espera". Los colores indican los valores de salida de la función.

En álgebra booleana, una función monótona es aquella que para todo a_i y b<sub i en {0,1}, si a₁ ≤ b ₁, a₂ ≤ b ₂,..., a_n ≤ b_n (es decir, el producto cartesiano {0, 1}ⁿ está ordenado por coordenadas), entonces f(a₁,..., a_n) ≤ f(b₁,..., b _n). En otras palabras, una función booleana es monótona si, para cada combinación de entradas, cambiar una de las entradas de falso a verdadero solo puede hacer que la salida cambie de falso a verdadero y no de verdadero a falso. Gráficamente, esto significa que una función booleana n-aria es monótona cuando su representación como un cubo n etiquetado con valores de verdad no tiene un borde ascendente de verdadero a falso . (Este diagrama de Hasse etiquetado es el dual del diagrama de Venn etiquetado de la función, que es la representación más común para n ≤ 3).

Las funciones booleanas monótonas son precisamente aquellas que se pueden definir mediante una expresión que combina las entradas (que pueden aparecer más de una vez) utilizando únicamente los operadores y y o (en particular no está prohibido). Por ejemplo, "al menos dos de a, b, c se mantienen" es una función monótona de a, b, c, ya que se puede escribir por ejemplo como ((a y b) o (a y c) o (b y c)).

El número de tales funciones en n variables se conoce como el número de Dedekind de n.