Funcion exponencial

Funciones exponenciales con bases 2 y 1/2

El función exponencial es una función matemática denotada por ${displaystyle f(x)=exp(x)}$ o ${displaystyle e^{x}$ (donde el argumento x está escrito como exponente). A menos que se especifique lo contrario, el término generalmente se refiere a la función de valor positivo de una variable real, aunque puede extenderse a los números complejos o generalizado a otros objetos matemáticos como matrices o álgebras Lie. La función exponencial se originó de la noción de exponenciación (multiplicación repetida), pero las definiciones modernas (hay varias caracterizaciones equivalentes) permiten que se extienda rigurosamente a todos los argumentos reales, incluyendo números irracionales. Su ocurrencia omnipresente en matemáticas puras y aplicadas llevó al matemático Walter Rudin a opine que la función exponencial es "la función más importante en las matemáticas".

La función exponencial satisface la identidad de exponenciación

$${displaystyle e^{x+y}=e^{x}e^{y}{text{ for all }x,yin mathbb {R}$$

${displaystyle e=exp(1)}$

${displaystyle e^{n}=underbrace {etimes cdots times e} _{n{text{ factors}}}}$

${displaystyle e=exp(1)}$

Mientras que otras funciones no feroces continuas ${displaystyle f:mathbb {R} to mathbb {R}$ que satisfacen la identidad de la exponentiación también se conoce como funciones exponenciales, la función exponencial exp es la función única de valor real de una variable real cuyo derivado es en sí mismo y cuyo valor a 0 es 1; es decir, ${displaystyle exp '(x)=exp(x)}$ para siempre real x, y ${displaystyle exp(0)=1.}$ Así, exp a veces se llama la función exponencial natural para distinguirlo de estas otras funciones exponenciales, que son las funciones de la forma ${displaystyle f(x)=ab^{x}$ donde la base b es un número real positivo. La relación ${displaystyle b^{x}=e^{xln B}$ positiva b real o complejo x establece una fuerte relación entre estas funciones, que explica esta terminología ambigua.

La función exponencial real también se puede definir como una serie de potencia. Esta definición de la serie de potencia se extiende fácilmente a argumentos complejos para permitir la función exponencial compleja ${displaystyle exp:mathbb {C} to mathbb {C}$ a definir. La compleja función exponencial tiene todos los valores complejos excepto para 0 y está estrechamente relacionada con las complejas funciones trigonométricas, como muestra la fórmula de Euler.

Motivado por propiedades más abstractas y caracterizaciones de la función exponencial, el exponencial se puede generalizar y definir para tipos completamente diferentes de objetos matemáticos (por ejemplo, una matriz cuadrada o un álgebra de Lie).

En entornos aplicados, las funciones exponenciales modelan una relación en la que un cambio constante en la variable independiente da el mismo cambio proporcional (es decir, un aumento o disminución porcentual) en la variable dependiente. Esto ocurre ampliamente en las ciencias naturales y sociales, como en una población que se reproduce a sí misma, un fondo que genera intereses compuestos o un cuerpo creciente de expertos en fabricación. Por lo tanto, la función exponencial también aparece en una variedad de contextos dentro de la física, la informática, la química, la ingeniería, la biología matemática y la economía.

La función exponencial real es una bijeción de ${displaystyle mathbb {R}$ a ${displaystyle (0;infty)}$. Su función inversa es el logaritmo natural, denotado ${displaystyle ln}$ ${displaystyle log}$ o ${displaystyle log _{e};}$ debido a esto, algunos textos antiguos se refieren a la función exponencial como antilogarithm.

Gráfico

El gráfico de ${displaystyle y=e^{x}$ es hacia arriba, y aumenta más rápido como x aumenta. El gráfico siempre está por encima del x-eje, pero se acerca arbitrariamente a él para grandes negativos x; así, el x-Eje es un asintoto horizontal. La ecuación ${displaystyle {tfrac {dx}e^{x}=e^{x}$ significa que la pendiente del tangente al gráfico en cada punto es igual a su Sí.- coordinado en ese momento.

Relación con funciones exponenciales más generales

La función exponencial ${displaystyle f(x)=e^{x}$ a veces se llama función exponencial natural para distinguirlo de las otras funciones exponenciales. El estudio de cualquier función exponencial se puede reducir fácilmente a la de la función exponencial natural, ya que por definición, para positivo b,

$${displaystyle ab^{x}:=ae^{xln B}$$

Como funciones de una variable real, las funciones exponenciales se caracterizan únicamente por el hecho de que la derivada de tal función es directamente proporcional al valor de la función. La constante de proporcionalidad de esta relación es el logaritmo natural de la base b:

$${displaystyle {frac {dx}b^{x} {fnMicrosoft} {fnMicrosoft}}} {fnK}ln(b)}=e^{xln(b)}=e^{xln(b)}ln(b)=b^{x}ln(b). }$$

Para b ■ 1, la función ${displaystyle b^{x}$ está aumentando (como se describe para b = e y b = 2), porque ${displaystyle ln b confiar0}$ hace que el derivado siempre positivo; mientras que para b 1, la función está disminuyendo (como se describe para b = 1/2); y b = 1 la función es constante.

Número de Euler e = 2.71828... es la base única para la cual la constante de proporcionalidad es 1, ya ${displaystyle ln(e)=1}$, por lo que la función es su propio derivado:

$${displaystyle {frac {dx}e^{x}=e^{x}ln(e)=e^{x}$$

Esta función también denotó como exp x, se llama la "función exponencial natural", o simplemente "la función exponencial". Puesto que cualquier función exponencial puede ser escrita en términos del exponencial natural como ${displaystyle b^{x}=e^{xln B}$, es computacional y conceptualmente conveniente reducir el estudio de funciones exponenciales a este particular. El exponencial natural es denotado por

$${displaystyle xmapsto e^{x}$$

$${displaystyle xmapsto exp x.}$$

La primera notación se usa comúnmente para exponentes más simples, mientras que la última se prefiere cuando el exponente es una expresión complicada.

Para números reales c y d, una función de la forma ${displaystyle f(x)=ab^{cx+d}$ es también una función exponencial, ya que puede ser reescrito como

$${displaystyle ab^{cx+d}=left(ab^{d}right)left(b^{c}right)^{x}$$

Definición formal

La función exponencial (en azul), y la suma de la primera n + 1 términos de su serie de energía (en rojo).

La función exponencial real ${displaystyle exp colon mathbb {R} to mathbb {R}$ se puede caracterizar de una variedad de maneras equivalentes. Es comúnmente definido por la siguiente serie de potencia:

$${displaystyle exp x:=sum _{k=0}{infty }{frac {x^{k} {k}}=1+x+{frac {x^{2}{2}+{frac} {x^{3}{6}+{frac} {x^{4}{24}+cdots$$

Puesto que el radio de convergencia de esta serie de energía es infinita, esta definición es, de hecho, aplicable a todos los números complejos ${displaystyle zin mathbb {C}$ (ver § Complejo plano para la extensión de ${displaystyle exp x}$ al plano complejo). La constante e puede ser definido como ${textstyle e=exp 1=sum _{k=0}{infty }(1/k!).}$

La diferenciación término a término de esta serie de energía revela que ${textstyle {frac {dx}exp x=exp x}$ para siempre real x, que conduce a otra caracterización común ${displaystyle exp x}$ como la solución única de la ecuación diferencial

$${displaystyle y'(x)=y(x),}$$

${displaystyle y(0)=1.}$

Basado en esta caracterización, la regla de cadena muestra que su función inversa, el logaritmo natural, satisfies ${textstyle {frac {d}{y}log - Sí.$ para ${displaystyle y título0,}$ o ${textstyle log - Sí. ¿Qué?.$ Esta relación conduce a una definición menos común de la función exponencial real ${displaystyle exp x}$ como solución ${displaystyle y}$ a la ecuación

$${displaystyle x=int ¿Qué? {1}},dt.}$$

Por medio del teorema del binomio y la definición de la serie de potencias, la función exponencial también se puede definir como el siguiente límite:

$${displaystyle exp x=lim _{ntoinfty }left(1+{frac {x}{n}right)}{n}}$$

Se puede demostrar que cada solución continua y no cero de la ecuación funcional ${displaystyle f(x+y)=f(x)f(y)}$ es una función exponencial, ${displaystyle f:mathbb {R} to mathbb {R} xmapsto e^{kx}$ con ${displaystyle kin mathbb {R}.}$

Resumen

La curva roja es la función exponencial. Las líneas horizontales negras muestran donde cruza las líneas verticales verdes.

La función exponencial surge siempre que una cantidad crece o decae a una tasa proporcional a su valor actual. Una de esas situaciones es el interés compuesto continuo y, de hecho, fue esta observación la que llevó a Jacob Bernoulli en 1683 al número

$${displaystyle lim _{ntoinfty }left(1+{frac {1}{n}right)^{n}}$$

Si un monto de capital de 1 gana intereses a una tasa anual de x compuesta mensualmente, entonces el interés ganado cada mes es x/< /span>12 veces el valor actual, por lo que cada mes el valor total se multiplica por (1 + < span role="math" class="fracción">x/12), y el valor al final del año es (1 + x/12 )¹². Si, en cambio, el interés se capitaliza diariamente, se convierte en (1 + x /365)³⁶⁵. Dejando que el número de intervalos de tiempo por año crezca sin límite conduce a la definición límite de la función exponencial,

$${displaystyle exp x=lim _{nto infty }left(1+{frac {x}{n}right)}{n}}} {n}}}$$

A partir de cualquiera de estas definiciones se puede demostrar que la función exponencial obedece a la identidad de exponenciación básica,

$${displaystyle exp(x+y)=exp xcdot exp y}$$

La derivada (tasa de cambio) de la función exponencial es la propia función exponencial. En términos más generales, una función con una tasa de cambio proporcional a la función misma (en lugar de igual a ella) se puede expresar en términos de la función exponencial. Esta propiedad de la función conduce al crecimiento exponencial o al decaimiento exponencial.

La función exponencial se extiende a toda una función en el plano complejo. La fórmula de Euler relaciona sus valores en argumentos puramente imaginarios con funciones trigonométricas. La función exponencial también tiene análogos para los que el argumento es una matriz, o incluso un elemento de un álgebra de Banach o un álgebra de Lie.

Derivadas y ecuaciones diferenciales

El derivado de la función exponencial es igual al valor de la función. Desde cualquier punto P en la curva (azul), dejar una línea tangente (rojo), y una línea vertical (verde) con altura h ser dibujado, formando un triángulo derecho con una base b sobre x-Eje. Desde la pendiente de la línea roja tangente (el derivado) en P es igual a la relación de la altura del triángulo con la base del triángulo (rise sobre la ejecución), y el derivado es igual al valor de la función, h debe ser igual a la proporción h a b. Por lo tanto, la base b debe ser siempre 1.

La importancia de la función exponencial en matemáticas y ciencias radica principalmente en su propiedad como la única función que es igual a su derivada y es igual a 1 cuando x = 0. Es decir,

$${displaystyle {frac {dx}e^{x}=e^{x}quad {text{y}quad}quad E^{0}=1.$$

Funciones de la forma ce^x para constantes c son las únicas funciones que son iguales a su derivada (por el teorema de Picard-Lindelöf). Otras formas de decir lo mismo incluyen:

• La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
• La tasa de aumento de la función a x es igual al valor de la función en x.
• La función resuelve la ecuación diferencial Sí.′ = Sí..
• exp es un punto fijo de derivación como funcional.

Si la tasa de crecimiento o decaimiento de una variable es proporcional a su tamaño, como es el caso del crecimiento ilimitado de la población (ver la catástrofe de Malthus), el interés compuesto continuo o el decaimiento radiactivo, entonces la variable se puede escribir como una tiempos constantes una función exponencial del tiempo. Explícitamente para cualquier constante real k, una función f: R< /b> → R satisface f′ = kf si y solo si f(x) = ce^kx para alguna constante c. La constante k se denomina constante de descomposición, constante de desintegración, constante de velocidad o constante de transformación< /b>.

Además, para cualquier función diferenciable f, encontramos, por la regla de la cadena:

$${displaystyle {frac {dx}e^{f(x)}=f'(x)e^{f(x)}.}$$

Fracciones continuas para ex

Se puede obtener una fracción continua para e^x a través de una identidad de Euler:

$${displaystyle e^{x}=1+{cfrac {x}{1-{cfrac {x}{x+2-{cfrac {2x}{x+3-{cfrac {3x}{x+4-ddots - Sí.$$

La siguiente fracción continua generalizada para e^z converge más rápidamente:

$${displaystyle e^{z}=1+{cfrac {2z}{2-z+{cfrac {2}{6+{frac} {fnK}{10+{fncipa} {Z^{2}{14+ddots - Sí.$$

o, aplicando la sustitución z = x/y< /lapso>:

$${displaystyle e^{frac {x}{y}=1+{2x}{2y-x+{cfrac {x^{2}{6y+{cfrac {x^{2}{10y+{cfrac {x^{2}{14y+ddots - Sí.$$

z = 2

$${displaystyle e^{2}=1+{cfrac {4}{0+{cfrac {2}{6+{cfrac {2}{2}{10+{cfrac {2}{14+ddots {fnMicrosoft Sans Serif}}}=7+{frac {2}{5+{cfrac {1}{7+{cfrac {1}{9+{cfrac {1}}}}$$

Esta fórmula también converge, aunque más lentamente, para z > 2. Por ejemplo:

$${displaystyle e^{3}=1+{cfrac {6}{-1+{cfrac {3^{2}{6+{cfrac {3^{2}{10+{cfrac {3^{2}{14+ddots {fnMicrosoft Sans Serif}}}=13+{frac {54}{7+{cfrac {9}{14+{cfrac {9}{18+{cfrac {9}}}}$$

Plano complejo

La función exponencial e^z trazado en el plano complejo de -2-2i a 2+2i

Una parcela compleja ${displaystyle zmapsto exp z}$, con el argumento ${displaystyle operatorname {Arg} exp z}$ representado por diferentes colores. La transición de colores oscuros a luz muestra que ${displaystyle left WordPressexp zright privacy}$ está aumentando sólo a la derecha. Las bandas horizontales periódicas correspondientes al mismo hue indican que ${displaystyle zmapsto exp z}$ es periódica en la parte imaginaria ${displaystyle z}$.

Como en el caso real, la función exponencial se puede definir en el plano complejo en varias formas equivalentes. La definición más común de la función exponencial compleja es paralela a la definición de serie de potencias para argumentos reales, donde la variable real se reemplaza por una compleja:

$${displaystyle exp z:=sum _{k=0}{infty }{frac !$$

Alternativamente, la función exponencial compleja puede definirse modelando la definición de límite para argumentos reales, pero reemplazando la variable real por una compleja:

$${displaystyle exp z:=lim _{nto infty }left(1+{frac {z}{n}right)}{n}}} {n}}$$

Para la definición de serie de potencias, la multiplicación por términos de dos copias de esta serie de potencias en el sentido de Cauchy, permitida por Mertens' teorema, muestra que la propiedad multiplicativa definitoria de las funciones exponenciales sigue siendo válida para todos los argumentos complejos:

$${displaystyle exp(w+z)=exp wexp z{text{ for all }w,zin mathbb {C}$$

La definición de la función exponencial compleja a su vez conduce a las definiciones apropiadas que extienden las funciones trigonométricas a argumentos complejos.

En particular, cuando z = it (t real), la definición de la serie produce la expansión

$${displaystyle exp(it)=left(1-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK} {4}} {fnMicroc} {t^{6}{6}}}+cdots right)+ileft(t-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK} {5}} {fnMicroc} {t^{7}{7}}+cdots right).}$$

En esta expansión, el reordenamiento de los términos en partes reales e imaginarias se justifica por la convergencia absoluta de la serie. Las partes real e imaginaria de la expresión anterior corresponden, de hecho, a las expansiones en serie de cos t y sin t, respectivamente.

Esta correspondencia proporciona motivación para Definición cosine y sine para todos los argumentos complejos en términos de ${displaystyle exp(pm iz)}$ y la serie de potencia equivalente:

$${displaystyle {begin{aligned} {cos z:={frac {exp(iz)+exp(-iz)}{2}=sum ¿Qué? {2K}{(2k)}}},\[5pt]{y }quadsin z:={frac {exp(iz)-exp(-iz)}{2i}=sum ¿Qué? {Z^{2k+1}{(2k+1)}}end{aligned}}} {cH00}} {cH00}}$$

para todos ${textstyle zin mathbb {C}$

Funciones exp, #, y pecado así definidos tienen radio infinito de convergencia por la prueba de ratio y son por lo tanto funciones enteras (es decir, holomorfo en ${displaystyle mathbb {C}$). El rango de la función exponencial es ${displaystyle mathbb {C} setminus {0}$, mientras que los rangos de las funciones sine compleja y cosina son ambos ${displaystyle mathbb {C}$ en su totalidad, de acuerdo con el teorema de Picard, que afirma que el rango de una función entera no constante es cualquiera de ${displaystyle mathbb {C}$, o ${displaystyle mathbb {C}$ excluyendo un valor lacunario.

Estas definiciones de las funciones exponencial y trigonométrica conducen trivialmente a la fórmula de Euler:

$${displaystyle exp(iz)=cos z+isin z{text{ for all }zin mathbb {C}$$

Alternativamente, podríamos definir la función exponencial compleja basada en esta relación. Si z = x + iy, donde x y y son reales, entonces podríamos definir su exponencial como

$${displaystyle exp z=exp(x+iy):=(exp x)(cos y+isin y)}$$

exp#pecado

Para ${displaystyle tin mathbb {R}$, la relación ${displaystyle {overline {exp(it)}=exp(-it)}$ sostiene, para que ${displaystyle left durableexp(it)right sobrevivir=1}$ de verdad ${displaystyle t}$ y ${displaystyle tmapsto exp(it)}$ mapas de la línea real (mod 2π) al círculo de la unidad en el plano complejo. Además, pasando de ${displaystyle t=0}$ a ${displaystyle t=t_{0}$, la curva definida ${displaystyle gamma (t)=exp(it)}$ traza un segmento del círculo de la unidad de la longitud

$${displaystyle int _{0}{t_{0}Sobrevivirgamma '(t) ¿Qué?$$

z = 1

La compleja función exponencial es periódica con el período 2πi y ${displaystyle exp(z+2pi ik)=exp z}$ para todos ${displaystyle zin mathbb {C}kin mathbb {Z}$.

Cuando su dominio se extiende desde la línea real hasta el plano complejo, la función exponencial conserva las siguientes propiedades:

$${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnK} {fnMicrosoft ]} {fnKf} {fnMicrosoft} {f}} {f}f} {f}f}f}f}f}f}f}fnKf}fnKf}f}fnKfnKfnKfnKf}fnKf}fnKfnKfnKfnKfnKfnKf}f}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}f}fn$$

para todos ${textstyle w,zin mathbb {C}$

La extensión del logaritmo natural a argumentos complejos produce el logaritmo complejo log z, que es una función multivaluada.

Entonces podemos definir una exponenciación más general:

$${displaystyle z^{w}=e^{wlog z}$$

zwzlog zz^wz

()e^z)^w
ل e^zw, pero más bien ()e^z)^w
= e^{()z + 2niego)w} multivalorado sobre enteros n

Consulte falla de identidades de potencia y logaritmo para obtener más información sobre los problemas con la combinación de potencias.

La función exponencial asigna cualquier línea en el plano complejo a una espiral logarítmica en el plano complejo con el centro en el origen. Existen dos casos especiales: cuando la línea original es paralela al eje real, la espiral resultante nunca se cierra sobre sí misma; cuando la línea original es paralela al eje imaginario, la espiral resultante es un círculo de cierto radio.

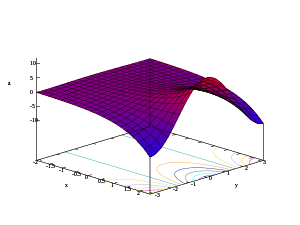
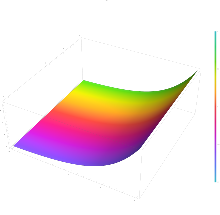
• Parcelas 3D de parte real, parte imaginaria y módulo de la función exponencial
• 

  z = Re(e^{x + i})

• 

  z = Im(e^{x + i})

• 

  z = Silencioe^{x + i}Silencio

Considerando la función exponencial compleja como una función que involucra cuatro variables reales:

$${displaystyle v+iw=exp(x+iy)}$$

Comenzando con una porción codificada en color de la ${displaystyle xy}$ dominio, los siguientes son representaciones del gráfico como varias proyectadas en dos o tres dimensiones.

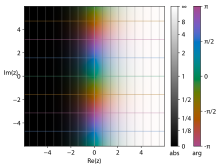
• Gráficos de la función exponencial compleja
• 

  Llave de tablero:
  ${displaystyle x confianza0:;{text{green}}$
  ${displaystyle x won0:;{text{red}}$
  ${displaystyle y confía0:;{text{yellow}}$
  ${displaystyle y made0:;{text{blue}}$

• 

  Proyección sobre el plano complejo de rango (V/W). Compare con el siguiente cuadro de perspectiva.

• 

  Proyección en la ${displaystyle x}$, ${displaystyle v}$, y ${displaystyle w}$ Dimensiones, produciendo un cuerno o forma de embudo (imagen de perspectiva 2-D).

• 

  Proyección en la ${displaystyle y}$, ${displaystyle v}$, y ${displaystyle w}$ dimensiones, produciendo una forma espiral. ()${displaystyle y}$ rango extendido a ±2π, de nuevo como imagen de perspectiva 2-D).

La segunda imagen muestra cómo el plano complejo de dominio se asigna al plano complejo de rango:

• cero se asigna a 1
• lo real ${displaystyle x}$ axis se asigna al real positivo ${displaystyle v}$ axis
• el imaginario ${displaystyle y}$ el eje está envuelto alrededor del círculo de la unidad a una velocidad angular constante
• valores con partes reales negativas se mapean dentro del círculo de unidad
• valores con partes reales positivas se mapean fuera del círculo de la unidad
• valores con una parte real constante se mapean a círculos centrados en cero
• valores con una parte imaginaria constante se mapean a los rayos que se extienden desde cero

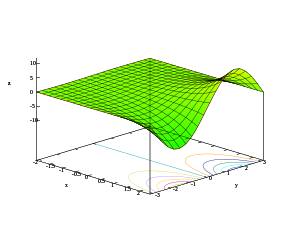
Las imágenes tercera y cuarta muestran cómo el gráfico de la segunda imagen se extiende a una de las otras dos dimensiones que no se muestran en la segunda imagen.

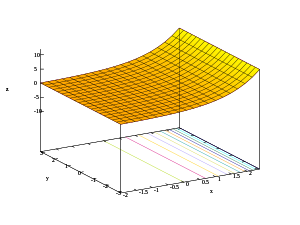
La tercera imagen muestra el gráfico extendido a lo largo del real ${displaystyle x}$ Axis. Muestra que el gráfico es una superficie de revolución sobre la ${displaystyle x}$ eje del gráfico de la función exponencial real, produciendo una forma de cuerno o embudo.

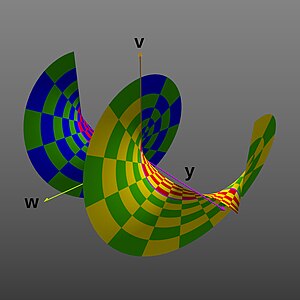
La cuarta imagen muestra el gráfico extendido a lo largo del imaginario ${displaystyle y}$ Axis. Muestra que la superficie del gráfico para positivo y negativo ${displaystyle y}$ los valores realmente no se encuentran a lo largo del real negativo ${displaystyle v}$ axis, pero en cambio forma una superficie espiral sobre el ${displaystyle y}$ Axis. Porque es ${displaystyle y}$ valores se han ampliado ±2π, esta imagen también representa mejor la periodicidad 2π en el imaginario ${displaystyle y}$ valor.

Cálculo de ab donde tanto a como b son complejos

La exponenciación compleja a^b se puede definir convirtiendo a a coordenadas polares y usando la identidad (e^{ln a})^b
= a^b< /lapso>:

$${displaystyle a^{b}=left(re^{theta i}right)^{b}=left(e^{(ln r)+theta i}right)}{b}=e^{left(ln r)+theta iright)b}}}}$$

Sin embargo, cuando b no es un número entero, esta función tiene varios valores, porque θ< /i> no es único (ver falla de poder e identidades logarítmicas).

Matrices y álgebras de Banach

La definición de serie de potencias de la función exponencial tiene sentido para matrices cuadradas (para las cuales la función se llama matriz exponencial) y más generalmente en cualquier álgebra unitaria de Banach B. En esta configuración, e⁰ = 1 y e^x es invertible con inversa e^{−x< /i>} para cualquier x en B . Si xy = yx, entonces e^x + y = e^xe ^y, pero esta identidad puede fallar para no viajar x y y.

Algunas definiciones alternativas conducen a la misma función. Por ejemplo, e^x se puede definir como

$${displaystyle lim _{nto infty }left(1+{frac {x}{n}right)^{n}$$

O e^x se puede definir como f_x(1), donde f< sub>x: R → B es la solución a la ecuación diferencial df_x/dt(t) = x f_x(t), con condición inicial f_x(0) = 1; se deduce que f_x(t) = e< /i>^tx para cada t en < abarcan clase="texhtml">R.

Álgebras de mentira

Dado un grupo de Lie G y sus asociados Lie algebra ${displaystyle {Mathfrak {}}$, el mapa exponencial es un mapa ${displaystyle {Mathfrak {}}$ ↦ G satisfaciendo propiedades similares. De hecho, desde R es el álgebra Lie del grupo Lie de todos los números reales positivos bajo la multiplicación, la función exponencial ordinaria para los argumentos reales es un caso especial de la situación del álgebra Lie. Del mismo modo, desde el grupo Lie GL(n,R) of invertible n × n matrices tiene como Álgebra de Lie M(n,R), el espacio de todos n × n matrices, la función exponencial para matrices cuadradas es un caso especial del mapa exponencial del álgebra Lie.

La identidad exp(x + y) = exp x exp y puede fallar para los elementos de álgebra de Lie x y y< /span> que no viajan; la fórmula de Baker-Campbell-Hausdorff proporciona los términos de corrección necesarios.

Trascendencia

La función e^z no está en C(z) (es decir, no es el cociente de dos polinomios con coeficientes complejos).

Si a₁,..., a_n son números complejos distintos, entonces e^a₁z,..., e^a_nz son linealmente independientes sobre C(z). De ello se deduce que e^z es trascendental sobre < b>C(z).

Cálculo

Al calcular (una aproximación de) la función exponencial cerca del argumento 0, el resultado será cerca de 1, y computar el valor de la diferencia ${displaystyle e^{x}-1}$ con aritmética de punto flotante puede llevar a la pérdida de (posiblemente todas) cifras significativas, produciendo un gran error de cálculo, posiblemente incluso un resultado sin sentido.

Siguiendo una propuesta de William Kahan, puede ser útil tener una rutina dedicada, a menudo llamada expm1, para calcular e^x − 1 directamente, omitiendo el cálculo de e^x . Por ejemplo, si la exponencial se calcula utilizando su serie de Taylor

$${displaystyle e^{x}=1+x+{frac {x^{2}{2}+{frac} {x^{3}{6}+cdots ¡No!$$

${displaystyle e^{x}-1}$

$${displaystyle e^{x}-1=x+{frac {x^{2}{2}+{frac} {x^{3}{6}+cdots ¡No!$$

Esto se implementó por primera vez en 1979 en la calculadora Hewlett-Packard HP-41C y lo proporcionaron varias calculadoras, sistemas operativos (por ejemplo, Berkeley UNIX 4.3BSD), sistemas de álgebra informática y lenguajes de programación (por ejemplo, C99).

Además de la base e, el estándar IEEE 754-2008 define funciones exponenciales similares cerca de 0 para base 2 y 10: ${displaystyle 2^{x}-1}$ y ${displaystyle 10^{x}-1}$.

Se ha utilizado un enfoque similar para el logaritmo (ver lnp1).

Una identidad en términos de la tangente hiperbólica,

$${displaystyle operatorname {expm1} (x)=e^{x}-1={frac {2tanh(x/2)}{1-tanh(x/2)}}}}$$

xexpm1(x)

Alternativamente, se puede usar esta expresión:

${displaystyle e^{x}-1=lim _{nto infty }{frac {x}{n}sum ¿Por qué?$