Función de distribución empírica

La curva verde, que aborda asintomáticamente las alturas de 0 y 1 sin alcanzarlas, es la verdadera función de distribución acumulativa de la distribución normal estándar. Las marcas de hash gris representan las observaciones en una muestra particular extraída de esa distribución, y los pasos horizontales de la función de paso azul (incluyendo el punto más izquierdo en cada paso pero no incluyendo el punto más derecho) forman la función de distribución empírica de esa muestra. ()Haga clic aquí para cargar un nuevo gráfico.)

En estadística, una función de distribución empírica (comúnmente también llamada función de distribución acumulativa empírica, eCDF) es la función de distribución asociada con la medida empírica de una muestra. Esta función de distribución acumulativa es una función escalonada que salta 1/n en cada uno de los n. puntos de datos. Su valor en cualquier valor especificado de la variable medida es la fracción de observaciones de la variable medida que son menores o iguales al valor especificado.

La función de distribución empírica es una estimación de la función de distribución acumulativa que generó los puntos en la muestra. Converge con probabilidad 1 a esa distribución subyacente, según el teorema de Glivenko-Cantelli. Existen varios resultados para cuantificar la tasa de convergencia de la función de distribución empírica con la función de distribución acumulativa subyacente.

Definición

Sea (X₁, …, X_n</i ) ser variables aleatorias reales independientes y distribuidas de forma idéntica con la función de distribución acumulativa común F(t) . Entonces la función de distribución empírica se define como

F^ ^ n()t)=Número de elementos en la muestra≤ ≤ tn=1n. . i=1n1Xi≤ ≤ t,{displaystyle {widehat {F}_{n}(t)={frac {mbox{number of elements in the sample}leq {fn}= {fn} {fn}} {fn}} {fn} {fn}} {fn}}} {fn}}} {fn}}} {fn}} {fn}}}}} {fn}}} {fn} {fn} {fn}}} {f}}}}}} {f}}}}}}}}}} {f}}}}}}} {f}}}}}}}}}}}} {f} {f} {fn}}}}}}}}}}}}}}}}} {f} {f} {f} {fn}}} {fn}} {fn}} {f} {fn}}f}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}f}}}}}}}}}} ¿Qué? {1} _{X_{i}leq t}

Donde 1A{displaystyle mathbf {1} es el indicador del evento A. Para un fijo t, el indicador 1Xi≤ ≤ t{displaystyle mathbf {1} _{X_{i}leq t} es una variable aleatoria Bernoulli con parámetro p = F()t); por lo tanto nF^ ^ n()t){fnMicrosoft Sans Serif} {fn} {fn}} {fn} {fn}} {fn} {fn} {fn}}} {fn}} {fn}} {fn}} {fn}} {fn}}}}}}}}}}} {fn}}}}}}} es una variable binomial aleatoria con media nF()t) y diferencia nF()t)(1 - F()t). Esto implica que F^ ^ n()t){displaystyle {widehat {F}_{n}(t)} es un estimador imparcial para F()t).

Sin embargo, en algunos libros de texto, la definición se da como

F^ ^ n()t)=1n+1. . i=1n1Xi≤ ≤ t{displaystyle {widehat {f} {fn} {fn}}}sum} {fn}}} {fn}} {fn}} {fn}}} {fn}}}}} {fn0}}}}}} {fn} {fn} {fn} {fn}fn}}}}}}}fn}}}}}}}}}}}f}}}}}}}}}}}}}}}}}fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}} {f} {fn} {fn} {fn}} {fn}fn}}fn}}}fn}f}}}}}}}}}}}}}fn}}}}}fn} {fn}fn}}fn}} ¿Qué? {1} _{X_{i}leq t}

Propiedades asintóticas

Dado que la relación (n + 1)/n se acerca a 1 cuando n va al infinito, las propiedades asintóticas de las dos definiciones dadas anteriormente son las mismas.

Por la fuerte ley de grandes números, el estimador F^ ^ n()t){displaystyle scriptstyle {widehat {F}_{n}(t)} convergencias a F()t) como n→ casi seguro, por cada valor de t:

F^ ^ n()t) →a.s. F()t);{fnMicrosoft Sans Serif} {xrightarrow {text{a.s}} F(t);}

así el estimador F^ ^ n()t){displaystyle scriptstyle {widehat {F}_{n}(t)} es consistente. Esta expresión afirma la convergencia puntual de la función de distribución empírica a la verdadera función de distribución acumulativa. Hay un resultado más fuerte, llamado el teorema Glivenko-Cantelli, que afirma que la convergencia de hecho ocurre uniformemente sobre t:

. . F^ ^ n− − F. . JUEGO JUEGO ↑ ↑ Supt▪ ▪ RSilencioF^ ^ n()t)− − F()t)Silencio →a.s. 0.{displaystyle "Princesa" {F}_{n}-F infty }equiv sup _{tin mathbb {fn} {fn} {bign} {fn} {fn} {bign} {bign}}mxrightarrow {text{a.s}} 0.}

El sup-norm en esta expresión se llama la estadística Kolmogorov–Smirnov para probar la bondad de la adaptación entre la distribución empírica F^ ^ n()t){displaystyle scriptstyle {widehat {F}_{n}(t)} y la verdadera función de distribución acumulativa F. Otras funciones de la norma pueden utilizarse razonablemente aquí en lugar del sup-norm. Por ejemplo, el L2-norm da lugar a la estadística Cramér-von Mises.

La distribución asintotica se puede caracterizar de varias maneras diferentes. En primer lugar, el teorema del límite central establece que punto a punto, F^ ^ n()t){displaystyle scriptstyle {widehat {F}_{n}(t)} tiene distribución asintotically normal con el estándar n{displaystyle {sqrt {n}} tasa de convergencia:

n()F^ ^ n()t)− − F()t)) →d N()0,F()t)()1− − F()t))).{displaystyle {sqrt {}{big}{widehat {F}_{n}(t)-F(t){big)} {xrightarrow {d} {fnMitcal {fn} {Big}0,F(t){big (}1-F(t){big)}{Big)}}}

Este resultado es extendido por el teorema del Donsker, que afirma que empírico proceso n()F^ ^ n− − F){displaystyle scriptstyle {sqrt {n}({widehat) {F}_{n}-F)}, vista como una función indexada por t▪ ▪ R{displaystyle scriptstyle tin mathbb {R}, converge en la distribución en el espacio Skorokhod D[− − JUEGO JUEGO ,+JUEGO JUEGO ]{displaystyle scriptstyle D[-infty+infty]} al proceso medio-cero Gausiano GF=B∘ ∘ F{displaystyle scriptstyle G_{F}=Bcirc F}, donde B es el puente Brownian estándar. La estructura de covariancia de este proceso gausiano es

E⁡ ⁡ [GF()t1)GF()t2)]=F()t1∧ ∧ t2)− − F()t1)F()t2).{displaystyle operatorname {E} [,G_{F}(t_{1})G_{F}(t_{2}),]=F(t_{1}wedge t_{2})-F(t_{1})F(t_{2}). }

La tasa uniforme de convergencia en el teorema de Donsker se puede cuantificar mediante el resultado conocido como incrustación húngara:

<math alttext="{displaystyle limsup _{nto infty }{frac {sqrt {n}}{ln ^{2}n}}{big |}{sqrt {n}}({widehat {F}}_{n}-F)-G_{F,n}{big |}_{infty }lim supn→ → JUEGO JUEGO nIn2⁡ ⁡ n.n()F^ ^ n− − F)− − GF,n.JUEGO JUEGO c)JUEGO JUEGO ,a.s.{displaystyle limsup _{nto infty}{frac {sqrt {fn} {fn} {bigbigfn} {fn} {fn} {fn} {fn} {fn}} {fn}} {fn}} {fn} {fn}}} {fn} {fn}}} {fn}} {fn}}}}}}}} {f}}}}}}}}}}}} {n}}}}}}}} {\n}}} {n}}}}} {n}}} {n} {n}} {b}}}}}}}}}}}}}}}}}}}}} {n}}}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\n} {F}_{n}-F)-G_{F,n} {bigfn}_{inftyinftyquad {text{a.s}}<img alt="{displaystyle limsup _{nto infty }{frac {sqrt {n}}{ln ^{2}n}}{big |}{sqrt {n}}({widehat {F}}_{n}-F)-G_{F,n}{big |}_{infty }

Alternativamente, la tasa de convergencia de n()F^ ^ n− − F){displaystyle scriptstyle {sqrt {n}({widehat) {F}_{n}-F)} también se puede cuantificar en términos del comportamiento asintotico del sup-norm de esta expresión. Número de resultados existen en este lugar, por ejemplo, la desigualdad Dvoretzky–Kiefer–Wolfowitz proporciona límites a las probabilidades de cola n. . F^ ^ n− − F. . JUEGO JUEGO {displaystyle scriptstyle {sqrt {n}fn}fncipado {fnHFF} {fn}-Ffn}:

z{Big)}leq 2e^{-2z^{2}}.}" xmlns="http://www.w3.org/1998/Math/MathML">Pr()n. . F^ ^ n− − F. . JUEGO JUEGO ■z)≤ ≤ 2e− − 2z2.{displaystyle Pr !{Big (}{sqrt {n} {F}_ {fn}leq 2e^{2}}z{Big)}leq 2e^{-2z^{2}}.}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9a32e831e0665a67573a14d706f80fc48c6e8228" style="vertical-align: -1.838ex; width:34.584ex; height:4.843ex;"/>

De hecho, Kolmogorov ha demostrado que si la función de distribución acumulativa F es continua, entonces la expresión n. . F^ ^ n− − F. . JUEGO JUEGO {displaystyle scriptstyle {sqrt {n}fn}fncipado {fnHFF} {fn}-Ffn} convergencias en la distribución a . . B. . JUEGO JUEGO {displaystyle scriptstyle aboveBfnso_{infty}, que tiene la distribución de Kolmogorov que no depende de la forma de F.

Otro resultado, que se deriva de la ley del logaritmo iterado, es que

lim supn→ → JUEGO JUEGO n. . F^ ^ n− − F. . JUEGO JUEGO 2In⁡ ⁡ In⁡ ⁡ n≤ ≤ 12,a.s.{displaystyle limsup _{nto infty }{frac {fnh}fnh}fnh00fnh00fnh00fnh}fnfn}fn}fn\\fnH00\fnH00\fn\fnH00\\fnH00fn}fnH00}\\fn\fn\\fnfn\fn\\fnfnfn\fnfnfnfn\\fnH00fn\fn\\\fnHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH00}}fn}\\\\\fn}}}}}fn} {F}_ {fn}fnfnnfnnfnnn}}leq {frac {1}{2}}quad {text{a.s}}}}} {fnfnfnK}}}}

y

lim infn→ → JUEGO JUEGO 2nIn⁡ ⁡ In⁡ ⁡ n. . F^ ^ n− − F. . JUEGO JUEGO =π π 2,a.s.{displaystyle liminf _{nto infty }{sqrt {2nlnln ln "Antes" {F}_ {fn}-Ffnh00} {fnMicrosoft Sans Serif}

Intervalos de confianza

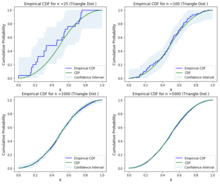
Según Dvoretzky–Kiefer–Wolfowitz desigualdad el intervalo que contiene el verdadero CDF, F()x){displaystyle F(x)}, con probabilidad 1− − α α {displaystyle 1-alpha } se especifica como

Fn()x)− − ε ε ≤ ≤ F()x)≤ ≤ Fn()x)+ε ε Donde ε ε =In⁡ ⁡ 2α α 2n.{displaystyle F_{n}(x)-varepsilon leq F(x)leq F_{n}(x)+varepsilon ;{text{ where }varepsilon {fnMicroc} {2}{alpha - Sí.

Según los límites anteriores, podemos trazar el CDF empírico, el CDF y los intervalos de confianza para diferentes distribuciones utilizando cualquiera de las implementaciones estadísticas.

Implementación estadística

Una lista no exhaustiva de implementaciones de software de la función de distribución empírica incluye:

• En el software R computamos una función de distribución acumulativa empírica, con varios métodos para trazar, imprimir y computar con tal objeto “ecdf”.
• En MATLAB podemos utilizar la función de distribución acumulativa empírica (cdf)
• jmp de SAS, la trama CDF crea una trama de la función de distribución acumulativa empírica.
• Minitab, crear un CDF empírico
• Mathwave, podemos ajustar la distribución de probabilidad a nuestros datos
• Dataplot, podemos trazar trama de CDF empírico
• Scipy, podemos usar scipy.stats.ecdf
• Statsmodels, podemos utilizar Estadísticasmodels.distributions.empirical_distribution.ECDF
• Matplotlib, utilizando la función matplotlib.pyplot.ecdf (nueva en la versión 3.8.0)
• Seaborn, usando el marino. función ecdfplot
• Plotly, usando la función plotly.express.ecdf
• Excel, podemos trazar la trama empírica de CDF
• ArviZ, utilizando la función az.plot_ecdf