Familias de soluciones a ecuaciones diferenciales relacionadas

Las funciones de Bessel son la parte radial de los modos de vibración de un cabezal circular.
Las funciones de Bessel, definidas primero por el matemático Daniel Bernoulli y luego generalizadas por Friedrich Bessel, son soluciones canónicas y( x) de la ecuación diferencial de Bessel
x2d2Sí.dx2+xdSí.dx+()x2− − α α 2)Sí.=0{displaystyle x^{2}{frac} {fnMicroc}fnMicroc {y} {dx}+left(x^{2}-alpha ^{2}right)y=0}

 ordenα α {displaystyle alpha }
ordenα α {displaystyle alpha } − − α α {displaystyle - Alpha.
− − α α {displaystyle - Alpha. α α {displaystyle alpha }
α α {displaystyle alpha }
Los casos más importantes son cuando α α {displaystyle alpha } es un entero o medio entero. Funciones de Bessel para entero α α {displaystyle alpha }
es un entero o medio entero. Funciones de Bessel para entero α α {displaystyle alpha } son también conocidos como Funciones del cilindro o el armónicos cilíndricos porque aparecen en la solución a la ecuación de Laplace en coordenadas cilíndricas. Funciones de Bessel Spherical con medio entero α α {displaystyle alpha }
son también conocidos como Funciones del cilindro o el armónicos cilíndricos porque aparecen en la solución a la ecuación de Laplace en coordenadas cilíndricas. Funciones de Bessel Spherical con medio entero α α {displaystyle alpha } se obtienen cuando la ecuación Helmholtz se resuelve en coordenadas esféricas.
se obtienen cuando la ecuación Helmholtz se resuelve en coordenadas esféricas.
Aplicaciones de las funciones de Bessel
La función de Bessel es una generalización de la función seno. Puede interpretarse como la vibración de una cuerda con espesor variable, tensión variable (o ambas condiciones simultáneamente); vibraciones en un medio con propiedades variables; vibraciones de la membrana del disco, etc.
La ecuación de Bessel surge al encontrar soluciones separables a la ecuación de Laplace y la ecuación de Helmholtz en coordenadas cilíndricas o esféricas. Por lo tanto, las funciones de Bessel son especialmente importantes para muchos problemas de propagación de ondas y potenciales estáticos. Al resolver problemas en sistemas de coordenadas cilíndricas, se obtienen funciones de Bessel de orden entero (α = n); en problemas esféricos, se obtienen órdenes semienteros (α = n + 1/2). Por ejemplo:
- Olas electromagnéticas en una guía de onda cilíndrica
- Ampliaciones de presión de flujos rotacionales invisidos
- Conducción de calor en un objeto cilíndrico
- Modos de vibración de una membrana acústica circular o anular delgada (como un cabezal de tambor u otro membranofono) o placas más gruesas como el metal de hoja (ver la teoría de la placa Kirchhoff–Love, Mindlin–Reissner)
- Problemas de derrame en una celosía
- Soluciones a la ecuación de Schrödinger radial (en coordenadas esféricas y cilíndricas) para una partícula libre
- Resolver patrones de radiación acústica
- Fricción dependiente de frecuencia en tuberías circulares
- Dinámica de los cuerpos flotantes
- Resolución angular
- Diffraction from helical objects, including DNA
- Función de densidad de probabilidad del producto de dos variables aleatorias normalmente distribuidas
- Analizar las ondas superficiales generadas por microtremors, en geofísica y sismología.
Las funciones de Bessel también aparecen en otros problemas, como el procesamiento de señales (por ejemplo, véase la síntesis de audio FM, la ventana de Kaiser o el filtro de Bessel).
Definiciones
Debido a que esta es una ecuación diferencial lineal de segundo orden, debe haber dos soluciones linealmente independientes. Sin embargo, dependiendo de las circunstancias, son convenientes varias formulaciones de estas soluciones. Las diferentes variaciones se resumen en la siguiente tabla y se describen en las siguientes secciones.
| Tipo | Primera clase | Segundo tipo
|
|---|
| Funciones de Bessel
| Jα | Yα |
| Funciones de Bessel modificadas
| Iα | Kα |
| Funciones de Hankel
| H1)
α = Jα + iα | H2)
α = Jα − iα |
| Funciones de Bessel Spherical
| jn | Sí.n |
| Funciones de Hankel esférico
| h1)
n = jn + in | h2)
n = jn − in |
Las funciones de Bessel de segundo tipo y las funciones de Bessel esféricas de segundo tipo a veces se indican con Nn y nn, respectivamente, en lugar de Yn y yn.
Funciones de Bessel de primera clase: Jα
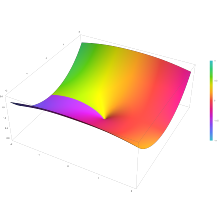
Parcela de la función Bessel del primer tipo
Jn()z) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

Plot of Bessel function of the first kind,
Jα()x), para pedidos enteros
α = 0, 1, 2Funciones de Bessel de primer tipo, indicadas como Jα(x), son soluciones de la ecuación diferencial de Bessel. Para números enteros o positivos α, las funciones de Bessel del primer tipo son finitas en el origen (x = 0); mientras que para números negativos no enteros α, las funciones de Bessel del primer tipo divergen como x tiende a cero. Es posible definir la función por su expansión en serie alrededor de x = 0, que se puede encontrar aplicando el método de Frobenius a Bessel's ecuación:
Jα α ()x)=.. m=0JUEGO JUEGO ()− − 1)mm!.. ()m+α α +1)()x2)2m+α α ,{displaystyle J_{alpha }(x)=sum _{m=0}{infty }{frac {(-1)^{m}{m}m! Gamma (m+alpha +1)} {left({frac {x}{2}right)}^{2m+alpha }}

 x−J1()x)J0()x)Sin x# xJn()x)Jn ± 1()x)
x−J1()x)J0()x)Sin x# xJn()x)Jn ± 1()x)Para α no enteros, las funciones Jα (x) y J−α(x) son linealmente independientes y, por lo tanto, son las dos soluciones de la ecuación diferencial. Por otro lado, para el orden de enteros n, la siguiente relación es válida (la función gamma tiene polos simples en cada uno de los no -enteros positivos):
J− − n()x)=()− − 1)nJn()x).{displaystyle J_{-n}(x)=(-1)^{n}J_{n}(x).}

Esto significa que las dos soluciones ya no son linealmente independientes. En este caso, se encuentra que la segunda solución linealmente independiente es la función de Bessel de segundo tipo, como se analiza a continuación.
Integrales de Bessel
Otra definición de la función de Bessel, para valores enteros de n, es posible usando una representación integral:
Jn()x)=1π π ∫ ∫ 0π π # ()nτ τ − − xpecado τ τ )dτ τ =12π π ∫ ∫ − − π π π π ei()nτ τ − − xpecado τ τ )dτ τ ,{displaystyle J_{n}(x)={frac {1}{pi }int _{0}^{pi }cos(ntau -xsin tau),dtau ={frac {1}{2pi) ########## {fntau -xsin tau},dtau}

Este fue el enfoque que usó Bessel, y de esta definición derivó varias propiedades de la función. La definición puede extenderse a órdenes no enteros mediante una de las integrales de Schläfli, para Re(x) > 0:
Jα α ()x)=1π π ∫ ∫ 0π π # ()α α τ τ − − xpecado τ τ )dτ τ − − pecado α α π π π π ∫ ∫ 0JUEGO JUEGO e− − xpecado t− − α α tdt.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}f}f}f}f}f}f}fone}f}f}f}f}f}f}f}f}f}f}fnKfnKf}f}f}f}f}f}fnKf}f}fnKf}fnKf}fnKfnMicrob9}fnKfnKfnKfnMinKfnKfnKf}fnKf}fnMin

Relación con series hipergeométricas
Las funciones de Bessel se pueden expresar en términos de la serie hipergeométrica generalizada como
Jα α ()x)=()x2)α α .. ()α α +1)0F1()α α +1;− − x24).{displaystyle J_{alpha }(x)={frac {left({frac {x}{2}}right)}{alpha {fnMicrosoft Sans Serif +1)};_{0}F_{1}left(alpha +1;-{frac {x^{2}{4}}right).}

Esta expresión está relacionada con el desarrollo de las funciones de Bessel en términos de la función de Bessel-Clifford.
Relación con los polinomios de Laguerre
En términos de los polinomios de Laguerre Lk y el parámetro elegido arbitrariamente t, la función de Bessel se puede expresar como
Jα α ()x)()x2)α α =e− − t.. ()α α +1).. k=0JUEGO JUEGO Lk()α α )()x24t)()k+α α k)tkk!.{displaystyle {frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}f}}}fnMicroc}}f}f}}f}f}f}f}}f}f}f}f}f}f}f}fnKf}fnKf}fnKf}fnMicrocf}fnKf}fnKf}fnKfnKfnMicrocfnMicroc}}fnMicrocH0}}fnMicroc}}fnMicroc}}fnMicroc}}}fn {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}} {f}}} {fnMicroc {f}}} {f}}}} {f}}}}}}}} {f}} {f}}} {f}}}}}}}}}}}}\\\\f}f}f}\f}f}f}f}\f}f}f}fnfnfnf}f}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnf}fnfn Gamma (alpha +1)}sum _{k=0}{infty }{frac {L_{k}{(alpha)}left({frac {x^{2}{4t}right)}{binom {k+alpha }{k} {frac {T} {k} {k}}}}

Funciones de Bessel de segunda especie: Yα
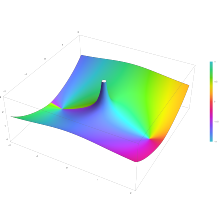
Parcela de la función Bessel del segundo tipo
Yn()z) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

Plot of Bessel function of the second kind,
Yα()x), para pedidos enteros
α = 0, 1, 2Las funciones de Bessel de segundo tipo, indicadas por Yα(x), ocasionalmente denotado por Nα(x), son soluciones de Bessel ecuación diferencial que tiene una singularidad en el origen (x = 0) y tiene varios valores. Estas a veces se denominan funciones de Weber, ya que fueron introducidas por H. M. Weber (1873), y también funciones de Neumann después de Carl Neumann.
Para α no enteros, Yα(x) está relacionado con Jα(x) por
Yα α ()x)=Jα α ()x)# ()α α π π )− − J− − α α ()x)pecado ()α α π π ).{displaystyle Y_{alpha }(x)={frac {J_{alpha }(x)cos(alpha pi)-J_{-alpha }(x)}{sin(alpha pi)}}}}}}

En el caso del orden de los enteros n, la función se define tomando el límite como una α tiende a n:
Yn()x)=limα α → → nYα α ()x).{displaystyle Y_{n}(x)=lim _{alpha to n}Y_{alpha }(x).}

Si n es un entero no negativo, tenemos la serie
Yn()z)=− − ()z2)− − nπ π .. k=0n− − 1()n− − k− − 1)!k!()z24)k+2π π Jn()z)In z2− − ()z2)nπ π .. k=0JUEGO JUEGO ()↑ ↑ ()k+1)+↑ ↑ ()n+k+1))()− − z24)kk!()n+k)!{displaystyle Y... {fnMicrosoft Sans Serif}}left({frac {fn-k-1)}}left({frac {frac] {fnMicroc} {fn} {fnMicroc} {fn} {fn} {fn} {fn} {fn} {fn}fn}fn}fnfnfnfn}fnfn}fnfnKfnK}fnKfn}fnKfn}fnKfn}fn}fn9}fn9}fnfnfnfnKfnKfnKfnKfn}fnKfnKfnKfn}fnKfn}fnKfn}fn}fn}fn}fn}fnKfnfn}fn}fn}fn}fnKfn}fnKfn}fn}fn}fn {fn} {fn}fn}} {fn}}} {fn} {fn}} {fn}} {fn}} {fn}}}}} {fn} {fn} {fn}} {fn}}}} {fn}fn}fn}}}}f}f}} {fn}}}}}}fn}}}}}fnfnfnf}f}f}fnfn}f}fnfnfnfnfnfnfnfn}fnfnfn}fnfn}fnfn}}}fnfn}fnfnfn}}fnfn}}fn}fnfnfnfn}}}fnfn}}}fn }sum _{k=0} {infty }(psi (k+1)+psi (n+k+1)){frac {left(-{frac ¡Sí!

Donde ↑ ↑ ()z){displaystyle psi (z)} es la función digamma, el derivado logarítmico de la función gamma.
es la función digamma, el derivado logarítmico de la función gamma.
También hay una fórmula integral correspondiente (para Re(x) > 0):
Yn()x)=1π π ∫ ∫ 0π π pecado ()xpecado Silencio Silencio − − nSilencio Silencio )dSilencio Silencio − − 1π π ∫ ∫ 0JUEGO JUEGO ()ent+()− − 1)ne− − nt)e− − xpecado tdt.{displaystyle Y_{n}(x)={frac {1}{pi }int _{0}pi }sin(xsin theta ¿Qué?

En el caso de que n = 0,
Y0()x)=4π π 2∫ ∫ 012π π # ()x# Silencio Silencio )()e+In ()2xpecado2 Silencio Silencio ))dSilencio Silencio .{displaystyle Y_{0}left(xright)={frac {4}{pi ^{2}int ¿Por qué? }cos left(xcos theta right)left(e+ln left(2xsin ^{2}theta right)right),dtheta.}

Yα(x) es necesaria como la segunda solución linealmente independiente de la ecuación de Bessel cuando α es un número entero. Pero Yα(x) tiene más significado que eso. Puede ser considerado como un "natural" socio de Jα(x). Consulte también la subsección sobre las funciones de Hankel a continuación.
Cuando α es un número entero, además, como ocurría de manera similar con las funciones del primer tipo, la siguiente relación es válida:
Y− − n()x)=()− − 1)nYn()x).{displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x). }

Tanto Jα(x) como Yα(x) son funciones holomorfas de x en el plano complejo cortado a lo largo del eje real negativo. Cuando α es un número entero, las funciones de Bessel J son funciones completas de x. Si x se mantiene fijo en un valor distinto de cero, entonces las funciones de Bessel son funciones completas de α.
Las funciones de Bessel del segundo tipo cuando α es un número entero es un ejemplo del segundo tipo de solución en Fuchs&# 39; s teorema.
Funciones de Hankel: H(1)α, H(2)α
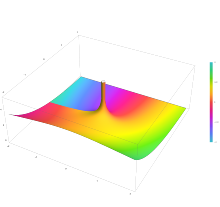
Parcela de la función Hankel del primer tipo
H1)
n()x) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D
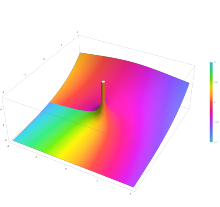
Parcela de la función Hankel del segundo tipo
H2)
n()x) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D
Otra formulación importante de las dos soluciones linealmente independientes de la ecuación de Bessel son las funciones de Hankel de primer y segundo tipo, H(1)
α(x) y H(2)
α(x), definido como
Hα α ()1)()x)=Jα α ()x)+iYα α ()x),Hα α ()2)()x)=Jα α ()x)− − iYα α ()x),{displaystyle {begin{aligned}H_{alpha }{(1)}(x) {cH_{alpha }(x)+iY_{alpha }(x),H_{alpha }{}{} {}(x)} {} {} {c]} {cH} {d} {d} {d}}}} {f}} {f}f}f}}f}f} {f}f} {f}f}f}f}cH}f}fnun}fnun}f}fnun}f}fnun}fnun}(x) {fnun}fnun}fnun} {fnunfnun}fnun}fnunfnun}fnun}fnun}fnun}fnun}fnun}fnun}

donde i es la unidad imaginaria. Estas combinaciones lineales también se conocen como funciones de Bessel de tercer tipo; son dos soluciones linealmente independientes de la ecuación diferencial de Bessel. Llevan el nombre de Hermann Hankel.
Estas formas de combinación lineal satisfacen numerosas propiedades de aspecto simple, como fórmulas asintoticas o representaciones integrales. Aquí, "simple" significa una aparición de un factor de la forma eifx). De verdad 0}" xmlns="http://www.w3.org/1998/Math/MathML">x■0{displaystyle x confianza0}![]() 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/> Donde Jα α ()x){displaystyle J_{alpha }(x)}
0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/> Donde Jα α ()x){displaystyle J_{alpha }(x)} , Yα α ()x){displaystyle Y_{alpha }(x)}
, Yα α ()x){displaystyle Y_{alpha }(x)} son reales, las funciones Bessel de primer y segundo tipo son las partes reales e imaginarias, respectivamente, de la primera función Hankel y las partes imaginarias reales y negativas de la segunda función Hankel. Así, las fórmulas anteriores son análogos de la fórmula de Euler, sustituyendo H1)
son reales, las funciones Bessel de primer y segundo tipo son las partes reales e imaginarias, respectivamente, de la primera función Hankel y las partes imaginarias reales y negativas de la segunda función Hankel. Así, las fórmulas anteriores son análogos de la fórmula de Euler, sustituyendo H1)
α()x), H2)
α()x) para e± ± ix{displaystyle e^{pm ix} y Jα α ()x){displaystyle J_{alpha }(x)}
y Jα α ()x){displaystyle J_{alpha }(x)} , Yα α ()x){displaystyle Y_{alpha }(x)}
, Yα α ()x){displaystyle Y_{alpha }(x)} para # ()x){displaystyle cos(x)}
para # ()x){displaystyle cos(x)} , pecado ()x){displaystyle sin(x)}
, pecado ()x){displaystyle sin(x)} , como se muestra explícitamente en la expansión asintotica.
, como se muestra explícitamente en la expansión asintotica.
Las funciones de Hankel se utilizan para expresar soluciones de ondas cilíndricas que se propagan hacia afuera y hacia adentro de la ecuación de onda cilíndrica, respectivamente (o viceversa, según la convención de signos para la frecuencia).
Usando las relaciones anteriores, se pueden expresar como
Hα α ()1)()x)=J− − α α ()x)− − e− − α α π π iJα α ()x)ipecado α α π π ,Hα α ()2)()x)=J− − α α ()x)− − eα α π π iJα α ()x)− − ipecado α α π π .{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif}

Si α es un número entero, se debe calcular el límite. Las siguientes relaciones son válidas, ya sea que α sea un número entero o no:
H− − α α ()1)()x)=eα α π π iHα α ()1)()x),H− − α α ()2)()x)=e− − α α π π iHα α ()2)()x).{displaystyle {begin{aligned}H_{-alpha }{(1)}(x) {=e^{alpha pi i}H_{alpha }{(1)}(x),H_{-alpha }{} {} {} {} {} {} {}}}} {}}} {}}} {}} {}}}}} {}}}}} {}}}}}}}}} {}}}}}}} {}}}}}}}} {}}} {}}}}}}}} {}}}}}}} {}}}}} {}}}}}}}}}}}}}}}}} {}}}}} {}}} {}}} {}}}}}}}}}}}}}}}}}}}}} {} {}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}

En particular, si α = m + 1/2 con m un entero no negativo, las relaciones anteriores implican directamente que
J− − ()m+12)()x)=()− − 1)m+1Ym+12()x),Y− − ()m+12)()x)=()− − 1)mJm+12()x).{displaystyle {begin{aligned}J_{-(m+{frac {1}{2})}(x) {=(-1)^{m+1}Y_{m+{frac} {1}{2}} {x),\Y_{-(m+{frac {1}{2})}(x) {=(-1)} {m}J_{m+{frac {1} {2}}}(x).end{aligned}}}}}}}}} {}}} {1}{2} {2}}}}}} {}}} {}} {}}}}}}}}} {}} {}}}}}}}}} {} {}}}}}}} {c)}} {c)}}} {c)}}}}}}} {c)}}}}}}} {c)}}}} {c)}} {c)}}}}} {c)}} {c)}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c)}}}}}}}}}}}}}}

Estos son útiles para desarrollar las funciones esféricas de Bessel (ver más abajo).
Las funciones de Hankel admiten las siguientes representaciones integrales para Re(x) > 0:
Hα α ()1)()x)=1π π i∫ ∫ − − JUEGO JUEGO +JUEGO JUEGO +π π iexpecado t− − α α tdt,Hα α ()2)()x)=− − 1π π i∫ ∫ − − JUEGO JUEGO +JUEGO JUEGO − − π π iexpecado t− − α α tdt,{displaystyle {begin{aligned}H_{alpha }{(1)}(x) {1}{pi} # I'# {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {1}{pi} # I'# ¿Por qué?

Funciones de Bessel modificadas: Iα, Kα
Las funciones de Bessel son válidas incluso para argumentos complejos x, y un caso especial importante es el de un argumento puramente imaginario. En este caso, las soluciones a la ecuación de Bessel se denominan funciones de Bessel modificadas (o, en ocasiones, funciones de Bessel hiperbólicas) del primer y segundo tipo y se definen como
Iα α ()x)=i− − α α Jα α ()ix)=.. m=0JUEGO JUEGO 1m!.. ()m+α α +1)()x2)2m+α α ,Kα α ()x)=π π 2I− − α α ()x)− − Iα α ()x)pecado α α π π ,{displaystyle {begin{aligned}I_{alpha }(x) {i^{-alpha }J_{alpha }(ix)=sum ¿Qué? {1}{m!,Gamma (m+alpha +1)}left({frac {x}{2}right)^{2m+alpha },K_{alpha }(x) {frac {pi}{2}}}{f} {f} {fnfnK} {f} {f}}f}}}}f}f}}f}f}}f}}f}f} {f} {f}f}f}f}f}f}fn0}fn0}f}f}f}f}fnfnfnfnh00} {fnh00} {cH00}}}fnun}fnh00}fn0}fnun}fn0cH00}fnfn0}cH00}}f}cfn

Kα α {displaystyle K_{alpha } se puede expresar en términos de funciones de Hankel:
se puede expresar en términos de funciones de Hankel:
<math alttext="{displaystyle K_{alpha }(x)={begin{cases}{frac {pi }{2}}i^{alpha +1}H_{alpha }^{(1)}(ix)&-pi <arg xleq {frac {pi }{2}}\{frac {pi }{2}}(-i)^{alpha +1}H_{alpha }^{(2)}(-ix)&-{frac {pi }{2}}Kα α ()x)={}π π 2iα α +1Hα α ()1)()ix)− − π π .arg x≤ ≤ π π 2π π 2()− − i)α α +1Hα α ()2)()− − ix)− − π π 2.arg x≤ ≤ π π {displaystyle K_{alpha }(x)={begin{cases}{frac {pi ## {2}i^{alpha +1}H_{alpha }{(1)}(ix) Dame-pi - ¿Qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {2} {g xleq piend{cases}}
<img alt="{displaystyle K_{alpha }(x)={begin{cases}{frac {pi }{2}}i^{alpha +1}H_{alpha }^{(1)}(ix)&-pi <arg xleq {frac {pi }{2}}\{frac {pi }{2}}(-i)^{alpha +1}H_{alpha }^{(2)}(-ix)&-{frac {pi }{2}}
Usando estas dos fórmulas el resultado Jα α 2()z){displaystyle J_{alpha } {2}(z)} +Yα α 2()z){displaystyle Y_{alpha } {2}(z)}
+Yα α 2()z){displaystyle Y_{alpha } {2}(z)} , comúnmente conocido como la integral de Nicholson o la fórmula de Nicholson, se puede obtener para dar lo siguiente
, comúnmente conocido como la integral de Nicholson o la fórmula de Nicholson, se puede obtener para dar lo siguiente
Jα α 2()x)+Yα α 2()x)=8π π 2∫ ∫ 0JUEGO JUEGO cosh ()2α α t)K0()2xpecado t)dt,{displaystyle J_{i}alpha }{2}(x)+Y_{alpha }{2}(x)={frac {8}{pi ^{2}}}int _{0}{infty }cosh(2alpha t)K_{0}(2xsinh t),dt,}

dado que la condición Re(x) > 0 se cumple. También se puede demostrar que
Jα α 2()x)+Yα α 2()x)=8# ()α α π π )π π 2∫ ∫ 0JUEGO JUEGO K2α α ()2xpecado t)dt,{displaystyle J_{i}alpha }{2}(x)+Y_{alpha }{2}(x)={frac {8cos(alpha pi)}{pi) ¿Qué?

solo cuando |Re(α)| < 1/ 2 y Re(x) ≥ 0 pero no cuando x = 0.
Podemos expresar la primera y la segunda función de Bessel en términos de las funciones de Bessel modificadas (estas son válidas si −π < arg z ≤ π/2):
Jα α ()iz)=eα α π π i2Iα α ()z),Yα α ()iz)=e()α α +1)π π i2Iα α ()z)− − 2π π e− − α α π π i2Kα α ()z).{displaystyle {begin{aligned}J_{alpha }(iz) reducida=e^{frac {alpha pi i}{2}I_{alpha }(z),\Y_{alpha }(iz) {frac {alpha +1)pi Yo... {2}{pi} }e^{-{frac {alpha pi {fnMicrosoft Sans Serif}}

Yoα(x) y Kα(x) son las dos soluciones linealmente independientes de la ecuación de Bessel modificada:
x2d2Sí.dx2+xdSí.dx− − ()x2+α α 2)Sí.=0.{displaystyle x^{2}{frac} {fnMicroc}fnMicroc {fnMicrosoft Sans Serif}

A diferencia de las funciones ordinarias de Bessel, que oscilan como funciones de un argumento real, Iα y Kα son funciones que crecen y decaen exponencialmente, respectivamente. Al igual que la función ordinaria de Bessel Jα, la función Iα va a cero en x = 0 para α > 0 y es finito en x = 0 para α = 0 . Análogamente, Kα diverge en x = 0 siendo la singularidad de tipo logarítmico para K0, y 1/ 2Γ(|α |)(2/x)|α| de lo contrario.
 Funciones de Bessel modificadas del primer tipo, Iα()x), para α = 0, 1, 2, 3 |  Funciones de Bessel modificadas del segundo tipo, Kα()x), para α = 0, 1, 2, 3 |
Dos fórmulas integrales para las funciones de Bessel modificadas son (para Re(x) > 0):
Iα α ()x)=1π π ∫ ∫ 0π π ex# Silencio Silencio # α α Silencio Silencio dSilencio Silencio − − pecado α α π π π π ∫ ∫ 0JUEGO JUEGO e− − xcosh t− − α α tdt,Kα α ()x)=∫ ∫ 0JUEGO JUEGO e− − xcosh tcosh α α tdt.{displaystyle {begin{aligned}I_{alpha }(x) limit={frac {1}{pi }}int _{0}{pi} {fn0} {fn0} }e^{xcos theta }cos alpha theta ,dtheta -{frac {sin alpha pi }int _{0}infty }e^{-xcosh t-alpha t},dt,K_{alpha }(x) ¿Por qué?

Las funciones de Bessel se pueden describir como transformadas de Fourier de potencias de funciones cuadráticas. Por ejemplo:
2K0()⋅ ⋅ )=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO ei⋅ ⋅ tt2+1dt.{displaystyle 2,K_{0}(omega)=int _{-infty }{infty }{frac {e^{iomega No.

Se puede demostrar mostrando igualdad con la definición integral anterior para K0. Esto se hace integrando una curva cerrada en el primer cuadrante del plano complejo.
Funciones Bessel modificadas K1/3 y K2/3 se puede representar en términos de integrales rápidamente convergentes
K13().. )=3∫ ∫ 0JUEGO JUEGO exp ()− − .. ()1+4x23)1+x23)dx,K23().. )=13∫ ∫ 0JUEGO JUEGO 3+2x21+x23exp ()− − .. ()1+4x23)1+x23)dx.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c} {c} {c} {c} {c} {c} {cc} {c} {ccc} {cccccccccccccc}}}}ccccccccc}ccccccccccccccccccccccccccccccccccccccccccc}ccccccccccccccccccc {x^{2}{3}}}}}exp left(-xi left(1+{frac {4x^{2}}{3}}}right){sqrt {1+{frac {x^{2}}{3}}}}}right)dx.end{aligned}}}}}}}}}} {x}}} {f}}}}}}} {f}}}}}}}}}}}} {f}}}}} {f}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}f}f}}}f}f}}f}f}f}f}}f}f}f}f}}f}}}f}f}}f}f}f}f}f}f}}f}}fn

La función Bessel modificada K12().. )=.. − − 1/2exp ()− − .. ){fnMicrosoft Sans Serif}(xi)=xi ^{-1/2}exp(-xi)} es útil para representar la distribución Laplace como una mezcla de distribución normal a escala Exponential.
es útil para representar la distribución Laplace como una mezcla de distribución normal a escala Exponential.
La función de Bessel modificada del segundo tipo también ha sido llamada con los siguientes nombres (ahora raros):
- Función Basset después de Alfred Barnard Basset
- Función de Bessel modificada del tercer tipo
- Función de Hankel modificada
- Función Macdonald después de Héctor Munro Macdonald
Funciones esféricas de Bessel: jn, yn

Parcela de la función esférica Bessel del primer tipo
jn()z) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D
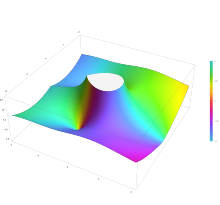
Parcela de la función esférica Bessel del segundo tipo
Sí.n()z) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D
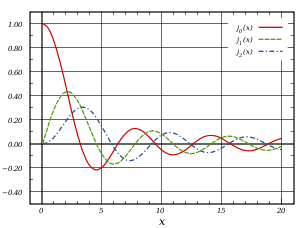
Funciones esféricas de Bessel del primer tipo,
jn()x), para
n = 0, 1, 2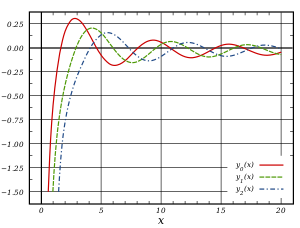
Funciones Spherical Bessel del segundo tipo,
Sí.n()x), para
n = 0, 1, 2Al resolver la ecuación de Helmholtz en coordenadas esféricas por separación de variables, la ecuación radial tiene la forma
x2d2Sí.dx2+2xdSí.dx+()x2− − n()n+1))Sí.=0.{displaystyle x^{2}{frac} {d^{2}y}{dx^{2}}+2x{frac {y}}+left(x^{2}-n(n+1)right)y=0.}

Las dos soluciones linealmente independientes de esta ecuación se denominan funciones esféricas de Bessel jn y yn, y están relacionadas con las funciones ordinarias de Bessel Jn y Yn por
jn()x)=π π 2xJn+12()x),Sí.n()x)=π π 2xYn+12()x)=()− − 1)n+1π π 2xJ− − n− − 12()x).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} J_{n+{frac} {1}{2}}(x),y_{n}(x) Conden={sqrt {frac ♪ - Sí. {1}{2}}=(x)=(-1)^{n+1}{sqrt {frac {pi)} J-n-{frac} {1} {2}} {x)end{aligned}}}

yn también se denota nn o ηn; algunos autores llaman a estas funciones las funciones esféricas de Neumann.
De las relaciones con las funciones ordinarias de Bessel se ve directamente que:
jn()x)=()− − 1)nSí.− − n− − 1()x)Sí.n()x)=()− − 1)n+1j− − n− − 1()x){displaystyle {begin{aligned}j_{n}(x) {=(-1)^{n}y_{-n-1}(x)\\y_{n}(x) ventaja=(-1)^{n+1}j_{-n-1}(x)end{aligned}}}}}}}}}}
Las funciones esféricas de Bessel también se pueden escribir como (fórmulas de Rayleigh)
jn()x)=()− − x)n()1xddx)npecado xx,Sí.n()x)=− − ()− − x)n()1xddx)n# xx.{displaystyle {begin{aligned}j_{n}(x)} {n}n}n} {frac {n}{frac {dx}}}derecho)}{n}{n}{n}{n}{n}{n}n}{n}n} {n}}n}}}n}}n}}}}n}n}{n}{n}}n}n}}n}n}}n}}n}{n}n}n}}n}n}}}}}}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n} ###{n},y_{n}(x)} {n}left({frac {1}{x}{frac {d}{dx}right)}{n}{n}{frac {cos x}}}}}end{aligned}}}}}}}}}}}}}}} {end{aligned}}}}}}}}}}}}}}}}}}}} {f}{n}{n}}}}{n}{n}}}{n}}}}}}}}}}{n}}}}}}}}}}}}}}}}}}}}{n}{n}{n}}}}}}}}}}}}{n}{n}}{n}}}}}}}}}}}}}}}}}}}}} {m}}}} {m}}}}}}}}}}}}}}}}} {m}}} {

La función de Bessel esférica cero j0(x) también se conoce como la función sinc (no normalizada). Las primeras funciones esféricas de Bessel son:
j0()x)=pecado xx.j1()x)=pecado xx2− − # xx,j2()x)=()3x2− − 1)pecado xx− − 3# xx2,j3()x)=()15x3− − 6x)pecado xx− − ()15x2− − 1)# xx{displaystyle {begin{aligned}j_{0}(x) Sentido={frac {sin x}{x}}\j_{1}(x) ##{x^{2}}-{cos x}{x}},\j_{2}(x) {fnunció=left({frac {3}{2}}}} {frac {sin x}{x}}-{frac {3cos x}{x^{2}}}}},\j_{3}(x) âTMa âTMa âTMa {frac {15}{3}}}}}-{q}{x} {right){s} {s} {s} {s} {s}}}} {s}} {s}}}}} {s}}} {s} {s}}} {s}}}}} {s}}}}}}}}} {s}}}}}}}}}}}}}}}}} {s}}}}}}}} {s}}}}}}}} {fnf}}f}}} {f}}} {fn}} {f}}}}}}f}f}f}f}f}}fn {fnK} {fnMicroc {15} {fnK}} {fnMicroc {cos x}}end{aligned}}}}

Sí.0()x)=− − j− − 1()x)=− − # xx,Sí.1()x)=j− − 2()x)=− − # xx2− − pecado xx,Sí.2()x)=− − j− − 3()x)=()− − 3x2+1)# xx− − 3pecado xx2,Sí.3()x)=j− − 4()x)=()− − 15x3+6x)# xx− − ()15x2− − 1)pecado xx.{displaystyle {begin{aligned}y_{0}(x) {=-j_{-1}(x)=-{frac {cos x}{x},y_{1}(x) {fnMicrosoft Sans Serif} {fnMicroc {fnK}}y_{2}(x) {=-j_{-3}(x)=left(-{frac {3}{2}}}+1right){frac {cos x}{x}}-{frac {3sin] {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicroc} {fnMicroc} {fnMicroc} {fnK} {fnMicroc} {c}} {ccc} {c}c}c}c}c}c}ccc}ccc}ccc}c}c}c}ccccccccccccccccccccccccccccccccccccc}c}c}ccc}ccc}ccc}cccc}cc

Función generadora
Las funciones esféricas de Bessel tienen las funciones generadoras
1z# ()z2− − 2zt)=.. n=0JUEGO JUEGO tnn!jn− − 1()z),1zpecado ()z2− − 2zt)=.. n=0JUEGO JUEGO tnn!Sí.n− − 1()z).{displaystyle {begin{aligned}{1}{z}cos left({sqrt {z^{2}-2zt}}right) {fn}j_{n-1}(z),{frac {1}{z}sin left({sqrt {2}-2zt}}right)}=sum {fn}y_{n-1}(z)end{aligned}

Relaciones diferenciales
A continuación, fn es cualquiera de jn, yn, h(1)
n, h(2)
n para n = 0, ±1, ±2, …
()1zddz)m()zn+1fn()z))=zn− − m+1fn− − m()z),()1zddz)m()z− − nfn()z))=()− − 1)mz− − n− − mfn+m()z).{fn} {fn} {fn} {fn}} {f}} {f}}} {f}} {f} {f}}} {f}} {f}} {f}} {f}} {m}}} {f}}} {m} {m} {m} {m} {f}}} {m}}}} {m} {m} {m} {m} {m} {c}} {m}}}} {m} {c} {m} {cccf} {f} {f} {f} {f} {f} {f} {f} {f} {m} {f} {f} {f}{f} {f} {f} {f} {f} {f} {f} {f} {f} {f}}}}}}}

Funciones esféricas de Hankel: h(1)n, h(2)n
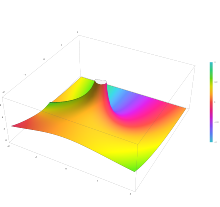
Parcela de la función esférica de Hankel del primer tipo
h1)
n()x) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D

Parcela de la función esférica de Hankel del segundo tipo
h2)
n()x) con
n = 0,5 en el plano complejo desde
-2-2i a
2+2i con colores creados con Mathematica 13.1 función ComplexPlot3D
También hay análogos esféricos de las funciones de Hankel:
hn()1)()x)=jn()x)+iSí.n()x),hn()2)()x)=jn()x)− − iSí.n()x).{displaystyle {begin{aligned}h_{n}{(1)}(x) sentimiento=j_{n}(x)+iy_{n}(x),\h_{n}{(2)}(x) limit=j_{n}(x)-iy_{n}(x).end{aligned}}}}}}}}}

De hecho, existen expresiones simples de forma cerrada para las funciones de Bessel de orden medio entero en términos de las funciones trigonométricas estándar y, por lo tanto, para las funciones esféricas de Bessel. En particular, para enteros no negativos n:
hn()1)()x)=()− − i)n+1eixx.. m=0nimm!()2x)m()n+m)!()n− − m)!,{displaystyle h_{n}{(1)}(x)=(-i)^{n+1}{frac {fnK} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}}}}}} {fnMicrosoft}}}}} {fnK}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}} ¡No!

y h(2)
n es el complejo -conjugado de esto (para real x). Se sigue, por ejemplo, que j0(x) = sin x/ x y y0(x ) = −cos x/x, y así sucesivamente.
Las funciones esféricas de Hankel aparecen en problemas relacionados con la propagación de ondas esféricas, por ejemplo, en la expansión multipolar del campo electromagnético.
Funciones de Riccati-Bessel: Sn, Cn, ξn, ζn
Las funciones de Riccati-Bessel difieren ligeramente de las funciones de Bessel esféricas:
Sn()x)=xjn()x)=π π x2Jn+12()x)Cn()x)=− − xSí.n()x)=− − π π x2Yn+12()x).. n()x)=xhn()1)()x)=π π x2Hn+12()1)()x)=Sn()x)− − iCn()x)Especificaciones Especificaciones n()x)=xhn()2)()x)=π π x2Hn+12()2)()x)=Sn()x)+iCn()x){displaystyle {begin{aligned}S_{n}(x) Conden=xj_{n}(x)={sqrt {frac {pi J_{n+{frac} {1}{2}}}(x)C_{n}(x) recur=-xy_{n}(x)=-{sqrt {frac {pic {pi) Y... {1}{2}} {x)\xi _{n}(x=xh_{n}^{(1)}(x)={sqrt {frac {pic} ##{2} {2} {2} {=x)=S_{n}(x)-iC_{n}(x)\\zeta _{n}(x)}(x)}(x)} {fn}(x)}={=x)={=sqrt {fc {fnfn} {fnfnfn}fn}fn}fnfn}fnfnfnfnfnfnfnfnfnfnfnfnfn9}fnfnfnfnfn}fn9}fnfn9}fnfnfn}fnfn}fnfnfnfn}fnfn}fn}fnfnfn}fnfnfnfn}fnfn # {2} {2}=S_{n}(x)+iC_{n}(x)end{aligned}}}

Satisfacen la ecuación diferencial
x2d2Sí.dx2+()x2− − n()n+1))Sí.=0.{displaystyle x^{2}{frac} {d^{2}y}{dx^{2}}+left(x^{2}-n(n+1)right)y=0.}

Por ejemplo, este tipo de ecuación diferencial aparece en la mecánica cuántica al resolver la componente radial de la ecuación de Schrödinger con una barrera de potencial infinito cilíndrica hipotética. Esta ecuación diferencial, y las soluciones de Riccati-Bessel, también surgen en el problema de la dispersión de ondas electromagnéticas por una esfera, conocido como dispersión de Mie por la primera solución publicada por Mie (1908). Véase, por ejemplo, Du (2004) para desarrollos y referencias recientes.
Siguiendo a Debye (1909), la notación ψn, χn a veces se usa en lugar de Sn, Cn.
Formas asintóticas
Las funciones Bessel tienen las siguientes formas asintomáticas. Para pequeños argumentos <math alttext="{displaystyle 00.z≪ ≪ α α +1{displaystyle 0 madezll {sqrt {alpha #<img alt="{displaystyle 0, uno obtiene, cuando α α {displaystyle alpha } no es un entero negativo:
no es un entero negativo:
Jα α ()z)♪ ♪ 1.. ()α α +1)()z2)α α .{displaystyle J_{alpha }(z)sim {frac {1}{Gamma (alpha +1)}}left({frac {z}{2}right)^{alpha }

Cuando α es un entero negativo, tenemos
Jα α ()z)♪ ♪ ()− − 1)α α ()− − α α )!()2z)α α .{displaystyle J_{alpha }(z)sim {frac {(-1)^{alpha {fnMicrosoft Sans Serif}}} {fnMicroc {2}derecho)}derecha }

Para la función de Bessel de segundo tipo tenemos tres casos:
Yα α ()z)♪ ♪ {}2π π ()In ()z2)+γ γ )siα α =0− − .. ()α α )π π ()2z)α α +1.. ()α α +1)()z2)α α cot ()α α π π )siα α no es un entero no positivo (un término domina a menos queα α es imaginario),− − ()− − 1)α α .. ()− − α α )π π ()z2)α α siα α es un entero negativo,{displaystyle Y_{alpha }(z)sim {begin{cases}{dfrac {2}{pi }}left(ln left({dfrac {z}{2}right)+gammaright) =0\-{dfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc}}}}f}}}}}f}f}}f}f}f}fnMicrocf}fnMicrocf}}}}}f}}f}f}f}}fnunfnMicrocf}}fnun}}}}cccfnuncccccccH0ccH0}cccccH0}cH0}ccH0}ccH0}ccH00}}cccH {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {f}}}fnMicros}} {f}f}}f}f}f}fnMicrosoft} {fnMicrosoft} {f}fnMicros}fnMicros}fnMicrosoft}fnMicros}}}fnMicros}fnMicros}fnMicrosoft}fnun}}fnMicrosoft}fnMicros}fnMicrosoft}fnMicrosoft}fnMicrosoft}fnMicrosoft}f}f}}fnMi

Para argumentos reales grandes z ≫ |<span class="nowrap" style="padding-left:0.1em; padding-right:0.1em;" α2 − 1/4|, no se puede escribir una forma asintótica verdadera para las funciones de Bessel de la primera y de segundo tipo (a menos que α sea medio entero) porque tienen ceros hasta el infinito, lo que tendría que ser coincide exactamente con cualquier expansión asintótica. Sin embargo, para un valor dado de arg z se puede escribir una ecuación que contenga un término de orden |z|−1:
<math alttext="{displaystyle {begin{aligned}J_{alpha }(z)&={sqrt {frac {2}{pi z}}}left(cos left(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)+e^{left|operatorname {Im} (z)right|}{mathcal {O}}left(|z|^{-1}right)right)&&{text{for }}left|arg zright|<pi\Y_{alpha }(z)&={sqrt {frac {2}{pi z}}}left(sin left(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)+e^{left|operatorname {Im} (z)right|}{mathcal {O}}left(|z|^{-1}right)right)&&{text{for }}left|arg zright|Jα α ()z)=2π π z()# ()z− − α α π π 2− − π π 4)+eSilencioIm ()z)SilencioO()SilenciozSilencio− − 1))paraSilencioarg zSilencio.π π ,Yα α ()z)=2π π z()pecado ()z− − α α π π 2− − π π 4)+eSilencioIm ()z)SilencioO()SilenciozSilencio− − 1))paraSilencioarg zSilencio.π π .{displaystyle {begin{aligned}J_{alpha }(z) limit={sqrt {frac {2}{pi z}}}}left(cos left(z-{frac} {fnMicroc}}}}}left(esleft) {alpha pi {}{2}-{frac {f} ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnuncio}}left perpetuaarg zright obedeciópi\\\\\y_{fnMicroc} {fnMicroc} {fnMicroc}f}f}fnMicrocfn}fnMicrocfn}s}fnMicrocfnMicrocfnMicrocfnun}f}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnun}fnunfnun}fnun}fnunfnun}fnun}fnun}fn {alpha pi {}{2}-{frac {f} ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}
<img alt="{displaystyle {begin{aligned}J_{alpha }(z)&={sqrt {frac {2}{pi z}}}left(cos left(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)+e^{left|operatorname {Im} (z)right|}{mathcal {O}}left(|z|^{-1}right)right)&&{text{for }}left|arg zright|<pi\Y_{alpha }(z)&={sqrt {frac {2}{pi z}}}left(sin left(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)+e^{left|operatorname {Im} (z)right|}{mathcal {O}}left(|z|^{-1}right)right)&&{text{for }}left|arg zright|
(Para α = 1/2 los últimos términos de estas fórmulas desaparecen por completo; vea las funciones esféricas de Bessel anterior). Aunque estas ecuaciones son verdaderas, es posible que haya mejores aproximaciones disponibles para z complejos. Por ejemplo, J0(z) cuando z está cerca de la línea real negativa se aproxima mejor por
J0()z).. − − 2π π z# ()z+π π 4){displaystyle J_{0}(z)approx {sqrt {frac {-2}}cos left(z+{frac {pi }{4}right)}}

J0()z).. 2π π z# ()z− − π π 4).{displaystyle J_{0}(z)approx {sqrt {frac {2}{pi z}}cos left(z-{frac {pi }right). }

Las formas asintóticas de las funciones de Hankel son:
<math alttext="{displaystyle {begin{aligned}H_{alpha }^{(1)}(z)&sim {sqrt {frac {2}{pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<2pi\H_{alpha }^{(2)}(z)&sim {sqrt {frac {2}{pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-2pi <arg zHα α ()1)()z)♪ ♪ 2π π zei()z− − α α π π 2− − π π 4)para− − π π .arg z.2π π ,Hα α ()2)()z)♪ ♪ 2π π ze− − i()z− − α α π π 2− − π π 4)para− − 2π π .arg z.π π .{displaystyle {begin{aligned}H_{alpha }{(1)}(z) {sqrt {sqrt {frac {2}{pi z}}}}e^{ileft(z-{frac} {alpha pi {}{2}-{frac {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans} {fnMicroc {f} {fnMicroc} {f}}e^{-ifnfnMicroc} {alpha pi {}{2}-{frac {f} {4}}derecha)} - Sí.
<img alt="{displaystyle {begin{aligned}H_{alpha }^{(1)}(z)&sim {sqrt {frac {2}{pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<2pi\H_{alpha }^{(2)}(z)&sim {sqrt {frac {2}{pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-2pi <arg z
Estos pueden extenderse a otros valores de arg z usando ecuaciones relacionadas con H(1)
α(zeimπ) y H (2)
α(zeimπ) a H(1)
α(z) y H(2)
α( z).
Es interesante que aunque la función de Bessel del primer tipo es el promedio de las dos funciones de Hankel, Jα(z) no es asintótico al promedio de estas dos formas asintóticas cuando z es negativo (porque allí uno u otro no será correcto, dependiendo del arg z usado). Pero las formas asintóticas de las funciones de Hankel nos permiten escribir formas asintóticas de las funciones de Bessel de primer y segundo tipo para complejas (no reales) z siempre que |z| va al infinito en un ángulo de fase constante arg z (usando la raíz cuadrada que tiene parte real positiva):
<math alttext="{displaystyle {begin{aligned}J_{alpha }(z)&sim {frac {1}{sqrt {2pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<0,\J_{alpha }(z)&sim {frac {1}{sqrt {2pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}0<arg z<pi\Y_{alpha }(z)&sim -i{frac {1}{sqrt {2pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<0,\Y_{alpha }(z)&sim i{frac {1}{sqrt {2pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}0<arg zJα α ()z)♪ ♪ 12π π zei()z− − α α π π 2− − π π 4)para− − π π .arg z.0,Jα α ()z)♪ ♪ 12π π ze− − i()z− − α α π π 2− − π π 4)para0.arg z.π π ,Yα α ()z)♪ ♪ − − i12π π zei()z− − α α π π 2− − π π 4)para− − π π .arg z.0,Yα α ()z)♪ ♪ i12π π ze− − i()z− − α α π π 2− − π π 4)para0.arg z.π π .{displaystyle {begin{aligned}J_{alpha } {sim} {frac {1}{sqrt {2pi z}}}}}e^{ileft(z-{frac} {alpha pi {}{2}-{frac {f} {4}}derecha)} {fnMicrosoft Sans Serif} {alpha pi {}{2}-{frac {f} {}} {4}}derecha)} {text{for }0}0 seleccionarg1\pi\\Y_{alpha }(z) limitsim -i{frac {1}{ileft(z-{frac} {alpha pi {}{2}-{frac {f} {4}}derecha)} }-pi } {fnMicroc {1} {fnMicroc {1} {sqrt {2pi z}}}e^{-ileft(z-{fc} {alpha pi {}{2}-{frac {f} {fnMicrosoft Sans Serif}0 0 0 0 0 0 0}p1}}
<img alt="{displaystyle {begin{aligned}J_{alpha }(z)&sim {frac {1}{sqrt {2pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<0,\J_{alpha }(z)&sim {frac {1}{sqrt {2pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}0<arg z<pi\Y_{alpha }(z)&sim -i{frac {1}{sqrt {2pi z}}}e^{ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}-pi <arg z<0,\Y_{alpha }(z)&sim i{frac {1}{sqrt {2pi z}}}e^{-ileft(z-{frac {alpha pi }{2}}-{frac {pi }{4}}right)}&&{text{for }}0<arg z
Para las funciones de Bessel modificadas, Hankel también desarrolló expansiones asintóticas (argumento grande):
<math alttext="{displaystyle {begin{aligned}I_{alpha }(z)&sim {frac {e^{z}}{sqrt {2pi z}}}left(1-{frac {4alpha ^{2}-1}{8z}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)}{2!(8z)^{2}}}-{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)left(4alpha ^{2}-25right)}{3!(8z)^{3}}}+cdots right)&&{text{for }}left|arg zright|<{frac {pi }{2}},\K_{alpha }(z)&sim {sqrt {frac {pi }{2z}}}e^{-z}left(1+{frac {4alpha ^{2}-1}{8z}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)}{2!(8z)^{2}}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)left(4alpha ^{2}-25right)}{3!(8z)^{3}}}+cdots right)&&{text{for }}left|arg zright|Iα α ()z)♪ ♪ ez2π π z()1− − 4α α 2− − 18z+()4α α 2− − 1)()4α α 2− − 9)2!()8z)2− − ()4α α 2− − 1)()4α α 2− − 9)()4α α 2− − 25)3!()8z)3+⋯ ⋯ )paraSilencioarg zSilencio.π π 2,Kα α ()z)♪ ♪ π π 2ze− − z()1+4α α 2− − 18z+()4α α 2− − 1)()4α α 2− − 9)2!()8z)2+()4α α 2− − 1)()4α α 2− − 9)()4α α 2− − 25)3!()8z)3+⋯ ⋯ )paraSilencioarg zSilencio.3π π 2.{displaystyle {begin{aligned}I_{alpha }(z) ventajasim {frac {fn} {fnK}}left(1-{frac {4fac} {fnK}}}left(1-{frac {4f} {fnfnK}} {fnf}}}} {f}}}}}}}} {fnf}}} {f}}}}}}}}}}}}}}}}}}m}}}}m}m} {p}}}}}}}}}}}}}pppppppppppf}}}}}}}}}}}}ppppppppppppppf}pppppf}f}f}f}f}f}f}f}}ppf} {p}p {2fnMicrosoft Sans Serif} {2}}} {2}}} {2}} {fnMicrosoft Sans Serif} }{2},K_{alpha }(z) golpesim {sqrt {frac {pi ## {2z}'e^{-z}left(1+{frac {4alpha {2fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
<img alt="{displaystyle {begin{aligned}I_{alpha }(z)&sim {frac {e^{z}}{sqrt {2pi z}}}left(1-{frac {4alpha ^{2}-1}{8z}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)}{2!(8z)^{2}}}-{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)left(4alpha ^{2}-25right)}{3!(8z)^{3}}}+cdots right)&&{text{for }}left|arg zright|<{frac {pi }{2}},\K_{alpha }(z)&sim {sqrt {frac {pi }{2z}}}e^{-z}left(1+{frac {4alpha ^{2}-1}{8z}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)}{2!(8z)^{2}}}+{frac {left(4alpha ^{2}-1right)left(4alpha ^{2}-9right)left(4alpha ^{2}-25right)}{3!(8z)^{3}}}+cdots right)&&{text{for }}left|arg zright|
También hay la forma asintotica (para grandes reales z{displaystyle z} )
)
Iα α ()z)=12π π z1+α α 2z24exp ()− − α α arsinh ()α α z)+z1+α α 2z2)()1+O()1z1+α α 2z2)).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}} {f}}}} {f}}f}}}}}f}f}f}f}f}f}f}f}f}f}f}fnKfnKf}f}f}f}fnKf}fnKfnKf}fnKfnKf}}}}fnMisssssssssssssssssssssssssssssssssssssssssssssss {1+{fc {fnMicroc}alfa ¿Qué? {1}{z{sqrt Bien.
![{displaystyle {begin{aligned}I_{alpha }(z)={frac {1}{{sqrt {2pi z}}{sqrt[{4}]{1+{frac {alpha ^{2}}{z^{2}}}}}}}exp left(-alpha operatorname {arsinh} left({frac {alpha }{z}}right)+z{sqrt {1+{frac {alpha ^{2}}{z^{2}}}}}right)left(1+{mathcal {O}}left({frac {1}{z{sqrt {1+{frac {alpha ^{2}}{z^{2}}}}}}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f57e4803db262b5efdc20c32da3835c3fd4f0f9d)
Cuando α = 1/2, todos los términos excepto el primero desaparecen, y tenemos
<math alttext="{displaystyle {begin{aligned}I_{frac {1}{2}}(z)&={sqrt {frac {2}{pi z}}}sinh(z)sim {frac {e^{z}}{sqrt {2pi z}}}&&{text{for }}left|arg zright|I12()z)=2π π zpecado ()z)♪ ♪ ez2π π zparaSilencioarg zSilencio.π π 2,K12()z)=π π 2ze− − z.{fnK} {fnMicroc {1} {fnMicroc} {fnunci} {sqrt {f} {fnh}}sim {fnMicroc {f} {fn} {f} {f}}}}}} {f}fnfnf}fnf}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnfnfnfnf}f}f}f}f}fnfnhf}f}fnf}fnf}fnfnfnf}f}f}fnfnfnfnfnfnf}f}f}f}fn ## {2}},K_{2} {2} {2} {sqrt {frac {fnMic {pi} {fnMicrosoft Sans Serif}
<img alt="{displaystyle {begin{aligned}I_{frac {1}{2}}(z)&={sqrt {frac {2}{pi z}}}sinh(z)sim {frac {e^{z}}{sqrt {2pi z}}}&&{text{for }}left|arg zright|
Para pequeños argumentos <math alttext="{displaystyle 00.SilenciozSilencio≪ ≪ α α +1{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {f}fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft}fnMicrosoft\\fnMicrosoft\fnMicrosoftfnMicrosoft\\\fnMicrosoft\\\\fnMicrosoft\fnMicrosoftfnMicrosoftfnMicrosoft {fnMicrosoftfnMicrosoft\fnMicrosoftfnMicrosoftfnMicrosoft {fnMicrosoftfnMicrosoftfnMicrosoft\\\\fnMicrosoft\\fnMi #<img alt="{displaystyle 0, tenemos
0end{cases}}end{aligned}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Iα α ()z)♪ ♪ 1.. ()α α +1)()z2)α α ,Kα α ()z)♪ ♪ {}− − In ()z2)− − γ γ siα α =0.. ()α α )2()2z)α α siα α ■0{displaystyle {begin{aligned}I_{alpha }(z) ventajasim {frac {1}{Gamma (alpha +1)}}}left({frac {z}{2}right)^{alpha },K_{alpha }(z) limitsim {begin{cases}-lnleft({dfracdfrac {z}{2}right)-gamma ## {text{if}alpha =0{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}}}}}}}}}}}}}}}fnunto {f}}}}}f}}fnMisigualsigualextranunto {f}}}}}}}}}}}fnun}}}}}}}}}}}}}}f}}}}fnun}f}fnun}}fnunfnunfnunfnunf}fnunfnunfnun}fnunfnunfnunfnunfnun}}}fnMi
![]()
0end{cases}}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3f9e6682f7643b167f20a5775c5291e1a16e3b42" style="vertical-align: -7.716ex; margin-bottom: -0.289ex; width:35.844ex; height:17.176ex;"/>
Propiedades
Para orden de números enteros α = n, Jn a menudo se define a través de una serie de Laurent para una función generadora:
e()x2)()t− − 1t)=.. n=− − JUEGO JUEGO JUEGO JUEGO Jn()x)tn{displaystyle e^{left({frac {x}{2}right)left(t-{frac {1}{t}right)}=sum ¿Por qué?

Una expansión en serie usando funciones de Bessel (serie de Kapteyn) es
- 11− − z=1+2.. n=1JUEGO JUEGO Jn()nz).{displaystyle {frac {1}{1-z}=1+2sum _{n=1}{infty }J_{n}(nz).}

Otra relación importante para los órdenes enteros es la expansión Jacobi-Anger:
eiz# φ φ =.. n=− − JUEGO JUEGO JUEGO JUEGO inJn()z)einφ φ {displaystyle e^{izcos phi }=sum _{n=-infty

e± ± izpecado φ φ =J0()z)+2.. n=1JUEGO JUEGO J2n()z)# ()2nφ φ )± ± 2i.. n=0JUEGO JUEGO J2n+1()z)pecado ()()2n+1)φ φ ){displaystyle e^{pm izsin phi }=J_{0}(z)+2sum _{n=1}{infty }J_{2n}(z)cos(2nphi)pm 2isum _{n=0}{infty }J_{2n+1}(z)sin(2n+1)phi)}

Más generalmente, una serie
f()z)=a0.. J.. ()z)+2⋅ ⋅ .. k=1JUEGO JUEGO ak.. J.. +k()z){displaystyle f(z)=a_{0}{nu }J_{nu }(z)+2cdot sum _{k=1}^{infty ¿Qué? - Sí.

ak0=12π π i∫ ∫ SilenciozSilencio=cf()z)Ok()z)dz{displaystyle a_{k}{0}={frac {1}{2pi i}int _{ habitz habit=c}f(z)O_{k}(z),dz}

Las funciones seleccionadas admiten la representación especial
f()z)=.. k=0JUEGO JUEGO ak.. J.. +2k()z){displaystyle f(z)=sum ¿Qué? ¿Qué? +2k}(z)}

ak.. =2().. +2k)∫ ∫ 0JUEGO JUEGO f()z)J.. +2k()z)zdz{displaystyle a_{k}{nu }=2(nu +2k)int _{0}{infty }f(z){frac {J_{nu +2k}{z},dz}

∫ ∫ 0JUEGO JUEGO Jα α ()z)Jβ β ()z)dzz=2π π pecado ()π π 2()α α − − β β ))α α 2− − β β 2{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft} {f} {fnMicroc} {fnMicroc {2} {fnMicroc {f} {fnMicroc {f} {fnMicroc} {fnMicrosoft}} {f}} {f}}}} {f}f}}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnKf}fnKf}fnKf}f}f} {f}f}f}f}f}f}}fnKfnKf}fnKf}f}f}f}f}fn

Más generalmente, si f tiene un punto de bifurcación cerca del origen de tal naturaleza que
f()z)=.. k=0akJ.. +k()z){displaystyle f(z)=sum ¿Qué? - Sí.

L{}.. k=0akJ.. +k}()s)=11+s2.. k=0ak()s+1+s2).. +k{displaystyle {fnMithcal {fnh}fnh}fnfnh}ccH00}ccH00cH00cH00cH00cH00cH33} ¿Por qué? {1+s^{2}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {1+s^{2}}derecha) #

.. k=0ak.. .. +k=1+.. 22.. L{}f}()1− − .. 22.. ){displaystyle sum _{k=0}a_{k}xi ^{nu +k}={frac {1+xi ^{2}{2xi {fnMicroc {1-xi ^{2}{2xi }}right)}

 f
fOtra forma de definir las funciones de Bessel es la fórmula de representación de Poisson y la fórmula de Mehler-Sonine:
J.. ()z)=()z2).. .. ().. +12)π π ∫ ∫ − − 11eizs()1− − s2).. − − 12ds=2()z2).. ⋅ ⋅ π π ⋅ ⋅ .. ()12− − .. )∫ ∫ 1JUEGO JUEGO pecado zu()u2− − 1).. +12du{displaystyle {begin{aligned}J_{nu } {fnunció={frac {left {frac {fnMicroc}{2}}right)}{nu {fnMicrosoft Sans Serif} {fnMicroc {1}}right){sqrt {pi}}}int ¿Qué? {fnMicrosoft Sans Serif} {fnMicroc {2}},ds\[5px] {fnMicroc {2}{left({frac {2}}right)}{nu}{nu)}{nu)}{n0}{n0}{fn0}}}}}}s}s}s}}}}}}}s}s}}}}}}}}}}s}s}}}}s}}s}}s}s}sssssss}s}s}s}s}}s}s}}}}s}sssssssssssssssssssssssssssssss}ss.. "Gamma left" {frac {2}-nu right)}int _{1}^{infty }{frac {sin zu}{left(u^{2}-1right)^{nu +{2}}}}}}}}},duend{aligned}}}}}}}}}}}} {
![{displaystyle {begin{aligned}J_{nu }(z)&={frac {left({frac {z}{2}}right)^{nu }}{Gamma left(nu +{frac {1}{2}}right){sqrt {pi }}}}int _{-1}^{1}e^{izs}left(1-s^{2}right)^{nu -{frac {1}{2}}},ds\[5px]&={frac {2}{{left({frac {z}{2}}right)}^{nu }cdot {sqrt {pi }}cdot Gamma left({frac {1}{2}}-nu right)}}int _{1}^{infty }{frac {sin zu}{left(u^{2}-1right)^{nu +{frac {1}{2}}}}},duend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
Debido a que la ecuación de Bessel se vuelve hermitiana (autoadjunta) si se divide por x, las soluciones deben satisfacer una relación de ortogonalidad para las condiciones de contorno apropiadas. En particular, se sigue que:
∫ ∫ 01xJα α ()xuα α ,m)Jα α ()xuα α ,n)dx=δ δ m,n2[Jα α +1()uα α ,m)]2=δ δ m,n2[Jα α .()uα α ,m)]2{displaystyle int ¿Por qué? ¿Qué? ######left(u_{alpham}right)right]# {2}={\ frac {delta ¿Por qué?
![{displaystyle int _{0}^{1}xJ_{alpha }left(xu_{alpham}right)J_{alpha }left(xu_{alphan}right),dx={frac {delta _{m,n}}{2}}left[J_{alpha +1}left(u_{alpham}right)right]^{2}={frac {delta _{m,n}}{2}}left[J_{alpha }'left(u_{alpham}right)right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
Sigue inmediatamente una relación análoga para las funciones esféricas de Bessel:
∫ ∫ 01x2jα α ()xuα α ,m)jα α ()xuα α ,n)dx=δ δ m,n2[jα α +1()uα α ,m)]2{displaystyle int ¿Por qué? ¿Qué? ##################left(u_{alpham}right)right]
![{displaystyle int _{0}^{1}x^{2}j_{alpha }left(xu_{alpham}right)j_{alpha }left(xu_{alphan}right),dx={frac {delta _{m,n}}{2}}left[j_{alpha +1}left(u_{alpham}right)right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)
Si uno define una función boxcar de x que depende de un pequeño parámetro ε como:
fε ε ()x)=ε ε rectificado ()x− − 1ε ε ){displaystyle f_{varepsilon }(x)=varepsilon operatorname {rect} left({frac {x-1}{varepsilon }right)}

∫ ∫ 0JUEGO JUEGO kJα α ()kx)gε ε ()k)dk=fε ε ()x){displaystyle int _{0}{infty }kJ_{alpha }(kx)g_{varepsilon }(k),dk=f_{varepsilon }(x)}

∫ ∫ 0JUEGO JUEGO kJα α ()kx)Jα α ()k)dk=δ δ ()x− − 1){displaystyle int _{0}{infty }kJ_{alpha }(kx)J_{alpha }(k),dk=delta (x-1)}

Un cambio de variables produce la ecuación de cierre:
∫ ∫ 0JUEGO JUEGO xJα α ()ux)Jα α ()vx)dx=1uδ δ ()u− − v){displaystyle int _{0}{infty }xJ_{alpha }(ux)J_{alpha }(vx),dx={frac {1}{u}delta (u-v)}

∫ ∫ 0JUEGO JUEGO x2jα α ()ux)jα α ()vx)dx=π π 2u2δ δ ()u− − v){displaystyle int ¿Por qué? ¿Qué?

Otra propiedad importante de las ecuaciones de Bessel, que se deriva de la identidad de Abel, implica el Wronskiano de las soluciones:
Aα α ()x)dBα α dx− − dAα α dxBα α ()x)=Cα α x{displaystyle A_{alpha }(x){frac {fnMicrosoft Sans Serif} }{dx}-{frac {fnMicrosoft Sans Serif} }{dx}B_{alpha }(x)={frac {C_{alpha } {x}}

Jα α ()x)dYα α dx− − dJα α dxYα α ()x)=2π π x{displaystyle J_{alpha }(x){frac {fnMicrosoft Sans Serif} }{dx}-{frac {dJ_{\fnMicrosoft} } {dx}}Y_{alpha }(x)={frac {2}{pi x}}

Iα α ()x)dKα α dx− − dIα α dxKα α ()x)=− − 1x,{displaystyle I_{alpha }(x){frac {dK_{f}alfa }{dx}-{frac {dI_{i}alfa } {dx}K_{alpha }(x)=-{frac {1}{x}}

Para α > −1, la función entera par del género 1, x−α Jα(x), solo tiene ceros reales. Dejar
<math alttext="{displaystyle 0<j_{alpha1}<j_{alpha2}<cdots <j_{alphan}0.jα α ,1.jα α ,2.⋯ ⋯ .jα α ,n.⋯ ⋯ {fnMicrosoft Sans Serif} {cdots {cdots} {cdots} {cdots} {cdots}
<img alt="{displaystyle 0<j_{alpha1}<j_{alpha2}<cdots <j_{alphan}
Jα α ()z)=()z2)α α .. ()α α +1)∏ ∏ n=1JUEGO JUEGO ()1− − z2jα α ,n2){displaystyle J_{alpha }(z)={frac {left({frac {frac}{2}}right)}{alpha }{Gamma (alpha +1)}prod ¿Qué? {Z^{2}{j_{alphan} {2}}right)}

(Hay una gran cantidad de otras integrales e identidades conocidas que no se reproducen aquí, pero que se pueden encontrar en las referencias).
Relaciones de recurrencia
Las funciones Jα, Yα, H(1)
α y H(2)
α todos satisfacen las relaciones de recurrencia
2α α xZα α ()x)=Zα α − − 1()x)+Zα α +1()x){displaystyle {frac {22alpha }Z_{alpha }(x)=Z_{alpha -1}(x)+Z_{alpha +1}(x)}

2dZα α ()x)dx=Zα α − − 1()x)− − Zα α +1()x),{displaystyle 2{frac {dZ_{alpha } {x}}=Z_{alpha -1}(x)-Z_{alpha +1}(x),}

()1xddx)m[xα α Zα α ()x)]=xα α − − mZα α − − m()x),()1xddx)m[Zα α ()x)xα α ]=()− − 1)mZα α +m()x)xα α +m.{fnK} {fnMicroc {} {f} {fnMicroc {} {fnMicroc {d}dx}right)}m}left[x^{alpha }Z_{alpha }(x)right] {fnMicrosoft Sans Serif} {fnK} {fnMicroc} {fnMicroc {} {f}}}derecho)} {m} {fnMicroc {fnMicrosoft} {fnunci} {ccccH00} {cH00}}} {c}ccccc}}}cccccH00}cccc} {cH00}cccccH00}ccccccH00}cccccccccccccccccH00}ccH00}ccc}cH00}cH00}ccH00}ccH00}ccH00}c}c}c {fnK}}
![{displaystyle {begin{aligned}left({frac {1}{x}}{frac {d}{dx}}right)^{m}left[x^{alpha }Z_{alpha }(x)right]&=x^{alpha -m}Z_{alpha -m}(x),\left({frac {1}{x}}{frac {d}{dx}}right)^{m}left[{frac {Z_{alpha }(x)}{x^{alpha }}}right]&=(-1)^{m}{frac {Z_{alpha +m}(x)}{x^{alpha +m}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)
Las funciones
Modified de Bessel siguen relaciones similares:
e()x2)()t+1t)=.. n=− − JUEGO JUEGO JUEGO JUEGO In()x)tn{displaystyle e^{left({frac {x}{2}right)left(t+{frac {1}{t}right)}=sum ¿Qué?

ez# Silencio Silencio =I0()z)+2.. n=1JUEGO JUEGO In()z)# nSilencio Silencio {displaystyle e^{zcos theta }=I_{0}(z)+2sum _{n=1} {infty }I_{n}(z)cos ntheta }

12π π ∫ ∫ 02π π ez# ()mSilencio Silencio )+Sí.# Silencio Silencio dSilencio Silencio =I0()z)I0()Sí.)+2.. n=1JUEGO JUEGO In()z)Imn()Sí.).{displaystyle {frac {1}{2pi}int _{0}{2pi}e^{zcos(mtheta)+ycos theta }dtheta =I_{0}(z)I_{0}(y)+2sum _{n=1}{infty }I_{n}(z)I_{mn}(y). }

La relación de recurrencia dice
Cα α − − 1()x)− − Cα α +1()x)=2α α xCα α ()x),Cα α − − 1()x)+Cα α +1()x)=2dCα α ()x)dx,{displaystyle {begin{aligned}C_{alpha -1}(x)-C_{alpha +1}(x) implica={frac {2alpha } {x}C_{alpha }(x),C_{alpha -1}(x)+C_{alpha +1}(x) correspond=2{frac {dC_{alpha }(x)}{dx}}}end{aligned}}}

Trascendencia
En 1929, Carl Ludwig Siegel demostró que Jν(x), J' ν(x), y el cociente J'ν(x)/Jν(x) son números trascendentales cuando ν es racional y x es algebraico y distinto de cero. La misma prueba también implica que Kν(x) es trascendental bajo los mismos supuestos.
Teorema de la multiplicación
Las funciones de Bessel obedecen a un teorema de la multiplicación
λ λ − − .. J.. ()λ λ z)=.. n=0JUEGO JUEGO 1n!()()1− − λ λ 2)z2)nJ.. +n()z),{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fn} {fn} {fn} {fn}fn}}left {left {left(1-lambda ^{2}right)}{2}n}{n}n}n}}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}nn}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n}n

λ λ − − .. I.. ()λ λ z)=.. n=0JUEGO JUEGO 1n!()()λ λ 2− − 1)z2)nI.. +n()z){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fn} {fn} {fn}fn}fnfn} {fn} {fnK}fn}fnhn}fn}fnhnhnhnhn}fnhn}fnhnhnhnhnhnhn}fn}fnhnh]fnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhn}fnhnhnhn}hnhnhn}hnhnhn}hnhn}hnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhnhn}hnhnhn

λ λ − − .. K.. ()λ λ z)=.. n=0JUEGO JUEGO ()− − 1)nn!()()λ λ 2− − 1)z2)nK.. +n()z).{fnMicrosoft Sans Serif} {fnn} {fnfnn}}nnn}nnn} {fn} {fn} {fn}}nnnnn}nnnn}m} {n}nK}n}nKnKnKn}nKnKnKnKn}nKnKn}}nKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnKnK - Sí.

Ceros de la función de Bessel
La hipótesis de Bourget
El mismo Bessel demostró originalmente que para enteros no negativos n, la ecuación J n(x) = 0 tiene un número infinito de soluciones en x. Cuando se grafican las funciones Jn(x) en el mismo gráfico, sin embargo, ninguno de los ceros parece coincidir para diferentes valores de n excepto por el cero en x = 0. Este fenómeno se conoce como hipótesis de Bourget en honor al matemático francés del siglo XIX que estudió las funciones de Bessel. Específicamente establece que para cualquier número entero n ≥ 0 y m ≥ 1, las funciones Jn(x) y Jn + m(x) no tienen ceros comunes que no sean el de x = 0. La hipótesis fue probada por Carl Ludwig Siegel en 1929.
Trascendencia
Siegel demostró en 1929 que cuando . es racional, todas las raíces no cero de J.x) y J'.x) son trascendental, como todas las raíces K.x). También se sabe que todas las raíces de los derivados superiores J.. ()n)()x){displaystyle J_{nu }{(n)}(x)} para n≤ 18 son trascendental, excepto para los valores especiales J1()3)()± ± 3)=0{displaystyle J_{1} {pm {sqrt {3}}=0}
para n≤ 18 son trascendental, excepto para los valores especiales J1()3)()± ± 3)=0{displaystyle J_{1} {pm {sqrt {3}}=0} y J0()4)()± ± 3)=0{displaystyle J_{0} {pm {sqrt {3}}=0}
y J0()4)()± ± 3)=0{displaystyle J_{0} {pm {sqrt {3}}=0} .
.
Enfoques numéricos
Para estudios numéricos sobre los ceros de la función de Bessel, véase Gil, Segura & Temme (2007), Kravanja et al. (1998) y Moler (2004).
Valores numéricos
El primer cero en J0 (es decir, j0,1, j0,2 y j0,3 ) ocurre en argumentos de aproximadamente 2.40483, 5.52008 y 8.65373, respectivamente.
Más resultados...
0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/> Donde Jα α ()x){displaystyle J_{alpha }(x)}, Yα α ()x){displaystyle Y_{alpha }(x)} son reales, las funciones Bessel de primer y segundo tipo son las partes reales e imaginarias, respectivamente, de la primera función Hankel y las partes imaginarias reales y negativas de la segunda función Hankel. Así, las fórmulas anteriores son análogos de la fórmula de Euler, sustituyendo H1)








































































![{displaystyle {begin{aligned}I_{alpha }(z)={frac {1}{{sqrt {2pi z}}{sqrt[{4}]{1+{frac {alpha ^{2}}{z^{2}}}}}}}exp left(-alpha operatorname {arsinh} left({frac {alpha }{z}}right)+z{sqrt {1+{frac {alpha ^{2}}{z^{2}}}}}right)left(1+{mathcal {O}}left({frac {1}{z{sqrt {1+{frac {alpha ^{2}}{z^{2}}}}}}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f57e4803db262b5efdc20c32da3835c3fd4f0f9d)













![{displaystyle {begin{aligned}J_{nu }(z)&={frac {left({frac {z}{2}}right)^{nu }}{Gamma left(nu +{frac {1}{2}}right){sqrt {pi }}}}int _{-1}^{1}e^{izs}left(1-s^{2}right)^{nu -{frac {1}{2}}},ds\[5px]&={frac {2}{{left({frac {z}{2}}right)}^{nu }cdot {sqrt {pi }}cdot Gamma left({frac {1}{2}}-nu right)}}int _{1}^{infty }{frac {sin zu}{left(u^{2}-1right)^{nu +{frac {1}{2}}}}},duend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
![{displaystyle int _{0}^{1}xJ_{alpha }left(xu_{alpham}right)J_{alpha }left(xu_{alphan}right),dx={frac {delta _{m,n}}{2}}left[J_{alpha +1}left(u_{alpham}right)right]^{2}={frac {delta _{m,n}}{2}}left[J_{alpha }'left(u_{alpham}right)right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
![{displaystyle int _{0}^{1}x^{2}j_{alpha }left(xu_{alpham}right)j_{alpha }left(xu_{alphan}right),dx={frac {delta _{m,n}}{2}}left[j_{alpha +1}left(u_{alpham}right)right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)











![{displaystyle {begin{aligned}left({frac {1}{x}}{frac {d}{dx}}right)^{m}left[x^{alpha }Z_{alpha }(x)right]&=x^{alpha -m}Z_{alpha -m}(x),\left({frac {1}{x}}{frac {d}{dx}}right)^{m}left[{frac {Z_{alpha }(x)}{x^{alpha }}}right]&=(-1)^{m}{frac {Z_{alpha +m}(x)}{x^{alpha +m}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)









