Exponente de Lyapunov

Explicaciones del exponente de Lyapunov

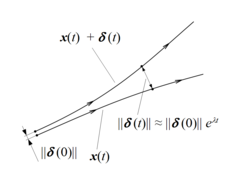
En matemáticas, la Lyapunov exponent o Liapunov característico exponente de un sistema dinámico es una cantidad que caracteriza la tasa de separación de trayectorias infinitamente cercanas. Cuantitativamente, dos trayectorias en espacio de fase con vector de separación inicial ${displaystyle delta mathbf {Z}$ divergencia (siempre que la divergencia puede ser tratada dentro de la aproximación linealizada) a una tasa dada por

${displaystyle Нdelta mathbf {Z} (t) persistenciaapprox e^{lambda t} eternadelta mathbf [Z] _{0}$

Donde ${displaystyle lambda }$ es el exponente de Lyapunov.

La tasa de separación puede ser diferente para diferentes orientaciones del vector de separación inicial. Por lo tanto, hay un espectro de exponentes de Lyapunov, igual en número a la dimensionalidad del espacio de fase. Es común referirse al mayor como el máximo exponente de Lyapunov (MLE), porque determina una noción de previsibilidad para un sistema dinámico. Un MLE positivo generalmente se toma como una indicación de que el sistema es caótico (siempre que se cumplan algunas otras condiciones, por ejemplo, la compacidad del espacio de fase). Tenga en cuenta que un vector de separación inicial arbitrario normalmente contendrá algún componente en la dirección asociada con el MLE y, debido a la tasa de crecimiento exponencial, el efecto de los otros exponentes se borrará con el tiempo.

El exponente lleva el nombre de Aleksandr Lyapunov.

Definición del exponente máximo de Lyapunov

El exponente máximo de Lyapunov se puede definir de la siguiente manera:

${displaystyle lambda =lim _{tto infty }lim _{ vidasdelta mathbf {Z} _{0} Anteriorto 0}{frac {1}{t}}ln {frac {deltamathbf {Z} (t) [Z] _{0}$

El límite ${fnMicrosoft Sans Serif} _{0} 0}$ garantiza la validez de la aproximación lineal en cualquier momento.

Para sistema de tiempo discreto (mapas o iteraciones de puntos fijos) ${displaystyle x_{n+1}=f(x_{n}}$para una órbita comenzando con ${displaystyle x_{0}$ esto se traduce en:

${displaystyle lambda (x_{0})=lim _{nto infty }{frac {1}{n}}sum ¿Por qué?$

Definición del espectro de Lyapunov

El vector líder de Lyapunov.

Para un sistema dinámico con ecuación de evolución ${displaystyle {dot {x}_{i}=f_{i}(x)}$ en una n– espacio de fase dimensional, el espectro de los exponentes de Lyapunov

${displaystyle {lambda _{1},lambda _{2},ldotslambda ¿Qué?$

en general, depende del punto de partida ${displaystyle x_{0}$. Sin embargo, por lo general nos interesará el receptor (o los atractores) de un sistema dinámico, y normalmente habrá un conjunto de exponentes asociados con cada accionista. La elección del punto de partida puede determinar cuál atracción el sistema termina en, si hay más de uno. (Para los sistemas Hamiltonianos, que no tienen atracción, esto no es una preocupación.) Los exponentes de Lyapunov describen el comportamiento de los vectores en el espacio tangente del espacio de fase y se definen de la matriz jacobina

${displaystyle J_{ij}(t)=left.{frac {df_{i}{dx_{j}}}}right imper_{x(t)}}$

este Jacobiano define la evolución de los vectores tangentes, dada por la matriz ${displaystyle Sí.$, a través de la ecuación

${displaystyle { dot {}=JY}$

con la condición inicial ${displaystyle Y_{ij}(0)=delta ¿Qué?$. La matriz ${displaystyle Sí.$ describe cómo un pequeño cambio en el punto ${displaystyle x(0)}$ se propaga al punto final ${displaystyle x(t)}$. El límite

${displaystyle Lambda =lim _{trightarrow infty }{frac {1}{2t}log(Y(t)Y^{T}(t)}}$

define una matriz ${displaystyle Lambda }$ (las condiciones para la existencia del límite son dadas por el teorema de Oseledets). Los exponentes de Lyapunov ${displaystyle lambda _{i}$ son definidos por los eigenvalues de ${displaystyle Lambda }$.

El conjunto de exponentes de Lyapunov será el mismo para casi todos los puntos de partida de un componente ergódico del sistema dinámico.

Exponente de Lyapunov para linealización variable en el tiempo

Para presentar a Lyapunov exponent considerar una matriz fundamental ${displaystyle X(t)}$(por ejemplo, para la linealización a lo largo de una solución estacionaria ${displaystyle x_{0}$ en un sistema continuo, la matriz fundamental es ${displaystyle exp left(left.{frac {df^{t}{dx}}right sobre la vida_{x_{0}tright)}$consistente en soluciones linealmente independientes de la aproximación de primer orden del sistema. Los valores singulares ${displaystyle {alpha _{j}{big (}X(t){big)}}_{1}{n}} {}}$de la matriz ${displaystyle X(t)}$ son las raíces cuadradas de los eigenvalues de la matriz ${displaystyle X(t)^{*}X(t)}$. El mayor exponente de Lyapunov ${displaystyle lambda _{mathrm {max}}$ como sigue:

${displaystyle lambda _{mathrm {max}=max limits _{j}limsup _{trightarrow infty {1} {t}ln alpha _{j}{big (}X(t){big)}}$

A.M. Lyapunov demostró que si el sistema de la primera aproximación es regular (por ejemplo, todos los sistemas con coeficientes constantes y periódicos son regulares) y su mayor exponente de Lyapunov es negativo, entonces la solución del sistema original es asintóticamente estable en Lyapunov. Más tarde, O. Perron afirmó que el requisito de regularidad de la primera aproximación es sustancial.

Efectos Perron de la mayor inversión de signo del exponente de Lyapunov

En 1930 O. Perron construyó un ejemplo de un sistema de segundo orden, donde la primera aproximación tiene exponentes de Lyapunov negativos a lo largo de una solución cero del sistema original pero, al mismo tiempo, esta solución cero del sistema no lineal original es Lyapunov inestable. Además, en cierta vecindad de esta solución cero, casi todas las soluciones del sistema original tienen exponentes de Lyapunov positivos. Además, es posible construir un ejemplo inverso en el que la primera aproximación tiene exponentes de Lyapunov positivos a lo largo de una solución cero del sistema original pero, al mismo tiempo, esta solución cero del sistema no lineal original es Lyapunov estable. El efecto de inversión de signo de los exponentes de Lyapunov de soluciones del sistema original y el sistema de primera aproximación con los mismos datos iniciales fue posteriormente llamado efecto Perron.

El contraejemplo de Perron muestra que un exponente de Lyapunov negativo mayor no indica, en general, estabilidad, y que un máximo exponente positivo de Lyapunov, en general, no indica caos.

Por lo tanto, la linealización variable en el tiempo requiere una justificación adicional.

Propiedades básicas

Si el sistema es conservador (es decir, no hay disipación), un elemento de volumen del espacio de fase permanecerá igual a lo largo de una trayectoria. Por tanto, la suma de todos los exponentes de Lyapunov debe ser cero. Si el sistema es disipativo, la suma de los exponentes de Lyapunov es negativa.

Si el sistema es un flujo y la trayectoria no converge en un solo punto, un exponente es siempre cero—el exponente de Lyapunov correspondiente al valor eigenvalue de ${displaystyle L.$ con un eigenvector en la dirección del flujo.

Importancia del espectro de Lyapunov

El espectro de Lyapunov se puede utilizar para dar una estimación de la tasa de producción de entropía, de la dimensión fractal, y de la dimensión Hausdorff del sistema dinámico considerado. En particular del conocimiento del espectro de Lyapunov es posible obtener el llamado Dimensión Lyapunov (o dimensión Kaplan–Yorke) ${displaystyle D_{KY}$, que se define como sigue:

${displaystyle D_{KY}=k+sum ¿Por qué? {fnMicrode ¿Qué? ¿Qué?$

Donde ${displaystyle k}$ es el entero máximo tal que la suma de la ${displaystyle k}$ exponentes más grandes todavía no es negativo. ${displaystyle D_{KY}$ representa un límite superior para la dimensión de información del sistema. Además, la suma de todos los exponentes positivos de Lyapunov da una estimación de la entropía Kolmogorov-Sinai en consecuencia al teorema de Pesin. Junto con métodos numéricos ampliamente utilizados para estimar y computar la dimensión Lyapunov hay un enfoque analítico eficaz, que se basa en el método Lyapunov directo con funciones especiales de Lyapunov. Los exponentes de Lyapunov de trayectoria atada y la dimensión de Lyapunov de la atracción son invariantes bajo la difusión del espacio de fase.

El inverso multiplicativo del mayor exponente de Lyapunov se denomina a veces en la literatura como tiempo de Lyapunov, y define el tiempo característico de plegado e. Para órbitas caóticas, el tiempo de Lyapunov será finito, mientras que para órbitas regulares será infinito.

Cálculo numérico

Puntos dentro y fuera Mandelbrot conjunto coloreado por Lyapunov exponent.

Generalmente el cálculo de los exponentes de Lyapunov, tal como se define anteriormente, no se puede llevar a cabo analíticamente, y en la mayoría de los casos se debe recurrir a técnicas numéricas. An early example, which also constituted the first demonstration of the exponential divergence of chaotic pathctories, was carried out by R. H. Miller in 1964. Actualmente, el procedimiento numérico más utilizado estima el ${displaystyle L.$ matriz basada en el promedio de varias aproximaciones de tiempo finito del límite que define ${displaystyle L.$.

Una de las técnicas numéricas más utilizadas y efectivas para calcular el espectro de Lyapunov para un sistema dinámico uniforme se basa en Ortonormalización de Gram-Schmidt de los vectores de Lyapunov para evitar una desalineación de todos los vectores a lo largo de la dirección de máxima expansión. Se describe el espectro de Lyapunov de varios modelos. Se introducen los códigos fuente para el mapa de Hénon, las ecuaciones de Lorenz y algunas ecuaciones diferenciales de retardo.

Para el cálculo de los exponentes de Lyapunov a partir de datos experimentales limitados, se han propuesto varios métodos. Sin embargo, existen muchas dificultades con la aplicación de estos métodos y estos problemas deben abordarse con cuidado. La principal dificultad es que los datos no exploran completamente el espacio de fase, sino que se limitan al atractor que tiene una extensión muy limitada (si la tiene) en ciertas direcciones. Estas direcciones más delgadas o más singulares dentro del conjunto de datos son las asociadas con los exponentes más negativos. Se ha demostrado que el uso de mapeos no lineales para modelar la evolución de pequeños desplazamientos del atractor mejora drásticamente la capacidad de recuperar el espectro de Lyapunov, siempre que los datos tengan un nivel de ruido muy bajo. También se ha explorado la naturaleza singular de los datos y su conexión con los exponentes más negativos.

Exponente local de Lyapunov

Mientras que el exponente (global) de Lyapunov da una medida de la previsibilidad total de un sistema, a veces es interesante estimar la previsibilidad local alrededor de un punto x₀ en el espacio de fase. Esto se puede hacer a través de los valores propios de la matriz jacobiana J ⁰(x₀). Estos valores propios también se denominan exponentes locales de Lyapunov. (Una palabra de precaución: a diferencia de los exponentes globales, estos exponentes locales no son invariantes bajo un cambio de coordenadas no lineal).

Exponente condicional de Lyapunov

Este término se usa normalmente con respecto a la sincronización del caos, en la que hay dos sistemas que se acoplan, generalmente de manera unidireccional, de modo que hay un sistema de accionamiento (o maestro) y un sistema de respuesta (o esclavo). Los exponentes condicionales son los del sistema de respuesta con el sistema impulsor tratado simplemente como la fuente de una señal impulsora (caótica). La sincronización ocurre cuando todos los exponentes condicionales son negativos.