Escala (mapa)
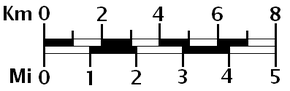

El escala de un mapa es la relación de una distancia en el mapa a la distancia correspondiente en el suelo. Este concepto simple es complicado por la curvatura de la superficie de la Tierra, que obliga a variar a través de un mapa. Debido a esta variación, el concepto de escala se vuelve significativo en dos formas distintas.
La primera es la relación del tamaño del generador de globo al tamaño de la Tierra. El globo generador es un modelo conceptual al que la Tierra está arrugada y del que se proyecta el mapa. La relación del tamaño de la Tierra con el tamaño del globo generador se llama el Escala nominal (también llamado escala principal o fracción representativa). Muchos mapas indican la escala nominal e incluso pueden mostrar una escala de barras (a veces simplemente llamada "escala") para representarla.
El segundo concepto distinto de escala se aplica a la variación de escala en un mapa. Es la relación entre la escala del punto mapeado y la escala nominal. En este caso, la 'escala' significa el factor de escala (también llamado escala de puntos o escala particular).
Si la región del mapa es lo suficientemente pequeña para ignorar la curvatura de la Tierra, como en un plan de la ciudad, entonces se puede utilizar un solo valor como la escala sin causar errores de medición. En mapas que cubren áreas más grandes, o toda la Tierra, la escala del mapa puede ser menos útil o incluso inútil en la medición de distancias. La proyección del mapa se vuelve crítica para entender cómo la escala varía a lo largo del mapa. Cuando la escala varía notablemente, se puede considerar como el factor de escala. La indicatrix de Tissot se utiliza a menudo para ilustrar la variación de la escala de puntos a través de un mapa.
Historia
Los fundamentos de la escala cuantitativa de los mapas se remontan a la antigua China con evidencia textual de que la idea de la escala de los mapas se entendió en el siglo II a.C. Los antiguos topógrafos y cartógrafos chinos utilizaban amplios recursos técnicos para producir mapas, como varillas para contar, escuadras de carpintero, plomadas, compases para dibujar círculos y tubos de observación para medir la inclinación. Los antiguos astrónomos chinos insinuaron marcos de referencia que postulaban un sistema de coordenadas naciente para identificar ubicaciones que dividieron el cielo en varios sectores o logias lunares.
El cartógrafo y geógrafo chino Pei Xiu del período de los Tres Reinos creó un conjunto de mapas de grandes áreas dibujados a escala. Produjo un conjunto de principios que enfatizaban la importancia de una escala consistente, mediciones direccionales y ajustes en las mediciones terrestres en el terreno que se estaba cartografiando.
Terminología
Representación de escala
Las escalas de mapas se pueden expresar en palabras (una escala léxica), como una proporción o como una fracción. Ejemplos son:
- "un centímetro a cien metros" o 1:10.000 o 1/10.000
- 'una pulgada a una milla' o 1:63,360 o 1/63,360
- "un centímetro a mil kilómetros" o 1.100.000 o 1/100.000.000. (La proporción normalmente se abreviaría a 1:100M)
Escala de barras versus escala léxica
Además de los mapas arriba muchos llevan uno o más (gráfico) bar escalas. Por ejemplo, algunos mapas británicos modernos tienen tres escalas de barras, una para kilómetros, millas y millas náuticas.
Una escala lexical en un idioma conocido por el usuario puede ser más fácil de visualizar que una relación: si la escala es de una pulgada a dos millas y el usuario del mapa puede ver dos aldeas que están a unos dos pulgadas de distancia en el mapa, entonces es fácil averiguar que los pueblos están a unos cuatro millas de distancia en el suelo.
Una escala léxica puede causar problemas si se expresa en un idioma que el usuario no comprende o en unidades obsoletas o mal definidas. Por ejemplo, muchas personas mayores en países donde las unidades imperiales solían enseñarse en las escuelas entenderán una escala de una pulgada a un estadio (1:7920). Pero una escala de una libra a una legua puede ser aproximadamente 1:144.000, dependiendo de la elección del cartógrafo entre las muchas definiciones posibles para una legua, y sólo una minoría de los usuarios modernos estará familiarizado con las unidades utilizadas.
Gran escala, mediana escala, pequeña escala
- Contraste a escala espacial.
Un mapa de pequeña escala cubre grandes regiones, como mapas del mundo, continentes o naciones grandes. Es decir, muestran grandes extensiones de terreno en un espacio reducido. Se denominan de pequeña escala porque la fracción representativa es relativamente pequeña.
Los mapasa gran escala muestran áreas más pequeñas con más detalle, como podrían hacerlo los mapas de condado o los planos urbanos. Estos mapas se denominan de gran escala porque la fracción representativa es relativamente grande. Por ejemplo, un plano urbano, que es un mapa a gran escala, podría estar en una escala de 1:10.000, mientras que el mapa mundial, que es un mapa a pequeña escala, podría estar en una escala de 1:100.000.000.
La siguiente tabla describe los rangos típicos de estas escalas, pero no debe considerarse autorizada porque no existe un estándar:
| Clasificación | Rango | Ejemplos |
|---|---|---|
| gran escala | 1:0 – 1:600,000 | 1:0.00001 para el mapa del virus; 1:5.000 para el mapa de la ciudad |
| escala media | 1:600,000 – 1:2,000,000 | Mapa de un país |
| pequeña escala | 1:2,000,000 – 1: | 1:50,000,000 para mapa mundial; 1:1021 para mapa de galaxia |
Los términos a veces se utilizan en el sentido absoluto de la tabla, pero otras veces en un sentido relativo. Por ejemplo, un lector de mapas cuyo trabajo se refiere únicamente a mapas de gran escala (como se tabuló anteriormente) podría referirse a un mapa en 1:500.000 como de pequeña escala.
En el idioma inglés, la palabra "gran escala" se utiliza a menudo para significar "extenso". Sin embargo, como se explicó anteriormente, los cartógrafos utilizan el término "gran escala" para referirse a mapas menos extensos, aquellos que muestran un área más pequeña. Los mapas que muestran un área extensa son mapas de "pequeña escala" mapas. Esto puede ser motivo de confusión.
Variación de escala
El mapeo de áreas grandes causa distorsiones notables porque aplana significativamente la superficie curva de la tierra. La forma en que se distribuye la distorsión depende de la proyección del mapa. La escala varía en todo el mapa y la escala del mapa indicada es solo una aproximación. Esto se analiza en detalle a continuación.
Mapas a gran escala con curvatura descuidada
La región en la que la Tierra puede considerarse plana depende de la precisión de las mediciones topográficas. Si se mide sólo al metro más cercano, la curvatura de la Tierra es indetectable en una distancia meridiana de unos 100 kilómetros (62 millas) y en una línea este-oeste de unos 80 km (a una latitud de 45 grados). Si se mide con una precisión de 1 milímetro (0,039 pulgadas), la curvatura es indetectable en una distancia de meridiano de aproximadamente 10 km y en una línea este-oeste de aproximadamente 8 km. Por lo tanto, un plano de la ciudad de Nueva York con una precisión de un metro o un plano del sitio de construcción con una precisión de un milímetro satisfarían las condiciones anteriores para despreciar la curvatura. Pueden tratarse mediante topografía plana y cartografiarse mediante dibujos a escala en los que dos puntos cualesquiera a la misma distancia en el dibujo estén a la misma distancia en el suelo. Las distancias terrestres reales se calculan midiendo la distancia en el mapa y luego multiplicándola por la inversa de la fracción de escala o, de manera equivalente, simplemente usando divisores para transferir la separación entre los puntos en el mapa a una escala de barras en el mapa.
Escala de puntos (o escala particular)
Como lo demuestra el Teorema Egregium de Gauss, una esfera (o elipsoide) no se puede proyectar sobre un plano sin distorsión. Esto se ilustra comúnmente por la imposibilidad de alisar una cáscara de naranja sobre una superficie plana sin rasgarla ni deformarla. La única representación verdadera de una esfera a escala constante es otra esfera como un globo terráqueo.
Dado el tamaño práctico limitado de los globos, debemos utilizar mapas para realizar mapas detallados. Los mapas requieren proyecciones. Una proyección implica distorsión: una separación constante en el mapa no corresponde a una separación constante en el terreno. Si bien un mapa puede mostrar una escala de barra gráfica, la escala debe usarse con el entendimiento de que será precisa solo en algunas líneas del mapa. (Esto se analiza con más detalle en los ejemplos de las siguientes secciones).
Vamos. P ser un punto de latitud φ φ {displaystyle varphi } y longitud λ λ {displaystyle lambda } en la esfera (o ellipsoide). Dejar Q ser un punto vecino y dejar α α {displaystyle alpha } ser el ángulo entre el elemento PQ y el meridiano en P: este ángulo es el azimuth ángulo del elemento PQ. Dejemos que P' y Q' sean puntos correspondientes en la proyección. El ángulo entre la dirección P'Q' y la proyección del meridiano es el rodamientos β β {displaystyle beta }. En general α α ل ل β β {displaystyle alpha neq beta }. Comentario: esta distinción precisa entre azimut (en la superficie de la Tierra) y el rodamiento (en el mapa) no se observa universalmente, muchos escritores usando los términos casi intercambiables.
Definición: la escala de puntos en P es la relación de las dos distancias P'Q' y PQ en el límite en el que Q se aproxima a P. Escribimos esto como
- μ μ ()λ λ ,φ φ ,α α )=limQ→ → PP.Q.PQ,{displaystyle mu (lambda,varphialpha)=lim _{Qto P}{frac {P'Q'} {PQ}}
donde la notación indica que la escala de puntos es función de la posición de P y también de la dirección del elemento PQ.
Definición: si P y Q mienten en el mismo meridiano ()α α =0){displaystyle (alpha =0)}, el escala meridiana es denotado por h()λ λ ,φ φ ){displaystyle h(lambda,varphi)}.
Definición: si P y Q se encuentran en el mismo paralelo ()α α =π π /2){displaystyle (alpha =pi /2)}, el escala paralela es denotado por k()λ λ ,φ φ ){displaystyle k(lambda,varphi)}.
Definición: si la escala de puntos depende sólo de la posición, no de la dirección, decimos que es isotrópica y convencionalmente denota su valor en cualquier dirección por el factor de escala paralela k()λ λ ,φ φ ){displaystyle k(lambdavarphi)}.
Definición: Se dice que una proyección cartográfica es conforme si el ángulo entre un par de líneas que se cruzan en un punto P es el mismo que el ángulo entre las líneas proyectadas en el punto proyectado P'. ;, para todos los pares de líneas que se cruzan en el punto P. Un mapa conforme tiene un factor de escala isotrópico. Por el contrario, los factores de escala isotrópica en todo el mapa implican una proyección conforme.
La isotropía de escala implica que los elementos pequeños se estiran por igual en todas las direcciones, es decir, se conserva la forma de un elemento pequeño. Esta es la propiedad del ortomorfismo (del griego 'forma recta'). La calificación 'pequeña' significa que con una determinada precisión de medición no se puede detectar ningún cambio en el factor de escala sobre el elemento. Dado que las proyecciones conformes tienen un factor de escala isotrópico, también se les ha llamado proyecciones ortomórficas. Por ejemplo, la proyección de Mercator es conforme ya que está construida para preservar los ángulos y su factor de escala es isotrópico, una función de la latitud únicamente: Mercator conserva la forma en regiones pequeñas.
Definición: en una proyección conforme con una escala isotrópica, los puntos que tienen el mismo valor de escala se pueden unir para formar las líneas de isoescala. Estos no están trazados en mapas para usuarios finales, pero aparecen en muchos de los textos estándar. (Consulte Snyder, páginas 203 a 206).
La fracción representativa (RF) o escala principal
Hay dos convenciones que se utilizan para establecer las ecuaciones de cualquier proyección dada. Por ejemplo, la proyección cilíndrica equirectangular se puede escribir como
- cartógrafos: x=aλ λ {displaystyle x=alambda} Sí.=aφ φ {displaystyle y=avarphi }
- matemáticos: x=λ λ {displaystyle x=lambda} Sí.=φ φ {displaystyle y=varphi }
Aquí adoptaremos la primera de estas convenciones (siguiendo el uso en las encuestas de Snyder). Claramente, las ecuaciones de proyección anteriores definen posiciones en un enorme cilindro enrollado alrededor de la Tierra y luego desenrollado. Decimos que estas coordenadas definen el mapa de proyección que debe distinguirse lógicamente de los mapas impresos (o vistos) reales. Si la definición de escala de puntos en la sección anterior es en términos del mapa de proyección, entonces podemos esperar que los factores de escala estén cerca de la unidad. Para proyecciones cilíndricas tangentes normales, la escala a lo largo del ecuador es k=1 y, en general, la escala cambia a medida que nos alejamos del ecuador. El análisis de escala en el mapa de proyección es una investigación del cambio de k lejos de su verdadero valor de unidad.
Los mapas impresos reales se producen a partir del mapa de proyección mediante una escala constante denotada por una proporción como 1:100M (para mapas del mundo entero) o 1:10000 ( (por ejemplo, planos urbanos). Para evitar confusión en el uso de la palabra 'escala' esta constante La fracción de escala se llama fracción representativa (RF) del mapa impreso y debe identificarse con la proporción impresa en el mapa. Las coordenadas reales del mapa impreso para la proyección cilíndrica equirectangular son
- mapa impreso: x=()RF)aλ λ {displaystyle x=(RF)alambda } Sí.=()RF)aφ φ {displaystyle y=(RF)avarphi }
Esta convención permite una distinción clara entre la escala de proyección intrínseca y la escala de reducción.
A partir de este punto ignoramos la RF y trabajamos con el mapa de proyección.
Visualización de la escala de puntos: la indicatriz de Tissot

Considere un pequeño círculo sobre la superficie de la Tierra centrado en un punto P a la latitud φ φ {displaystyle varphi } y longitud λ λ {displaystyle lambda }. Puesto que la escala de puntos varía con posición y dirección, la proyección del círculo sobre la proyección será distorsionada. Tissot demostró que, mientras la distorsión no sea demasiado grande, el círculo se convertirá en un elipse en la proyección. En general la dimensión, forma y orientación de la elipse cambiará sobre la proyección. Superponer estos elips de distorsión en la proyección del mapa transmite la forma en que la escala de puntos está cambiando sobre el mapa. El elipse de la distorsión se conoce como indicatriz de Tissot. El ejemplo que se muestra aquí es la proyección de Winkel tripel, la proyección estándar de mapas mundiales hecha por la National Geographic Society. La distorsión mínima está en el meridiano central en latitudes de 30 grados (Norte y Sur). (Otros ejemplos).
Escala de puntos para proyecciones cilíndricas normales de la esfera
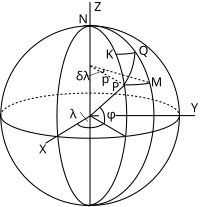
La llave de un cuantitativa cuantitativa cuantitativa entender la escala es considerar un elemento infinitesimal en la esfera. La figura muestra un punto P en latitud φ φ {displaystyle varphi } y longitud λ λ {displaystyle lambda } en la esfera. El punto Q está en latitud φ φ +δ δ φ φ {displaystyle varphi +delta varphi } y longitud λ λ +δ δ λ λ {displaystyle lambda +delta lambda }. Las líneas PK y MQ son arcos de meridianos de longitud aδ δ φ φ {displaystyle a,delta varphi } Donde a{displaystyle a} es el radio de la esfera y φ φ {displaystyle varphi } está en medida radiana. Las líneas PM y KQ son arcos de círculos paralelos de longitud ()a# φ φ )δ δ λ λ {displaystyle (acos varphi)delta lambda } conλ λ {displaystyle lambda } en medida radiana. Conducir un punto propiedad de la proyección a P basta tomar un elemento infinitesimal PMQK de la superficie: en el límite de Q acercarse P tal elemento tiende a un rectángulo planar infinitamente pequeño.

Proyecciones cilíndricas normales de la esfera han x=aλ λ {displaystyle x=alambda} y Sí.{displaystyle y} igual a una función de latitud solamente. Por lo tanto, el elemento infinitesimal PMQK en la esfera proyecta a un elemento infinitesimal P'M'Q'K' que es un exacta rectángulo con una base δ δ x=aδ δ λ λ {displaystyle delta x=a,delta lambda } y altura δ δ Sí.{displaystyle delta y}. Al comparar los elementos en la esfera y proyección podemos deducir inmediatamente expresiones para los factores de escala en paralelos y meridianos. (El tratamiento de la escala en una dirección general puede encontrarse a continuación.)
- factor de escala paralela k=δ δ xa# φ φ δ δ λ λ =sec φ φ {displaystyle quad k;=;{dfrac {delta x}{acos varphi ,delta lambda ,}=, varphi qquad qquad {}
- factor de escala meridiana h=δ δ Sí.aδ δ φ φ =Sí..()φ φ )a{displaystyle quad h;=;{dfrac {delta y}{a,delta varphi ¿Qué?
Note que el factor de escala paralela k=sec φ φ {displaystyle k=sec varphi } es independiente de la definición de Sí.()φ φ ){displaystyle y(varphi)} así que es lo mismo para todas las proyecciones cilíndricas normales. Es útil señalar que
- en latitud 30 grados la escala paralela es k=sec 30∘ ∘ =2/3=1.15{displaystyle k=sec 30^{circu} #2/{sqrt {3}=1.15}
- en latitud 45 grados la escala paralela es k=sec 45∘ ∘ =2=1.414{displaystyle k=sec 45^{circu} }={sqrt {2}=1.414}
- en latitud 60 grados la escala paralela es k=sec 60∘ ∘ =2{displaystyle k=sec 60^{circu} }=2}
- en latitud 80 grados la escala paralela es k=sec 80∘ ∘ =5.76{displaystyle k=sec 80^{circ }=5.76}
- en latitud 85 grados la escala paralela es k=sec 85∘ ∘ =11.5{displaystyle k=sec 85^{circ }=11.5}
Los siguientes ejemplos ilustran tres proyecciones cilíndricas normales y, en cada caso, la variación de la escala con la posición y la dirección se ilustra mediante el uso de la indicatriz de Tissot.
Tres ejemplos de proyección cilíndrica normal
La proyección equirectangular

La proyección equirectangular, también conocida como Plate Carrée (French for "flat square") o (algo engañoso) la proyección equidistante, se define por
- x=aλ λ ,{displaystyle x=alambda} Sí.=aφ φ ,{displaystyle y=avarphi}
Donde a{displaystyle a} es el radio de la esfera, λ λ {displaystyle lambda } es la longitud del meridiano central de la proyección (aquí se toma como el meridiano Greenwich en λ λ =0{displaystyle lambda =0}) y φ φ {displaystyle varphi } es la latitud. Note que λ λ {displaystyle lambda } y φ φ {displaystyle varphi } están en radianos (obtenidos multiplicando la medida de grado por un factor de π π {displaystyle pi}/180). La longitud λ λ {displaystyle lambda } está en el rango [− − π π ,π π ]{displaystyle [-pipi} y la latitud φ φ {displaystyle varphi } está en el rango [− − π π /2,π π /2]{displaystyle [-pi /2,pi /2].
Desde Sí..()φ φ )=1{displaystyle y'(varphi)=1} la sección anterior da
- escala paralela, k=δ δ xa# φ φ δ δ λ λ =sec φ φ {displaystyle quad k;=;{dfrac {delta x}{acos varphi ,delta lambda ,}=, varphi qquad qquad {}
- escala meridiana h=δ δ Sí.aδ δ φ φ =1{displaystyle quad h;=;{dfrac {delta y}{a,delta varphi #
Para el cálculo de la escala de puntos en una dirección arbitraria, consulte el anexo.
La figura ilustra la indicación Tissot para esta proyección. En el ecuador h=k=1 y los elementos circulares son indistorsionados en la proyección. En latitudes superiores los círculos se distorsionan en una elipse dada estirando sólo en la dirección paralela: no hay distorsión en la dirección meridiana. La relación del eje principal con el eje menor es sec φ φ {displaystyle sec varphi }. Claramente el área de la elipse aumenta por el mismo factor.
Es instructivo considerar el uso de escalas de barras que pueden aparecer en una versión impresa de esta proyección. La escala es verdadera (k=1) en el ecuador para que multiplicar su longitud en un mapa impreso por el inverso de la RF (o escala principal) da la circunferencia real de la Tierra. La escala de barras en el mapa también se dibuja en la verdadera escala para que la transferencia de una separación entre dos puntos en el Ecuador a la escala de barras dé la distancia correcta entre esos puntos. Lo mismo ocurre con los meridianos. En un paralelo aparte del Ecuador la escala es sec φ φ {displaystyle sec varphi } así que cuando transferimos una separación de un paralelo a la escala de barras debemos dividir la distancia de la escala de barras por este factor para obtener la distancia entre los puntos cuando se mide a lo largo del paralelo (que no es la verdadera distancia a lo largo de un gran círculo). En una línea en un rodamiento de decir 45 grados (β β =45∘ ∘ {displaystyle beta =45^{circ }) la escala varía continuamente con latitud y transferir una separación a lo largo de la línea a la escala de la barra no da una distancia relacionada con la verdadera distancia de cualquier manera simple. (Pero vea la adición). Incluso si una distancia a lo largo de esta línea de ángulo planificado constante podría ser elaborada, su relevancia es cuestionable ya que tal línea en la proyección corresponde a una curva complicada en la esfera. Por estas razones, las escalas de barras en mapas a pequeña escala deben usarse con extrema precaución.
Proyección de Mercator

El Mercator proyecta la esfera en un rectángulo (de infinita extensión en el Sí.{displaystyle y}-dirección) por las ecuaciones
- x=aλ λ {displaystyle x=alambda ,}
- Sí.=aIn [# ()π π 4+φ φ 2)]{displaystyle y=aln left[tan left({frac {pi {4}}+{frac {varphi}{2}right)right]
donde a, λ λ {displaystyle lambda ,} y φ φ {displaystyle varphi ,} son como en el ejemplo anterior. Desde Sí..()φ φ )=asec φ φ {displaystyle y'(varphi)=asec varphi } los factores de escala son:
- escala paralela k=δ δ xa# φ φ δ δ λ λ =sec φ φ .{displaystyle k;=;{dfrac {delta x}{acos varphi ,delta lambda {fnMicrosoft Sans Serif}
- escala meridiana h=δ δ Sí.aδ δ φ φ =sec φ φ .{displaystyle h;=;{dfrac {delta y}{a,delta varphi {fnMicrosoft Sans Serif}
En la adición matemática se muestra que la escala de puntos en una dirección arbitraria también es igual a sec φ φ {displaystyle sec varphi } por lo que la escala es isotrópica (la misma en todas las direcciones), su magnitud aumenta con la latitud como sec φ φ {displaystyle sec varphi }. En el diagrama Tissot cada elemento circular infinitesimal conserva su forma pero se agranda cada vez más a medida que aumenta la latitud.
Proyección de área igual a Lambert

La proyección de áreas iguales de Lambert asigna la esfera a un rectángulo finito mediante las ecuaciones
- x=aλ λ Sí.=apecado φ φ {displaystyle x=alambda qquad qquad y=asin varphi }
donde a, λ λ {displaystyle lambda } y φ φ {displaystyle varphi } son como en el ejemplo anterior. Desde Sí..()φ φ )=# φ φ {displaystyle y'(varphi)=cos varphi } los factores de escala
- escala paralela k=δ δ xa# φ φ δ δ λ λ =sec φ φ {displaystyle quad k;=;{dfrac {delta x}{acos varphi ,delta lambda ,}=, varphi qquad qquad {}
- escala meridiana h=δ δ Sí.aδ δ φ φ =# φ φ {displaystyle quad h;=;{dfrac {delta y}{a,delta varphi {fnMicrosoft Sans Serif}
A continuación se proporciona el cálculo de la escala de puntos en una dirección arbitraria.
Las escalas vertical y horizontal ahora se compensan entre sí (hk=1) y en el diagrama de Tissot cada elemento circular infinitesimal se distorsiona en una elipse de la misma área que los círculos no distorsionados en el ecuador.
Gráficos de factores de escala

El gráfico muestra la variación de los factores de escala para los tres ejemplos anteriores. El gráfico superior muestra la función de escala isotrópica de Mercator: la escala en el paralelo es la misma que la escala en el meridiano. Los otros gráficos muestran el factor de escala de meridianos para la proyección equirectangular (h=1) y para la proyección de áreas iguales de Lambert. Estas dos últimas proyecciones tienen una escala paralela idéntica a la del gráfico de Mercator. Para Lambert se observa que la escala paralela (como Mercator A) aumenta con la latitud y la escala del meridiano (C) disminuye con la latitud de tal manera que hk=1, garantizando la conservación del área.
Variación de escala en la proyección de Mercator
La escala de puntos Mercator es unidad en el Ecuador porque es tal que el cilindro auxiliar utilizado en su construcción es tangencial a la Tierra en el Ecuador. Por esta razón la proyección habitual debe ser llamada tangente proyección. La escala varía con latitud como k=sec φ φ {displaystyle k=sec varphi }. Desde sec φ φ {displaystyle sec varphi } tiende a la infinidad a medida que nos acercamos a los polos el mapa del Mercator se distorsiona burdamente en altas latitudes y por esta razón la proyección es totalmente inapropiada para los mapas mundiales (a menos que estamos discutiendo navegación y líneas rhumb). Sin embargo, en una latitud de unos 25 grados el valor de sec φ φ {displaystyle sec varphi } es sobre 1.1 así que Mercator es exacto a un 10% en una tira de ancho 50 grados centrado en el Ecuador. Las tiras más estrechas son mejores: una tira de ancho 16 grados (centrada en el Ecuador) es exacta a dentro de 1% o 1 parte en 100.
Un criterio estándar para buenos mapas a gran escala es que la precisión debe estar dentro de 4 partes en 10.000, o 0,04%, correspondiente a k=1.0004{displaystyle k=1.0004}. Desde sec φ φ {displaystyle sec varphi } alcanza este valor a φ φ =1.62{displaystyle varphi =1.62} grados (ver figura abajo, línea roja). Por lo tanto, la proyección tangente Mercator es altamente precisa dentro de una tira de ancho 3.24 grados centrado en el Ecuador. Esto corresponde a la distancia norte-sur de unos 360 km (220 mi). Dentro de esta tira Mercator está muy bien. buena, muy precisa y la preservación de la forma porque es conformal (conservación del triángulo). Estas observaciones impulsaron el desarrollo de las proyecciones transversales del Mercator en las que se trata a un meridiano "como un Ecuador" de la proyección para obtener un mapa preciso a una distancia estrecha de ese meridiano. Estos mapas son buenos para los países alineados casi norte-sur (como Gran Bretaña) y un conjunto de 60 mapas de este tipo se utiliza para el Mercador Transverso Universal (UTM). Tenga en cuenta que en ambas proyecciones (que se basan en varios ellipsoides) las ecuaciones de transformación para x y y y y y la expresión para el factor de escala son funciones complicadas tanto de latitud como de longitud.

Proyecciones secantes o modificadas

La idea básica de una proyección de secant es que la esfera se proyecta a un cilindro que intersecte la esfera en dos paralelos, digamos φ φ 1{displaystyle varphi _{1} norte y sur. Claramente la escala es ahora verdadera en estas latitudes, mientras que los paralelos debajo de estas latitudes se contraen por la proyección y su factor de escala (paralela) debe ser inferior a uno. El resultado es que la desviación de la escala de la unidad se reduce sobre una amplia gama de latitudes.

Como ejemplo, una posible proyección secante de Mercator está definida por
- x=0.9996aλ λ Sí.=0.9996aIn ()# ()π π 4+φ φ 2)).{displaystyle x=0.9996alambda qquad qquad y=0.9996aln left(tan left({frac {pi ¿Qué? }
Los multiplicadores numéricos no alteran la forma de la proyección pero sí que modifican los factores de escala:
- secant escala Mercator, k=0.9996sec φ φ .{displaystyle quad k;=0.9996sec varphi.}
Así
- la escala en el Ecuador es 0.9996,
- la escala k = 1 a una latitud dada por φ φ 1{displaystyle varphi _{1} Donde sec φ φ 1=1/0.9996=1.00004{displaystyle sec varphi _{1}=1/0.9996=1.00004} así φ φ 1=1.62{displaystyle varphi ### {1}=1.62} grados,
- k=1.0004 a una latitud φ φ 2{displaystyle varphi _{2} dado por sec φ φ 2=1.0004/0.9996=1.0008{displaystyle sec varphi _{2}=1.0004/0.9996=1.0008} para el cual φ φ 2=2.29{displaystyle varphi ¿Qué? grados. Por lo tanto, la proyección tiene <math alttext="{displaystyle 1<k1c)kc)1.0004{displaystyle 1 = 0,0004}<img alt="{displaystyle 1<k, que es una precisión de 0,04%, sobre una tira más ancha de 4,58 grados (en comparación con 3,24 grados para la forma tangente).
Esto se ilustra con la curva inferior (verde) en la figura de la sección anterior.
Tales zonas estrechas de alta precisión se utilizan en la proyección UTM y la OSGB británica, ambas secant, Mercator transversal en el ellipsoide con la escala en la constante meridiana central en el k0=0.9996{displaystyle K_{0}=0.9996}. Las líneas isoscales con k=1{displaystyle k=1} son líneas ligeramente curvadas aproximadamente 180 km al este y al oeste del meridiano central. El valor máximo del factor de escala es 1.001 para UTM y 1.0007 para OSGB.
Las líneas de escala unitaria a latitud φ φ 1{displaystyle varphi _{1} (norte y sur), donde la superficie de proyección cilíndrica interseca la esfera, son la paralelos estándar de la proyección de secant.
Golpear una banda estrecha con <math alttext="{displaystyle |k-1|Silenciok− − 1Silencioc)0,0004{displaystyle TENK-1<img alt="{displaystyle |k-1| es importante para el mapeo de alta precisión a gran escala, para los mapas mundiales se utilizan para controlar la variación de la escala mucho más amplios paralelos estándar. Ejemplos son
- Behrmann con paralelos estándar a 30N, 30S.
- Área igual de Gall con paralelos estándar a 45N, 45S.

Los gráficos de escala para este último se muestran a continuación en comparación con los factores de escala de áreas iguales de Lambert. En este último, el ecuador es un paralelo estándar único y la escala del paralelo aumenta desde k=1 para compensar la disminución en la escala del meridiano. Para Gall, la escala paralela se reduce en el ecuador (a k=0,707) mientras que la escala del meridiano aumenta (a k=1,414). Esto da lugar a una gran distorsión de la forma en la proyección de Gall-Peters. (En el mundo, África es tan larga como ancha). Tenga en cuenta que las escalas de meridianos y paralelos son la unidad en los paralelos estándar.
Apéndice matemático

Para proyecciones cilíndricas normales, la geometría de los elementos infinitesimales da
- a)# α α =a# φ φ δ δ λ λ aδ δ φ φ ,{displaystyle {text{(a)}}quad tan alpha ={frac {acos varphi ,delta lambda }{a,delta varphi }}}}
- b)# β β =δ δ xδ δ Sí.=aδ δ λ λ δ δ Sí..{displaystyle {text{(b)}}quad tan beta ={frac {delta x}{delta Y'}={frac {a,delta lambda } {delta y}}
La relación entre los ángulos β β {displaystyle beta } y α α {displaystyle alpha } es
- c)# β β =asec φ φ Sí..()φ φ )# α α .{displaystyle {text{(c)}quad tan beta ={frac {asec varphi }{y'(varphi)}tan alpha.,}
Para la proyección Mercator Sí..()φ φ )=asec φ φ {displaystyle y'(varphi)=asec varphi } dar α α =β β {displaystyle alpha =beta }: los ángulos se conservan. (Hardly sorprendente ya que esta es la relación utilizada para derivar Mercator). Para las proyecciones equidistas y lambert tenemos Sí..()φ φ )=a{displaystyle y'(varphi)=a} y Sí..()φ φ )=a# φ φ {displaystyle y'(varphi)=acos varphi } respectivamente, así como la relación entre α α {displaystyle alpha } y β β {displaystyle beta } depende de la latitud φ φ {displaystyle varphi }. Denota la escala de puntos en P cuando el elemento infinitesimal PQ hace un ángulo α α {displaystyle alpha ,} con el meridiano μ μ α α .{displaystyle mu _{alpha } Se da por la proporción de distancias:
- μ μ α α =limQ→ → PP.Q.PQ=limQ→ → Pδ δ x2+δ δ Sí.2a2δ δ φ φ 2+a2#2 φ φ δ δ λ λ 2.{displaystyle mu _{alpha }=lim _{ Qto P}{frac {P'Q'}=lim _{Qto P}{frac {sqrt {delta x^{2}+delta ¿Qué? ^{2}+a^{2}cos ^{2}varphi ,delta lambda ^{2}}}}}
Ajuste δ δ x=aδ δ λ λ {displaystyle delta x=a,delta lambda } y sustitución δ δ φ φ {displaystyle delta varphi } y δ δ Sí.{displaystyle delta y} de las ecuaciones a) y b) respectivamente
- μ μ α α ()φ φ )=sec φ φ [pecado α α pecado β β ].{displaystyle mu _{alpha }(varphi)=sec varphi left[{frac {sin alpha }{sin beta }right].}
Para las proyecciones que no sean Mercator primero debemos calcular β β {displaystyle beta } desde α α {displaystyle alpha } y φ φ {displaystyle varphi } usando la ecuación (c), antes de que podamos encontrar μ μ α α {displaystyle mu _{alpha }. Por ejemplo, la proyección equirectangular tiene Sí..=a{displaystyle y'=a} así
- # β β =sec φ φ # α α .{displaystyle tan beta = varphi tan alpha.
Si consideramos una línea de pendiente constante β β {displaystyle beta } en la proyección tanto el valor correspondiente α α {displaystyle alpha } y el factor de escala a lo largo de la línea son funciones complicadas φ φ {displaystyle varphi }. No hay manera sencilla de transferir una separación finita general a una escala de barras y obtener resultados significativos.
Símbolo de ratio
Si bien los dos puntos se utilizan a menudo para expresar proporciones, Unicode puede expresar un símbolo específico de proporciones, ligeramente elevado: U+2236 ∶ RELACIÓN (∶).
Contenido relacionado
Longitud geográfica
Área metropolitana
Círculo polar antártico






































![{displaystyle [-pipi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
![{displaystyle [-pi /2,pi /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd702a5a7041be010f870c0e23750d98ba9919f5)





![{displaystyle y=aln left[tan left({frac {pi }{4}}+{frac {varphi }{2}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fd7eea496725653f6c780bcf3c49947d2b48064)






























![{displaystyle mu _{alpha }(varphi)=sec varphi left[{frac {sin alpha }{sin beta }}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55cb43751c9ca5425b86d60bba0f3464394bd09f)


