Epimorfismo

En la teoría de categorías, un epimorfismo (también llamado morfismo épico o, coloquialmente, epi) es un morfismo f : X → Y que se cancela por la derecha en el sentido de que, para todos los objetos Z y todos los morfismos g₁, g₂: Y → Z,

g1∘ ∘ f=g2∘ ∘ f⟹ ⟹ g1=g2.{displaystyle g_{1}circ f=g_{2}circ fimplies g_{1}=g_{2}

Los epimorfismos son análogos categóricos de funciones sobre o subjetivas (y en la categoría de conjuntos el concepto corresponde exactamente a las funciones subjetivas), pero pueden no coincidir exactamente en todos los contextos; por ejemplo, la inclusión Z→ → Q{displaystyle mathbb {Z} to mathbb {Q} es un epimorfismo de anillo. El doble epimorfismo es un monomorfismo (es decir, un epimorfismo en una categoría C es un monomorfismo en la categoría dual C^operaciones).

Muchos autores de álgebra abstracta y álgebra universal definen un epimorfismo simplemente como un homomorfismo sobre o sobreyectivo. Todo epimorfismo en este sentido algebraico es un epimorfismo en el sentido de la teoría de categorías, pero lo contrario no es cierto en todas las categorías. En este artículo, el término "epimorfismo" se utilizará en el sentido de la teoría de categorías dada anteriormente. Para obtener más información sobre esto, consulte § Terminología a continuación.

Ejemplos

Todo morfismo en una categoría concreta cuya función subyacente es sobreyectiva es un epimorfismo. En muchas categorías concretas de interés lo contrario también es cierto. Por ejemplo, en las siguientes categorías, los epimorfismos son exactamente aquellos morfismos que son sobreyectivos en los conjuntos subyacentes:

• Set: conjuntos y funciones. Para demostrar que todo epimorfismo f: X → Y dentro Set es subjetivo, lo componemos con la función característica g₁: Y → {0,1} de la imagen f()X) y el mapa g₂: Y → {0,1} que es constante 1.
• Rel: establece relaciones binarias y funciones de conservación de relaciones. Aquí podemos usar la misma prueba que para Set, equipar {0,1} con la relación completa {0,1}×{0,1}.
• Pos: conjuntos parcialmente ordenados y funciones monotonas. Si f#X, ≤) → (Y, ≤) no es subjetivo, elegir Sí.₀ dentro Y f()X) y dejar g₁: Y → {0,1} ser la función característica de {Sí. Silencio Sí.₀ ≤ Sí.} y g₂: Y → {0,1} la función característica de {Sí. Silencio Sí.₀. Sí.}. Estos mapas son monotono si {0,1} se da el orden estándar 0 iere 1.
• Grp: grupos y homomorfismos de grupo. El resultado de cada epimorfismo en Grp es subjetivo se debe a Otto Schreier (realmente demostró más, mostrando que cada subgrupo es un ecualizador usando el producto libre con un subgrupo amalgamado); una prueba elemental se puede encontrar en (Linderholm 1970).
• FinGrp: grupos finitos y homomorfismos de grupo. También debido a Schreier; la prueba dada en (Linderholm 1970) establece este caso también.
• Ab: grupos abelianos y homomorfismos de grupo.
• K-Vect: espacios vectoriales sobre un campo K y transformaciones K-linear.
• Mod-R: módulos derecho sobre un anillo R y modulo homomorfismos. Esto generaliza los dos ejemplos anteriores; para probar que cada epimorfismo f: X → Y dentro Mod-R es subjetivo, lo componemos con el mapa de cociente canónico g ₁: Y → Y/f()X) y el mapa cero g₂: Y → Y/f()X).
• Top: espacios topológicos y funciones continuas. Para demostrar que cada epimorfismo en Top es subjetivo, procedemos exactamente como Set, dando {0,1} la topología indiscreta, que asegura que todos los mapas considerados son continuos.
• HComp: espacios compactos Hausdorff y funciones continuas. Si f: X → Y no es subjetivo, deja Sí.▪Y−fX. Desde fX está cerrado, por Lemma de Urysohn hay una función continua g₁:Y → [0,1] tal que g₁ es 0 en fX y 1 en Sí.. Nos componemos f con ambos g₁ y la función cero g₂: Y → [0,1].

Sin embargo, también hay muchas categorías concretas de interés donde los epimorfismos no logran ser sobreyectivos. Algunos ejemplos son:

• En la categoría de monoides, Mon, el mapa de inclusión N → Z es un epimorfismo no-surjetivo. Para ver esto, supongamos que g₁ y g₂ son dos mapas distintos de Z a un monoide M. Entonces un poco. n dentro Z, g₁()n) g₂()n), así que g₁()-n) g₂() -n). Cualquiera n o −n está dentro N, así que las restricciones g₁ y g₂ a N son desiguales.
• En la categoría de álgebras sobre anillo conmutativo R, tomar R[N] → R[Z], donde R[G] es el anillo de grupo del grupo G y el morfismo es inducido por la inclusión N → Z como en el ejemplo anterior. Esto se deriva de la observación de que 1 genera el álgebra R[Z] (nota que la unidad en R[Z] es dado por 0 de Z), y el inverso del elemento representado por n dentro Z es sólo el elemento representado por −n. Así cualquier homomorfismo de R[Z] está determinado por su valor en el elemento representado por 1 de Z.
• En la categoría de anillos, Anillo, el mapa de inclusión Z → Q es un epimorfismo no-surjetivo; para ver esto, note que cualquier homomorfismo del anillo en Q está determinada por su acción sobre Z, similar al ejemplo anterior. Un argumento similar muestra que el homomorfismo de anillo natural de cualquier anillo conmutativo R a cualquiera de sus localizaciones es un epimorfismo.
• En la categoría de anillos comunicativos, un homomorfismo generado finitamente de anillos f: R → S es un epimorfismo si y sólo si para todos los ideales primos P de R, el ideal Q generados por f()P) es o S o es primo, y si Q no S, el mapa inducido Frac(R/P) → Frac(S/Q) es un isomorfismo (EGA IV 17.2.6).
• En la categoría de espacios Hausdorff, Haus, los epimorfismos son precisamente las funciones continuas con imágenes densas. Por ejemplo, el mapa de inclusión Q → R, es un epimorfismo no-surjetivo.

Lo anterior difiere del caso de los monomorfismos donde es más frecuente que los monomorfismos sean precisamente aquellos cuyas funciones subyacentes son inyectivas.

En cuanto a ejemplos de epimorfismos en categorías no concretas:

• Si un monoide o anillo se considera como una categoría con un solo objeto (composición de morfismos dados por multiplicación), entonces los epimorfismos son precisamente los elementos correctos.
• Si un gráfico dirigido es considerado como una categoría (objetos son los vértices, los morfismos son los caminos, la composición de los morfismos es la concatenación de caminos), entonces cada uno El morfismo es un epimorfismo.

Propiedades

Todo isomorfismo es un epimorfismo; de hecho, solo se necesita un inverso del lado derecho: si existe un morfismo j: Y → X tal que fj = id_Y, entonces f: X → Y es fácil de ver ser un epimorfismo. Un mapa con una inversa del lado derecho de este tipo se llama split epi. En un topos, un mapa que es a la vez un morfismo mónico y un epimorfismo es un isomorfismo.

La composición de dos epimorfismos es de nuevo un epimorfismo. Si la composición fg de dos morfismos es un epimorfismo, entonces f debe ser un epimorfismo.

Como muestran algunos de los ejemplos anteriores, la propiedad de ser un epimorfismo no está determinada solo por el morfismo, sino también por la categoría de contexto. Si D es una subcategoría de C, entonces cada morfismo en D que es un epimorfismo cuando se considera como un morfismo en C es también un epimorfismo en D. Sin embargo, no es necesario que se cumpla lo contrario; la categoría más pequeña puede (ya menudo lo hará) tener más epimorfismos.

Como para la mayoría de los conceptos en la teoría de categorías, los epimorfismos se conservan bajo equivalencias de categorías: dada una equivalencia F: C → D, a el morfismo f es un epimorfismo en la categoría C si y solo si F(f) es un epimorfismo en D. Una dualidad entre dos categorías convierte los epimorfismos en monomorfismos y viceversa.

La definición de epimorfismo se puede reformular para establecer que f: X → Y es un epimorfismo si y solo si los mapas inducidos

Hom⁡ ⁡ ()Y,Z)→ → Hom⁡ ⁡ ()X,Z)g↦ ↦ gf{displaystyle {begin{matrix}operatorname {Hom} (Y,Z) {Hom}gnuncio}gnunciognuncio}}

son inyectivos para cada elección de Z. Esto a su vez es equivalente a la transformación natural inducida

Hom⁡ ⁡ ()Y,− − )→ → Hom⁡ ⁡ ()X,− − ){displaystyle {begin{matrix}operatorname {Hom} (Y,-) {Hom}end{matrix}}}

siendo un monomorfismo en la categoría de funtores Set^C.

Todo coecualizador es un epimorfismo, consecuencia del requisito de unicidad en la definición de coecualizadores. Se sigue en particular que todo conúcleo es un epimorfismo. Lo contrario, es decir, que todo epimorfismo sea un coigualador, no es cierto en todas las categorías.

En muchas categorías es posible escribir cada morfismo como la composición de un epimorfismo seguido de un monomorfismo. Por ejemplo, dado un homomorfismo de grupo f: G → H, podemos definir el grupo K = im(f) y luego escribir f como la composición del homomorfismo sobreyectivo G → K que se define como f, seguido del homomorfismo inyectivo K → H que envía cada elemento a sí mismo. Tal factorización de un morfismo arbitrario en un epimorfismo seguido de un monomorfismo puede llevarse a cabo en todas las categorías abelianas y también en todas las categorías concretas mencionadas anteriormente en § Ejemplos (aunque no en todas las categorías concretas).

Conceptos relacionados

Entre otros conceptos útiles se encuentran epimorfismo regular, epimorfismo extremo, epimorfismo inmediato, epimorfismo fuerte y epimorfismo dividido.

• Se dice que un epimorfismo es ordinario si es un coequalizer de un par de morfismos paralelos.
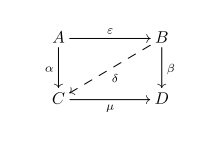
• Un epimorfismo ε ε {displaystyle varepsilon } se dice que extremal si en cada representación ε ε =μ μ ∘ ∘ φ φ {displaystyle varepsilon =mu circ varphi }, donde μ μ {displaystyle mu } es un monomorfismo, el morfismo μ μ {displaystyle mu } es automáticamente un isomorfismo.
• Un epimorfismo ε ε {displaystyle varepsilon } se dice que inmediata si en cada representación ε ε =μ μ ∘ ∘ ε ε .{displaystyle varepsilon =mu circ varepsilon '}, donde μ μ {displaystyle mu } es un monomorfismo y ε ε .{displaystyle varepsilon} es un epimorfismo, el morfismo μ μ {displaystyle mu } es automáticamente un isomorfismo.
• 
  Un epimorfismo ε ε :A→ → B{displaystyle varepsilon: Ato B} se dice que fuerte si para cualquier monomorfismo μ μ :C→ → D{displaystyle mu:Cto D} y cualquier morfismo α α :A→ → C{displaystyle alpha:Ato C} y β β :B→ → D{displaystyle beta:Bto D} tales que β β ∘ ∘ ε ε =μ μ ∘ ∘ α α {displaystyle beta circ varepsilon =mu circ alpha }, existe un morfismo δ δ :B→ → C{displaystyle delta: Bto C} tales que δ δ ∘ ∘ ε ε =α α {displaystyle delta circ varepsilon =alpha } y μ μ ∘ ∘ δ δ =β β {displaystyle mu circ delta =beta }.
• Un epimorfismo ε ε {displaystyle varepsilon } se dice que división si existe un morfismo μ μ {displaystyle mu } tales que ε ε ∘ ∘ μ μ =1{displaystyle varepsilon circ mu =1} (en este caso μ μ {displaystyle mu } se llama un inverso del lado derecho para ε ε {displaystyle varepsilon }).

También existe la noción de epimorfismo homológico en la teoría de anillos. Un morfismo f: A → B de anillos es un epimorfismo homológico si es un epimorfismo e induce un funtor completo y fiel sobre categorías derivadas: D(f): D(B) → D(A).

Un morfismo que es a la vez monomorfismo y epimorfismo se denomina bimorfismo. Todo isomorfismo es un bimorfismo, pero lo contrario no es cierto en general. Por ejemplo, el mapa del intervalo semiabierto [0,1) al círculo unitario S¹ (pensado como un subespacio del plano complejo) que envía x to exp(2πix) (vea la fórmula de Euler) es continua y biyectiva pero no un homeomorfismo ya que la función inversa no es continua en 1, por lo que es una instancia de un bimorfismo que es no es un isomorfismo en la categoría Superior. Otro ejemplo es la incorporación de Q → R en la categoría Haus; como se señaló anteriormente, es un bimorfismo, pero no es biyectiva y, por lo tanto, no es un isomorfismo. De manera similar, en la categoría de anillos, el mapa Z → Q es un bimorfismo pero no un isomorfismo.

Los epimorfismos se utilizan para definir objetos cocientes abstractos en categorías generales: dos epimorfismos f₁: X → Y₁ y f₂: X → Y₂ se dice que son equivalentes si existe un isomorfismo j: Y₁ → Y₂ con j f₁ = f₂. Esta es una relación de equivalencia, y las clases de equivalencia se definen como los objetos cocientes de X.

Terminología

Los términos complementarios epimorfismo y monomorfismo fueron introducidos por primera vez por Bourbaki. Bourbaki usa epimorfismo como abreviatura de una función sobreyectiva. Los primeros teóricos de categorías creían que los epimorfismos eran el análogo correcto de las sobreyecciones en una categoría arbitraria, de forma similar a cómo los monomorfismos son casi un análogo exacto de las inyecciones. Desafortunadamente esto es incorrecto; los epimorfismos fuertes o regulares se comportan mucho más cerca de las sobreyecciones que los epimorfismos ordinarios. Saunders Mac Lane intentó crear una distinción entre epimorfismos, que eran mapas en una categoría concreta cuyos mapas de conjuntos subyacentes eran sobreyectivos, y morfismos épicos, que son epimorfismos en el sentido moderno.. Sin embargo, esta distinción nunca se popularizó.

Es un error común creer que los epimorfismos son idénticos a las sobreyecciones o que son un concepto mejor. Por desgracia, esto no suele ser el caso; los epimorfismos pueden ser muy misteriosos y tener un comportamiento inesperado. Es muy difícil, por ejemplo, clasificar todos los epimorfismos de anillos. En general, los epimorfismos son su propio concepto único, relacionado con sobreyecciones pero fundamentalmente diferente.