Energía de ionización

Compartir Imprimir Citar
Energía necesaria para eliminar un electrón
Tendencias energéticas de ionización trazadas contra el número atómico, en unidades eV. La energía de ionización aumenta gradualmente de los metales alcalinos a los gases nobles. La energía máxima de ionización también disminuye de la primera a la última fila en una columna dada, debido a la creciente distancia de la cáscara de electrones de valence del núcleo. Los valores predecidos se utilizan para elementos más allá de 104.

En física y química, energía de ionización (IE) (ortografía en inglés americano), energía de ionización (ortografía en inglés británico) es el mínimo energía necesaria para eliminar el electrón más débilmente unido de un átomo gaseoso aislado, ion positivo o molécula. La primera energía de ionización se expresa cuantitativamente como

X(g) + energía  X+g) + e−

donde X es cualquier átomo o molécula, X+ es el ion resultante cuando se despojó al átomo original de un solo electrón, y e− es el electrón eliminado. La energía de ionización es positiva para los átomos neutros, lo que significa que la ionización es un proceso endotérmico. En términos generales, cuanto más cerca están los electrones más externos del núcleo del átomo, mayor es la energía de ionización del átomo.

En física, la energía de ionización generalmente se expresa en electronvoltios (eV) o julios (J). En química, se expresa como la energía para ionizar un mol de átomos o moléculas, generalmente como kilojulios por mol (kJ/mol) o kilocalorías por mol (kcal/mol).

La comparación de las energías de ionización de los átomos en la tabla periódica revela dos tendencias periódicas que siguen las reglas de la atracción de Coulombic:

  1. La energía de la ionización generalmente aumenta de izquierda a derecha dentro de un período determinado (es decir, fila).
  2. La energía de la ionización generalmente disminuye de arriba a abajo en un grupo determinado (es decir, columna).

La última tendencia se debe a que la capa externa de electrones se aleja progresivamente del núcleo, con la adición de una capa interna por fila a medida que uno se desplaza hacia abajo en la columna.

La nésima energía de ionización se refiere a la cantidad de energía necesaria para eliminar el electrón más débilmente unido de las especies que tienen una carga positiva de (n − 1). Por ejemplo, las tres primeras energías de ionización se definen de la siguiente manera:

La primera energía de ionización es la energía que permite la reacción X  X+ + e−
2a energía de ionización es la energía que permite la reacción X+  X2+ + e−
3a energía de ionización es la energía que permite la reacción X2+  X3+ + e−

Las influencias más notables que determinan la energía de ionización incluyen:

Las influencias menores incluyen:

El término potencial de ionización es un término antiguo y obsoleto para la energía de ionización, porque el método más antiguo para medir la energía de ionización se basaba en ionizar una muestra y acelerar el electrón eliminado mediante un potencial electrostático.

Determinación de las energías de ionización

Aparato de medición de energía de ionización.

La energía de ionización de los átomos, denominada Ei, se mide encontrando la energía mínima de los cuantos de luz (fotones) o electrones acelerados a una energía conocida que pateará los electrones atómicos menos ligados. La medición se realiza en fase gaseosa en átomos individuales. Si bien solo los gases nobles se presentan como gases monoatómicos, otros gases se pueden dividir en átomos individuales. Además, muchos elementos sólidos se pueden calentar y vaporizar en átomos individuales. El vapor monoatómico está contenido en un tubo previamente evacuado que tiene dos electrodos paralelos conectados a una fuente de voltaje. La excitación ionizante se introduce a través de las paredes del tubo o se produce en su interior.

Cuando se usa luz ultravioleta, la longitud de onda se desplaza hacia abajo en el rango ultravioleta. A una determinada longitud de onda (λ) y frecuencia de luz (ν=c/λ, donde c es la velocidad de la luz), los cuantos de luz, cuya energía es proporcional a la frecuencia, tendrán una energía lo suficientemente alta como para desalojar los electrones menos unidos.. Estos electrones serán atraídos por el electrodo positivo y los iones positivos que queden después de la fotoionización serán atraídos por el electrodo con carga negativa. Estos electrones e iones establecerán una corriente a través del tubo. La energía de ionización será la energía de los fotones hνi (h es la constante de Planck) que causaron un fuerte aumento en la corriente: Ei = hνi.

Cuando se utilizan electrones de alta velocidad para ionizar los átomos, se producen mediante un cañón de electrones dentro de un tubo de vacío similar. La energía del haz de electrones puede ser controlada por los voltajes de aceleración. La energía de estos electrones que da lugar a un inicio brusco de la corriente de iones y electrones liberados a través del tubo coincidirá con la energía de ionización de los átomos.

Átomos: valores y tendencias

Generalmente, la (N+1)-ésima energía de ionización de un elemento en particular es mayor que la Nésima energía de ionización (también se puede notar que la energía de ionización de un anión es generalmente menor que la de cationes y átomo neutro para el mismo elemento). Cuando la siguiente energía de ionización implica la eliminación de un electrón de la misma capa de electrones, el aumento de la energía de ionización se debe principalmente al aumento de la carga neta del ion del que se elimina el electrón. Los electrones extraídos de iones más cargados experimentan mayores fuerzas de atracción electrostática; por lo tanto, su eliminación requiere más energía. Además, cuando la próxima energía de ionización involucra la eliminación de un electrón de una capa de electrones inferior, la distancia mucho menor entre el núcleo y el electrón también aumenta tanto la fuerza electrostática como la distancia sobre la cual se debe superar esa fuerza para eliminar el electrón. Ambos factores aumentan aún más la energía de ionización.

Algunos valores para los elementos del tercer período se dan en la siguiente tabla:

Valores de energía de ionización exitosa / kJ mol−1
(96.485 kJ mol−1 1 eV)
Elemento Primera Segundo Tercera Cuarto Quinta Sexta Séptimo
Na 496 4,560
Mg 738 1.450 7.730
Al 577 1.816 2.881 11.600
Si 786 1,577 3.228 4.354 16.100
P 1.060 1.890 2,905 4.950 6.270 21.200
S 1.000 2.295 3.375 4,565 6.950 8.490 27.107
Cl 1.256 2.260 3,850 5,160 6.560 9.360 11.
Ar 1,520 2.665 3.945 5.770 7.230 8.780 12.000

Se producen grandes saltos en las energías de ionización molares sucesivas al pasar por configuraciones de gases nobles. Por ejemplo, como se puede ver en la tabla anterior, las energías de ionización de los dos primeros molares del magnesio (quitando los dos electrones 3s de un átomo de magnesio) son mucho más pequeñas que la tercera, que requiere quitar un electrón 2p de la configuración de neón de Mg2+. Ese electrón 2p está mucho más cerca del núcleo que los electrones 3s eliminados anteriormente.

Las energías de ionización alcanzan el pico de los gases nobles al final de cada período en la tabla periódica de elementos y, por regla general, sumergen cuando una nueva cáscara comienza a llenarse.

La energía de ionización también es una tendencia periódica dentro de la tabla periódica. Moviéndose de izquierda a derecha dentro de un período, o hacia arriba dentro de un grupo, la primera energía de ionización generalmente aumenta, con excepciones como el aluminio y el azufre en la tabla anterior. A medida que aumenta la carga nuclear del núcleo a lo largo del período, aumenta la atracción electrostática entre los electrones y los protones, por lo que el radio atómico disminuye y la nube de electrones se acerca al núcleo porque los electrones, especialmente el más externo, están retenidos con más fuerza por la mayor carga nuclear efectiva.

Al moverse hacia abajo dentro de un grupo dado, los electrones se mantienen en capas de mayor energía con un número cuántico principal n más alto, más alejados del núcleo y, por lo tanto, se unen de manera más flexible, por lo que la energía de ionización disminuye. La carga nuclear efectiva aumenta lentamente, de modo que su efecto se ve contrarrestado por el aumento de n.

Excepciones en energías de ionización

Hay excepciones a la tendencia general de aumento de las energías de ionización dentro de un período. Por ejemplo, el valor disminuye de berilio (
4Be
: 9,3 eV) a boro (
5B
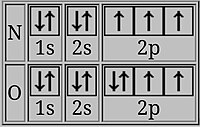
: 8,3 eV), y de nitrógeno (
7N
: 14,5 eV) a oxígeno (
8 O
: 13,6 eV). Estas caídas se pueden explicar en términos de configuraciones electrónicas.

El electron añadido en el borón ocupa un p-orbital.

El boro tiene su último electrón en un orbital 2p, que tiene su densidad electrónica más lejos del núcleo en promedio que los electrones 2s en la misma capa. Los electrones 2s luego protegen al electrón 2p del núcleo hasta cierto punto, y es más fácil eliminar el electrón 2p del boro que eliminar un electrón 2s del berilio, lo que resulta en una energía de ionización más baja para B.

Nitrogen and oxygen's electron configuration
Estas configuraciones de electrones no muestran los orbitales completos y medio llenos.
Nitrogen and oxygen's electron configuration using box and arrows
Aquí el electron añadido tiene un giro opuesto a los otros electrones 2p. Esto disminuye la energía de ionización del oxígeno

En el oxígeno, el último electrón comparte un orbital p doblemente ocupado con un electrón de espín opuesto. Los dos electrones en el mismo orbital están más juntos en promedio que dos electrones en diferentes orbitales, por lo que se protegen entre sí de manera más efectiva y es más fácil eliminar uno, lo que resulta en una energía de ionización más baja.

Además, después de cada elemento de gas noble, la energía de ionización cae drásticamente. Esto ocurre porque el electrón externo en los metales alcalinos requiere una cantidad mucho menor de energía para ser eliminado del átomo que las capas internas. Esto también da lugar a valores de electronegatividad bajos para los metales alcalinos.

Zinc and Gallium's respective electron configurations
Debido a un solo electron p-orbital en la configuración de gallium, hace que la estructura general sea menos estable, por lo tanto el dip en los valores energéticos de ionización
Radium and Actinium's Electron Configuration (condensed)
La configuración de electrones de Actinium predetermina que requeriría menos energía para eliminar ese solo electron d-orbital, por lo tanto, aunque tenga una EC más grande, el radio todavía tiene el mayor IE

Las tendencias y excepciones se resumen en las siguientes subsecciones:

La energía de ionización disminuye cuando

La energía de ionización aumenta cuando

Anomalías de energía de ionización en grupos

Los valores de energía de ionización tienden a disminuir al pasar a elementos más pesados dentro de un grupo, ya que más electrones proporcionan protección y, en general, las capas de valencia experimentan una atracción más débil del núcleo, atribuido al radio covalente más grande que aumenta al descender por un grupo Sin embargo, este no es siempre el caso. Como excepción, en el grupo 10 paladio (
46Pd
: 8,34 eV) tiene una energía de ionización más alta que el níquel (
28Ni
: 7,64 eV), contrario a la disminución general de los elementos de tecnecio
43Tc
 a xenón
54Xe
. Estas anomalías se resumen a continuación:

Modelo de Bohr para átomo de hidrógeno

La energía de ionización del átomo de hidrógeno (Z=1{displaystyle Z=1}) se puede evaluar en el modelo Bohr, que predice que el nivel de energía atómica n{displaystyle n} tiene energía

E=− − 1n2Z2e22a0=− − Z2RHn2=− − Z213.6eVn2{displaystyle E=-{frac {1} {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}} {fn}}}} {fn}}} {fn}} {fn}}} {fn}}} {fn}}}} {fn}}} {f}}}} {f}}} {f}}}}} {f}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {fn}}}}}}}}}} {f}} {f} {f} {f} {fn}}}}}}}}}}}}}}}}} {f}}}}f} {f} {f} {f} {fnfn}}}}}}}}}}}}}}}}}}}}}}}} {Z^{2}e^{2}{2a_{0}=-{frac} {Z^{2}R_{H} {n^{2}}={frac} {Z^{2}13.6 mathrm {eV} {n^{2}}}}}}

RH es la constante Rydberg para el átomo de hidrógeno. Para hidrógeno en el estado del suelo Z=1{displaystyle Z=1} y n=1{displaystyle n=1} para que la energía del átomo antes de la ionización sea simplemente E=− − 13.6eV{displaystyle E=-13.6mathrm {eV}

Después de la ionización, la energía es cero para un electrón inmóvil infinitamente lejos del protón, por lo que la energía de ionización es

I=E()H+)− − E()H)=+13.6eV{displaystyle I=E(mathrm [H} ^{+})-E(mathrm {H})=+13.6\mathrm {eV}. Esto coincide con el valor experimental del átomo de hidrógeno.

Explicación mecánica cuántica

Según la teoría más completa de la mecánica cuántica, la ubicación de un electrón se describe mejor como una distribución de probabilidad dentro de una nube de electrones, es decir, un orbital atómico. La energía se puede calcular integrando sobre esta nube. La representación matemática subyacente de la nube es la función de onda, que se construye a partir de determinantes de Slater que consisten en orbitales de espín molecular. Estos están relacionados por el principio de exclusión de Pauli con los productos antisimetrizados de los orbitales atómicos o moleculares.

Hay dos formas principales de calcular la energía de ionización. En general, el cálculo para el Nla energía de ionización requiere calcular las energías de Z− − N+1{displaystyle Z-N+1} y Z− − N{displaystyle Z-N. Sistemas de electrones. Cálculo de estas energías exactamente no es posible excepto para los sistemas más simples (es decir, elementos de hidrógeno e hidrógeno), principalmente debido a dificultades para integrar los términos de correlación de electrones. Por lo tanto, los métodos de aproximación se emplean rutinariamente, con diferentes métodos que varían en complejidad (tiempo computacional) y precisión en comparación con los datos empíricos. Esto se ha convertido en un problema bien estudiado y se hace rutinariamente en la química computacional. La segunda manera de calcular las energías de ionización se utiliza principalmente en el nivel más bajo de la aproximación, donde la energía de ionización es proporcionada por el teorema de Koopmans, que implica la órbita molecular más alta ocupada o "HOMO" y la órbita molecular más baja no ocupada o "LUMO", y afirma que la energía de ionización de un átomo o molécula es igual a la energía de la órbita de la cual se expulsa el electrón. Esto significa que la energía de ionización es igual a la energía HOMO, que en una ecuación formal se puede escribir como: Ii=− − Ei{displaystyle I_{i}=-E_{i}.

Moléculas: energía de ionización vertical y adiabática

Gráfico 1 Esquema de energía de principio de Franck-Condon. Para la ionización de una molécula diatómica, la única coordinación nuclear es la longitud de unión. La curva inferior es la curva de energía potencial de la molécula neutra, y la curva superior es para el ion positivo con una longitud de unión más larga. La flecha azul es ionización vertical, aquí desde el estado del suelo de la molécula hasta el nivel v=2 del ion.

La ionización de moléculas a menudo conduce a cambios en la geometría molecular, y se definen dos tipos de (primera) energía de ionización: adiabático y vertical.

Energía de ionización adiabática

La energía de ionización adiabática de una molécula es la cantidad mínima de energía necesaria para extraer un electrón de una molécula neutra, es decir, la diferencia entre la energía del estado fundamental vibracional de las especies neutras (v& #34; = 0 nivel) y la del ion positivo (v' = 0). La geometría de equilibrio específica de cada especie no afecta este valor.

Energía de ionización vertical

Debido a los posibles cambios en la geometría molecular que pueden resultar de la ionización, pueden existir transiciones adicionales entre el estado fundamental vibratorio de las especies neutras y los estados vibratorios excitados del ion positivo. En otras palabras, la ionización va acompañada de excitación vibratoria. La intensidad de tales transiciones se explica por el principio de Franck-Condon, que predice que la transición más probable e intensa corresponde al estado vibracionalmente excitado del ion positivo que tiene la misma geometría que la molécula neutra. Esta transición se conoce como "vertical" energía de ionización ya que está representada por una línea completamente vertical en un diagrama de energía potencial (ver Figura).

Para una molécula diatómica, la geometría se define por la longitud de un enlace sencillo. La eliminación de un electrón de un orbital molecular enlazante debilita el enlace y aumenta la longitud del enlace. En la Figura 1, la curva de energía potencial inferior es para la molécula neutra y la superficie superior es para el ion positivo. Ambas curvas trazan la energía potencial en función de la longitud del enlace. Las líneas horizontales corresponden a los niveles de vibración con sus funciones de onda vibratoria asociadas. Dado que el ion tiene un enlace más débil, tendrá una longitud de enlace más larga. Este efecto se representa desplazando el mínimo de la curva de energía potencial hacia la derecha de la especie neutra. La ionización adiabática es la transición diagonal al estado fundamental vibracional del ion. La ionización vertical puede implicar una excitación vibratoria del estado iónico y, por lo tanto, requiere una mayor energía.

En muchas circunstancias, la energía de ionización adiabática suele ser una cantidad física más interesante, ya que describe la diferencia de energía entre las dos superficies de energía potencial. Sin embargo, debido a limitaciones experimentales, la energía de ionización adiabática suele ser difícil de determinar, mientras que la energía de desprendimiento vertical es fácilmente identificable y medible.

Análogos de la energía de ionización a otros sistemas

Si bien el término energía de ionización se usa principalmente solo para especies atómicas, catiónicas o moleculares en fase gaseosa, hay una serie de cantidades análogas que consideran la cantidad de energía necesaria para extraer un electrón de otros sistemas físicos.

Energía de enlace de electrones

Energías vinculantes de órbitas atómicas específicas como función del número atómico. Debido al creciente número de protones, los electrones que ocupan el mismo orbital están más unidos en elementos más pesados.

La energía de enlace de electrones es un término genérico para la energía mínima necesaria para eliminar un electrón de una capa de electrones particular para un átomo o ion, debido a que estos electrones cargados negativamente se mantienen en su lugar por la atracción electrostática del núcleo cargado positivamente. Por ejemplo, la energía de enlace de electrones para quitar un electrón 3p3/2 del ion cloruro es la cantidad mínima de energía requerida para quitar un electrón del átomo de cloro cuando tiene una carga de -1. En este ejemplo particular, la energía de enlace de electrones tiene la misma magnitud que la afinidad electrónica por el átomo de cloro neutro. En otro ejemplo, la energía de enlace de electrones se refiere a la cantidad mínima de energía requerida para eliminar un electrón del dianión de dicarboxilato −O2C(CH2)8CO−
2.

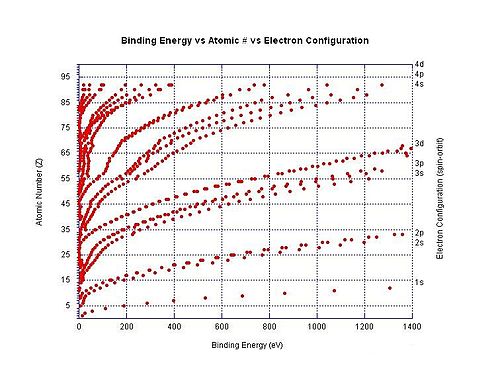
El gráfico de la derecha muestra la energía de enlace de los electrones en diferentes capas en átomos neutros. La energía de ionización es la energía de enlace más baja para un átomo en particular (aunque no se muestran todas en el gráfico).

Superficies sólidas: función de trabajo

La función de trabajo es la cantidad mínima de energía necesaria para extraer un electrón de una superficie sólida, donde la función de trabajo W para una superficie dada es definida por la diferencia

W=− − eφ φ − − EF,{displaystyle ¿Qué?

donde −e es la carga de un electrón, ϕ es el potencial electrostático en el vacío cerca de la superficie, y EF es el nivel de Fermi (potencial electroquímico de electrones) dentro del material.

Nota

  1. ^ No obstante, aún es necesario seguir investigando para corroborar esta mera inferencia.