Efecto isotópico cinético

En química orgánica física, un efecto de isótopo cinético (KIE) es el cambio en la velocidad de reacción de una reacción química cuando uno de los átomos en los reactivos es reemplazado por uno de sus isótopos. Formalmente, es la relación de constantes de velocidad para las reacciones que involucran los reactivos sustituidos isotópicamente ligeros (k _L) y pesados ​​(k _H) (isotopólogos):

Este cambio en la velocidad de reacción es un efecto mecánico cuántico que resulta principalmente de isotopólogos más pesados ​​que tienen frecuencias vibratorias más bajas en comparación con sus contrapartes más ligeras. En la mayoría de los casos, esto implica un mayor aporte energético necesario para que los isotopólogos más pesados ​​alcancen el estado de transición (o, en casos excepcionales, el límite de disociación) y, en consecuencia, una velocidad de reacción más lenta. El estudio de los efectos de los isótopos cinéticos puede ayudar a dilucidar el mecanismo de reacción de ciertas reacciones químicas y ocasionalmente se aprovecha en el desarrollo de fármacos para mejorar la farmacocinética desfavorable al proteger los enlaces CH metabólicamente vulnerables.

Fondo

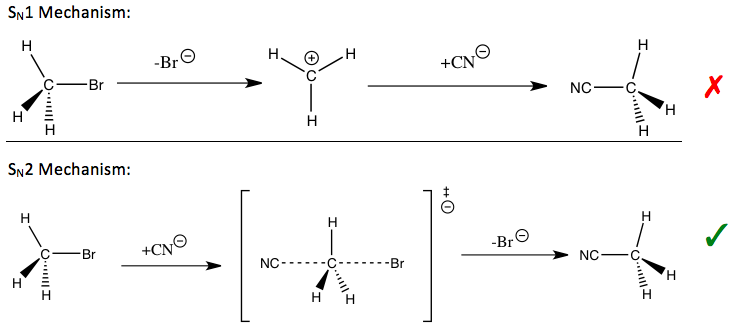
El efecto isotópico cinético se considera una de las herramientas más esenciales y sensibles para el estudio de los mecanismos de reacción, cuyo conocimiento permite mejorar las cualidades deseables de las reacciones correspondientes. Por ejemplo, los efectos isotópicos cinéticos se pueden utilizar para revelar si una reacción de sustitución nucleófila sigue una vía unimolecular (S _N 1) o bimolecular (S _N 2).

En la reacción de bromuro de metilo y cianuro (que se muestra en la introducción), el efecto isotópico cinético de carbono de metilo observado indica un mecanismo S _{N 2.} Dependiendo de la ruta, se pueden usar diferentes estrategias para estabilizar el estado de transición del paso determinante de la velocidad de la reacción y mejorar la velocidad de reacción y la selectividad, que son importantes para las aplicaciones industriales.

Los cambios de velocidad isotópica son más pronunciados cuando el cambio de masa relativa es mayor, ya que el efecto está relacionado con las frecuencias vibratorias de los enlaces afectados. Por ejemplo, cambiar un átomo de hidrógeno (H) por su isótopo deuterio (D) representa un aumento del 100 % en la masa, mientras que al reemplazar el carbono 12 por el carbono 13, la masa aumenta solo un 8 %. La velocidad de una reacción que involucra un enlace C-H es típicamente de 6 a 10 veces más rápida que la del enlace C-D correspondiente, mientras que una reacción C es solo un 4 por ciento más rápida que la reacción C correspondiente (aunque, en ambos casos, el isótopo es una unidad de masa atómica más pesada).

La sustitución isotópica puede modificar la velocidad de reacción de varias formas. En muchos casos, la diferencia de velocidad se puede racionalizar observando que la masa de un átomo afecta la frecuencia vibratoria del enlace químico que forma, incluso si la superficie de energía potencial para la reacción es casi idéntica. Los isótopos más pesados ​​conducirán (clásicamente) a frecuencias de vibración más bajas o, visto desde la mecánica cuántica, tendrán una energía de punto cero más baja. Con una energía de punto cero más baja, se debe suministrar más energía para romper el enlace, lo que da como resultado una energía de activación más alta para la escisión del enlace, lo que a su vez reduce la tasa medida (ver, por ejemplo, la ecuación de Arrhenius).

Clasificación

Efectos isotópicos cinéticos primarios

Se puede encontrar un efecto de isótopo cinético primario cuando se forma o se rompe un enlace con el átomo marcado isotópicamente. Dependiendo de la forma en que se prueba el efecto de un isótopo cinético (medición paralela de velocidades frente a competencia intermolecular frente a competencia intramolecular), la observación de un efecto de isótopo cinético primario es indicativa de la ruptura/formación de un enlace con el isótopo en el paso de limitación de la velocidad., o paso(s) posterior(es) determinante(s) del producto. (La idea errónea de que un efecto de isótopo cinético primario debe reflejar la ruptura/formación de enlaces con el isótopo en el paso limitante de la velocidad se repite con frecuencia en los libros de texto y en la literatura primaria: consulte la sección sobre experimentos a continuación).

Para las reacciones de sustitución nucleófila mencionadas anteriormente, se han investigado los efectos isotópicos cinéticos primarios para los grupos salientes, los nucleófilos y el carbono α en el que se produce la sustitución. La interpretación de los efectos de los isótopos cinéticos del grupo saliente había sido difícil al principio debido a las importantes contribuciones de los factores independientes de la temperatura. Los efectos de isótopos cinéticos en el carbono α se pueden utilizar para desarrollar cierta comprensión de la simetría del estado de transición en las reacciones S _N 2, aunque este efecto de isótopos cinéticos es menos sensible de lo que sería ideal, también debido a la contribución de no vibracional factores

Efectos isotópicos cinéticos secundarios

Se observa un efecto isotópico cinético secundario cuando no se rompe ni se forma ningún enlace con el átomo marcado isotópicamente en el reactivo. Los efectos isotópicos cinéticos secundarios tienden a ser mucho más pequeños que los efectos isotópicos cinéticos primarios; sin embargo, los efectos secundarios de los isótopos de deuterio pueden ser tan grandes como 1,4 por átomo de deuterio, y se han desarrollado técnicas para medir los efectos de los isótopos de elementos pesados ​​con una precisión muy alta, por lo que los efectos secundarios de los isótopos cinéticos siguen siendo muy útiles para dilucidar los mecanismos de reacción.

Para las reacciones de sustitución nucleófila antes mencionadas, los efectos isotópicos cinéticos del hidrógeno secundario en el carbono α proporcionan un medio directo para distinguir entre las reacciones S _N 1 y S _N 2. Se ha encontrado que las reacciones S _N 1 típicamente conducen a grandes efectos isotópicos cinéticos secundarios, acercándose a su máximo teórico en aproximadamente 1.22, mientras que las reacciones S _N 2 típicamente producen efectos isotópicos cinéticos primarios que están muy cerca o menos que la unidad. Los efectos isotópicos cinéticos mayores que 1 se denominan efectos isotópicos cinéticos normales, mientras que los efectos isotópicos cinéticos menores que uno se denominan efectos isotópicos cinéticos inversos.. En general, se espera que las constantes de fuerza más pequeñas en el estado de transición produzcan un efecto de isótopo cinético normal, y las constantes de fuerza más grandes en el estado de transición se espera que produzcan un efecto de isótopo cinético inverso cuando las contribuciones vibratorias de estiramiento dominan el efecto de isótopo cinético.

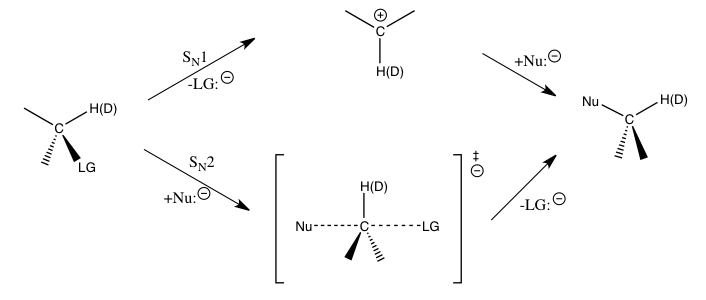
Las magnitudes de tales efectos isotópicos secundarios en el átomo de carbono α están determinadas en gran medida por las vibraciones C _α -H(D). Para una reacción S _N 1, dado que el átomo de carbono se convierte en un ion carbenio con hibridación sp durante el estado de transición para el paso determinante de la velocidad con un aumento en el orden de enlace C _α -H(D), un efecto isotópico cinético inverso sería esperado si sólo las vibraciones de estiramiento fueran importantes. Se encuentra que los grandes efectos isotópicos cinéticos normales observados son causados ​​por importantes contribuciones vibratorias de flexión fuera del plano cuando se pasa de los reactivos al estado de transición de formación de iones carbenio. Para _SN2, las vibraciones de flexión aún juegan un papel importante para el efecto isotópico cinético, pero las contribuciones vibratorias de estiramiento son de una magnitud más comparable, y el efecto isotópico cinético resultante puede ser normal o inverso dependiendo de las contribuciones específicas de las vibraciones respectivas.

Teoría

El tratamiento teórico de los efectos isotópicos se basa en gran medida en la teoría del estado de transición, que asume una única superficie de energía potencial para la reacción y una barrera entre los reactivos y los productos en esta superficie, encima de la cual reside el estado de transición.El efecto del isótopo cinético surge en gran medida de los cambios en los estados fundamentales de vibración producidos por la perturbación isotópica a lo largo de la ruta de energía mínima de la superficie de energía potencial, que solo puede explicarse con tratamientos mecánicos cuánticos del sistema. Según la masa del átomo que se mueve a lo largo de la coordenada de reacción y la naturaleza (ancho y alto) de la barrera de energía, la tunelización de la mecánica cuántica también puede contribuir en gran medida a un efecto isotópico cinético observado y es posible que deba considerarse por separado, además al modelo de teoría del estado de transición "semiclásico".

El efecto del isótopo cinético del deuterio (H KIE) es, con mucho, el tipo de efecto isotópico cinético más común, útil y mejor entendido. La predicción precisa del valor numérico del efecto de un isótopo cinético de deuterio utilizando los cálculos de la teoría funcional de la densidad es ahora relativamente rutinaria. Además, varios modelos cualitativos y semicuantitativos permiten realizar estimaciones aproximadas de los efectos de los isótopos de deuterio sin cálculos, a menudo proporcionando suficiente información para racionalizar los datos experimentales o incluso apoyar o refutar diferentes posibilidades mecánicas. Los materiales de partida que contienen deuterio a menudo están disponibles comercialmente, lo que hace que la síntesis de materiales de partida enriquecidos isotópicamente sea relativamente sencilla. Además, debido a la gran diferencia relativa en la masa de deuterio y protio y las diferencias concomitantes en las frecuencias vibratorias,permitiendo medir e interpretar fácilmente los efectos isotópicos primarios y secundarios. Por el contrario, los efectos secundarios son generalmente muy pequeños para elementos más pesados ​​y de magnitud cercana a la incertidumbre experimental, lo que complica su interpretación y limita su utilidad. En el contexto de los efectos isotópicos, el hidrógeno se usa con frecuencia para referirse específicamente al isótopo ligero, protio (H). En el resto de este artículo, la referencia al hidrógeno y al deuterio en construcciones gramaticales paralelas o las comparaciones directas entre ellas deben interpretarse como referencias al protio y al deuterio.

La teoría de los efectos isotópicos cinéticos fue formulada por primera vez por Jacob Bigeleisen en 1949. A continuación se proporciona la fórmula general de Bigeleisen para los efectos isotópicos cinéticos del deuterio (que también es aplicable a elementos más pesados). Emplea la teoría del estado de transición y un tratamiento mecánico estadístico de los niveles de traslación, rotación y vibración para el cálculo de las constantes de velocidad k _H y k _D. Sin embargo, esta fórmula es "semiclásica" en el sentido de que ignora la contribución de la tunelización cuántica, que a menudo se introduce como un factor de corrección independiente. La fórmula de Bigeleisen tampoco se ocupa de las diferencias en las interacciones repulsivas no enlazadas causadas por el enlace C-D ligeramente más corto en comparación con un enlace C-H. En la ecuación, las cantidades con los subíndices H o D se refieren a las especies sustituidas con hidrógeno o deuterio, respectivamente, mientras que las cantidades con o sin la doble daga, ‡, se refieren al estado de transición o al estado fundamental del reactivo, respectivamente. (En sentido estricto, también debería incluirse un término resultante de una diferencia isotópica en los coeficientes de transmisión).,

donde definimosy .

Aquí, h es la constante de Planck, k _B es la constante de Boltzmann, es la frecuencia de la vibración, expresada en números de onda, c es la velocidad de la luz, N _A es la constante de Avogadro y R es la constante universal de los gases. Los σ _X (X = H o D) son los números de simetría para los reactivos y los estados de transición. Los M _X son las masas moleculares de las especies correspondientes, y los I _{q X} (q = x, y, o z) términos son los momentos de inercia sobre los tres ejes principales. Los u _{i X} son directamente proporcionales a las frecuencias vibratorias correspondientes, ν _i, y la energía vibratoria del punto cero (ver más abajo). Los números enteros N y N son el número de átomos en los reactivos y los estados de transición, respectivamente. La complicada expresión dada arriba se puede representar como el producto de cuatro factores separados:.

Para el caso especial de los efectos del isótopo del deuterio, argumentaremos que los primeros tres términos pueden tratarse como iguales o bien aproximados por la unidad. El primer factor S (que contiene el σ _X) es la relación de los números de simetría para las distintas especies. Este será un número racional (una proporción de números enteros) que depende del número de rotaciones moleculares y de enlaces que conducen a la permutación de átomos o grupos idénticos en los reactivos y el estado de transición. Para sistemas de baja simetría, todo σ _X (reactivo y estado de transición) será la unidad; por lo tanto, a menudo se puede despreciar S. El factor MMI (que contiene el M _X y el I _{q X}) se refiere a la relación de las masas moleculares y los momentos de inercia. Dado que el hidrógeno y el deuterio tienden a ser mucho más livianos en comparación con la mayoría de los reactivos y estados de transición, hay poca diferencia en las masas moleculares y los momentos de inercia entre las moléculas que contienen H y D, por lo que el factor MMI generalmente también se aproxima como unidad. El factor EXC (que contiene el producto de las funciones de partición vibratorias) corrige el efecto del isótopo cinético causado por las reacciones de las moléculas vibratoriamente excitadas. La fracción de moléculas con suficiente energía para tener vibraciones de enlace A–H/D en el estado excitado es generalmente pequeña para reacciones a temperatura ambiente o cerca de ella (los enlaces con el hidrógeno generalmente vibran a 1000 cm o más, por lo que exp(- u _i) = exp(- hν _i / k _B T) < 0,01 a 298 K, lo que resulta en contribuciones insignificantes de los factores 1–exp(- u _i)). Por lo tanto, para los efectos isotópicos cinéticos de hidrógeno/deuterio, los valores observados suelen estar dominados por el último factor, ZPE (una función exponencial de las diferencias de energía de punto cero vibratorio), que consiste en contribuciones de las diferencias de energía de punto cero para cada uno de los factores vibratorios. modos de los reactivos y estado de transición, que se pueden representar de la siguiente manera:,

donde definimosy .

Las sumas en el exponente de la segunda expresión pueden interpretarse como recorriendo todos los modos de vibración del estado fundamental del reactivo y el estado de transición. Alternativamente, uno puede interpretarlos como recorriendo aquellos modos exclusivos del reactivo o del estado de transición o cuyas frecuencias vibratorias cambian sustancialmente al avanzar a lo largo de la coordenada de reacción. Los pares restantes de modos vibracionales de reactivo y estado de transición tienen y cancelaciones muy similares cuando se calculan las sumas en el exponente. Por lo tanto, en la práctica, los KIE de deuterio a menudo dependen en gran medida de un puñado de modos vibratorios clave debido a esta cancelación, lo que hace posible el análisis cualitativo de k _H / k _D.

Como se mencionó, especialmente para la sustitución de hidrógeno/deuterio, la mayoría de los efectos isotópicos cinéticos surgen de la diferencia en la energía de punto cero (ZPE) entre los reactivos y el estado de transición de los isotopólogos en cuestión, y esta diferencia se puede entender cualitativamente con la siguiente descripción: dentro de la aproximación de Born-Oppenheimer, la superficie de energía potencial es la misma para ambas especies isotópicas. Sin embargo, un tratamiento mecánico-cuántico de la energía introduce niveles de vibración discretos en esta curva, y el estado de energía más bajo posible de una molécula corresponde al nivel de energía de vibración más bajo, que es ligeramente más alto en energía que el mínimo de la curva de energía potencial. Esta diferencia, denominada energía de punto cero, es una manifestación del principio de incertidumbre de Heisenberg que requiere una incertidumbre en la longitud del enlace CH o CD. Dado que la especie más pesada (en este caso, la deuterada) se comporta de manera más "clásica", sus niveles de energía vibratoria están más cerca de la curva de energía potencial clásica y tiene una energía de punto cero más baja. Las diferencias de energía de punto cero entre las dos especies isotópicas, al menos en la mayoría de los casos, disminuyen en el estado de transición, ya que la constante de fuerza de enlace disminuye durante la ruptura del enlace. Por lo tanto, la menor energía de punto cero de las especies deuteradas se traduce en una mayor energía de activación para su reacción, como se muestra en la siguiente figura, lo que conduce a un efecto de isótopo cinético normal. sus niveles de energía vibratoria están más cerca de la curva de energía potencial clásica y tiene una energía de punto cero más baja. Las diferencias de energía de punto cero entre las dos especies isotópicas, al menos en la mayoría de los casos, disminuyen en el estado de transición, ya que la constante de fuerza de enlace disminuye durante la ruptura del enlace. Por lo tanto, la menor energía de punto cero de las especies deuteradas se traduce en una mayor energía de activación para su reacción, como se muestra en la siguiente figura, lo que conduce a un efecto de isótopo cinético normal. sus niveles de energía vibratoria están más cerca de la curva de energía potencial clásica y tiene una energía de punto cero más baja. Las diferencias de energía de punto cero entre las dos especies isotópicas, al menos en la mayoría de los casos, disminuyen en el estado de transición, ya que la constante de fuerza de enlace disminuye durante la ruptura del enlace. Por lo tanto, la menor energía de punto cero de las especies deuteradas se traduce en una mayor energía de activación para su reacción, como se muestra en la siguiente figura, lo que conduce a un efecto de isótopo cinético normal.Este efecto debería, en principio, tenerse en cuenta todos los 3 N - 6 modos de vibración para el material de partida y los 3 N - 7 modos de vibración en el estado de transición (falta un modo, el que corresponde a la coordenada de reacción, en el estado de transición). estado, ya que un enlace se rompe y no hay fuerza restauradora contra el movimiento). El oscilador armónico es una buena aproximación para un enlace vibratorio, al menos para estados vibracionales de baja energía. La mecánica cuántica da la energía de punto cero vibracional como . Por lo tanto, podemos interpretar fácilmente el factor de ½ y las sumas detérminos sobre los modos de vibración del estado fundamental y del estado de transición en el exponente de la fórmula simplificada anterior. Para un oscilador armónico, la frecuencia vibratoria es inversamente proporcional a la raíz cuadrada de la masa reducida del sistema vibratorio:,

donde k _f es la constante de fuerza. Además, la masa reducida se aproxima a la masa del átomo ligero del sistema, X = H o D. Como m _D es aproximadamente 2 m _H,.

En el caso de una disociación homolítica del enlace C–H/D, el término del estado de transición desaparece y, despreciando otros modos vibratorios, k _H / k _D = exp(½Δ u _i). Por lo tanto, se observa un efecto isotópico mayor para un enlace C-H/D más rígido ("más fuerte"). Para la mayoría de las reacciones de interés, un átomo de hidrógeno se transfiere entre dos átomos, con un estado de transición [A···H···B] y los modos de vibración en el estado de transición deben tenerse en cuenta. Sin embargo, sigue siendo generalmente cierto que la escisión de un enlace con una frecuencia vibratoria más alta dará un efecto isotópico mayor.

Diferencias de energía ZPE y diferencias correspondientes en las energías de activación para la ruptura de enlaces CH y CD análogos. Tenga en cuenta que en este diagrama esquemático, las curvas en realidad representan hipersuperficies dimensionales (3

N - 6) y (3

N - 7), y que el modo vibratorio cuya ZPE se ilustra en el estado de transición

no es el mismo que el de la reacción. coordinar. La coordenada de reacción representa una vibración con una constante de fuerza negativa (y una frecuencia de vibración imaginaria) para el estado de transición. El ZPE que se muestra para el estado fundamental

puede referirse a la vibración correspondiente a la coordenada de reacción en el caso de un KIE primario.

Para calcular el valor máximo posible para un KIE de deuterio sin túnel, consideramos el caso en el que la diferencia de energía de punto cero entre las vibraciones de estiramiento de un enlace típico carbono-hidrógeno (3000 cm) y un enlace carbono-deuterio (2200 cm) desaparece en el estado de transición (una diferencia de energía de (1/2)(3000 – 2200 cm) = 400 cm, o alrededor de 1,15 kcal/mol), sin ninguna compensación de una diferencia de energía de punto cero en el estado de transición (p. ej., del tramo simétrico A···H···B, que es exclusivo del estado de transición). La fórmula simplificada dada arriba predice un máximo para k _H / k _D como 6.9. Si también se incluye la desaparición completa de dos vibraciones de flexión, k _HSe pueden predecir valores de / k _{D tan grandes como 15-20.} Sin embargo, es muy poco probable que las frecuencias de flexión desaparezcan en el estado de transición, y solo hay unos pocos casos en los que los valores de k _H / k _D superan 7-8 cerca de la temperatura ambiente. Además, a menudo se encuentra que la formación de túneles es un factor importante cuando superan dichos valores. Se cree que un valor de k _H / k _D ~ 10 es el máximo para un efecto de isótopo cinético primario semiclásico (sin efecto túnel) para reacciones que tienen lugar alrededor de 298 K. (La fórmula para k _H / k _Ddepende de la temperatura, por lo que son posibles efectos isotópicos más grandes a temperaturas más bajas). Dependiendo de la naturaleza del estado de transición de la transferencia de H (simétrico frente a "temprano" o "tardío" y lineal frente a doblado), la medida en que un efecto de isótopo de deuterio primario se aproxima a este máximo varía. Un modelo desarrollado por Westheimer predijo que los estados de transición lineales simétricos (termoneutros, según el postulado de Hammond) tienen los mayores efectos isotópicos, mientras que los estados de transición que son "tempranos" o "tardíos" (para reacciones exotérmicas o endotérmicas, respectivamente) o no lineales (por ejemplo, cíclicos) exhiben efectos más pequeños. Desde entonces, estas predicciones han recibido un amplio apoyo experimental.

Para los efectos isotópicos secundarios del deuterio, Streitwieser propuso que el debilitamiento (o el fortalecimiento, en el caso de un efecto isotópico inverso) de los modos de flexión del estado fundamental reactivo al estado de transición son en gran parte responsables de los efectos isotópicos observados. Estos cambios se atribuyen a un cambio en el entorno estérico cuando el carbono unido al H/D sufre una rehibridación de sp a sp o viceversa (un efecto de isótopo cinético secundario α), o al debilitamiento del enlace debido a la hiperconjugación en los casos en que se está produciendo un carbocatión. generó un átomo de carbono de distancia (un efecto de isótopo cinético secundario β). Estos efectos isotópicos tienen un máximo teórico de k _H / k _D = 2≈ 1.4. Para un efecto isotópico cinético secundario en la posición α, la rehibridación de sp a sp produce un efecto isotópico normal, mientras que la rehibridación de sp a sp da como resultado un efecto isotópico inverso con un mínimo teórico de k _H / k _D = 2 ≈ 0,7. En la práctica, k _H / k _D ~ 1.1-1.2 y k _H / k _D ~ 0.8-0.9 son típicos para los efectos isotópicos cinéticos secundarios α, mientras que k _H / k _D~ 1.15-1.3 son típicos para el efecto isotópico cinético secundario β. Para los reactivos que contienen varios átomos de hidrógeno β sustituidos isotópicamente, el efecto isotópico observado es a menudo el resultado de varios H/D en la posición β que actúan en concierto. En estos casos, el efecto de cada átomo marcado isotópicamente es multiplicativo, y no son raros los casos en los que k _H / k _{D > 2.}

Las siguientes expresiones simples que relacionan los efectos isotópicos cinéticos del deuterio y el tritio, que también se conocen como la ecuación de Swain (o las ecuaciones de Swain-Schaad-Stivers), se pueden derivar de la expresión general dada anteriormente usando algunas simplificaciones:;

es decir,.

Al derivar estas expresiones, se utilizó la aproximación razonable de que las masas reducidas son aproximadamente iguales a las masas del hidrógeno, el deuterio o el tritio. Además, se supuso que el movimiento vibratorio se aproximaba mediante un oscilador armónico, de modo que (X = H, D o T). El subíndice " s " se refiere a estos efectos isotópicos cinéticos "semiclásicos", que ignoran el túnel cuántico. Las contribuciones de túneles deben tratarse por separado como un factor de corrección.

Para los efectos isotópicos que involucran elementos distintos al hidrógeno, muchas de estas simplificaciones no son válidas y la magnitud del efecto isotópico puede depender en gran medida de algunos o todos los factores ignorados. Por lo tanto, los efectos isotópicos cinéticos para elementos distintos del hidrógeno suelen ser mucho más difíciles de racionalizar o interpretar. En muchos casos, y especialmente para las reacciones de transferencia de hidrógeno, las contribuciones a los efectos isotópicos cinéticos de la formación de túneles son significativas (ver más abajo).

Tunelización

En algunos casos, se observa una mejora de la tasa adicional para el isótopo más ligero, posiblemente debido a la tunelización de la mecánica cuántica. Esto normalmente solo se observa para reacciones que involucran enlaces a átomos de hidrógeno. La tunelización ocurre cuando una molécula penetra a través de una barrera de energía potencial en lugar de atravesarla. Aunque las leyes de la mecánica clásica no lo permiten, las partículas pueden pasar a través de regiones del espacio clásicamente prohibidas en la mecánica cuántica basada en la dualidad onda-partícula.

El análisis de la tunelización se puede realizar utilizando la modificación de Bell de la ecuación de Arrhenius, que incluye la adición de un factor de tunelización, Q:

donde A es el parámetro de Arrhenius, E es la altura de la barrera y

donde y

El examen del término β muestra una dependencia exponencial de la masa de la partícula. Como resultado, la formación de túneles es mucho más probable para una partícula más ligera como el hidrógeno. El simple hecho de duplicar la masa de un protón de túnel reemplazándolo con su isótopo deuterio reduce drásticamente la velocidad de tales reacciones. Como resultado, se observan efectos isotópicos cinéticos muy grandes que no pueden explicarse por las diferencias en las energías de punto cero.

Modelo Donante-Aceptor de una transferencia de protones.

Además, el término β depende linealmente del ancho de la barrera, 2a. Al igual que con la masa, la formación de túneles es mayor para anchos de barrera pequeños. La distancia óptima de tunelización de protones entre el átomo donante y el aceptor es de 0,4 Å.

mostrarDependencia de la temperatura en la tunelización

mostrarCriterios para la tunelización KIE

mostrarEjemplos de tunelización en KIE

Efecto isotópico cinético transitorio

El efecto isotópico expresado con las ecuaciones dadas anteriormente solo se refiere a reacciones que pueden describirse con cinética de primer orden. En todos los casos en los que esto no sea posible, los efectos isotópicos cinéticos transitorios deben tenerse en cuenta utilizando las ecuaciones GEBIK y GEBIF.

Experimentos

Simmons y Hartwig se refieren a los siguientes tres casos como los principales tipos de experimentos de efectos isotópicos cinéticos que involucran la funcionalización del enlace CH:A) KIE determinado a partir de tasas absolutas de dos reacciones paralelas

En este experimento, las constantes de velocidad para el sustrato normal y su análogo marcado isotópicamente se determinan de forma independiente y el KIE se obtiene como una relación de los dos. La precisión del KIE medido está severamente limitada por la precisión con la que se puede medir cada una de estas constantes de velocidad. Además, reproducir las condiciones exactas en las dos reacciones paralelas puede resultar muy complicado. Sin embargo, una medición de un gran efecto isotópico cinético a través de la comparación directa de las constantes de velocidad es indicativa de que la escisión del enlace CH se produce en el paso determinante de la velocidad. (Un valor menor podría indicar un efecto isotópico debido a un preequilibrio, de modo que la escisión del enlace CH ocurre en algún lugar antes del paso que determina la velocidad).B) KIE determinado a partir de una competencia intermolecular

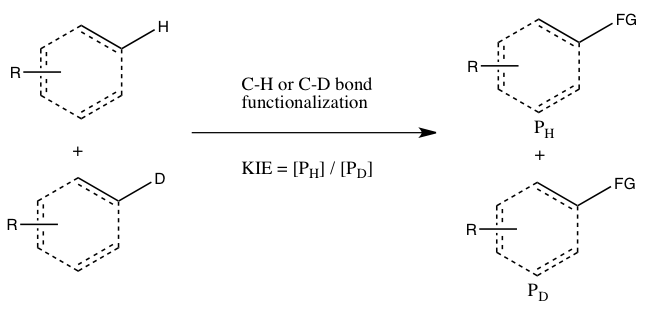
En este tipo de experimento, se emplean los mismos sustratos que se usan en el Experimento A, pero se les permite reaccionar en el mismo recipiente, en lugar de dos recipientes separados. El efecto del isótopo cinético de este experimento está determinado por la cantidad relativa de productos formados a partir de la funcionalización de CH versus CD (o puede deducirse de las cantidades relativas de materiales de partida sin reaccionar). Es necesario extinguir la reacción antes de que se complete para observar el efecto del isótopo cinético (consulte la sección Evaluación a continuación). En general, la reacción se detiene con una conversión baja (de ~5 a 10 % de conversión) o se usa un gran exceso (> 5 equiv.) de la mezcla isotópica. Este tipo de experimento asegura que las funcionalizaciones de enlaces CH y CD ocurran exactamente bajo las mismas condiciones, y la proporción de productos de las funcionalizaciones de enlaces CH y CD se puede medir con mucha mayor precisión que las constantes de velocidad en el Experimento A. Además, solo se requiere una sola medición de las concentraciones de productos de una sola muestra. Sin embargo, un efecto de isótopo cinético observado en este experimento es más difícil de interpretar, ya que puede significar que la escisión del enlace CH ocurre durante el paso determinante de la velocidad o en un paso determinante del producto que sigue al paso determinante de la velocidad. No obstante, la ausencia de un efecto de isótopo cinético, al menos según Simmons y Hartwig, es indicativa de que la escisión del enlace CH no se produce durante el paso de determinación de la velocidad. solo se requiere una sola medición de las concentraciones del producto de una sola muestra. Sin embargo, un efecto de isótopo cinético observado en este experimento es más difícil de interpretar, ya que puede significar que la escisión del enlace CH ocurre durante el paso determinante de la velocidad o en un paso determinante del producto que sigue al paso determinante de la velocidad. No obstante, la ausencia de un efecto de isótopo cinético, al menos según Simmons y Hartwig, es indicativa de que la escisión del enlace CH no se produce durante el paso de determinación de la velocidad. solo se requiere una sola medición de las concentraciones del producto de una sola muestra. Sin embargo, un efecto de isótopo cinético observado en este experimento es más difícil de interpretar, ya que puede significar que la escisión del enlace CH ocurre durante el paso determinante de la velocidad o en un paso determinante del producto que sigue al paso determinante de la velocidad. No obstante, la ausencia de un efecto de isótopo cinético, al menos según Simmons y Hartwig, es indicativa de que la escisión del enlace CH no se produce durante el paso de determinación de la velocidad.C) KIE determinado a partir de una competencia intramolecular

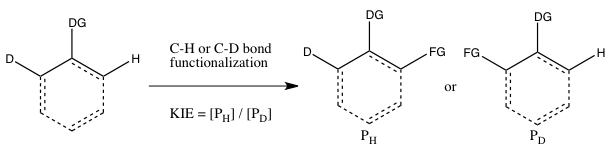
Este tipo de experimento es análogo al Experimento B, excepto que esta vez hay una competencia intramolecular por la funcionalización del enlace CH o CD. En la mayoría de los casos, el sustrato posee un grupo director (DG) entre los enlaces CH y CD. El cálculo del efecto isotópico cinético de este experimento y su interpretación siguen las mismas consideraciones que las del Experimento B. Sin embargo, los resultados de los Experimentos B y C diferirán si la unión irreversible del sustrato que contiene isótopos tiene lugar en el Experimento B antesa la escisión del enlace CH o CD. En tal escenario, se puede observar un efecto de isótopo en el Experimento C (donde la elección del isótopo puede tener lugar incluso después de la unión del sustrato) pero no en el Experimento B (dado que la elección de si el enlace CH o CD se escinde ya se hace tan pronto como el sustrato se une irreversiblemente). A diferencia del Experimento B, no es necesario detener la reacción con un bajo consumo de material de partida isotópico para obtener un k _H / k _D preciso, ya que la relación de H y D en el material de partida es 1:1, independientemente de la grado de conversión.

Un ejemplo de activación sin CH de diferentes efectos isotópicos observados en el caso de competencia intermolecular (Experimento B) e intramolecular (Experimento C) es la fotólisis de difenildiazometano en presencia de t -butilamina. Para explicar este resultado, se propuso la formación de difenilcarbeno, seguida de un ataque nucleofílico irreversible por parte de la t -butilamina. Debido a que hay poca diferencia isotópica en la tasa de ataque nucleofílico, el experimento intermolecular resultó en un KIE cercano a 1. Sin embargo, en el caso intramolecular, la relación de producto está determinada por la transferencia de protones que ocurre después del ataque nucleofílico, un proceso para que hay un KIE sustancial de 2.6.

Por lo tanto, los Experimentos A, B y C darán resultados de diferentes niveles de precisión y requerirán diferentes configuraciones experimentales y formas de analizar los datos. Como resultado, la viabilidad de cada tipo de experimento dependerá del perfil cinético y estequiométrico de la reacción, así como de las características físicas de la mezcla de reacción (p. ej., homogénea frente a heterogénea). Además, como se señaló en el párrafo anterior, los experimentos proporcionan datos del efecto isotópico cinético para diferentes pasos de una reacción de múltiples pasos, según las ubicaciones relativas del paso limitante de la velocidad, los pasos determinantes del producto y/o la escisión de CH/D. paso.

Los ejemplos hipotéticos a continuación ilustran escenarios comunes. Considere el siguiente diagrama de coordenadas de reacción. Para una reacción con este perfil, los tres experimentos (A, B y C) producirán un efecto isotópico cinético primario significativo:

Perfil de energía de reacción para cuando ocurre la escisión de CH en el RDS

Por otro lado, si una reacción sigue el siguiente perfil de energía, en el que la escisión del enlace CH o CD es irreversible pero ocurre después del paso determinante de la velocidad (RDS), no se observará un efecto isotópico cinético significativo con el Experimento A, ya que el la tasa global no se ve afectada por la sustitución isotópica. Sin embargo, el paso irreversible de escisión del enlace CH dará un efecto de isótopo cinético primario con los otros dos experimentos, ya que el segundo paso todavía afectaría la distribución del producto. Por lo tanto, con los Experimentos B y C, es posible observar el efecto del isótopo cinético incluso si la escisión del enlace CH o CD no ocurre en el paso determinante de la velocidad, sino en el paso determinante del producto.

Perfil de energía de reacción para cuando se produce la escisión del enlace CH en un paso determinante del producto después del RDS

mostrarEvaluación de los efectos de los isótopos cinéticos en una reacción hipotética de varios pasos

Evaluación de relaciones de constantes de velocidad de reacciones de competencia intermolecular

En las reacciones de competición, el efecto isotópico cinético se calcula a partir de las proporciones del producto isotópico o del reactivo restante después de la reacción, pero estas proporciones dependen en gran medida del grado de finalización de la reacción. Más comúnmente, el sustrato isotópico consistirá en moléculas marcadas en una posición específica y sus contrapartes ordinarias no marcadas. También es posible en el caso de los efectos isotópicos cinéticos C, así como en casos similares, confiar simplemente en la abundancia natural del carbono isotópico para los experimentos de efectos isotópicos cinéticos, eliminando la necesidad de etiquetado isotópico. Los dos sustratos isotópicos reaccionarán a través del mismo mecanismo, pero a velocidades diferentes. La relación entre las cantidades de las dos especies en los reactivos y los productos cambiará gradualmente en el transcurso de la reacción, y este cambio gradual se puede tratar de la siguiente manera: suponga que dos moléculas isotópicas, A ₁ y A ₂, sufrir reacciones de competencia irreversibles de la siguiente manera:

Se encuentra que el efecto isotópico cinético para este escenario es:

Donde F ₁ y F ₂ se refieren a la fracción de conversiones para las especies isotópicas A ₁ y A ₂, respectivamente.

mostrarEvaluación

mostrarMedición de F

₁ en términos de pesos por unidad de volumen o molaridades de los reactivos

El enriquecimiento isotópico del material de partida se puede calcular a partir de la dependencia de R/R ₀ de F ₁ para varios efectos isotópicos cinéticos, dando la siguiente figura. Debido a la dependencia exponencial, incluso los efectos isotópicos cinéticos muy bajos conducen a grandes cambios en la composición isotópica del material de partida a altas conversiones.

El enriquecimiento isotópico de la cantidad relativa de la especie 2 con respecto a la especie 1 en el material de partida en función de la conversión de la especie 1. El valor del efecto isotópico cinético (

k ₁ /

k ₂) se indica en cada curva.

Cuando se siguen los productos, el efecto del isótopo cinético se puede calcular utilizando la relación de productos R _P junto con R ₀ de la siguiente manera:

Medición del efecto isotópico cinético en abundancia natural

La medición del efecto isotópico cinético en abundancia natural es un método general simple para medir los efectos isotópicos cinéticos (KIE) para reacciones químicas realizadas con materiales de abundancia natural. Esta técnica para medir KIE supera muchas limitaciones de los métodos de medición de KIE anteriores. Las mediciones KIE de materiales marcados isotópicamente requieren una nueva síntesis para cada material marcado isotópicamente (un proceso a menudo prohibitivamente difícil), una reacción competitiva y un análisis.La medición KIE en abundancia natural evita estos problemas al aprovechar las técnicas cuantitativas de alta precisión (espectroscopia de resonancia magnética nuclear, espectrometría de masas de relación isotópica) para medir de forma selectiva el fraccionamiento cinético de isótopos, ya sea en el producto o en el material de partida para una reacción química determinada.

RMN de un solo pulso

La espectroscopia de resonancia magnética nuclear (RMN) cuantitativa de un solo pulso es un método apto para medir el fraccionamiento cinético de isótopos para mediciones de KIE de abundancia natural. Pascual et al. se inspiraron en estudios que demostraron variaciones dramáticas de deuterio dentro de compuestos idénticos de diferentes fuentes y plantearon la hipótesis de que la RMN podría usarse para medir los efectos de los isótopos cinéticos del deuterio en abundancia natural. Pascal y sus compañeros de trabajo probaron su hipótesis estudiando la reacción de inserción del diazomalonato de dimetilo en el ciclohexano. Pascual et al. midió un KIE de 2.2 usandoHRMN para materiales de abundancia natural.

Singleton y colaboradores demostraron la capacidad deCMediciones KIE de abundancia natural basadas en RMN para estudiar el mecanismo de la cicloadición [4 + 2] de isopreno con anhídrido maleico. Estudios previos de Gajewski sobre materiales enriquecidos isotópicamente observaron resultados de KIE que sugerían un estado de transición asíncrono, pero siempre fueron consistentes, dentro del margen de error, para un mecanismo de reacción perfectamente sincrónico.

Este trabajo de Singleton et al. estableció la medición de múltiplesCKIE está dentro del diseño de un solo experimento. EstasHyCLas mediciones de KIE determinadas en abundancia natural encontraron que los hidrógenos "interiores" del dieno experimentan un cambio más pronunciadoHKIE que los hidrógenos "externos" y el C1 y C4 experimentan un KIE significativo. Estas observaciones clave sugieren un mecanismo de reacción asíncrono para la cicloadición de isopreno con anhídrido maleico.

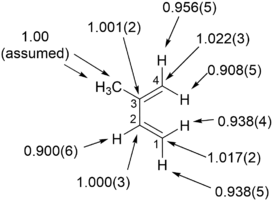
Las limitaciones para determinar los KIE en abundancia natural usando RMN son que el material recuperado debe tener una cantidad y pureza adecuadas para el análisis de RMN (la señal de interés debe ser distinta de otras señales), la reacción de interés debe ser irreversible y el mecanismo de reacción no debe cambiar durante la duración de la reacción química.

Detalles experimentales para usar RMN cuantitativa de un solo pulso para medir el efecto isotópico cinético en abundancia natural de la siguiente manera: el experimento debe realizarse en condiciones cuantitativas que incluyan un tiempo de relajación de 5 T _1, un ángulo de giro de 90° medido, una resolución digital de al menos 5 puntos a través de un pico y una señal: ruido superior a 250. El FID sin procesar se rellena con ceros hasta al menos 256 000 puntos antes de la transformada de Fourier. Los espectros de RMN se escalonan y luego se tratan con una corrección de línea de base de orden cero sin ninguna corrección de inclinación. Las integraciones de señales se determinan numéricamente con una tolerancia mínima para cada señal integrada.

Ejemplos de elucidación del mecanismo de reacción organometálica

Colletto et al. desarrolló una arilación regioselectiva de benzo[b]tiofenos a temperatura ambiente con yoduros de arilo como compañeros de acoplamiento y buscó comprender el mecanismo de esta reacción mediante la realización de mediciones del efecto isotópico cinético de abundancia natural a través de RMN de pulso único.

Arilación

regioselectiva de benzo[b]tiofenos

H KIE medidos en abundancia natural

C KIE medidos en abundancia natural

La observación de un efecto de isótopo de C primario en C3, un efecto de isótopo de H inverso, un efecto de isótopo de C secundario en C2 y la falta de un efecto de isótopo de H en C2 conducen a Colletto et al. sugerir un mecanismo de reacción tipo Heck para la arilación regioselectiva de benzo[b]tiofenos a temperatura ambiente con yoduros de arilo como compañeros de acoplamiento.

Frost et al. buscó comprender los efectos de los aditivos de ácido de Lewis en el mecanismo de activación del enlace CN catalizada por paladio enantioselectiva utilizando mediciones del efecto isotópico cinético de abundancia natural a través de RMN de pulso único.

Cianoamidación de alquenos intramolecular enantioselectiva

13C KIE para la reacción de cianoamidación de alqueno intramolecular enantioselectiva (a la izquierda sin aditivo, a la derecha agregar BPh

₃)

El efecto del isótopo cinético C primario observado en ausencia de BPh ₃ sugiere un mecanismo de reacción con oxidación cis limitante de la velocidad en el enlace C-CN de la cianoformamida. La adición de BPh ₃ provoca una disminución relativa en el efecto del isótopo cinético C observado, lo que llevó a Frost et al. sugerir un cambio en el paso limitante de la velocidad de la oxidación cis a la coordinación del paladio a la cianoformamida.

RMN DEPT-55

Aunque las mediciones del efecto isotópico cinético en abundancia natural son una herramienta poderosa para comprender los mecanismos de reacción, las cantidades de material requeridas para el análisis pueden hacer que esta técnica sea inaccesible para reacciones que emplean reactivos costosos o materiales de partida inestables. Para mitigar estas limitaciones, Jacobsen y sus colaboradores desarrollaron la transferencia de polarización de H a C como un medio para reducir el tiempo y el material necesarios para las mediciones del efecto isotópico cinético en abundancia natural. La mejora sin distorsión por transferencia de polarización (DEPT) aprovecha la relación giromagnética más grande de H sobreC para mejorar teóricamente la sensibilidad de la medición en un factor de 4 o reducir el tiempo del experimento en un factor de 16. Este método para la medición de isótopos cinéticos de abundancia natural es favorable para el análisis de reacciones que contienen materiales de partida inestables y catalizadores o productos que son relativamente costosos.

Jacobsen y colaboradores identificaron la glicosilación de galactosa catalizada por tiourea como una reacción que cumplía con los dos criterios antes mencionados (materiales costosos y sustratos inestables) y era una reacción con un mecanismo poco conocido. La glicosilación es un caso especial de sustitución nucleófila que carece de una definición clara entre el carácter mecanístico de S _N 1 y S _{N 2.} La presencia del oxígeno adyacente al sitio de desplazamiento (es decir, C1) puede estabilizar la carga positiva. Esta estabilización de carga puede hacer que cualquier vía concertada potencial se vuelva asíncrona y se acerque a los intermedios con carácter de oxocarbenio del mecanismo S _N 1 para la glicosilación.

Esquema de reacción para la glicosilación de galactosa catalizada por tiourea

Mediciones del efecto del isótopo cinético C para la glicosilación de galactosa catalizada por tiourea

Jacobsen y colaboradores observaron pequeños KIE normales en C1, C2 y C5, lo que sugiere un carácter significativo de oxocarbenio en el estado de transición y un mecanismo de reacción asíncrono con un alto grado de separación de carga.

Espectrometría de masas de relación isotópica

La espectrometría de masas de relación isotópica de alta precisión (IRMS) es otro método para medir el fraccionamiento cinético de isótopos para mediciones de KIE de abundancia natural. Widlanski y colaboradores demostraronSKIE en medidas de abundancia natural para la hidrólisis de monoésteres de sulfato. Su observación de un KIE grande sugiere que la escisión del enlace SO controla la velocidad y probablemente descarta un mecanismo de reacción asociado.

Efecto del isótopo 34S en la reacción de hidrólisis del éster de sulfato

La principal limitación para determinar los KIE en abundancia natural usando IRMS es la degradación selectiva del sitio requerida sin fraccionamiento isotópico en una molécula pequeña analizable, una tarea no trivial.

Estudios de caso

Efectos primarios de isótopos de hidrógeno

Los efectos isotópicos cinéticos del hidrógeno primario se refieren a casos en los que se forma o rompe un enlace con el hidrógeno marcado isotópicamente en un paso de una reacción que determina la velocidad y/o el producto.Estos son los efectos isotópicos cinéticos medidos con mayor frecuencia, y gran parte de la teoría cubierta anteriormente se refiere a los efectos isotópicos cinéticos primarios. Cuando hay evidencia adecuada de que la transferencia del hidrógeno marcado ocurre en el paso de determinación de la velocidad de una reacción, si se observa un efecto isotópico cinético bastante grande, por ejemplo, kH/kD de al menos 5-6 o kH/kT alrededor de 10-13 a temperatura ambiente, es bastante probable que la transferencia de hidrógeno sea lineal y que el hidrógeno se encuentre bastante simétricamente ubicado en el estado de transición. Por lo general, no es posible hacer comentarios sobre las contribuciones de los túneles al efecto isotópico observado a menos que el efecto sea muy grande. Si el efecto del isótopo cinético primario no es tan grande, generalmente se considera que es indicativo de una contribución significativa del movimiento del átomo pesado a la reacción coordinada,

Efectos de isótopos de hidrógeno secundarios

Los efectos del isótopo de hidrógeno secundario o el efecto del isótopo cinético secundario (SKIE) surgen en los casos en que la sustitución isotópica está alejada de la ruptura del enlace. El átomo remoto, sin embargo, influye en las vibraciones internas del sistema que, a través de cambios en la energía de punto cero (ZPE), afectan las velocidades de las reacciones químicas. Dichos efectos se expresan como proporciones de la tasa del isótopo ligero a la del isótopo pesado y pueden ser efectos "normales" (la proporción es mayor o igual a 1) o efectos "inversos" (la proporción es menor que 1). Los SKIE se definen como efectos isotópicos secundarios α, β (etc.) donde dichos prefijos se refieren a la posición de la sustitución isotópica en relación con el centro de reacción (ver carbono alfa y beta).El prefijo α se refiere al isótopo asociado con el centro de reacción, mientras que el prefijo β se refiere al isótopo asociado con un átomo vecino al centro de reacción y así sucesivamente.

En química orgánica física, SKIE se analiza en términos de efectos electrónicos como la inducción, la hibridación de enlaces o la hiperconjugación. Estas propiedades están determinadas por la distribución de electrones y dependen de la longitud y los ángulos de enlace promediados por vibración que no se ven muy afectados por la sustitución isotópica. Por lo tanto, se desaconseja el uso del término "efecto de isótopo electrónico", aunque sea legítimo, ya que puede malinterpretarse para sugerir que el efecto de isótopo es de naturaleza electrónica en lugar de vibracional.

Los SKIE pueden explicarse en términos de cambios en la hibridación orbital. Cuando la hibridación de un átomo de carbono cambia de sp a sp, se ven afectados varios modos de vibración (estiramientos, flexión en el plano y fuera del plano). La flexión en el plano y fuera del plano en un carbono con hibridación sp es similar en frecuencia debido a la simetría de un carbono con hibridación sp. En un carbono hibridado sp, la curvatura en el plano es mucho más rígida que la curvatura fuera del plano, lo que da como resultado una gran diferencia en la frecuencia, la ZPE y, por lo tanto, el SKIE (que existe cuando hay una diferencia en la ZPE del reactivo). y estado de transición). El cambio máximo teórico causado por la diferencia de frecuencia de flexión se ha calculado como 1,4.

Cuando el carbono sufre una reacción que cambia su hibridación de sp a sp, la constante de fuerza de flexión fuera del plano en el estado de transición es más débil, ya que está desarrollando un carácter sp y se observa un SKIE "normal" con valores típicos de 1,1 a 1,2. Por el contrario, cuando la hibridación del carbono cambia de sp a sp, las constantes de fuerza de flexión fuera del plano en el estado de transición aumentan y se observa un SKIE inverso con valores típicos de 0,8 a 0,9.

De manera más general, el SKIE para reacciones reversibles puede ser "normal" en un sentido e "inverso" en el otro si la unión en el estado de transición tiene una rigidez intermedia entre el sustrato y el producto, o pueden ser "normales" en ambos sentidos si la unión es más débil en el estado de transición. estado de transición, o "inverso" en ambos sentidos si el enlace es más fuerte en el estado de transición que en cualquiera de los reactivos.

Un ejemplo de un efecto de isótopo cinético secundario α "inverso" se puede ver en el trabajo de Fitzpatrick y Kurtz, quienes utilizaron dicho efecto para distinguir entre dos vías propuestas para la reacción de la d-aminoácido oxidasa con aniones de nitroalcano. La ruta A implicaba un ataque nucleofílico sobre la coenzima FAD, mientras que la ruta B implicaba un intermediario de radicales libres. Como el camino A da como resultado la hibridación intermedia de cambio de carbono de sp a sp, se espera un SKIE "inverso". Si ocurre la ruta B, entonces no se debe observar SKIE ya que el intermediario de radicales libres no cambia la hibridación. Se observó un SKIE de 0,84 y se verificó el Camino A como se muestra en el siguiente esquema.

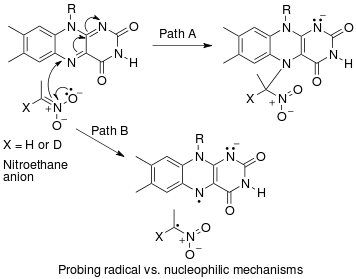
Otro ejemplo de SKIE es la oxidación de alcoholes bencílicos por dimetildioxirano donde se propusieron tres estados de transición para diferentes mecanismos. Nuevamente, al considerar cómo y si los átomos de hidrógeno estaban involucrados en cada uno, los investigadores predijeron si esperarían o no un efecto de sustitución isotópica de ellos. Luego, el análisis de los datos experimentales de la reacción les permitió elegir qué vía era más probable en función del efecto del isótopo observado.

Los efectos secundarios del isótopo de hidrógeno de los hidrógenos de metileno también se usaron para mostrar que la transposición de Cope en 1,5-hexadieno sigue una vía de transposición de enlace concertada, y no una de las vías de radical alilo o 1,4-diilo propuestas alternativamente, todas las cuales son presentado en el siguiente esquema.

Mecanismos alternativos para el reordenamiento de Cope del 1,5-hexadieno: (de arriba a abajo), vías de radicales alilo, concertadas sincrónicas y 1,4-dyil. Se encuentra que la vía predominante es la del medio, que tiene seis electrones π deslocalizados correspondientes a un intermedio aromático.

Efectos isotópicos estéricos

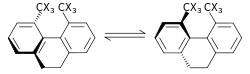
El efecto isotópico estérico es un SKIE que no implica la ruptura o formación de enlaces. Este efecto se atribuye a las diferentes amplitudes vibratorias de los isotopólogos. Un ejemplo de tal efecto es la racemización de 9,10-dihidro-4,5-dimetilfenantreno.La menor amplitud de vibración para el deuterio en comparación con el hidrógeno en los enlaces C-H (carbono-hidrógeno), C-D (carbono-deuterio) da como resultado un radio de van der Waals más pequeño o un tamaño efectivo además de una diferencia en la ZPE entre los dos. Cuando hay una mayor cantidad efectiva de moléculas que contienen una sobre la otra, esto puede manifestarse por un efecto estérico en la constante de velocidad. Para el ejemplo anterior, el deuterio se racemiza más rápido que el isotopólogo del hidrógeno, lo que da como resultado un efecto de isótopo estérico. Bartell desarrolló un modelo para el efecto isotópico estérico. Un efecto de isótopo estérico suele ser pequeño, a menos que las transformaciones pasen por un estado de transición con un grave impedimento estérico, como en el proceso de racemización que se muestra arriba.

Otro ejemplo del efecto isotópico estérico es la reacción de deslizamiento de los rotaxanos. El isótopo deuterio, debido a su tamaño efectivo más pequeño, permite un paso más fácil de los tapones a través del macrociclo, lo que da como resultado tasas más rápidas de deslizamiento para los rotaxanos deuterados.

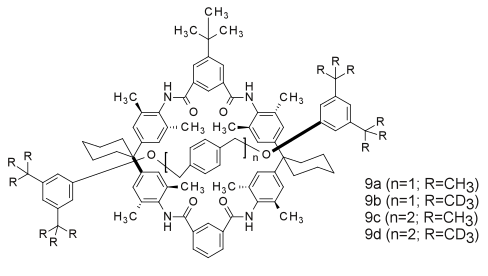
Efectos isotópicos cinéticos inversos

Se conocen reacciones en las que la especie deuterada reacciona más rápido que el análogo no deuterado, y se dice que estos casos exhiben efectos isotópicos cinéticos inversos (IKIE). Los IKIE se observan a menudo en la eliminación reductora de hidruros de metales alquílicos, por ejemplo (Me ₂ NCH ₂ CH ₂ NMe ₂)PtMe(H). En tales casos, el enlace CD en el estado de transición, una especie agóstica, está muy estabilizado en relación con el enlace C-H.

También puede ocurrir un efecto inverso en una reacción de varios pasos si la constante de velocidad general depende de un preequilibrio anterior al paso determinante de la velocidad que tiene un efecto de isótopo de equilibrio inverso. Por ejemplo, las velocidades de las reacciones catalizadas por ácido suelen ser 2-3 veces mayores para las reacciones en D ₂ O catalizadas por D ₃ O que para las reacciones análogas en H ₂ O catalizadas por H ₃ O. Esto puede explicarse por un mecanismo de catálisis específica de iones de hidrógeno de un reactivo R por H ₃ O (o D ₃ O).H ₃ O + R ⇌ RH + H ₂ ORH + H ₂ O → H ₃ O + P

La tasa de formación de productos es entonces d[P]/dt = k ₂ [RH ] = k ₂ K ₁ [H ₃ O ][R] = k _obs [H ₃ O ][R]. En el primer paso, el H ₃ O suele ser un ácido más fuerte que la RH. La deuteración desplaza el equilibrio hacia la especie ácida RD más fuertemente unida, en la que el efecto de la deuteración sobre la energía vibratoria de punto cero es mayor, de modo que la constante de equilibrio deuterada K _1D es mayor que K _1H. Este efecto isotópico de equilibrio en el primer paso generalmente supera el efecto isotópico cinético en el segundo paso, de modo que hay un efecto isotópico inverso aparente y la constante de velocidad global observada k _obs = k ₂ K ₁ disminuye.

Efectos isotópicos cinéticos del hidrógeno solvente

Para que los efectos de los isótopos del solvente sean medibles, una fracción finita del solvente debe tener una composición isotópica diferente al resto. Por lo tanto, deben estar disponibles grandes cantidades de las especies isotópicas menos comunes, lo que limita los efectos isotópicos del solvente observables a las sustituciones isotópicas que involucran hidrógeno. Los efectos isotópicos cinéticos detectables ocurren solo cuando los solutos intercambian hidrógeno con el solvente o cuando hay una interacción soluto-solvente específica cerca del sitio de reacción. Ambos fenómenos son comunes para los disolventes próticos, en los que el hidrógeno es intercambiable, y pueden formar interacciones dipolo-dipolo o enlaces de hidrógeno con moléculas polares.

Efectos de los isótopos de carbono-13

La mayoría de las reacciones orgánicas involucran la ruptura y formación de enlaces a un carbono; por lo tanto, es razonable esperar efectos de isótopos de carbono detectables. Sin embargo, cuando se usa C como etiqueta, el cambio en la masa del isótopo es solo ~ 8%, lo que limita los efectos isotópicos cinéticos observables a valores mucho más pequeños que los observables con los efectos isotópicos de hidrógeno.

Compensar las variaciones en la abundancia natural de C

A menudo, la mayor fuente de error en un estudio que depende de la abundancia natural de carbono es la ligera variación en la propia abundancia natural de C. Tales variaciones surgen porque los materiales de partida utilizados en la reacción son en sí mismos productos de otras reacciones que tienen efectos isotópicos cinéticos y los correspondientes enriquecimientos isotópicos en los productos. Para compensar este error cuando se utiliza la espectroscopia de RMN para determinar el efecto isotópico cinético, se han propuesto las siguientes directrices:

• Elija un carbono que esté alejado del centro de reacción que servirá como referencia y suponga que no tiene un efecto de isótopo cinético en la reacción.
• En el material de partida que no ha sufrido ninguna reacción, determine las proporciones de las otras integrales de los picos de RMN de carbono con respecto a la del carbono de referencia.
• Obtenga las mismas proporciones para los carbonos en una muestra del material de partida después de haber sufrido alguna reacción.
• Las proporciones de las últimas proporciones a las antiguas proporciones R/R ₀.

Si se siguen estas y algunas otras precauciones enumeradas por Jankowski, se pueden lograr efectos de isótopos cinéticos con precisiones de tres decimales.

Efectos isotópicos con elementos más pesados ​​que el carbono

La interpretación de los efectos de los isótopos de carbono suele complicarse al formar y romper simultáneamente enlaces con el carbono. Incluso las reacciones que involucran solo la escisión de enlaces del carbono, como las reacciones S _N 1, implican el fortalecimiento de los enlaces restantes con el carbono. En muchas de estas reacciones, los efectos isotópicos del grupo saliente tienden a ser más fáciles de interpretar. Por ejemplo, las reacciones de sustitución y eliminación en las que el cloro actúa como grupo saliente son convenientes de interpretar, especialmente porque el cloro actúa como una especie monoatómica sin enlaces internos para complicar la reacción coordinada, y tiene dos isótopos estables, Cl y Cl, ambos con alta abundancia. El mayor desafío para la interpretación de tales efectos isotópicos es la solvatación del grupo saliente.

Debido a las incertidumbres experimentales, la medición del efecto isotópico puede implicar una incertidumbre significativa. A menudo, los efectos de los isótopos se determinan mediante estudios complementarios sobre una serie de isotopómeros. En consecuencia, es bastante útil combinar los efectos de los isótopos de hidrógeno con los efectos de los isótopos de átomos pesados. Por ejemplo, se utilizó la determinación del efecto del isótopo de nitrógeno junto con el efecto del isótopo de hidrógeno para mostrar que la reacción del ion 2-feniletiltrimetilamonio con etóxido en etanol a 40 °C sigue un mecanismo E2, a diferencia de los mecanismos alternativos no concertados. Se llegó a esta conclusión al demostrar que esta reacción produce un efecto de isótopo de nitrógeno, k ₁₄ / k ₁₅, de 1.0133±0.0002 junto con un efecto de isótopo cinético de hidrógeno de 3.2 en el hidrógeno saliente.

De manera similar, se utilizó la combinación de los efectos de los isótopos de nitrógeno e hidrógeno para demostrar que las eliminaciones de syn de las sales de amonio simples también siguen un mecanismo concertado, que antes era una cuestión de debate. En las siguientes dos reacciones del ión 2-fenilciclopentiltrimetilamonio con etóxido, ambas de las cuales producen 1-fenilciclopenteno, ambos isómeros exhibieron un efecto de isótopo de nitrógeno k ₁₄ / k ₁₅ a 60 °C. Aunque la reacción del isómero trans, que sigue a la eliminación syn, tiene un efecto de isótopo cinético de nitrógeno más pequeño (1,0064) en comparación con el isómero cis que sufre eliminación anti (1,0108), ambos resultados son lo suficientemente grandes como para indicar el debilitamiento del enlace CN. en el estado de transición que ocurriría en un proceso concertado.

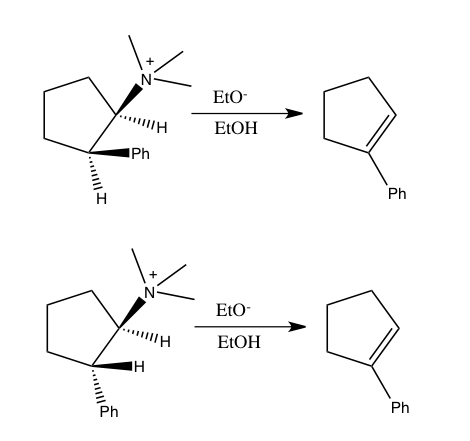
Otros ejemplos

Dado que los efectos isotópicos cinéticos surgen de diferencias en las masas isotópicas, los efectos isotópicos cinéticos observables más grandes están asociados con sustituciones isotópicas de hidrógeno con deuterio (aumento de masa del 100 %) o tritio (aumento de masa del 200 %). Los efectos de los isótopos cinéticos de las proporciones de masas isotópicas pueden ser tan grandes como 36,4 usando muones. Han producido el átomo de hidrógeno más ligero, H (0,113 amu), en el que un electrón orbita alrededor de un "núcleo" de muón positivo (μ) que tiene una masa de 206 electrones. También han preparado el análogo del átomo de hidrógeno más pesado reemplazando un electrón en helio con un muón negativo (μ) para formar Heμ con una masa atómica de 4.116 amu. Dado que el muón negativo es mucho más pesado que un electrón, orbita mucho más cerca del núcleo, protegiendo efectivamente a un protón, lo que hace que Heμ se comporte como H. Con estas especies exóticas, se investigó la reacción de H con H _2. Las constantes de velocidad de la reacción de los análogos de hidrógeno más ligeros y más pesados ​​con H ₂ se utilizaron para calcular el efecto isotópico cinético k _0,11 / k _4,1, en el que hay una diferencia de 36,4 veces en las masas isotópicas. Para esta reacción, la sustitución isotópica produce un efecto isotópico cinético inverso, y los autores informan un efecto isotópico cinético tan bajo como 1,74 x 10, que es el efecto de isótopo cinético más pequeño jamás informado.

El efecto isotópico cinético conduce a una distribución específica de los isótopos de deuterio en los productos naturales, dependiendo de la ruta por la que fueron sintetizados en la naturaleza. Por espectroscopia de RMN, es fácil detectar si el alcohol en el vino se fermentó a partir de glucosa o de sacarosa añadida ilícitamente.

Otro mecanismo de reacción que se aclaró utilizando el efecto isotópico cinético es la halogenación del tolueno: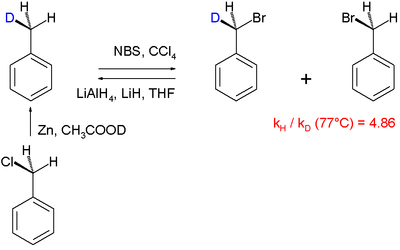

En este estudio particular de "KIE intramolecular", un hidrógeno bencílico sufre una sustitución radical por bromo utilizando N -bromosuccinimida como agente de bromación. Se encontró que PhCH ₃ broma 4.86x más rápido que PhCD ₃. Un KIE grande de 5,56 está asociado con la reacción de cetonas con bromo e hidróxido de sodio.

En esta reacción, el paso limitante de la velocidad es la formación del enolato por desprotonación de la cetona. En este estudio, el KIE se calcula a partir de las constantes de velocidad de reacción de la 2,4-dimetil-3-pentanona regular y su isómero deuterado mediante mediciones de densidad óptica.

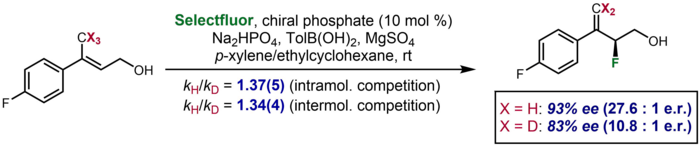
En la catálisis asimétrica, hay casos raros en los que un efecto de isótopo cinético se manifiesta como una diferencia significativa en la enantioselectividad observada para un sustrato deuterado en comparación con uno no deuterado. Toste y colaboradores informaron de un ejemplo, en el que un sustrato deuterado produjo una enantioselectividad del 83 % de ee, en comparación con el 93 % de ee del sustrato no deuterado. El efecto se tomó para corroborar datos adicionales de KIE de competencia intermolecular e intramolecular que sugirieron la escisión del enlace CH/D en el paso de determinación de enantio.