Ecuación de Van der Waals

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ecuación de gas del estado que representa el comportamiento de gas no ideal

En química y termodinámica, la ecuación de Van der Waals (o ecuación de estado de Van der Waals) es una ecuación de estado que amplía la ley de los gases ideales para incluir la efectos de la interacción entre las moléculas de un gas, así como la explicación del tamaño finito de las moléculas.

La ley de los gases ideales trata a las moléculas de gas como partículas puntuales que interactúan con sus contenedores pero no entre sí, lo que significa que ni ocupan espacio ni cambian la energía cinética durante las colisiones (es decir, todas las colisiones son perfectamente elásticas). La ley de los gases ideales establece que el volumen V ocupado por n moles de cualquier gas tiene una presión P a la temperatura T dada por la siguiente relación, donde R es la constante de los gases:

PV=nRT

Para contabilizar el volumen ocupado por moléculas de gas real, la ecuación de Van der Waals reemplaza $V/n$ en la ley de gas ideal ${displaystyle (V_{m}-b)}$ , donde V_m es el volumen molar del gas y b es el volumen ocupado por las moléculas de un mole:

{displaystyle P(V_{m}-b)=RT}

Van der Waals ecuación en una pared en Leiden

La segunda modificación hecha a la ley de gas ideal representa la interacción entre moléculas del gas. La ecuación Van der Waals incluye interacción intermolecular añadiendo a la presión observada P en la ecuación del estado un término de la forma ${displaystyle a/V_{m}^{2}}$ , donde a es una constante cuyo valor depende del gas.

La ecuación completa de Van der Waals es por lo tanto:

{displaystyle left(P+a{frac {1}{V_{m}^{2}}}right)(V_{m}-b)=RT}

Para n moles de gas, también se puede escribir como:

{displaystyle left(P+a{frac {n^{2}}{V^{2}}}right)(V-nb)=nRT}

Cuando el volumen molar V_m es grande, b se vuelve insignificante en comparación con V_m, a/V_m² se vuelve insignificante con respecto a P, y el Van der La ecuación de Waals se reduce a la ley de los gases ideales, PV_m=RT.

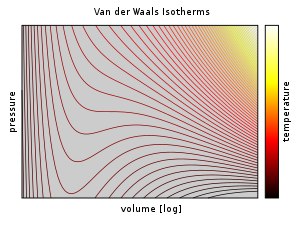
Esta ecuación se aproxima al comportamiento de los fluidos reales por encima de sus temperaturas críticas y es cualitativamente razonable para sus estados líquido y gaseoso a baja presión a bajas temperaturas. Sin embargo, cerca de las transiciones de fase entre gas y líquido, en el rango de p, V y T donde la fase líquida y la fase gaseosa están en equilibrio, la ecuación de Van der Waals no logra modelar con precisión el comportamiento experimental observado. En particular, p es una función constante de V a temperaturas dadas en estas regiones. Como tal, el modelo de Van der Waals no es útil para cálculos destinados a predecir el comportamiento real en regiones cercanas a puntos críticos. Las correcciones para abordar estas deficiencias predictivas incluyen la regla de áreas iguales y el principio de los estados correspondientes.

La ecuación lleva el nombre de su desarrollador, el físico holandés Johannes Diderik van der Waals.

Resumen e historial

La ecuación de Van der Waals es una ecuación de estado termodinámica basada en la teoría de que los fluidos están compuestos de partículas con volúmenes distintos de cero y sujetos a una fuerza de atracción entre partículas (no necesariamente por pares). Se basó en el trabajo de química física teórica realizado a fines del siglo XIX por Johannes Diderik van der Waals, quien realizó un trabajo relacionado con la fuerza de atracción que también lleva su nombre. Se sabe que la ecuación se basa en un conjunto tradicional de derivaciones derivadas de Van der Waals' y esfuerzos relacionados, así como un conjunto de derivaciones basadas en termodinámica estadística, ver más abajo.

Van der Waals' los primeros intereses estaban principalmente en el campo de la termodinámica, donde una primera influencia fue el trabajo publicado de Rudolf Clausius sobre el calor en 1857; otras influencias significativas fueron los escritos de James Clerk Maxwell, Ludwig Boltzmann y Willard Gibbs. Después de la búsqueda inicial de credenciales de enseñanza, Van der Waals' Los cursos de pregrado en matemáticas y física en la Universidad de Leiden en los Países Bajos lo llevaron (con obstáculos significativos) a su aceptación para realizar estudios de doctorado en Leiden con Pieter Rijke. Si bien su disertación ayuda a explicar la observación experimental en 1869 por parte del profesor irlandés de química Thomas Andrews (Queen's University Belfast) de la existencia de un punto crítico en los fluidos, el historiador de la ciencia Martin J. Klein afirma que no está claro si Van der Waals estaba al tanto de Andrews' resultados cuando comenzó su trabajo de doctorado.

Van der Waals' La investigación doctoral culminó en una disertación de 1873 que proporcionó una teoría semicuantitativa que describe el cambio de estado gas-líquido y el origen de una temperatura crítica, Over de Continuïteit van den Gas- en Vloeistoftoestand (holandés; en Inglés, Sobre la continuidad del estado gaseoso y líquido). Fue en esta disertación que aparecieron las primeras derivaciones de lo que ahora llamamos la ecuación de Van der Waals. James Clerk Maxwell revisó y elogió su contenido publicado en la revista científica británica Nature, y Van der Waals inició un trabajo independiente que resultaría en su recepción del Premio Nobel en 1910, que enfatizaba la contribución de su formulación. de esta "ecuación de estado para gases y líquidos".

Ecuación

Van der Waals esotherms. El modelo predice correctamente una fase líquida casi incompresible, pero las oscilaciones en la zona de transición de fase no encajan en los datos experimentales.

Van der Waals estromas y oscilaciones, temperaturas, T, por debajo y por encima T_C. Se muestra en esto PV diagrama son una serie de 5 isotérmos para temperaturas que van desde abajo (azul) hasta arriba (rojo) T_C (la temperatura crítica), donde la subida y el descenso hacia abajo en el isotomo predicho por la ecuación de Van der Waals (la "oscilación", especialmente evidente para los dos isotemos para los valores de T. T_C) es evidente en la región de la transición de fase gas-liquid.

La ecuación relaciona cuatro variables de estado: la presión del fluido p, el volumen total del contenedor del fluido V, el número de partículas N, y la temperatura absoluta del sistema T.

La forma microscópica intensiva de la ecuación es:

{displaystyle left(p+{frac {a'}{v^{2}}}right)left(v-b'right)=k_{text{B}}T}

dónde

v=V/N

es el volumen del recipiente ocupado por cada partícula (no la velocidad de una partícula), y k_B es la constante de Boltzmann. Introduce dos nuevos parámetros: a′, una medida de la atracción promedio entre partículas, y b′, el volumen excluido de v por uno partícula.

La ecuación también se puede escribir en forma molar extensiva:

left(p+{frac {n^{2}a}{V^{2}}}right)left(V-nbright)=nRT

o también:

{displaystyle p={frac {RT}{V_{m}-b}}-{frac {a}{V_{m}^{2}}}}

dónde

a=N_{A}^{2}a'

es una medida de la atracción promedio entre partículas,

{displaystyle b=N_{text{A}}b'}

es el volumen excluido por un mol de partículas,

{displaystyle n=N/N_{text{A}}}

es el número de moles,

{displaystyle R=N_{text{A}}k_{text{B}}}

es la constante universal de los gases, k_B es la constante de Boltzmann y N_A es la de Avogadro constante,

{displaystyle V_{m}={frac {V}{n}}=vN_{A}}

es el volumen molar específico.

También la constante a, b se puede expresar en términos de las constantes críticas:

{displaystyle a={frac {27}{64}}{frac {R^{2}T_{c}^{2}}{P_{c}}}}

{displaystyle b={frac {1}{8}}{frac {RT_{c}}{P_{c}}}}

Y las constantes críticas se pueden expresar en términos de a, b:

{displaystyle P_{c}={frac {a}{27b^{2}}}}

{displaystyle T_{c}={frac {8a}{27bR}}}

{displaystyle V_{m,c}=3b}

Debe hacerse una distinción cuidadosa entre el volumen disponible para una partícula y el volumen de una partícula. En la ecuación intensiva, v es igual al espacio total disponible para cada partícula, mientras que el parámetro b′ es proporcional al volumen propio de una sola partícula: el volumen limitado por el radio atómico. Esto se resta de v debido al espacio que ocupa una partícula. En Van der Waals' derivación original, dada a continuación, b' es cuatro veces el volumen propio de la partícula. Observe además que la presión p tiende a infinito cuando el recipiente está completamente lleno de partículas, de modo que no queda espacio vacío para que las partículas se muevan; esto ocurre cuando V = nb.

Mezcla de gases

Si una mezcla de $n$ se están considerando los gases, y cada gas tiene su propio $a$ (atracción entre moléculas) y $b$ (volumen ocupado por moléculas) valores, entonces $a$ y $b$ para la mezcla se puede calcular como

m

= número total de lunares de gas presentes,

para cada uno

i

m_{i}

= número de lunares de gas

i

presentes, y

{displaystyle x_{i}={frac {m_{i}}{m}}}

{displaystyle a=sum _{i=1}^{i=n}sum _{j=1}^{i=n}(x_{i}x_{j}{sqrt {a_{i}a_{j}}})}

{displaystyle b=sum _{i=1}^{i=n}sum _{j=1}^{i=n}(x_{i}x_{j}{sqrt {b_{i}b_{j}}})}

y la regla de añadir presiones parciales se invalida si el resultado numérico de la ecuación ${displaystyle left(p+({n^{2}a}/{V^{2}})right)left(V-nbright)=nRT}$ es significativamente diferente de la ecuación de gas ideal $pV=nRT$ .

Forma reducida

La ecuación de Van der Waals también se puede expresar en términos de propiedades reducidas:

{displaystyle left(P_{r}+{frac {3}{V_{r}^{2}}}right)left(V_{r}-{frac {1}{3}}right)={frac {8}{3}}T_{r}}

La ecuación en forma reducida es exactamente la misma para todos los gases, esto es consistente con el Teorema de estados correspondientes.

Esto produce un factor de compresibilidad crítico de 3/8. Razones para la modificación de la ecuación del gas ideal: El estado de la ecuación para el gas ideal es PV=RT. En la derivación de las leyes de los gases ideales sobre la base de la teoría cinética de los gases, se han hecho algunas suposiciones.

Factor de compresibilidad

El factor de compresibilidad para la ecuación de Van der Waals es:

{displaystyle Z={frac {PV_{m}}{RT}}={frac {V_{m}}{V_{m}-b}}-{frac {a}{V_{m}RT}}}

O en forma reducida por sustitución ${displaystyle P_{r}=P/P_{c},T_{r}=T/T_{c},V_{r}=V_{m}/V_{c}}$ :

{displaystyle Z={frac {V_{r}}{V_{r}-{frac {1}{3}}}}-{frac {9}{8V_{r}T_{r}}}}

En el punto crítico:

{displaystyle Z_{c}={frac {P_{c}V_{c}}{RT_{c}}}={frac {3}{8}}=0.375}

Validez

La ecuación de Van der Waals es matemáticamente simple, pero sin embargo predice la transición observada experimentalmente entre vapor y líquido, y predice el comportamiento crítico. También predice y explica adecuadamente el efecto Joule-Thomson (cambio de temperatura durante la expansión adiabática), que no es posible en el gas ideal.

Por encima de la temperatura crítica, T_C, la ecuación de Van der Waals es una mejora sobre la ley de los gases ideales, y para temperaturas más bajas, es decir, T < T_C, la ecuación también es cualitativamente razonable para los estados líquido y gaseoso a baja presión; sin embargo, con respecto a la transición de fase de primer orden, es decir, el rango de (p, V, T) donde una fase líquida y una fase gaseosa estarían en equilibrio, la ecuación parece fallar. predecir el comportamiento experimental observado, en el sentido de que normalmente se observa que p es constante en función de V para una temperatura dada en la región de dos fases. Esta aparente discrepancia se resuelve en el contexto del equilibrio líquido-vapor: a una temperatura particular, existen dos puntos en la isoterma de Van der Waals que tienen el mismo potencial químico y, por lo tanto, un sistema en equilibrio termodinámico parecerá atravesar una línea recta. en el diagrama p–V a medida que cambia la proporción de vapor a líquido. Sin embargo, en tal sistema, en realidad solo hay dos puntos presentes (el líquido y el vapor) en lugar de una serie de estados conectados por una línea, por lo que conectar el lugar geométrico de los puntos es incorrecto: no es una ecuación de múltiples estados, sino una ecuación de (un solo) estado. De hecho, es posible comprimir un gas más allá del punto en el que normalmente se condensaría, dadas las condiciones adecuadas, y también es posible expandir un líquido más allá del punto en el que normalmente herviría. Tales estados se denominan "metaestables" estados Tal comportamiento es cualitativamente (aunque quizás no cuantitativamente) predicho por la ecuación de estado de Van der Waals.

Sin embargo, los valores de las cantidades físicas predichas con la ecuación de estado de Van der Waals "concuerdan muy poco con el experimento", por lo que la utilidad del modelo se limita a aspectos cualitativos en lugar de cuantitativos. propósitos Las correcciones de base empírica se pueden insertar fácilmente en el modelo de Van der Waals (consulte la corrección de Maxwell, a continuación), pero al hacerlo, la expresión modificada ya no es un modelo analítico tan simple; en este sentido, otros modelos, como los basados en el principio de estados correspondientes, logran un mejor ajuste con aproximadamente el mismo trabajo. Incluso con sus deficiencias reconocidas, el uso generalizado de la ecuación de Van der Waals en los libros de texto universitarios estándar de química física deja en claro su importancia como herramienta pedagógica para ayudar a comprender las ideas fundamentales de la química física involucradas en el desarrollo de teorías de vapor. Comportamiento de líquidos y ecuaciones de estado. Además, otras ecuaciones de estado (más precisas), como la ecuación de estado de Redlich-Kwong y Peng-Robinson, son esencialmente modificaciones de la ecuación de estado de Van der Waals.

Derivación

Los libros de texto de química física generalmente dan dos derivaciones de la ecuación del título. Una es la derivación convencional que se remonta a Van der Waals, una ecuación mecánica de estado que no puede usarse para especificar todas las funciones termodinámicas; la otra es una derivación de mecánica estadística que hace explícito el potencial intermolecular despreciado en la primera derivación. Una ventaja particular de la derivación mecánica estadística es que produce la función de partición para el sistema y permite especificar todas las funciones termodinámicas (incluida la ecuación de estado mecánica).

Derivación convencional

Considere un mol de gas compuesto de partículas puntuales que no interactúan y que satisfacen la ley de los gases ideales: (consulte cualquier texto estándar de química física, op. cit.)

p = frac{RT}{V_mathrm{m}}.

A continuación, suponga que todas las partículas son esferas duras del mismo radio finito r (el radio de Van der Waals). El efecto del volumen finito de las partículas es disminuir el espacio vacío disponible en el que las partículas pueden moverse libremente. Debemos reemplazar V por V − b, donde b se llama el volumen excluido (por mol) o "co-volumen". La ecuación corregida se convierte en

p={frac {RT}{V_{mathrm {m} }-b}}.

El volumen excluido $b$ no es sólo igual al volumen ocupado por las partículas sólidas de tamaño finito, sino que en realidad cuatro veces el volumen molecular total para un topo de un gas Van der waals. Para ver esto, debemos darnos cuenta de que una partícula está rodeada de una esfera de radio 2r (dos veces el radio original) que está prohibido para los centros de las otras partículas. Si la distancia entre dos centros de partículas fuera menor que 2r, significaría que las dos partículas se penetran entre sí, que, por definición, las esferas duras no pueden hacer.

El volumen excluido para las dos partículas (de diámetro promedio d o radio r) es

b'_{2}=4pi d^{3}/3=8times (4pi r^{3}/3)

que, dividido por dos (el número de partículas que chocan), da el volumen excluido por partícula:

b'=b'_{2}/2quad rightarrow quad b'=4times (4pi r^{3}/3)

Entonces b′ es cuatro veces el volumen propio de la partícula. Fue un punto de preocupación para Van der Waals que el factor cuatro produce un límite superior; los valores empíricos para b′ suelen ser más bajos. Por supuesto, las moléculas no son infinitamente duras, como pensaba Van der Waals, y suelen ser bastante blandas. Para obtener el volumen excluido por mol solo necesitamos multiplicar por el número de moléculas en un mol, es decir, por el número de avogadro:

b=N_{A}b'

A continuación, introducimos una fuerza de atracción (no necesariamente por pares) entre las partículas. Van der Waals supuso que, a pesar de la existencia de esta fuerza, la densidad del fluido es homogénea; además, supuso que el rango de la fuerza de atracción es tan pequeño que la gran mayoría de las partículas no sienten que el recipiente es de tamaño finito. Dada la homogeneidad del fluido, la mayor parte de las partículas no experimentan una fuerza neta que las tire hacia la derecha o hacia la izquierda. Esto es diferente para las partículas en las capas superficiales directamente adyacentes a las paredes. Sienten una fuerza neta de las partículas a granel que las empujan hacia el contenedor, porque esta fuerza no es compensada por partículas en el lado donde está la pared (otra suposición aquí es que no hay interacción entre las paredes y las partículas, lo cual no es cierto, como se puede ver en el fenómeno de la formación de gotas; la mayoría de los tipos de líquido muestran adherencia). Esta fuerza neta disminuye la fuerza ejercida sobre la pared por las partículas en la capa superficial. La fuerza neta sobre una partícula de la superficie, tirando de ella hacia el contenedor, es proporcional a la densidad numérica. Al considerar un mol de gas, el número de partículas será N_A

C=N_{mathrm {A} }/V_{mathrm {m} }

El número de partículas en las capas superficiales es, de nuevo suponiendo homogeneidad, también proporcional a la densidad. En total, la fuerza sobre las paredes disminuye en un factor proporcional al cuadrado de la densidad, y la presión (fuerza por unidad de superficie) disminuye en

{displaystyle a'C^{2}=a'left({frac {N_{mathrm {A} }}{V_{mathrm {m} }}}right)^{2}={frac {a}{V_{mathrm {m} }^{2}}}}

para que

p={frac {RT}{V_{mathrm {m} }-b}}-{frac {a}{V_{mathrm {m} }^{2}}}Rightarrow left(p+{frac {a}{V_{mathrm {m} }^{2}}}right)(V_{mathrm {m} }-b)=RT.

Al escribir n para el número de moles y nV_m = V, la ecuación obtiene el segundo forma dada arriba,

left(p+{frac {n^{2}a}{V^{2}}}right)(V-nb)=nRT.

Es de cierto interés histórico señalar que Van der Waals, en su discurso de premio Nobel, dio crédito a Laplace por el argumento de que la presión se reduce proporcionalmente al cuadrado de la densidad.

Derivación termodinámica estadística

La función de partición canónica Z de un gas ideal que consta de N = nN_A idénticos (que no interactúan) partículas, es:

{displaystyle Z={frac {z^{N}}{N!}}quad {hbox{with}}quad z={frac {V}{Lambda ^{3}}}}

Donde $Lambda$ es la longitud de onda térmica de Broglie,

Lambda ={sqrt {frac {h^{2}}{2pi mkT}}}

con las definiciones habituales: h es la constante de Planck, m la masa de una partícula, k la constante de Boltzmann y T la temperatura absoluta. En un gas ideal z es la función de partición de una sola partícula en un recipiente de volumen V. Para derivar la ecuación de Van der Waals asumimos ahora que cada partícula se mueve independientemente en un campo potencial promedio ofrecido por las otras partículas. El promedio de las partículas es fácil porque supondremos que la densidad de partículas del fluido de Van der Waals es homogénea. La interacción entre un par de partículas, que son esferas duras, se toma como

<math alttext="{displaystyle u(r)={begin{cases}infty &{hbox{when}}quad ru()r)={}JUEGO JUEGO cuandor.d,− − ε ε ()dr)6cuandor≥ ≥ d,{displaystyle u(r)={begin{cases}infty &hbox{ when}quad r maded,\\-epsilon left({frac {d}right)}{6} {hbox{cuando}quad rgeq d,end{cases}}}}}<img alt="u(r)={begin{cases}infty &{hbox{when}}quad r

r es la distancia entre los centros de las esferas y d es la distancia donde las esferas duras se tocan (twice el Van der Waals radius). La profundidad del pozo Van der Waals es $epsilon$ .

Debido a que las partículas no están acopladas bajo el campo medio hamiltoniano, la aproximación del campo medio de la función de partición total todavía se factoriza,

{displaystyle Z=z^{N}/N!}

pero el potencial intermolecular requiere dos modificaciones a z. Primero, debido al tamaño finito de las partículas, no todo V está disponible, sino sólo V − Nb', donde (al igual que en la derivación convencional anterior)

b'=2pi d^{3}/3

En segundo lugar, insertamos un factor de Boltzmann exp[ - ϕ/2kT] para cuidar el potencial intermolecular promedio. Dividimos aquí el potencial por dos porque esta energía de interacción se comparte entre dos partículas. De este modo

{displaystyle z={frac {(V-Nb'),e^{-phi /(2kT)}}{Lambda ^{3}}}.}

La atracción total que siente una sola partícula es

phi =int _{d}^{infty }u(r){frac {N}{V}}4pi r^{2}dr,

donde asumimos que en una capa de espesor dr hay N/V 4π r ²dr partículas. Esta es una aproximación de campo medio; se promedia la posición de las partículas. En realidad, la densidad cercana a la partícula es diferente a la lejana, como puede describirse mediante una función de correlación de pares. Además, se desprecia que el fluido está encerrado entre paredes. Realizando la integral obtenemos

phi =-2a'{frac {N}{V}}quad {hbox{with}}quad a'=epsilon {frac {2pi d^{3}}{3}}=epsilon b'.

Por lo tanto, obtenemos,

{displaystyle ln Z=Nln {(V-Nb')}+{frac {N^{2}a'}{VkT}}-Nln {(Lambda ^{3})}-ln {N!}}

De la termodinámica estadística sabemos que

{displaystyle p=kT{frac {partial ln Z}{partial V}}}

para que sólo tengamos que diferenciar los términos que contienen $V$ . Tenemos

p={frac {NkT}{V-Nb'}}-{frac {N^{2}a'}{V^{2}}}Rightarrow left(p+{frac {N^{2}a'}{V^{2}}}right)(V-Nb')=NkTRightarrow left(p+{frac {n^{2}a}{V^{2}}}right)(V-nb)=nRT.

Regla de áreas iguales de Maxwell

Van der Waals oscilación de estero y las áreas iguales de Maxwell. La regla de Maxwell elimina el comportamiento oscilante del isomo en la zona de transición de fase definiéndolo como un cierto isobar en esa zona. El isomo anterior es para una temperatura reducida T_R=0.9. La corrección de Maxwell está a presión de vapor p_VΩ0.64700 entre el volumen reducido del líquido puro V_L■0.60340 y el gas puro V_GΩ2.3488 a la presión de vapor.

Debajo de la temperatura crítica, la ecuación de Van der Waals parece predecir relaciones cualitativamente incorrectas. A diferencia de los gases ideales, los isotérmicos p-V oscilan con un mínimo relativo (d) y un máximo relativo (e). Cualquier presión entre p_d y p_e parece tener 3 valores para el volumen, contradiciendo la observación experimental que dos variables estatales determinan completamente el estado de un sistema único. Además, la compresibilidad isotérmica es negativa entre d y e (equivalentemente) $0}" xmlns="http://www.w3.org/1998/Math/MathML">()∂ ∂ P/∂ ∂ V)T,N■0{displaystyle scriptstyle left({partial P}/{partial V}right)_{T,N} {0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ed8a34679568edc0e2bb6ccfe32e326c328590a9" style="vertical-align: -1.005ex; width:11.223ex; height:2.509ex;"/>$ ), que no puede describir un sistema en equilibrio.

Para abordar estos problemas, James Clerk Maxwell reemplazó la isoterma entre los puntos a y c con una línea horizontal colocada de modo que las áreas de las dos regiones sombreadas fueran iguales (reemplazando la curva a-d-b-e-c) con una línea recta de a a c); esta porción de la isoterma corresponde al equilibrio líquido-vapor. Las regiones de la isoterma de a–d y de c–e se interpretan como estados metaestables de super- líquido calentado y vapor sobreenfriado, respectivamente. La regla de áreas iguales se puede expresar como:

{displaystyle p_{V}(V_{G}-V_{L})=int _{V_{L}}^{V_{G}}p,dV}

donde p_V es la presión de vapor (parte plana de la curva), V_L es la volumen de la fase líquida pura en el punto a del diagrama, y V_G es el volumen de la fase gaseosa pura en el punto c en el diagrama. Una mezcla de dos fases a p_V ocupará un volumen total entre V_L y V_G, según lo determinado por la regla de la palanca de Maxwell.

Maxwell justificó la regla basándose en el hecho de que el área en un diagrama pV corresponde al trabajo mecánico, diciendo que el trabajo realizado en el sistema va de c a b debe ser igual al trabajo liberado al pasar de a a b. Esto se debe a que el cambio en la energía libre A(T,V) es igual al trabajo realizado durante un proceso reversible y, como variable de estado, la energía libre debe ser independiente de la trayectoria. En particular, el valor de A en el punto b debe ser el mismo independientemente de si el camino tomado es de izquierda o derecha a través de la isobara horizontal, o si sigue la ruta original de Van der. Isoterma de Waals.

Esta derivación no es del todo rigurosa, ya que requiere un camino reversible a través de una región de inestabilidad termodinámica, mientras que b es inestable. Sin embargo, las derivaciones modernas del potencial químico llegan a la misma conclusión, y sigue siendo una modificación necesaria a la de Van der Waals ya cualquier otra ecuación de estado analítica.

De potencial químico

La regla de áreas iguales de Maxwell también se puede derivar de la suposición de un potencial químico igual μ de las fases líquida y vapor coexistentes. En la isoterma que se muestra en el gráfico anterior, los puntos a y c son el único par de puntos que cumplen la condición de equilibrio de tener la misma presión, temperatura y potencial químico. De ello se deduce que los sistemas con volúmenes intermedios entre estos dos puntos consistirán en una mezcla de líquido puro y gas con volúmenes específicos iguales a las fases de líquido puro y gas en los puntos a y c.

La ecuación de Van der Waals se puede resolver para V_G y V_L como funciones de la temperatura y la presión de vapor p_V. Desde:

{displaystyle p=-left({frac {partial A}{partial V}}right)_{T,N}}

donde A es la energía libre de Helmholtz, se deduce que la regla de áreas iguales se puede expresar como:

{displaystyle p_{V}={frac {A(V_{L},T,N)-A(V_{G},T,N)}{V_{G}-V_{L}}}}

Dado que los volúmenes de gas y líquido son funciones de p_V y T únicamente, esta ecuación se resuelve numéricamente para obtener p_V en función de la temperatura (y el número de partículas N), que luego se pueden usar para determinar los volúmenes de gas y líquido.

Locus de coexistencia para dos fases del fluido Van der Waals

Se muestra un gráfico pseudo-3D del lugar geométrico de los volúmenes de líquido y vapor frente a la temperatura y la presión en la figura adjunta. Se ve que los dos lugares se encuentran en el punto crítico (1,1,1) sin problemas. También se muestra una isoterma del fluido de Van der Waals tomada en T _r = 0,90 donde las intersecciones de la isoterma con los loci ilustran el requisito del constructo de que el dos áreas (roja y azul, que se muestran) son iguales.

Otros parámetros, formularios y aplicaciones

Otros parámetros termodinámicos

Reiteramos que el volumen extensivo V está relacionado con el volumen por partícula v=V/N donde N = nN_A es el número de partículas en el sistema. La ecuación de estado no nos da todos los parámetros termodinámicos del sistema. Podemos tomar la ecuación para la energía de Helmholtz A

A=-kTln Q.,

De la ecuación derivada arriba para lnQ, encontramos

A(T,V,N)=-NkTleft[1+ln left({frac {(V-Nb')T^{3/2}}{NPhi }}right)right]-{frac {a'N^{2}}{V}}.

Donde Φ es una constante indeterminada, que puede tomarse de la ecuación de Sackur-Tetrode para un gas ideal como:

Phi =T^{3/2}Lambda ^{3}=left({frac {h}{sqrt {2pi mk}}}right)^{3}

Esta ecuación expresa A en términos de sus variables naturales V y T y, por lo tanto, nos brinda toda la información termodinámica sobre el sistema. La ecuación mecánica de estado ya se derivó anteriormente

{displaystyle p=-left({frac {partial A}{partial V}}right)_{N,T}={frac {NkT}{V-Nb'}}-{frac {a'N^{2}}{V^{2}}}.}

La ecuación de estado de entropía produce la entropía (S)

{displaystyle S=-left({frac {partial A}{partial T}}right)_{N,V}=Nkleft[ln left({frac {(V-Nb')T^{3/2}}{NPhi }}right)+{frac {5}{2}}right]}

a partir de la cual podemos calcular la energía interna

U=A+TS={frac {3}{2}},NkT-{frac {a'N^{2}}{V}}.

Se pueden escribir ecuaciones similares para el otro potencial termodinámico y el potencial químico, pero expresar cualquier potencial en función de la presión p requerirá la solución de un polinomio de tercer orden, lo que produce un complicado expresión. Por tanto, expresar la entalpía y la energía de Gibbs como funciones de sus variables naturales será complicado.

Forma reducida

Aunque la constante material a y b en la forma habitual de la ecuación de Van der Waals difiere para cada fluido considerado, la ecuación se puede reformular en una forma invariable aplicable a todos los fluidos.

Definiendo las siguientes variables reducidas (f_R, f_C son las versiones de variables reducidas y críticas de f, respectivamente),

p_{R}={frac {p}{p_{C}}},qquad v_{R}={frac {v}{v_{C}}},quad {hbox{and}}quad T_{R}={frac {T}{T_{C}}}

dónde

p_C=frac{a'}{27b'^2}, qquad displaystyle{v_C=3b'},quadhbox{and}quad kT_C=frac{8a'}{27b'}

como lo muestra Salzman.

La primera forma de la ecuación de estado de Van der Waals dada anteriormente puede reformularse en la siguiente forma reducida:

{displaystyle left(p_{R}+{frac {3}{v_{R}^{2}}}right)(3v_{R}-1)=(8T_{R}}

)

Esta ecuación es invariante para todos los fluidos; es decir, se aplica la misma ecuación de estado en forma reducida, sin importar cuáles sean a y b para el fluido en particular.

Esta invariancia también puede entenderse en términos del principio de los estados correspondientes. Si dos fluidos tienen la misma presión reducida, volumen reducido y temperatura reducida, decimos que sus estados son correspondientes. Los estados de dos fluidos pueden ser correspondientes incluso si su presión, volumen y temperatura medidos son muy diferentes. Si los dos fluidos' los estados son correspondientes, existen en el mismo régimen de la ecuación de estado en forma reducida. Por lo tanto, responderán a los cambios más o menos de la misma manera, aunque sus características físicas medibles puedan diferir significativamente.

Ecuación cúbica

La ecuación de Van der Waals es una ecuación de estado cúbica; en la formulación reducida la ecuación cúbica es:

{v_{R}^{3}}-{frac {1}{3}}left({1+{frac {8T_{R}}{p_{R}}}}right){v_{R}^{2}}+{frac {3}{p_{R}}}v_{R}-{frac {1}{p_{R}}}=0

A temperatura crítica, donde $T_{R}=p_{R}=1$ conseguimos lo esperado

{displaystyle {v_{R}^{3}}-3v_{R}^{2}+3v_{R}-1=left(v_{R}-1right)^{3}=0quad Longleftrightarrow quad v_{R}=1}

Para T_R < 1, hay 3 valores para v_R. Para T_R > 1, hay 1 valor real para v_R.

La solución de esta ecuación para el caso en que hay tres raíces separadas se puede encontrar en la construcción de Maxwell.

Aplicación a fluidos compresibles

La ecuación también se puede utilizar como ecuación PVT para fluidos comprimibles (por ejemplo, polímeros). En este caso, los cambios de volumen específicos son pequeños y se pueden escribir de forma simplificada:

(p+A)(V-B)=CT,,

donde p es la presión, V es el volumen específico, T es la temperatura y A, B, C son parámetros.

Contenido relacionado

Más resultados...