Ecuación de Taft

La ecuación de Taft es una relación lineal de energía libre (LFER) utilizada en química orgánica física en el estudio de mecanismos de reacción y en el desarrollo de relaciones cuantitativas estructura-actividad para compuestos orgánicos. Fue desarrollado por Robert W. Taft en 1952 como una modificación a la ecuación de Hammett. Mientras que la ecuación de Hammett explica cómo los efectos de campo, inductivos y de resonancia influyen en las velocidades de reacción, la ecuación de Taft también describe los efectos estéricos de un sustituyente. La ecuación de Taft se escribe como:

donde es la relación de la velocidad de la reacción sustituida en comparación con la reacción de referencia, ρ* es el factor de sensibilidad de la reacción a los efectos polares, σ* es la constante del sustituyente polar que describe el campo y los efectos inductivos del sustituyente, δ es el factor de sensibilidad para la reacción a los efectos estéricos, y E _s es la constante del sustituyente estérico.

Constantes de sustituyentes polares, σ*

Las constantes de sustituyentes polares describen la forma en que un sustituyente influirá en una reacción a través de efectos polares (inductivos, de campo y de resonancia). Para determinar σ Taft estudió la hidrólisis de ésteres metílicos (RCOOMe). El uso de tasas de hidrólisis de ésteres para estudiar los efectos polares fue sugerido por primera vez por Ingold en 1930. La hidrólisis de ésteres puede ocurrir a través de mecanismos catalizados por ácidos y bases, los cuales proceden a través de un intermedio tetraédrico. En el mecanismo catalizado por una base, el reactivo pasa de una especie neutra a un intermedio cargado negativamente en el paso (lento) determinante de la velocidad, mientras que en el mecanismo catalizado por un ácido, un reactivo cargado positivamente pasa a un intermedio cargado positivamente.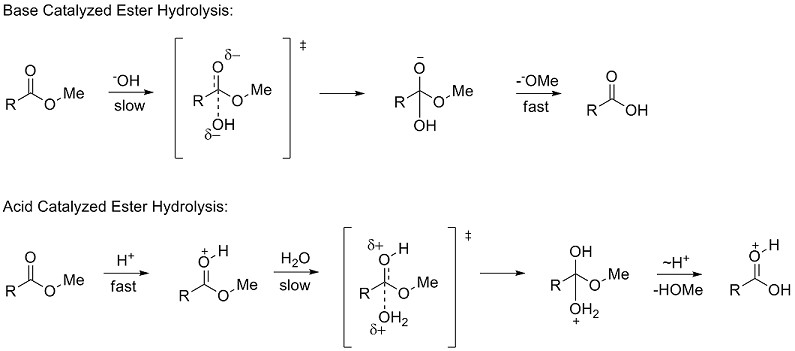

Debido a los intermedios tetraédricos similares, Taft propuso que, en condiciones idénticas, cualquier factor estérico debería ser casi el mismo para los dos mecanismos y, por lo tanto, no influiría en la relación de las tasas. Sin embargo, debido a la diferencia en la acumulación de carga en los pasos de determinación de la velocidad, se propuso que los efectos polares solo influirían en la velocidad de reacción de la reacción catalizada por la base, ya que se formaba una nueva carga. Definió la constante del sustituyente polar σ* como:

donde log(ks _/ k _{CH 3}) _B es la relación de la velocidad de la reacción catalizada por base en comparación con la reacción de referencia, log(ks _/ k _{CH 3}) _A es la relación de la velocidad de la reacción catalizada por ácido en comparación con la reacción de referencia, y ρ* es una constante de reacción que describe la sensibilidad de la serie de reacciones. Para la serie de reacciones de definición, ρ* se estableció en 1 y R = metilo se definió como la reacción de referencia (σ* = cero). El factor de 1/2,48 se incluye para hacer que σ* sea similar en magnitud a los valores de σ de Hammett.

Constantes de sustituyentes estéricos, E _s

Aunque la hidrólisis de ésteres catalizada por ácido y catalizada por base da estados de transición para los pasos determinantes de la velocidad que tienen diferentes densidades de carga, sus estructuras difieren solo en dos átomos de hidrógeno. Por tanto, Taft asumió que los efectos estéricos influirían por igual en ambos mecanismos de reacción. Debido a esto, la constante del sustituyente estérico E _s se determinó únicamente a partir de la reacción catalizada por ácido, ya que esto no incluiría efectos polares. E _s se definió como:

donde k _s es la velocidad de la reacción estudiada y es la velocidad de la reacción de referencia (R = metilo). δ es una constante de reacción que describe la susceptibilidad de una serie de reacciones a los efectos estéricos. Para la definición, la serie de reacciones δ se fijó en 1 y E _s para la reacción de referencia se fijó en cero. Esta ecuación se combina con la ecuación de σ* para dar la ecuación de Taft completa.

Al comparar los valores de E _s para metilo, etilo, isopropilo y terc-butilo, se ve que el valor aumenta al aumentar el volumen estérico. Sin embargo, debido a que el contexto tendrá un efecto sobre las interacciones estéricas, algunos valores de E _s pueden ser mayores o menores de lo esperado. Por ejemplo, el valor del fenilo es mucho mayor que el del terc - butilo. Cuando se comparan estos grupos usando otra medida de volumen estérico, valores de tensión axial, el grupo terc -butilo es más grande.

Otros parámetros estéricos para LFER

Además del parámetro estérico E _s de Taft, se han definido otros parámetros estéricos que son independientes de los datos cinéticos. Charton ha definido valores v que se derivan de los radios de van der Waals. Usando mecánica molecular, Meyers ha definido valores de V que se derivan del volumen de la porción del sustituyente que está dentro de los 0,3 nm del centro de reacción.

Factores de sensibilidad

Factor de sensibilidad polar, ρ*

Similar a los valores ρ para los gráficos de Hammett, el factor de sensibilidad polar ρ* para los gráficos de Taft describirá la susceptibilidad de una serie de reacciones a los efectos polares. Cuando los efectos estéricos de los sustituyentes no influyen significativamente en la velocidad de reacción, la ecuación de Taft se simplifica a una forma de la ecuación de Hammett:

El factor de sensibilidad polar ρ* puede obtenerse trazando la relación de las velocidades de reacción medidas (k _s) en comparación con la reacción de referencia () frente a los valores σ* para los sustituyentes. Esta gráfica dará una línea recta con una pendiente igual a ρ*. Similar al valor de Hammett ρ:

• Si ρ* > 1, la reacción acumula carga negativa en el estado de transición y es acelerada por grupos atractores de electrones.
• Si 1 > ρ* > 0, se acumula carga negativa y la reacción es levemente sensible a los efectos polares.
• Si ρ* = 0, la reacción no está influenciada por efectos polares.
• Si 0 > ρ* > −1, se acumula carga positiva y la reacción es levemente sensible a los efectos polares.
• Si −1 > ρ*, la reacción acumula carga positiva y es acelerada por grupos donantes de electrones.

Factor de sensibilidad estérico, δ

Similar al factor de sensibilidad polar, el factor de sensibilidad estérico δ para una nueva serie de reacciones describirá en qué magnitud la velocidad de reacción está influenciada por los efectos estéricos. Cuando una serie de reacciones no está significativamente influenciada por los efectos polares, la ecuación de Taft se reduce a:

Una gráfica de la relación de las tasas versus el valor de E _s para el sustituyente dará una línea recta con una pendiente igual a δ. De manera similar al valor de Hammett ρ, la magnitud de δ reflejará hasta qué punto una reacción está influenciada por efectos estéricos:

• Una pendiente muy pronunciada corresponderá a una alta sensibilidad estérica, mientras que una pendiente poco pronunciada corresponderá a poca o ninguna sensibilidad.

Dado que los valores de E _s son grandes y negativos para los sustituyentes más voluminosos, se sigue que:

• Si δ es positivo, el aumento del volumen estérico disminuye la velocidad de reacción y los efectos estéricos son mayores en el estado de transición.
• Si δ es negativo, el aumento del volumen estérico aumenta la velocidad de reacción y los efectos estéricos se reducen en el estado de transición.

Reacciones influenciadas por efectos polares y estéricos

Cuando tanto los efectos estéricos como los polares influyen en la velocidad de reacción, la ecuación de Taft se puede resolver tanto para ρ* como para δ mediante el uso de métodos estándar de mínimos cuadrados para determinar un plano de regresión bivariante. Taft describió la aplicación de este método para resolver la ecuación de Taft en un artículo de 1957.

Diagramas de Taft en QSAR

La ecuación de Taft se emplea a menudo en química biológica y química médica para el desarrollo de relaciones cuantitativas estructura-actividad (QSAR). En un ejemplo reciente, Sandri y colaboradoreshan utilizado diagramas de Taft en estudios de efectos polares en la aminolisis de β-lactámicos. Han analizado la unión de β-lactámicos a un polímero de poli(etilenimina), que funciona como un simple imitador de la albúmina sérica humana (HSA). Se cree que la formación de un enlace covalente entre las penicilinas y la HSA como resultado de la aminólisis con residuos de lisina está implicada en las alergias a la penicilina. Como parte de sus estudios mecánicos, Sandri y colaboradores trazaron la tasa de aminólisis frente a los valores σ* calculados para 6 penicilinas y no encontraron correlación, lo que sugiere que la tasa está influenciada por otros efectos además de los efectos polares y estéricos.