Ecuación de Nernst

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Derecho físico en electroquímica

En electroquímica, la ecuación de Nernst es una relación termodinámica química que permite calcular el potencial de reducción de una reacción (reacción de media celda o de celda completa) a partir del potencial de electrodo estándar, la temperatura absoluta, el número de electrones involucrados en la reacción redox y las actividades (a menudo aproximadas por concentraciones) de las especies químicas que experimentan reducción y oxidación respectivamente. Lleva el nombre de Walther Nernst, un químico físico alemán que formuló la ecuación.

Expresión

Forma general con actividades químicas

Cuando un oxidante ( $Ox$ ) acepta un número z de electrones ( e⁻) para convertirse en su forma reducida ( $Red$ ), la semirreacción se expresa como:

Ox

+ z e⁻ →

Rojo

El cociente de reacción ( $Q r$ ), también llamado producto de actividad iónica (IAP), es la relación entre las actividades químicas (a) de la forma reducida (el reductor, $a Red$ ) y la forma oxidada (el oxidante, $a Ox$ ). La actividad química de una especie disuelta corresponde a su verdadera concentración termodinámica teniendo en cuenta las interacciones eléctricas entre todos los iones presentes en solución a concentraciones elevadas. Para una especie disuelta determinada, su actividad química (a) es el producto de su coeficiente de actividad (γ) por su concentración molar (mol/L de solución) o molal (mol/kg de agua) (C): a = γ C Por lo tanto, si la concentración (C, también indicada a continuación con corchetes [ ]) de todas las especies disueltas de interés es lo suficientemente baja y sus coeficientes de actividad están cerca de la unidad, sus actividades químicas pueden aproximarse por sus concentraciones como se hace comúnmente al simplificar o idealizar una reacción con fines didácticos:

{displaystyle Q_{r}={frac {a_{text{Red}}}{a_{text{Ox}}}}={frac {[Red]}{[Ox]}}}

En equilibrio químico, la relación $Q r$ de la actividad del producto de reacción (a_Red) por la actividad del reactivo (a_Ox) es igual a la constante de equilibrio $K$ de la semirreacción:

{displaystyle K={frac {a_{text{Red}}}{a_{text{Ox}}}}}

La termodinámica estándar también dice que la energía libre real de Gibbs $Δ G$ está relacionada con el cambio de energía libre bajo el estado estándar $Δ G o$ por la relación:

{displaystyle Delta G=Delta G^{ominus }+RTln Q_{r}}

Q r

E

{displaystyle Delta G=-zFE.}

F

F = N A q

N A

q

{displaystyle E_{text{red}}=E_{text{red}}^{ominus }-{frac {RT}{zF}}ln Q_{r}=E_{text{red}}^{ominus }-{frac {RT}{zF}}ln {frac {a_{text{Red}}}{a_{text{Ox}}}}.}

{displaystyle E_{text{cell}}=E_{text{cell}}^{ominus }-{frac {RT}{zF}}ln Q_{r}}

donde:

$E rojo$ es el potencial de reducción de media célula a la temperatura de interés,
$E o rojo$ es el potencial estándar de reducción de media célula,
$E célula$ es el potencial celular (fuerza eléctrica) a la temperatura de interés,
$E o célula$ es el potencial celular estándar,
$R$ es la constante del gas universal: $R = 8.314 46261815324 J K -1 mol -1$ ,
$T$ es la temperatura en kelvins,
$z$ es el número de electrones transferidos en la reacción celular o media reacción,
$F$ es la constante Faraday, la magnitud de la carga (en coulombs) por topo de electrones: $F = 96485 .332 1233100184 C mol -1$ ,
$Q r$ es el cociente de reacción de la reacción celular, y
$a$ es la actividad química para la especie pertinente, donde $a Rojo$ es la actividad de la forma reducida y $a Ox$ es la actividad de la forma oxidada.

Tensión térmica

A temperatura ambiente (25 °C), tensión térmica ${displaystyle V_{T}={frac {RT}{F}}}$ es aproximadamente 25.693 mV. La ecuación Nernst se expresa con frecuencia en términos de logaritmos base-10 (i.e., logaritmos comunes) más que logaritmos naturales, en cuyo caso está escrito:

{displaystyle E=E^{ominus }-{frac {V_{T}}{z}}ln {frac {a_{text{Red}}}{a_{text{Ox}}}}=E^{ominus }-{frac {lambda V_{T}}{z}}log _{10}{frac {a_{text{Red}}}{a_{text{Ox}}}}.}

donde λ = ln(10) ≈ 2,3026 y λV_T ≈ 0,05916 voltios.

Formulario con coeficientes de actividad y concentraciones

Del mismo modo que las constantes de equilibrio, las actividades siempre se miden con respecto al estado estándar (1 ml para los solutos, 1 l para gases, y T = 298.15 K, i.e., 25 °C o 77 °F). La actividad química de una especie $i$ , $a i$ , está relacionado con la concentración medida $C i$ a través de la relación $a i = γ i C i$ , donde $γ i$ es el coeficiente de actividad de la especie $i$ . Debido a que los coeficientes de actividad tienden a la unidad en concentraciones bajas, o son desconocidos o difíciles de determinar a concentraciones medias y altas, las actividades en la ecuación de Nernst son frecuentemente reemplazadas por concentraciones simples y luego, potenciales de reducción estándar formal ${displaystyle E_{text{red}}^{ominus '}}$ usado.

Teniendo en cuenta los coeficientes de actividad ( $gamma$ ) la ecuación Nernst se convierte en:

{displaystyle E_{text{red}}=E_{text{red}}^{ominus }-{frac {RT}{zF}}ln left({frac {gamma _{text{Red}}}{gamma _{text{Ox}}}}{frac {C_{text{Red}}}{C_{text{Ox}}}}right)}

{displaystyle E_{text{red}}=E_{text{red}}^{ominus }-{frac {RT}{zF}}left(ln {frac {gamma _{text{Red}}}{gamma _{text{Ox}}}}+ln {frac {C_{text{Red}}}{C_{text{Ox}}}}right)}

{displaystyle E_{text{red}}=underbrace {left(E_{text{red}}^{ominus }-{frac {RT}{zF}}ln {frac {gamma _{text{Red}}}{gamma _{text{Ox}}}}right)} _{E_{text{red}}^{ominus '}}-{frac {RT}{zF}}ln {frac {C_{text{Red}}}{C_{text{Ox}}}}}

Donde el primer término incluye los coeficientes de actividad ( $gamma$ ) está denotado ${displaystyle E_{text{red}}^{ominus '}}$ y llamó al potencial formal de reducción estándar, de modo que ${displaystyle E_{text{red}}}$ se puede expresar directamente como una función ${displaystyle E_{text{red}}^{ominus '}}$ y las concentraciones en la forma más simple de la ecuación Nernst:

{displaystyle E_{text{red}}=E_{text{red}}^{ominus '}-{frac {RT}{zF}}ln {frac {C_{text{Red}}}{C_{text{Ox}}}}}

Potencial de reducción estándar formal

Cuando desea utilizar concentraciones simples en lugar de actividades, pero que los coeficientes de actividad están lejos de la unidad y ya no pueden ser descuidados y son desconocidos o demasiado difíciles de determinar, puede ser conveniente introducir la noción del "llamado" potencial de reducción formal estándar ( ${displaystyle E_{text{red}}^{ominus '}}$ ) que está relacionado con el potencial de reducción estándar como sigue:

{displaystyle E_{text{red}}^{ominus '}=E_{text{red}}^{ominus }-{frac {RT}{zF}}ln {frac {gamma _{text{Red}}}{gamma _{text{Ox}}}}}

{displaystyle E_{text{red}}=E_{text{red}}^{ominus '}-{frac {RT}{zF}}ln {frac {C_{text{Red}}}{C_{text{Ox}}}}}

Según Wenzel (2020), un potencial de reducción formal ${displaystyle E_{text{red}}^{ominus '}}$ es el potencial de reducción que se aplica a una media reacción bajo un conjunto de condiciones específicas tales como, por ejemplo, pH, fuerza iónica, o la concentración de agentes complejos.

El potencial de reducción formal ${displaystyle E_{text{red}}^{ominus '}}$ a menudo es una forma más conveniente, pero condicional, del potencial de reducción estándar, teniendo en cuenta los coeficientes de actividad y las características específicas de las condiciones del medio de reacción. Por lo tanto, su valor es un valor condicional, i.e., que depende de las condiciones experimentales y porque la fuerza iónica afecta a los coeficientes de actividad, ${displaystyle E_{text{red}}^{ominus '}}$ variará de media a media. En la literatura se pueden encontrar varias definiciones del potencial de reducción formal, dependiendo del objetivo perseguido y de las limitaciones experimentales impuestas por el sistema estudiado. La definición general ${displaystyle E_{text{red}}^{ominus '}}$ se refiere a su valor determinado cuando ${displaystyle {frac {C_{text{red}}}{C_{text{ox}}}}=1}$ . Un caso más particular es cuando ${displaystyle E_{text{red}}^{ominus '}}$ también se determina en pH 7, como por ejemplo para las reacciones redox importantes en sistemas bioquímicos o biológicos.

Determinación del potencial de reducción estándar formal cuando Cred/Cox = 1

The formal standard reduction potential ${displaystyle E_{text{red}}^{ominus '}}$ puede definirse como el potencial de reducción medida ${displaystyle E_{text{red}}}$ de la media reacción a la relación de concentración de unidad de las especies oxidadas y reducidas (i.e., cuando $C rojo / C Ox$ = 1) en condiciones dadas.

De hecho:

como, ${displaystyle E_{text{red}}=E_{text{red}}^{ominus }}$ , cuando ${displaystyle {frac {a_{text{red}}}{a_{text{ox}}}}=1}$ ,

{displaystyle E_{text{red}}=E_{text{red}}^{ominus '}}

, cuando

{displaystyle {frac {C_{text{red}}}{C_{text{ox}}}}=1}

porque ${displaystyle ln {1}=0}$ , y que el término ${displaystyle {frac {gamma _{text{red}}}{gamma _{text{ox}}}}}$ se incluye en ${displaystyle E_{text{red}}^{ominus '}}$ .

El potencial de reducción formal hace posible trabajar más simplemente con concentraciones molares (mol/L, M) o molares (mol/kg H2O, m) en lugar de actividades. Debido a que las concentraciones molares y molales alguna vez se denominaron concentraciones formales, podría explicar el origen del adjetivo formal en la expresión potencial formal.

El potencial formal es, por lo tanto, el potencial reversible de un electrodo en equilibrio inmerso en una solución donde los reactivos y los productos están en concentración unitaria. Si cualquier pequeño cambio incremental de potencial provoca un cambio en la dirección de la reacción, es decir, de reducción a oxidación o viceversa, el sistema está cerca del equilibrio, es reversible y es en su potencial formal. Cuando el potencial formal se mide en condiciones estándar (es decir, la actividad de cada especie disuelta es 1 mol/L, T = 298,15 K = 25 °C = 77 °F, $P gas$ = 1 bar) se convierte de facto en un potencial estándar.
Según Brown y Swift (1949):

"Un potencial formal se define como el potencial de una media célula, medida contra el electrodo de hidrógeno estándar, cuando la concentración total de cada estado de oxidación es un estado formal".

En este caso, en cuanto a los potenciales de reducción estándar, las concentraciones de especies disueltas permanecen iguales a un molar (M) o un molal (m), por lo que se dice que son uno formal (F). Entonces, expresando la concentración $C$ en molaridad $M$ (1 mol/L):

{displaystyle {frac {C_{text{red}}}{C_{text{ox}}}}={frac {1,mathrm {M} _{text{red}}}{1,mathrm {M} _{text{ox}}}}=1}

El término concentración formal (F) ahora se ignora en gran medida en la literatura actual y se puede asimilar comúnmente a la concentración molar (M) o la molalidad (m) en el caso de los cálculos termodinámicos.

El potencial formal también se encuentra a mitad de camino entre los dos picos en un voltamograma cíclico, donde en este punto la concentración de Ox (la especie oxidada) y Red (la especie reducida) en la superficie del electrodo son iguales.

Los coeficientes de actividad ${displaystyle gamma _{red}}$ y ${displaystyle gamma _{ox}}$ se incluyen en el potencial formal ${displaystyle E_{text{red}}^{ominus '}}$ , y porque dependen de condiciones experimentales como temperatura, fuerza iónica y pH, ${displaystyle E_{text{red}}^{ominus '}}$ no puede denominarse un potencial estándar inmutable, pero debe determinarse sistemáticamente para cada conjunto específico de condiciones experimentales.

Los potenciales de reducción formales se aplican para simplificar los cálculos de un sistema considerado bajo condiciones dadas e interpretación de medidas. Las condiciones experimentales en las que se determinan y su relación con los potenciales de reducción estándar deben describirse claramente para evitar confundirlos con los potenciales de reducción estándar.

Potencial de reducción estándar formal a pH 7

Potenciales de reducción estándar formal ( ${displaystyle E_{text{red}}^{ominus '}}$ ) también se utilizan comúnmente en bioquímica y biología celular para referirse a los potenciales de reducción estándar medidos en pH 7, un valor más cercano al pH de la mayoría de los fluidos fisiológicos e intracelulares que el pH de estado estándar de 0. La ventaja es definir una escala de redox más apropiada que la del estado estándar. Potenciales de reducción estándar formal ( ${displaystyle E_{text{red}}^{ominus '}}$ ) permite calcular más fácilmente si una reacción de redox se supone que ocurre en un proceso metabólico o para alimentar la actividad microbiana en algunas condiciones es factible o no.

Mientras que los potenciales de reducción estándar siempre se refieren al electrodo de hidrógeno estándar (SHE), con [H+] = 1 M correspondiente a un pH 0, y ${displaystyle E_{text{red H+}}^{ominus }}$ fijo arbitrariamente a cero por convención, ya no es el caso en un pH de 7. Entonces, el potencial de reducción ${displaystyle E_{text{red}}}$ de un electrodo de hidrógeno que opera al pH 7 es -0.413 V con respecto al electrodo de hidrógeno estándar (SHE).

Expresión de la ecuación de Nernst en función del pH

El $E_{h}$ y pH de una solución están relacionados por la ecuación Nernst como comúnmente representado por un diagrama Pourbaix () $E_{h}$ – pH plot). $E_{h}$ denota explícitamente ${displaystyle E_{text{red}}}$ expresado contra el electrodo de hidrógeno estándar (SHE). Para una ecuación de media célula, convencionalmente escrita como una reacción de reducción (i.e., electrones aceptados por un oxidante en el lado izquierdo):

<math alttext="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" xmlns="http://www.w3.org/1998/Math/MathML">aA+bB+hH++ze− − ↽ ↽ − − − − ⇀ ⇀ cC+dD{displaystyle a,A+b,B+h,{ce {H+}+z,e^{-}quad {ce {}quad c,C+d,D}<img alt="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/21d6729acf60e5eaffa170e8d2ef03fc0e334405" style="vertical-align: -0.505ex; width:41.61ex; height:2.843ex;"/>

El potencial de reducción estándar de media célula ${displaystyle E_{text{red}}^{ominus }}$ es dado por

{displaystyle E_{text{red}}^{ominus }({text{volt}})=-{frac {Delta G^{ominus }}{zF}}}

Donde $Delta G^{ominus }$ es el cambio de energía libre estándar Gibbs, $z$ es el número de electrones involucrados, y $F$ es la constante del Faraday. La ecuación Nernst relaciona pH y $E_{h}$ como sigue:

{displaystyle E_{h}=E_{text{red}}=E_{text{red}}^{ominus }-{frac {0.05916}{z}}log left({frac {{C}^{c}{D}^{d}}{{A}^{a}{B}^{b}}}right)-{frac {0.05916,h}{z}}{text{pH}}}

donde los corchetes indican actividades, y los exponentes se muestran de la manera convencional. Esta ecuación es la ecuación de una línea recta para ${displaystyle E_{text{red}}}$ como una función de pH con una pendiente de ${displaystyle -0.05916,left({frac {h}{z}}right)}$ volt (pH no tiene unidades).

Esta ecuación predice menor ${displaystyle E_{text{red}}}$ a valores de pH más altos. Esto se observa para la reducción de O₂ en H₂O, o OH⁻, y para la reducción de H⁺ en H₂. ${displaystyle E_{text{red}}}$ es entonces a menudo notado como $E_{h}$ para indicar que se refiere al electrodo de hidrógeno estándar (SHE) cuyo ${displaystyle E_{text{red}}}$ = 0 por convención bajo condiciones estándar (T = 298.15 K = 25 °C = 77 F, P_gas = 1 atm (1.013 bar), concentraciones = 1 M y por lo tanto pH = 0).

Principales factores que afectan los potenciales de reducción del estándar formal

El principal factor que afecta los potenciales de reducción formal en los procesos bioquímicos o biológicos suele ser el pH. Para determinar los valores aproximados de los potenciales de reducción formal, despreciando en una primera aproximación los cambios en los coeficientes de actividad debidos a la fuerza iónica, se debe aplicar la ecuación de Nernst cuidando de expresar primero la relación en función del pH. El segundo factor a considerar son los valores de las concentraciones tomadas en cuenta en la ecuación de Nernst. Para definir un potencial de reducción formal para una reacción bioquímica, siempre se debe indicar explícitamente el valor de pH, los valores de concentración y las hipótesis realizadas sobre los coeficientes de actividad. Al usar o comparar varios potenciales de reducción formales, también deben ser internamente consistentes.

Pueden surgir problemas al mezclar diferentes fuentes de datos usando diferentes convenciones o aproximaciones (es decir,, con diferentes hipótesis subyacentes). Cuando se trabaja en la frontera entre procesos inorgánicos y biológicos (p. ej., cuando se comparan procesos abióticos y bióticos en geoquímica cuando la actividad microbiana también podría estar presente en el sistema), se debe tener cuidado de no mezclar inadvertidamente los potenciales de reducción estándar versus SHE (pH = 0) con potenciales de reducción formales (pH = 7). Las definiciones deben expresarse claramente y controlarse cuidadosamente, especialmente si las fuentes de datos son diferentes y surgen de diferentes campos (p. ej., seleccionar y mezclar datos de libros de texto clásicos de electroquímica y microbiología sin prestar atención a las diferentes convenciones en las que se basan).

Ejemplos con un diagrama de Pourbaix

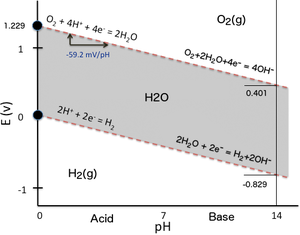
Diagrama de Pourbaix para agua, incluyendo regiones de estabilidad para agua, oxígeno e hidrógeno a temperatura y presión estándar (STP). La escala vertical (ordinada) es el potencial de electrodo relativo a un electrodo SHE. La escala horizontal (abscissa) es el pH del electrolito (otros no-interacting). Por encima de la línea superior, el oxígeno se deshará del electrodo hasta que el agua esté totalmente consumida. De la misma manera, debajo de la línea inferior el hidrógeno se desmoronará del electrodo hasta que el agua esté totalmente consumida.

Para ilustrar la dependencia del potencial de reducción del pH, uno puede simplemente considerar los dos equilibrios de oxidorreducción que determinan el dominio de estabilidad del agua en un diagrama de Pourbaix (E_h–gráfico de pH). Cuando el agua se somete a electrolisis aplicando una diferencia suficiente de potencial eléctrico entre dos electrodos sumergidos en agua, se produce hidrógeno en el cátodo (reducción de los protones del agua) mientras que se forma oxígeno en el ánodo (oxidación de los átomos de oxígeno del agua). Lo mismo puede ocurrir si un reductor más fuerte que el hidrógeno (p. ej., Na metálico) o un oxidante más fuerte que el oxígeno (p. ej., F₂) entra en contacto con el agua y reacciona con ella. En el E_h–pH plot aquí al lado (la versión más simple posible de un diagrama de Pourbaix), el dominio de estabilidad del agua (superficie gris) está delimitado en término de potencial redox por dos líneas discontinuas rojas inclinadas:

Línea de estabilidad inferior con evolución del gas hidrógeno debido a la reducción del protón en E muy bajo_h:

2 H + + 2 e - ⇌ H 2

(Cathode: reduction)

Línea de estabilidad más alta con evolución del gas de oxígeno debido a la oxidación del agua en muy alta E_h:

2 H 2 O 2 + 4 H + + 4 e -

(anodo: oxidación)

Al resolver la ecuación de Nernst para cada reacción de reducción correspondiente (es necesario revertir la reacción de oxidación del agua que produce oxígeno), ambas ecuaciones tienen una forma similar porque el número de protones y el número de electrones involucrados en una reacción son los mismos y su la relación es uno (2 H+/2 e⁻ para H ₂ y 4 H+/4 e⁻ con O2 respectivamente), por lo que se simplifica al resolver la ecuación de Nernst expresada en función del pH.

El resultado se puede expresar numéricamente de la siguiente manera:

{displaystyle E_{text{red}}=E_{text{red}}^{ominus }-0.05916 pH}

Tenga en cuenta que las pendientes de las dos líneas superior e inferior del dominio de estabilidad del agua son las mismas (-59,16 mV/unidad de pH), por lo que son paralelas en un diagrama de Pourbaix. Como las pendientes son negativas, a pH alto, la evolución de hidrógeno y oxígeno requiere un potencial de reducción mucho menor que a pH bajo.

Para la reducción de H⁺ a H₂, la relación mencionada anteriormente se convierte en:

{displaystyle E_{text{red}}=-0.05916 pH}

por convención

{displaystyle E_{text{red}}^{ominus }}

= 0 V para el electrodo de hidrógeno estándar (SHE: pH = 1).
Entonces, a pH = 7,

{displaystyle E_{text{red}}}

= 0,414 V para la reducción de protones.

Para la reducción de O₂ a 2 H₂O, la relación mencionada anteriormente se convierte en:

{displaystyle E_{text{red}}=1.229-0.05916 pH}

porque

{displaystyle E_{text{red}}^{ominus }}

= +1.229 V con respecto al electrodo de hidrógeno estándar (SHE: pH = 1).
Entonces, a pH = 7,

{displaystyle E_{text{red}}}

= +0,815 V para la reducción del oxígeno.

La compensación de -414 mV en ${displaystyle E_{text{red}}}$ es lo mismo para ambas reacciones de reducción porque comparten la misma relación lineal como una función de pH y las laderas de sus líneas son iguales. Esto se puede verificar directamente en un diagrama Pourbaix. Para otras reacciones de reducción, el valor del potencial de reducción formal en un pH de 7, comúnmente referido para reacciones bioquímicas, también depende de la pendiente de la línea correspondiente en un diagrama de Pourbaix i.e. la relación entre h.z del número de H+ al número de e⁻ involucrado en la reacción de reducción, y así en la estequiometría de la media reacción. La determinación del potencial de reducción formal en pH = 7 para una media reacción bioquímica determinada requiere así calcularlo con la ecuación Nernst correspondiente como función de pH. Uno no puede simplemente aplicar un offset de -414 mV a la E_h valor (SHE) cuando la relación h.z difiere de 1.

Aplicaciones en biología

Además de importantes reacciones redox en bioquímica y microbiología, la ecuación de Nernst también se usa en fisiología para calcular el potencial eléctrico de una membrana celular con respecto a un tipo de ion. Se puede vincular a la constante de disociación ácida.

Potencial de Nernst

La ecuación de Nernst tiene una aplicación fisiológica cuando se usa para calcular el potencial de un ion de carga $z$ a través de una membrana. Este potencial se determina utilizando la concentración del ion tanto dentro como fuera de la célula:

{displaystyle E={frac {RT}{zF}}ln {frac {[{text{ion outside cell}}]}{[{text{ion inside cell}}]}}=2.3026{frac {RT}{zF}}log _{10}{frac {[{text{ion outside cell}}]}{[{text{ion inside cell}}]}}.}

Cuando la membrana está en equilibrio termodinámico (es decir, sin flujo neto de iones) y si la célula es permeable a un solo ion, entonces el potencial de la membrana debe ser igual al potencial de Nernst para ese ion.

Ecuación de Goldman

Cuando la membrana es permeable a más de un ion, como es inevitablemente el caso, el potencial de reposo se puede determinar a partir de la ecuación de Goldman, que es una solución de la ecuación de entrada de G-H-K bajo las restricciones de que la densidad de corriente total impulsada por la fuerza electroquímica es cero:

{displaystyle E_{mathrm {m} }={frac {RT}{F}}ln {left({frac {displaystyle sum _{i}^{N}P_{mathrm {M} _{i}^{+}}left[mathrm {M} _{i}^{+}right]_{mathrm {out} }+displaystyle sum _{j}^{M}P_{mathrm {A} _{j}^{-}}left[mathrm {A} _{j}^{-}right]_{mathrm {in} }}{displaystyle sum _{i}^{N}P_{mathrm {M} _{i}^{+}}left[mathrm {M} _{i}^{+}right]_{mathrm {in} }+displaystyle sum _{j}^{M}P_{mathrm {A} _{j}^{-}}left[mathrm {A} _{j}^{-}right]_{mathrm {out} }}}right)},}

dónde

$E m$ es el potencial de la membrana (en voltios, equivalente a joules por coulomb),
$P ion$ es la permeabilidad de ese ion (en metros por segundo),
$[ion] Fuera.$ es la concentración extracelular de ese ión (en lunares por metro cúbico, para coincidir con las otras unidades SI, aunque las unidades estrictamente no importan, ya que los términos de concentración de ión se convierten en una relación sin dimensiones),
$[ion] dentro$ es la concentración intracelular de ese ión (en lunares por metro cúbico),
$R$ es la constante de gas ideal (joules per kelvin per mole),
$T$ es la temperatura en kelvins,
$F$ es la constante del Faraday (coulombs por topo).

El potencial a través de la membrana celular que se opone exactamente a la difusión neta de un ion particular a través de la membrana se denomina potencial de Nernst para ese ion. Como se vio anteriormente, la magnitud del potencial de Nernst está determinada por la relación de las concentraciones de ese ion específico en los dos lados de la membrana. Cuanto mayor sea esta relación, mayor será la tendencia del ion a difundirse en una dirección y, por lo tanto, mayor será el potencial de Nernst necesario para evitar la difusión. Existe una expresión similar que incluye $r$ (el valor absoluto de la relación de transporte). Esto tiene en cuenta a los transportistas con intercambios desiguales. Ver: bomba de sodio-potasio donde la relación de transporte sería 2/3, por lo que r es igual a 1,5 en la fórmula a continuación. La razón por la que insertamos un factor r = 1.5 aquí es que la densidad de corriente por la fuerza electroquímica J_e.c.(Na⁺) + J_e.c.(K⁺) ya no es cero, sino J_e.c.(Na⁺) + 1.5J_e.c.(K⁺) = 0 (ya que para ambos flujos de iones por fuerza electroquímica se compensa con el de la bomba, es decir, J_e.c. = −J_bomba), alterando las restricciones para aplicar la ecuación GHK. Las otras variables son las mismas que las anteriores. El siguiente ejemplo incluye dos iones: potasio (K⁺) y sodio (Na⁺). Se supone que el cloruro está en equilibrio.

{displaystyle E_{m}={frac {RT}{F}}ln {left({frac {rP_{mathrm {K} ^{+}}left[mathrm {K} ^{+}right]_{mathrm {out} }+P_{mathrm {Na} ^{+}}left[mathrm {Na} ^{+}right]_{mathrm {out} }}{rP_{mathrm {K} ^{+}}left[mathrm {K} ^{+}right]_{mathrm {in} }+P_{mathrm {Na} ^{+}}left[mathrm {Na} ^{+}right]_{mathrm {in} }}}right)}.}

Cuando se tiene en cuenta el cloruro (Cl⁻),

{displaystyle E_{m}={frac {RT}{F}}ln {left({frac {rP_{mathrm {K} ^{+}}left[mathrm {K} ^{+}right]_{mathrm {out} }+P_{mathrm {Na} ^{+}}left[mathrm {Na} ^{+}right]_{mathrm {out} }+P_{mathrm {Cl} ^{-}}left[mathrm {Cl} ^{-}right]_{mathrm {in} }}{rP_{mathrm {K} ^{+}}left[mathrm {K} ^{+}right]_{mathrm {in} }+P_{mathrm {Na} ^{+}}left[mathrm {Na} ^{+}right]_{mathrm {in} }+P_{mathrm {Cl} ^{-}}left[mathrm {Cl} ^{-}right]_{mathrm {out} }}}right)}.}

Derivación

Uso del factor de Boltzmann

Para simplificar, consideraremos una solución de moléculas redox activas que experimentan una reacción reversible de un electrón

Ox + e - Rojo

y que tienen un potencial estándar de cero, y en el que las actividades están bien representadas por las concentraciones (es decir, el coeficiente de actividad de la unidad). El potencial químico $μ c$ de esta solución es la diferencia entre las barreras de energía para tomar electrones y ceder electrones a el electrodo de trabajo que establece el potencial electroquímico de la solución. La proporción de moléculas oxidadas a reducidas, [Ox]/[Red], es equivalente a la probabilidad de ser oxidado (dando electrones) sobre la probabilidad de ser reducido (tomando electrones), que podemos escribir en términos del factor de Boltzmann para estos procesos:

{displaystyle {begin{aligned}{frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}&={frac {exp left(-[{text{barrier for gaining an electron}}]/kTright)}{exp left(-[{text{barrier for losing an electron}}]/kTright)}}\[6px]&=exp left({frac {mu _{mathrm {c} }}{kT}}right).end{aligned}}}

Tomando el logaritmo natural de ambos lados da

{displaystyle mu _{mathrm {c} }=kTln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}.}

Si $μ c \neq 0$ en [Ox]/[Rojo] = 1, necesitamos agregar esta constante adicional:

{displaystyle mu _{mathrm {c} }=mu _{mathrm {c} }^{ominus }+kTln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}.}

Dividiendo la ecuación por $e$ para convertir de potenciales químicos a potenciales de electrodo, y recordando que $k / e = R / F$ , obtenemos la ecuación de Nernst para el proceso de un electrón $Ox + e - ⇌ Red$ :

{displaystyle {begin{aligned}E&=E^{ominus }-{frac {kT}{e}}ln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}\&=E^{ominus }-{frac {RT}{F}}ln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}.end{aligned}}}

Uso de la termodinámica (potencial químico)

Las cantidades aquí se dan por molécula, no por mol, por lo que la constante de Boltzmann $k$ y la carga del electrón $e$ se utilizan en lugar de la constante de gas $R$ y la constante de Faraday F. Para convertir a las cantidades molares dadas en la mayoría de los libros de texto de química, simplemente es necesario multiplicar por la constante de Avogadro: $R = kN A$ y $F = eN A$ . La entropía de una molécula se define como

{displaystyle S {stackrel {mathrm {def} }{=}} kln Omega}

donde $Ω$ es el número de estados disponibles para la molécula. El número de estados debe variar linealmente con el volumen $V$ del sistema (aquí se considera un sistema idealizado para una mejor comprensión, por lo que las actividades se plantean muy cerca de las concentraciones verdaderas. La prueba estadística fundamental de la linealidad mencionada va más allá del alcance de esta sección, pero para ver que esto es cierto, es más simple considerar el proceso isotérmico habitual para un gas ideal donde el cambio de entropía $Δ S = nR ln(V 2 / V 1)$ se deduce de la definición de entropía y de la condición de temperatura constante y cantidad de gas $n$ que el cambio en el número de estados debe ser proporcional al cambio relativo en el volumen $V 2 / V 1$ . En este sentido, no hay diferencia en las propiedades estadísticas de los átomos de gases ideales en comparación con las especies disueltas de una solución con coeficientes de actividad iguales a uno: las partículas "flotan libremente" llenando el volumen proporcionado), que es inversamente proporcional a la concentración $c$ , por lo que también podemos escribir la entropía como

{displaystyle S=kln (mathrm {constant} times V)=-kln (mathrm {constant} times c).}

Por lo tanto, el cambio de entropía de un estado 1 a otro estado 2 es

{displaystyle Delta S=S_{2}-S_{1}=-kln {frac {c_{2}}{c_{1}}},}

{displaystyle S_{2}=S_{1}-kln {frac {c_{2}}{c_{1}}}.}

Si el estado 1 se encuentra en condiciones estándar, en las que $c 1$ es la unidad (por ejemplo, 1 atm o 1 M), simplemente cancelará las unidades de $c 2$ . Podemos, por lo tanto, escribir la entropía de una molécula arbitraria A como

{displaystyle S(mathrm {A})=S^{ominus }(mathrm {A})-kln[mathrm {A} ],}

{displaystyle S^{ominus }}

a

A +

b

B →

Sí.

Y +

z

entonces viene dado por

{displaystyle Delta S_{mathrm {rxn} }={big (}yS(mathrm {Y})+zS(mathrm {Z}){big)}-{big (}aS(mathrm {A})+bS(mathrm {B}){big)}=Delta S_{mathrm {rxn} }^{ominus }-kln {frac {[mathrm {Y} ]^{y}[mathrm {Z} ]^{z}}{[mathrm {A} ]^{a}[mathrm {B} ]^{b}}}.}

Definimos la relación en el último término como el cociente de reacción:

{displaystyle Q_{r}={frac {displaystyle prod _{j}a_{j}^{nu _{j}}}{displaystyle prod _{i}a_{i}^{nu _{i}}}}approx {frac {[mathrm {Z} ]^{z}[mathrm {Y} ]^{y}}{[mathrm {A} ]^{a}[mathrm {B} ]^{b}}},}

a j

. j

t

a . j j

E

E = μ c / e

E

Δ G

Δ G = zFE

n

F

Δ G

E

G = H - TS

H

T

{displaystyle Delta G=Delta H-TDelta S=Delta G^{ominus }+kTln Q_{r},}

{displaystyle E=E^{ominus }-{frac {kT}{ze}}ln Q_{r}.}

Esta es la forma más general de la ecuación de Nernst.

Para la reacción redox Ox + $z$ e⁻ → Rojo,

{displaystyle Q_{r}={frac {[mathrm {Red} ]}{[mathrm {Ox} ]}},}

{displaystyle {begin{aligned}E&=E^{ominus }-{frac {kT}{ze}}ln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}\&=E^{ominus }-{frac {RT}{zF}}ln {frac {[mathrm {Red} ]}{[mathrm {Ox} ]}}\&=E^{ominus }-{frac {RT}{zF}}ln Q_{r}.end{aligned}}}

El potencial celular a temperatura y presión estándar (STP) ${displaystyle E^{ominus }}$ a menudo se sustituye por el potencial formal ${displaystyle E^{ominus '}}$ , que incluye los coeficientes de actividad de las especies disueltas en condiciones experimentales dadas (T, P, fuerza iónica, pH y agentes complejos) y es el potencial que se mide en realidad en una célula electroquímica.

Relación con el equilibrio químico

La energía libre estándar Gibbs $Delta G^{ominus }$ está relacionado con la constante del equilibrio $K$ como sigue:

{displaystyle Delta G^{ominus }=-RTln {K}}

Al mismo tiempo, $Delta G^{ominus }$ es igual al producto de la carga total ( $zF$ ) transferido durante la reacción y el potencial celular ( ${displaystyle E_{cell}^{ominus }}$ ):

{displaystyle Delta G^{ominus }=-zFE_{cell}^{ominus }}

El signo es negativo, porque el sistema considerado realiza el trabajo y por lo tanto libera energía.

Entonces,

{displaystyle -zFE_{cell}^{ominus }=-RTln {K}}

Y por lo tanto:

{displaystyle E_{cell}^{ominus }={frac {RT}{zF}}ln {K}}

A partir de la ecuación de Nernst, también se puede demostrar la misma relación de forma inversa.

En el equilibrio químico, o equilibrio termodinámico, el potencial electroquímico $(E) = 0$ y por lo tanto el cociente de reacción ( $Q r$ ) alcanza el valor especial conocido como constante de equilibrio ( $K eq$ ):

Q r = K eq

Por lo tanto,

{displaystyle {begin{aligned}0&=E^{ominus }-{frac {RT}{zF}}ln K\{frac {RT}{zF}}ln K&=E^{ominus }\ln K&={frac {zFE^{ominus }}{RT}}end{aligned}}}

O en estado estándar,

{displaystyle log _{10}K={frac {zE^{ominus }}{lambda V_{T}}}={frac {zE^{ominus }}{0.05916{text{ V}}}}quad {text{at }}T=298.15~{text{K}}}

Hemos relacionado así el potencial de electrodo estándar y la constante de equilibrio de una reacción redox.

Limitaciones

En soluciones diluidas, la ecuación de Nernst se puede expresar directamente en términos de concentraciones (ya que los coeficientes de actividad están cerca de la unidad). Pero a concentraciones más altas, se deben usar las verdaderas actividades de los iones. Esto complica el uso de la ecuación de Nernst, ya que la estimación de actividades no ideales de iones generalmente requiere mediciones experimentales. La ecuación de Nernst solo se aplica cuando no hay flujo de corriente neta a través del electrodo. La actividad de los iones en la superficie del electrodo cambia cuando hay un flujo de corriente, y existen términos adicionales de sobrepotencial y pérdida resistiva que contribuyen al potencial medido.

A concentraciones muy bajas de los iones determinantes del potencial, el potencial predicho por la ecuación de Nernst se acerca a $\pm\infty$ . Esto no tiene sentido físico porque, en tales condiciones, la densidad de corriente de intercambio se vuelve muy baja y es posible que no haya un equilibrio termodinámico necesario para que se mantenga la ecuación de Nernst. El electrodo se llama no equilibrado en tal caso. Otros efectos tienden a controlar el comportamiento electroquímico del sistema, como la participación del electrón solvatado en la transferencia de electricidad y el equilibrio de los electrodos, tal como lo analizan Alexander Frumkin y B. Damaskin, Sergio Trasatti, etc.

Dependencia temporal del potencial

La expresión de la dependencia del tiempo ha sido establecida por Karaoglanoff.

Importancia en otros campos científicos

La ecuación de Nernst ha estado involucrada en la controversia científica sobre la fusión fría. Fleischmann y Pons, alegando que podría existir la fusión fría, calcularon que un cátodo de paladio sumergido en una celda de electrólisis de agua pesada podría alcanzar hasta 10²⁷ atmósferas de presión dentro de la red cristalina del metal del cátodo, suficiente presión para causar la fusión nuclear espontánea. En realidad, solo se lograron entre 10 000 y 20 000 atmósferas. El físico estadounidense John R. Huizenga afirmó que su cálculo original se vio afectado por una mala interpretación de la ecuación de Nernst. Citó un artículo sobre aleaciones de Pd-Zr.

La ecuación de Nernst permite el cálculo de la extensión de la reacción entre dos sistemas redox y se puede utilizar, por ejemplo, para evaluar si una reacción en particular se completará o no. En el equilibrio químico, las fuerzas electromotrices (fem) de las dos medias celdas son iguales. Esto permite calcular la constante de equilibrio $K$ de la reacción y, por lo tanto, la extensión de la reacción.

Contenido relacionado

Más resultados...