Dualidad onda-partícula

La dualidad onda-partícula es el concepto en mecánica cuántica de que cada partícula o entidad cuántica puede describirse como una partícula o una onda. Expresa la incapacidad de los conceptos clásicos "partícula" u "onda" para describir completamente el comportamiento de los objetos a escala cuántica. Como escribió Albert Einstein:

Parece como si debiéramos usar a veces una teoría ya veces la otra, mientras que a veces podemos usar cualquiera de las dos. Nos enfrentamos a un nuevo tipo de dificultad. Tenemos dos imágenes contradictorias de la realidad; por separado ninguno de ellos explica completamente los fenómenos de la luz, pero juntos lo hacen.

A través del trabajo de Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, Erwin Schrödinger y muchos otros, la teoría científica actual sostiene que todas las partículas exhiben una naturaleza ondulatoria y viceversa. Este fenómeno se ha verificado no solo para partículas elementales, sino también para partículas compuestas como átomos e incluso moléculas. Para las partículas macroscópicas, debido a sus longitudes de onda extremadamente cortas, las propiedades de las ondas generalmente no se pueden detectar.

Aunque el uso de la dualidad onda-partícula ha funcionado bien en física, el significado o interpretación no se ha resuelto satisfactoriamente; ver interpretaciones de la mecánica cuántica.

Bohr consideró la "paradoja de la dualidad" como un hecho fundamental o metafísico de la naturaleza. Un tipo dado de objeto cuántico exhibirá a veces carácter de onda, a veces de partícula, en entornos físicos respectivamente diferentes. Vio esa dualidad como un aspecto del concepto de complementariedad. Bohr consideró que la renuncia a la relación causa-efecto, o complementariedad, de la imagen del espacio-tiempo, era esencial para la descripción de la mecánica cuántica.

Werner Heisenberg consideró la pregunta más a fondo. Vio la dualidad como presente para todas las entidades cuánticas, pero no del todo en la descripción mecánica cuántica habitual considerada por Bohr. Lo vio en lo que se llama la segunda cuantización, que genera un concepto completamente nuevo de los campos que existen en el espacio-tiempo ordinario, siendo todavía visible la causalidad. Los valores de campo clásicos (p. ej., las intensidades de campo eléctrico y magnético de Maxwell) se reemplazan por un tipo de valor de campo completamente nuevo, como se considera en la teoría cuántica de campos. Dando la vuelta al razonamiento, la mecánica cuántica ordinaria se puede deducir como una consecuencia especializada de la teoría cuántica de campos.

Historia

Teorías clásicas de partículas y ondas de la luz.

Demócrito (siglo V a. C.) argumentó que todas las cosas en el universo, incluida la luz, están compuestas de subcomponentes indivisibles. Euclides (siglos IV-III a. C.) da tratados sobre la propagación de la luz, establece el principio de la trayectoria más corta de la luz, incluidos múltiples reflejos en espejos, incluidos los esféricos, mientras que Plutarco (siglos I-II d. C.) describe múltiples reflejos en espejos esféricos que discuten la creación de imágenes mayores o menores, reales o imaginarias, incluido el caso de quiralidad de las imágenes. A principios del siglo XI, el científico árabe Ibn al-Haytham escribió el primer Libro completo de Óptica.describe la reflexión, la refracción y el funcionamiento de una lente estenopeica a través de rayos de luz que viajan desde el punto de emisión hasta el ojo. Afirmó que estos rayos estaban compuestos de partículas de luz. En 1630, René Descartes popularizó la descripción de ondas opuestas en su tratado sobre la luz, El mundo, mostrando que el comportamiento de la luz podía recrearse modelando perturbaciones ondulatorias en un medio universal, es decir, el éter luminífero. A partir de 1670 y progresando durante tres décadas, Isaac Newton desarrolló y defendió su teoría corpuscular, argumentando que las líneas de reflexión perfectamente rectas demostraban la naturaleza de las partículas de la luz, solo las partículas podían viajar en tales líneas rectas. Explicó la refracción postulando que las partículas de luz se aceleraban lateralmente al entrar en un medio más denso. Casi al mismo tiempo, Newton' Los contemporáneos de Robert Hooke y Christiaan Huygens, y más tarde Augustin-Jean Fresnel, refinaron matemáticamente el punto de vista de la onda, mostrando que si la luz viajaba a diferentes velocidades en diferentes medios, la refracción podría explicarse fácilmente como la propagación de ondas de luz dependiente del medio. El principio de Huygens-Fresnel resultante fue extremadamente exitoso en la reproducción del comportamiento de la luz y posteriormente fue respaldado por el descubrimiento de Thomas Young de la interferencia de ondas de la luz mediante su experimento de doble rendija en 1801.La visión de ondas no desplazó inmediatamente a la visión de rayos y partículas, pero comenzó a dominar el pensamiento científico sobre la luz a mediados del siglo XIX, ya que podía explicar los fenómenos de polarización que las alternativas no podían.

James Clerk Maxwell descubrió que podía aplicar sus ecuaciones de Maxwell previamente descubiertas, junto con una ligera modificación para describir ondas autopropagantes de campos eléctricos y magnéticos oscilantes. Rápidamente se hizo evidente que la luz visible, la luz ultravioleta y la luz infrarroja eran ondas electromagnéticas de diferente frecuencia.

• Animación que muestra la dualidad onda-partícula con un experimento de doble rendija y efecto de un observador. Aumenta el tamaño para ver las explicaciones en el propio vídeo. Vea también un cuestionario basado en esta animación.
• Los impactos de partículas hacen visible el patrón de interferencia de las ondas.
• Una partícula cuántica está representada por un paquete de ondas.
• Interferencia de una partícula cuántica consigo misma.

Radiación de cuerpo negro y ley de Planck

En 1901, Max Planck publicó un análisis que logró reproducir el espectro observado de luz emitida por un objeto brillante. Para lograr esto, Planck tuvo que hacer una suposición matemática de la energía cuantificada de los osciladores, es decir, los átomos del cuerpo negro que emiten radiación. Einstein propuso más tarde que la radiación electromagnética en sí está cuantificada, no la energía de los átomos que la irradian.

La radiación de cuerpo negro, la emisión de energía electromagnética debido al calor de un objeto, no podía explicarse únicamente con argumentos clásicos. El teorema de equipartición de la mecánica clásica, la base de todas las teorías termodinámicas clásicas, establece que la energía de un objeto se reparte por igual entre los modos de vibración del objeto. Pero aplicar el mismo razonamiento a la emisión electromagnética de un objeto térmico de este tipo no tuvo tanto éxito. Hace tiempo que se sabe que los objetos térmicos emiten luz. Dado que se sabía que la luz eran ondas de electromagnetismo, los físicos esperaban describir esta emisión a través de leyes clásicas. Esto se conoció como el problema del cuerpo negro. Dado que el teorema de equipartición funcionó tan bien para describir los modos de vibración del propio objeto térmico, era natural suponer que funcionaría igualmente bien al describir la emisión radiativa de tales objetos. Pero rápidamente surgió un problema si cada modo recibía una partición igual de energía, los modos de longitud de onda corta consumirían toda la energía. Esto quedó claro al trazar la ley de Rayleigh-Jeans, que, mientras predecía correctamente la intensidad de las emisiones de longitud de onda larga, predecía una energía total infinita a medida que la intensidad diverge al infinito para longitudes de onda cortas. Esto se conoció como la catástrofe ultravioleta. energía total infinita predicha a medida que la intensidad diverge al infinito para longitudes de onda cortas. Esto se conoció como la catástrofe ultravioleta. energía total infinita predicha a medida que la intensidad diverge al infinito para longitudes de onda cortas. Esto se conoció como la catástrofe ultravioleta.

En 1900, Max Planck planteó la hipótesis de que la frecuencia de la luz emitida por el cuerpo negro dependía de la frecuencia del oscilador que la emitía, y la energía de estos osciladores aumentaba linealmente con la frecuencia (según E = hf donde h es la constante de Planck y fes la frecuencia). Esta no era una propuesta poco sólida considerando que los osciladores macroscópicos operan de manera similar cuando se estudian cinco osciladores armónicos simples de igual amplitud pero diferente frecuencia, el oscilador con la frecuencia más alta posee la energía más alta (aunque esta relación no es lineal como la de Planck). Al exigir que la luz de alta frecuencia sea emitida por un oscilador de igual frecuencia, y al requerir además que este oscilador ocupe mayor energía que uno de menor frecuencia, Planck evitó cualquier catástrofe, dando una partición igual a los osciladores de alta frecuencia producidos sucesivamente menos osciladores y menos luz emitida. Y como en la distribución de Maxwell-Boltzmann, los osciladores de baja frecuencia y baja energía fueron suprimidos por la avalancha de sacudidas térmicas de los osciladores de mayor energía.

El aspecto más revolucionario del tratamiento de Planck del cuerpo negro es que se basa inherentemente en un número entero de osciladores en equilibrio térmico con el campo electromagnético. Estos osciladores entregan toda su energía al campo electromagnético, creando un cuanto de luz, cada vez que son excitados por el campo electromagnético, absorbiendo un cuanto de luz y comenzando a oscilar a la frecuencia correspondiente. Planck había creado intencionalmente una teoría atómica del cuerpo negro, pero sin querer había generado una teoría atómica de la luz, en la que el cuerpo negro nunca genera cuantos de luz a una frecuencia determinada con una energía inferior a hf. Sin embargo, una vez que se dio cuenta de que había cuantificado el campo electromagnético, denunció las partículas de luz como una limitación de su aproximación, no como una propiedad de la realidad.

Efecto fotoeléctrico

Si bien Planck había resuelto la catástrofe ultravioleta mediante el uso de átomos y un campo electromagnético cuantizado, la mayoría de los físicos contemporáneos estaban de acuerdo en que los "cuantos de luz" de Planck representaban solo fallas en su modelo. Una derivación más completa de la radiación del cuerpo negro produciría un campo electromagnético completamente continuo y "similar a una onda" sin cuantificación. Sin embargo, en 1905, Albert Einstein tomó el modelo de cuerpo negro de Planck para producir su solución a otro problema destacado de la época: el efecto fotoeléctrico, en el que los átomos emiten electrones cuando absorben energía de la luz. Desde que se teorizó su existencia ocho años antes, los fenómenos se habían estudiado con el modelo electrónico en mente en laboratorios de física de todo el mundo.

En 1902, Philipp Lenard descubrió que la energía de estos electrones expulsados ​​no dependía de la intensidad de la luz incidente, sino de su frecuencia. Entonces, si uno hace brillar una pequeña luz de baja frecuencia sobre un metal, se expulsan algunos electrones de baja energía. Si ahora se proyecta un haz muy intenso de luz de baja frecuencia sobre el mismo metal, se expulsa una gran cantidad de electrones; sin embargo, poseen la misma baja energía, simplemente hay más de ellos. Cuanta más luz hay, más electrones se expulsan. Mientras que para obtener electrones de alta energía, se debe iluminar el metal con luz de alta frecuencia. Al igual que la radiación de cuerpo negro, esto estaba en desacuerdo con una teoría que invocaba la transferencia continua de energía entre la radiación y la materia. Sin embargo, todavía se puede explicar usando una descripción completamente clásica de la luz,

Si uno usara los cuantos de energía de Planck y exigiera que la radiación electromagnética a una frecuencia dada solo pudiera transferir energía a la materia en múltiplos enteros de un cuanto de energía hf, entonces el efecto fotoeléctrico podría explicarse de manera muy simple. La luz de baja frecuencia solo expulsa electrones de baja energía porque cada electrón es excitado por la absorción de un solo fotón. Aumentar la intensidad de la luz de baja frecuencia (aumentar la cantidad de fotones) solo aumenta la cantidad de electrones excitados, no su energía, porque la energía de cada fotón permanece baja. Solo aumentando la frecuencia de la luz y, por lo tanto, aumentando la energía de los fotones, se pueden expulsar electrones con mayor energía. Por lo tanto, usando la constante h de Planckpara determinar la energía de los fotones en función de su frecuencia, la energía de los electrones expulsados ​​también debería aumentar linealmente con la frecuencia, siendo el gradiente de la línea la constante de Planck. Estos resultados no se confirmaron hasta 1915, cuando Robert Andrews Millikan produjo resultados experimentales en perfecto acuerdo con las predicciones de Einstein.

Si bien la energía de los electrones expulsados ​​​​reflejó la constante de Planck, la existencia de fotones no se demostró explícitamente hasta el descubrimiento del efecto antiagrupamiento de fotones. Esto se refiere a la observación de que una vez que un solo emisor (un átomo, molécula, emisor de estado sólido, etc.) irradia una señal de luz detectable, no puede liberar inmediatamente una segunda señal hasta después de que el emisor haya sido reexcitado. Esto conduce a un retraso de tiempo cuantificable estadísticamente entre las emisiones de luz, por lo que la detección de múltiples señales se vuelve cada vez más improbable a medida que el tiempo de observación cae por debajo del tiempo de vida del estado excitado del emisor. El efecto se puede demostrar en un laboratorio de nivel universitario.

Este fenómeno solo podría explicarse a través de fotones. Los "cuantos de luz" de Einstein no se llamarían fotones hasta 1925, pero incluso en 1905 representaban el ejemplo por excelencia de la dualidad onda-partícula. La radiación electromagnética se propaga siguiendo ecuaciones de onda lineales, pero solo puede ser emitida o absorbida como elementos discretos, actuando así como una onda y una partícula simultáneamente.

La explicación de Einstein del efecto fotoeléctrico

En 1905, Albert Einstein proporcionó una explicación del efecto fotoeléctrico, un experimento que la teoría ondulatoria de la luz no logró explicar. Lo hizo postulando la existencia de fotones, cuantos de energía luminosa con cualidades de partículas.

En el efecto fotoeléctrico, se observó que hacer brillar una luz sobre ciertos metales conduciría a una corriente eléctrica en un circuito. Presumiblemente, la luz estaba sacando electrones del metal, haciendo que la corriente fluyera. Sin embargo, usando el caso del potasio como ejemplo, también se observó que mientras que una luz azul tenue era suficiente para causar una corriente, incluso la luz roja más fuerte y brillante disponible con la tecnología de la época no causaba ninguna corriente. De acuerdo con la teoría clásica de la luz y la materia, la fuerza o amplitud de una onda de luz era proporcional a su brillo: una luz brillante debería haber sido lo suficientemente fuerte como para crear una gran corriente. Sin embargo, curiosamente, esto no fue así.

Einstein explicó este enigma postulando que los electrones pueden recibir energía de un campo electromagnético solo en unidades discretas (cuantos o fotones): una cantidad de energía E que estaba relacionada con la frecuencia f de la luz por

donde h es la constante de Planck (6,626 × 10 Js). Solo los fotones de una frecuencia lo suficientemente alta (por encima de un cierto valor de umbral) podrían liberar un electrón. Por ejemplo, los fotones de luz azul tenían suficiente energía para liberar un electrón del metal, pero los fotones de luz roja no. Un fotón de luz por encima de la frecuencia umbral podría liberar solo un electrón; cuanto mayor sea la frecuencia de un fotón, mayor será la energía cinética del electrón emitido, pero ninguna cantidad de luz por debajo de la frecuencia umbral podría liberar un electrón. Violar esta ley requeriría láseres de altísima intensidad que aún no se habían inventado. Los fenómenos dependientes de la intensidad ahora se han estudiado en detalle con tales láseres.

Einstein recibió el Premio Nobel de Física en 1921 por su descubrimiento de la ley del efecto fotoeléctrico.

La hipótesis de de Broglie

En 1924, Louis-Victor de Broglie formuló la hipótesis de de Broglie, afirmando que toda la materia tiene una naturaleza ondulatoria, relacionó la longitud de onda y el momento:

Esta es una generalización de la ecuación de Einstein anterior, ya que el momento de un fotón viene dado por p = y la longitud de onda (en el vacío) por λ = , donde c es la velocidad de la luz en el vacío.

La fórmula de De Broglie se confirmó tres años más tarde para electrones con la observación de la difracción de electrones en dos experimentos independientes. En la Universidad de Aberdeen, George Paget Thomson pasó un haz de electrones a través de una delgada película de metal y observó los patrones de interferencia predichos. En Bell Labs, Clinton Joseph Davisson y Lester Halbert Germer guiaron el haz de electrones a través de una rejilla cristalina en su experimento conocido popularmente como experimento de Davisson-Germer.

De Broglie recibió el Premio Nobel de Física en 1929 por su hipótesis. Thomson y Davisson compartieron el Premio Nobel de Física en 1937 por su trabajo experimental.

Principio de incertidumbre de Heisenberg

En su trabajo sobre la formulación de la mecánica cuántica, Werner Heisenberg postuló su principio de incertidumbre, que establece:

dóndeaquí indica desviación estándar, una medida de dispersión o incertidumbre;x y p son la posición y el momento lineal de una partícula, respectivamente.es la constante de Planck reducida (la constante de Planck dividida por 2 ).

Heisenberg originalmente explicó esto como una consecuencia del proceso de medición: medir la posición con precisión perturbaría el impulso y viceversa, ofreciendo un ejemplo (el "microscopio de rayos gamma") que dependía crucialmente de la hipótesis de De Broglie. Sin embargo, ahora se piensa que esto solo explica parcialmente el fenómeno, pero que la incertidumbre también existe en la propia partícula, incluso antes de que se realice la medición.

De hecho, la explicación moderna del principio de incertidumbre, que amplía la interpretación de Copenhague propuesta por primera vez por Bohr y Heisenberg, depende aún más centralmente de la naturaleza ondulatoria de una partícula. Así como no tiene sentido discutir la ubicación precisa de una onda en una cuerda, las partículas no tienen posiciones perfectamente precisas; del mismo modo, así como no tiene sentido discutir la longitud de onda de una onda de "pulso" que viaja a lo largo de una cuerda, las partículas no tienen momentos perfectamente precisos que correspondan a la inversa de la longitud de onda. Además, cuando la posición está relativamente bien definida, la onda es similar a un pulso y tiene una longitud de onda y, por lo tanto, un impulso muy mal definidos. Y a la inversa, cuando el momento y, por lo tanto, la longitud de onda están relativamente bien definidos, la onda parece larga y sinusoidal y, por lo tanto, tiene una posición muy mal definida.

Teoría de Broglie-Bohm

El propio De Broglie había propuesto una construcción de onda piloto para explicar la dualidad onda-partícula observada. Desde este punto de vista, cada partícula tiene una posición y un momento bien definidos, pero está guiada por una función de onda derivada de la ecuación de Schrödinger. La teoría de la onda piloto fue inicialmente rechazada porque generaba efectos no locales cuando se aplicaba a sistemas que involucraban más de una partícula. Sin embargo, la no localidad pronto se estableció como una característica integral de la teoría cuántica y David Bohm amplió el modelo de de Broglie para incluirla explícitamente.

En la representación resultante, también llamada teoría de Broglie-Bohm o mecánica de Bohm, la dualidad onda-partícula se desvanece y explica el comportamiento de la onda como una dispersión con apariencia de onda, porque el movimiento de la partícula está sujeto a una ecuación guía o potencial cuántico.

Esta idea me parece tan natural y simple, para resolver el dilema onda-partícula de una manera tan clara y ordinaria, que es un gran misterio para mí que haya sido tan generalmente ignorada. – JSBell

La mejor ilustración del modelo de onda piloto fue proporcionada por los experimentos de "gotas ambulantes" de Couder de 2010, que demuestran el comportamiento de la onda piloto en un análogo mecánico macroscópico.

Naturaleza ondulatoria de objetos grandes.

Desde las demostraciones de propiedades ondulatorias en fotones y electrones, se han realizado experimentos similares con neutrones y protones. Entre los experimentos más famosos se encuentran los de Estermann y Otto Stern en 1929. Los autores de experimentos recientes similares con átomos y moléculas, que se describen a continuación, afirman que estas partículas más grandes también actúan como ondas.

En la década de 1970 se llevó a cabo una serie dramática de experimentos que enfatizaban la acción de la gravedad en relación con la dualidad onda-partícula utilizando el interferómetro de neutrones. Los neutrones, uno de los componentes del núcleo atómico, proporcionan gran parte de la masa de un núcleo y, por lo tanto, de la materia ordinaria. En el interferómetro de neutrones, actúan como ondas mecánicas cuánticas sujetas directamente a la fuerza de la gravedad. Si bien los resultados no fueron sorprendentes, ya que se sabía que la gravedad actuaba sobre todo, incluida la luz (véanse las pruebas de relatividad general y el experimento de caída de fotones de Pound-Rebka), la autointerferencia de la onda mecánica cuántica de un fermión masivo en un campo gravitatorio nunca antes se había confirmado experimentalmente.

En 1999, se informó sobre la difracción de fullerenos C ₆₀ por parte de investigadores de la Universidad de Viena. Los fullerenos son objetos comparativamente grandes y masivos, con una masa atómica de alrededor de 720 u. La longitud de onda de De Broglie del haz incidente fue de aproximadamente 2,5 pm, mientras que el diámetro de la molécula es de aproximadamente 1 nm, unas 400 veces mayor. En 2012, estos experimentos de difracción de campo lejano podrían extenderse a las moléculas de ftalocianina y sus derivados más pesados, que se componen de 58 y 114 átomos respectivamente. En estos experimentos, la acumulación de dichos patrones de interferencia se pudo registrar en tiempo real y con sensibilidad de una sola molécula.

En 2003, el grupo de Viena también demostró la naturaleza ondulatoria de la tetrafenilporfirina, un biocolorante plano con una extensión de aproximadamente 2 nm y una masa de 614 u. Para esta demostración emplearon un interferómetro Talbot Lau de campo cercano. En el mismo interferómetro también encontraron franjas de interferencia para C ₆₀ F ₄₈, una bola de bucky fluorada con una masa de unas 1600 u, compuesta por 108 átomos. Las moléculas grandes ya son tan complejas que dan acceso experimental a algunos aspectos de la interfase cuántica-clásica, es decir, a ciertos mecanismos de decoherencia. En 2011, la interferencia de moléculas tan pesadas como 6910 u pudo demostrarse en un interferómetro Kapitza-Dirac-Talbot-Lau.En 2013 se ha demostrado la interferencia de moléculas por encima de las 10.000 u.

Si los objetos más pesados ​​que la masa de Planck (aproximadamente el peso de una bacteria grande) tienen una longitud de onda de De Broglie es teóricamente poco claro y experimentalmente inalcanzable; por encima de la masa de Planck, la longitud de onda Compton de una partícula sería más pequeña que la longitud de Planck y su propio radio de Schwarzschild, una escala en la que las teorías actuales de la física pueden colapsar o necesitar ser reemplazadas por otras más generales.

Couder, Fort, et al. mostró que las gotas de aceite macroscópicas en un baño de fluido vibrante pueden usarse como un modelo analógico de dualidad onda-partícula; una gota localizada crea un campo de ondas periódicas a su alrededor. La interacción resonante entre la gota y su propio campo de ondas exhibe un comportamiento análogo al de las partículas cuánticas: interferencia en el experimento de doble rendija, tunelización impredecible (dependiendo de manera complicada del estado prácticamente oculto del campo), cuantización de la órbita (esa partícula tiene que 'encontrar una resonancia ' con las perturbaciones de campo que crea (después de una órbita, su fase interna tiene que volver al estado inicial) y el efecto Zeeman. Tenga en cuenta que otros experimentos de rendija simple y doblehan demostrado que las interacciones pared-gota en lugar de la difracción o la interferencia de la onda piloto pueden ser responsables de los patrones hidrodinámicos observados, que son diferentes de los patrones de interferencia inducidos por hendiduras que exhiben las partículas cuánticas.

Importancia

La dualidad onda-partícula está profundamente arraigada en los fundamentos de la mecánica cuántica. En el formalismo de la teoría, toda la información sobre una partícula está codificada en su función de onda, una función de valores complejos análoga a la amplitud de una onda en cada punto del espacio. Esta función evoluciona según la ecuación de Schrödinger. Para partículas con masa esta ecuación tiene soluciones que siguen la forma de la ecuación de onda. La propagación de tales ondas conduce a fenómenos ondulatorios como la interferencia y la difracción. Las partículas sin masa, como los fotones, no tienen soluciones de la ecuación de Schrödinger. En lugar de una función de onda de partículas que localiza la masa en el espacio, se puede construir una función de onda de fotones a partir de la cinemática de Einstein para localizar la energía en coordenadas espaciales.

El comportamiento similar a una partícula es más evidente debido a los fenómenos asociados con la medición en la mecánica cuántica. Al medir la ubicación de la partícula, la partícula se verá forzada a un estado más localizado según el principio de incertidumbre. Cuando se ve a través de este formalismo, la medición de la función de onda conducirá aleatoriamente al colapso de la función de onda a una función marcadamente máxima en algún lugar. Para partículas con masa, la probabilidad de detectar la partícula en cualquier ubicación particular es igual al cuadrado de la amplitud de la función de onda allí. La medición devolverá una posición bien definida y está sujeta al principio de incertidumbre de Heisenberg.

Tras el desarrollo de la teoría cuántica de campos, la ambigüedad desapareció. El campo permite soluciones que siguen la ecuación de onda, que se denominan funciones de onda. El término partícula se usa para etiquetar las representaciones irreducibles del grupo de Lorentz que son permitidas por el campo. Una interacción como en un diagrama de Feynman se acepta como una aproximación conveniente desde el punto de vista del cálculo, donde se sabe que los tramos salientes son simplificaciones de la propagación y las líneas internas son, en algún orden, una expansión de la interacción del campo. Dado que el campo es no local y está cuantificado, se explican los fenómenos que antes se consideraban paradojas. Dentro de los límites de la dualidad onda-partícula, la teoría cuántica de campos da los mismos resultados.

Visualización

Hay dos formas de visualizar el comportamiento onda-partícula: por el modelo estándar y por la teoría de de Broglie-Bohr.

A continuación se muestra una ilustración de la dualidad onda-partícula en relación con la hipótesis de De Broglie y el principio de incertidumbre de Heisenberg, en términos de funciones de onda espaciales de posición y momento para una partícula sin espín con masa en una dimensión. Estas funciones de onda son transformadas de Fourier entre sí.

Cuanto más localizada sea la función de onda del espacio de posición, más probable es que la partícula se encuentre con las coordenadas de posición en esa región y, en consecuencia, la función de onda del espacio de momento está menos localizada, por lo que los posibles componentes de momento que podría tener la partícula están más extendidos.

Por el contrario, cuanto más localizada sea la función de onda espacio-momento, más probable es que la partícula se encuentre con esos valores de componentes de momento en esa región y, en consecuencia, menos localizada será la función de onda espacio-posición, por lo que las coordenadas de posición que podría ocupar la partícula son más extendida.

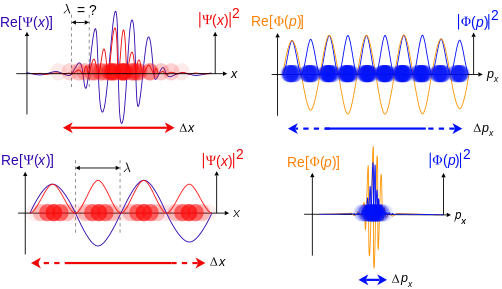Funciones de onda de posición

x y momento

p correspondientes a partículas cuánticas. La opacidad del color de las partículas corresponde a la densidad de probabilidad de encontrar la partícula con posición

x o componente de momento

p.

Arriba: Si se desconoce la longitud de onda

λ, también lo son el momento

p, el vector de onda

k y la energía

E (relaciones de De Broglie). Como la partícula está más localizada en el espacio de posiciones, Δ

x es menor que para Δ

p _x.

Abajo: si se conoce

λ, también se conocen

p,

k y

mi _ Como la partícula está más localizada en el espacio de cantidad de movimiento, Δ

p es menor que para Δ

x.

Vistas alternativas

La dualidad onda-partícula es un enigma constante en la física moderna. La mayoría de los físicos aceptan la dualidad onda-partícula como la mejor explicación para una amplia gama de fenómenos observados; sin embargo, no está exento de controversia. Aquí también se presentan puntos de vista alternativos. Estos puntos de vista generalmente no son aceptados por la física convencional, pero sirven como base para una valiosa discusión dentro de la comunidad.

Vista de partículas y ondas

El modelo de onda piloto fue desarrollado originalmente por Louis de Broglie y desarrollado posteriormente por David Bohm en la teoría de la variable oculta. La frase "variable oculta" es engañosa ya que la variable en cuestión son las posiciones de las partículas. En lugar de dualidad, el modelo de onda piloto propone que tanto la onda como la partícula están presentes con la onda guiando a la partícula de manera determinista. La onda en cuestión es la función de onda que obedece a la ecuación de Schrödinger. La formulación de Bohm pretende ser clásica, pero tiene que incorporar una característica claramente no clásica: una fuerza no local ("potencial cuántico") que actúa sobre las partículas.

El propósito original de Bohm (1952) “era mostrar que una alternativa a la interpretación de Copenhague es al menos lógicamente posible. Poco después dejó el proyecto a un lado y no lo revivió hasta que conoció a Basil Hiley en 1961 cuando ambos estaban en el Birbeck College (Universidad de Londres). Bohm y Hiley luego escribieron extensamente sobre la teoría y ganó una audiencia más amplia. Esta idea es sostenida por una minoría significativa dentro de la comunidad física.

El experimento de Afshar (2007) puede sugerir que es posible observar simultáneamente las propiedades de ondas y partículas de los fotones. Sin embargo, esta afirmación es cuestionada por otros científicos.

Vista de solo onda

Carver Mead, un científico estadounidense y profesor de Caltech, dijo que la dualidad puede ser reemplazada por una vista de "solo onda". En su libro Collective Electrodynamics: Quantum Foundations of Electromagnetism (2000), Mead pretende analizar el comportamiento de los electrones y fotones puramente en términos de funciones de onda de electrones, y atribuye el aparente comportamiento de partículas a efectos de cuantización y estados propios. Según el crítico David Haddon:

Mead ha cortado el nudo gordiano de la complementariedad cuántica. Afirma que los átomos, con sus neutrones, protones y electrones, no son partículas en absoluto, sino puras ondas de materia. Mead cita como prueba evidente de la naturaleza exclusivamente ondulatoria tanto de la luz como de la materia el descubrimiento entre 1933 y 1996 de diez ejemplos de fenómenos de ondas puras, incluido el omnipresente láser de los reproductores de CD, las corrientes eléctricas de autopropagación de los superconductores y el Bose –Condensado de átomos de Einstein.

Albert Einstein, quien, en su búsqueda de una Teoría del Campo Unificado, no aceptaba la dualidad onda-partícula, escribió:

Esta doble naturaleza de la radiación (y de los corpúsculos materiales)... ha sido interpretada por la mecánica cuántica de una manera ingeniosa y asombrosamente exitosa. Esta interpretación... me parece sólo una salida temporal...

La interpretación de muchos mundos (MWI) a veces se presenta como una teoría de solo ondas, incluso por su creador, Hugh Everett, quien se refirió a MWI como "la interpretación de ondas".

losLa hipótesis de las tres ondas de R. Horodecki relaciona la partícula con la onda. La hipótesis implica que una partícula masiva es un fenómeno ondulatorio intrínsecamente espacial y temporalmente extendido por una ley no lineal.

losLa teoría del colapso determinista considera el colapso y la medición como dos procesos físicos independientes. El colapso ocurre cuando dos paquetes de ondas se superponen espacialmente y satisfacen un criterio matemático, que depende de los parámetros de ambos paquetes de ondas. Es una contracción del volumen superpuesto. En un aparato de medición, uno de los dos paquetes de ondas es uno de los grupos atómicos, que constituyen el aparato, y los paquetes de ondas colapsan como máximo hasta el volumen de dicho grupo. Esto imita la acción de una partícula puntual.

Vista de solo partículas

Todavía en los días de la antigua teoría cuántica, William Duane fue pionero en una versión pre-mecánica cuántica de la dualidad onda-partícula, y otros, incluido Alfred Landé, la desarrollaron. Duane explicó la difracción de rayos X por un cristal en términos únicamente de su aspecto de partícula. La desviación de la trayectoria de cada fotón difractado se explica como debida a la transferencia de momento cuantificado de la estructura espacialmente regular del cristal de difracción.

Vista de ni onda ni partícula

Se ha argumentado que nunca hay partículas u ondas exactas, sino sólo algún compromiso o intermedio entre ellas. Por esta razón, en 1928 Arthur Eddington acuñó el nombre de " ondulación " para describir los objetos, aunque hoy en día no se usa con regularidad. Una consideración es que los puntos matemáticos de dimensión cero no se pueden observar. Otra es que la representación formal de tales puntos, la función delta de Dirac, no es física, porque no se puede normalizar. Los argumentos paralelos se aplican a los estados de onda puros. Roger Penrose afirma:

Tales 'estados de posición' son funciones de onda idealizadas en el sentido opuesto de los estados de impulso. Mientras que los estados de momento están infinitamente dispersos, los estados de posición están infinitamente concentrados. Tampoco es normalizable [...].

Usos

Aunque es difícil trazar una línea que separe la dualidad onda-partícula del resto de la mecánica cuántica, es posible enumerar algunas aplicaciones de esta idea básica.

• La dualidad onda-partícula se explota en la microscopía electrónica, donde las pequeñas longitudes de onda asociadas con el electrón se pueden usar para ver objetos mucho más pequeños que lo que es visible con luz visible.
• De manera similar, la difracción de neutrones usa neutrones con una longitud de onda de alrededor de 0,1 nm, el espaciado típico de los átomos en un sólido, para determinar la estructura de los sólidos.
• Las fotos ahora pueden mostrar esta naturaleza dual, lo que puede conducir a nuevas formas de examinar y registrar este comportamiento.