Dualidad (matemáticas)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En matemáticas, a dualidad traduce conceptos, teoremas o estructuras matemáticas en otros conceptos, teoremas o estructuras de una manera única, a menudo (pero no siempre) por medio de una operación de involución: si el doble de $A$ es $B$ , entonces el dual de $B$ es $A$ . Tales involuciones a veces tienen puntos fijos, de modo que el doble de $A$ es $A$ en sí mismo. Por ejemplo, el teorema de Desargues es auto-dual en este sentido bajo dualidad estándar en geometría proyectiva.

En contextos matemáticos, dualidad tiene numerosos significados. Se ha descrito como "un concepto muy generalizado e importante en las matemáticas (modernas)" y "un tema general importante que tiene manifestaciones en casi todas las áreas de las matemáticas".

Muchas dualidades matemáticas entre objetos de dos tipos corresponden a emparejamientos, funciones bilineales de un objeto de un tipo y otro objeto del segundo tipo a alguna familia de escalares. Por ejemplo, la dualidad del álgebra lineal corresponde de esta manera a mapas bilineales de pares de espacios vectoriales a escalares, la dualidad entre distribuciones y las funciones de prueba asociadas corresponde al emparejamiento en el que uno integra una distribución contra una función de prueba, y la dualidad de Poincaré corresponde de manera similar al número de intersección, visto como un emparejamiento entre subvariedades de una variedad dada.

Desde el punto de vista de la teoría de categorías, la dualidad también puede verse como un funtor, al menos en el ámbito de los espacios vectoriales. Este funtor asigna a cada espacio su espacio dual, y la construcción pullback asigna a cada flecha $f : V \to W$ es dual $f * : W * \to V *$ .

Ejemplos introductorios

En palabras de Michael Atiyah,

La dualidad en las matemáticas no es un teorema, sino un "principio".

La siguiente lista de ejemplos muestra las características comunes de muchas dualidades, pero también indica que el significado preciso de dualidad puede variar de un caso a otro.

Complemento de un subconjunto

Una dualidad simple, quizás la más simple, surge al considerar subconjuntos de un conjunto fijo $S$ . A cualquier subconjunto $A \subseteq S, el complemento A c consta de todos aquellos elementos en S que no están contenidos en A . Es nuevamente un subconjunto de S . Tomar el complemento tiene las siguientes propiedades:$

Aplicarlo dos veces devuelve el conjunto original, es decir, $() A c) c = A$ . Esto se refiere diciendo que la operación de tomar el complemento es un involution.
Una inclusión de conjuntos $A \subseteq B$ se convierte en una inclusión en opuesto dirección $B c \subseteq A c$ .
Dados dos subconjuntos $A$ y $B$ de $S$ , $A$ figura en $B c$ si $B$ figura en $A c$ .

Esta dualidad aparece en topología como una dualidad entre subconjuntos abiertos y cerrados de algún espacio topológico fijo $X$ : un subconjunto $U$ de $X$ está cerrado si y sólo si su complemento en $X$ está abierto. Debido a esto, muchos teoremas sobre conjuntos cerrados son duales con respecto a los teoremas sobre conjuntos abiertos. Por ejemplo, cualquier unión de conjuntos abiertos es abierta, por lo que dualmente, cualquier intersección de conjuntos cerrados es cerrada. El interior de un conjunto es el conjunto abierto más grande que contiene, y el cierre del conjunto es el conjunto cerrado más pequeño que lo contiene. Debido a la dualidad, el complemento del interior de cualquier conjunto $U$ es igual al cierre del complemento de $U$ .

Doble cono

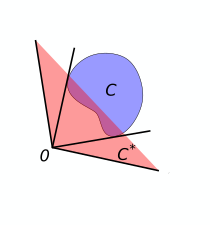
Una dualidad en geometría es proporcionada por la construcción de doble cono. Dado un conjunto ${displaystyle C}$ de puntos en el plano ${displaystyle mathbb {R} {2}}$ (o puntos más generalmente en ${displaystyle mathbb {R} {} {}} {fn}}$ ), el cono dual se define como el conjunto ${displaystyle C^{*}subseteq mathbb {R}$ consistentes en esos puntos ${displaystyle (x_{1},x_{2}}$ satisfacción

{displaystyle x_{1}c_{1}+x_{2}c_{2}geq 0}

{displaystyle (c_{1},c_{2}}

{displaystyle C}

{displaystyle C}

{displaystyle C^{}

{displaystyle C}

{displaystyle C}

Aplicar la operación dos veces devuelve un conjunto posiblemente más grande: para todos ${displaystyle C}$ , ${displaystyle C}$ figura en ${displaystyle C^{}$ . (Para algunos) ${displaystyle C}$ , a saber, los conos, los dos son en realidad iguales.)

Las otras dos propiedades se mantienen sin cambios:

Todavía es cierto que una inclusión ${displaystyle Csubseteq D}$ se convierte en una inclusión en la dirección opuesta ( ${displaystyle D^{*}subseteq C^{*}$ ).
Dados dos subconjuntos ${displaystyle C}$ y ${displaystyle D}$ del avión, ${displaystyle C}$ figura en ${displaystyle D^{*}$ si ${displaystyle D}$ figura en ${displaystyle C^{*}$ .

Espacio vectorial dual

Un ejemplo muy importante de una dualidad surge en álgebra lineal asociando a cualquier espacio vectorial $V$ su espacio vectorial dual $V *$ . Sus elementos son las funcionalidades lineales ${displaystyle varphi: Vto K}$ , donde $K$ es el campo sobre el cual $V$ se define. Las tres propiedades del cono dual llevan a este tipo de dualidad reemplazando subconjuntos de ${displaystyle mathbb {R} {2}}$ por espacio vectorial e inclusiones de tales subconjuntos por mapas lineales. Es decir:

Aplicar la operación de tomar el espacio vectorial dual dos veces da otro espacio vectorial $V #$ . Siempre hay un mapa $V \to V #$ . Para algunos $V$ , es decir, precisamente los espacios vectoriales de dimensión finita, este mapa es un isomorfismo.
Un mapa lineal $V \to W$ da lugar a un mapa en la dirección opuesta ( $W * \to V *$ ).
Dados dos espacios vectoriales $V$ y $W$ , los mapas de $V$ a $W *$ corresponde a los mapas de $W$ a $V *$ .

Una característica particular de esta dualidad es que $V$ y $V *$ son isomórficos para ciertos objetos, es decir, espacios vectoriales de dimensión finita. Sin embargo, en cierto sentido esto es una coincidencia afortunada, ya que dar tal isomorfismo requiere una cierta elección, por ejemplo la elección de una base de $V< /lapso>. Esto también es cierto en el caso de que V sea un espacio de Hilbert, a través de el teorema de representación de Riesz.$

Teoría de Galois

En todas las dualidades discutidas anteriormente, la dualidad de un objeto es del mismo tipo que el objeto mismo. Por ejemplo, la dualidad de un espacio vectorial es otra vez un espacio vectorial. Muchas declaraciones de dualidad no son de este tipo. En cambio, tales dualidades revelan una estrecha relación entre objetos de naturaleza aparentemente diferente. Un ejemplo de tal dualidad más general es de la teoría de Galois. Para una extensión Galois fija $K / F$ , uno puede asociar el grupo Galois $Gal(K / E)$ a cualquier campo intermedio $E$ (es decir, $F \subseteq E \subseteq K$ ). Este grupo es un subgrupo del grupo Galois $G = Gal(K / F)$ . Por el contrario, a cualquier subgrupo $H \subseteq G$ hay el campo fijo $K H$ compuesto por elementos fijos por los elementos en $H$ .

En comparación con lo anterior, esta dualidad tiene las siguientes características:

Una extensión $F \subseteq F .$ de campos intermedios da lugar a la inclusión de los grupos Galois en la dirección opuesta: $Gal(K / F') \subseteq Gal(K / F)$ .
Asociación $Gal(K / E)$ a $E$ y $K H$ a $H$ son inversos entre sí. Este es el contenido del teorema fundamental de la teoría de Galois.

Dualidades de inversión de orden

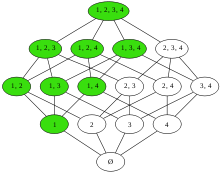
Diagrama de Hasse del conjunto de potencia ${1,2,3,4}$ , parcialmente ordenado por $\subset$ . La doble pose, es decir, ordenando $.$ , se obtiene girando el diagrama hacia abajo. Los nodos verdes forman un conjunto superior y un conjunto inferior en el orden original y dual, respectivamente.

Dado un poset $P = (X, \leq)$ (abreviatura de conjunto parcialmente ordenado; es decir, un conjunto que tiene una noción de orden pero en el que dos elementos no necesariamente pueden colocarse en orden entre sí), el poset dual $P d = (< var style="padding-right: 1px;">X, \geq)$ comprende el mismo conjunto de bases pero la relación inversa. Ejemplos familiares de órdenes parciales duales incluyen

las relaciones de subconjunto y superconjunto $\subset$ y $.$ en cualquier colección de conjuntos, como los subconjuntos de un conjunto fijo $S$ . Esto da lugar al primer ejemplo de una dualidad mencionada anteriormente.
el divideciones y múltiples relaciones en los enteros.
el descendiente de y antepasado de relaciones en el conjunto de humanos.

Una transformación de dualidad es un antiautomorfismo involutivo $f$ de un conjunto parcialmente ordenado $S$ , es decir, una involución de inversión de orden $f : S \to S$ . En varios casos importantes, estas propiedades simples determinan la transformación de forma única hasta algunas simetrías simples. Por ejemplo, si $f 1$ , $f 2$ son dos transformaciones de dualidad, entonces su composición es un automorfismo de orden de $S$ ; por lo tanto, dos transformaciones de dualidad cualesquiera difieren sólo por un automorfismo de orden. Por ejemplo, todos los automorfismos de orden de un conjunto de potencias $S = 2 R$ son inducidos por permutaciones de $R$ .

Un concepto definido para un orden parcial $P$ corresponderá a un concepto dual en el orden dual poset $P d$ . Por ejemplo, un elemento mínimo de $P$ será un elemento máximo de $P d$ : minimalidad y maximalidad son conceptos duales en Teoría del orden. Otros pares de conceptos duales son límites superior e inferior, conjuntos inferiores y conjuntos superiores, e ideales y filtros.

En topología, los conjuntos abiertos y los conjuntos cerrados son conceptos duales: el complemento de un conjunto abierto es cerrado y viceversa. En la teoría matroide, la familia de conjuntos complementarios a los conjuntos independientes de una matroide determinada forman otra matroide, llamada matroide dual.

Dualidades que invierten dimensiones

Hay muchas dualidades distintas pero interrelacionadas en las que los objetos geométricos o topológicos corresponden a otros objetos del mismo tipo, pero con una inversión de las dimensiones de las características de los objetos. Un ejemplo clásico de esto es la dualidad de los sólidos platónicos, en la que el cubo y el octaedro forman un par dual, el dodecaedro y el icosaedro forman un par dual y el tetraedro es autodual. El poliedro dual de cualquiera de estos poliedros puede formarse como la cáscara convexa de los puntos centrales de cada cara del poliedro primario, de modo que los vértices del poliedro dual se corresponden uno a uno con las caras del poliedro primario. De manera similar, cada arista del dual corresponde a una arista del primal, y cada cara del dual corresponde a un vértice del primal. Estas correspondencias preservan la incidencia: si dos partes del poliedro primario se tocan, también lo hacen las dos partes correspondientes del poliedro dual. De manera más general, utilizando el concepto de reciprocidad polar, cualquier poliedro convexo, o más generalmente cualquier politopo convexo, corresponde a un poliedro dual o politopo dual, con un $i$ dimensional de un politopo $n$ dimensional correspondiente a un $(n - i - 1)$ -característica dimensional del dual politopo. La naturaleza de la dualidad que preserva la incidencia se refleja en el hecho de que las redes frontales de los poliedros o politopos primarios y duales son en sí mismos duales de teoría de orden. La dualidad de politopos y la dualidad de la teoría del orden son ambas involuciones: el politopo dual del politopo dual de cualquier politopo es el politopo original, y al invertir todas las relaciones de orden dos veces se regresa al orden original. La elección de un centro de polaridad diferente conduce a politopos duales geométricamente diferentes, pero todos tienen la misma estructura combinatoria.

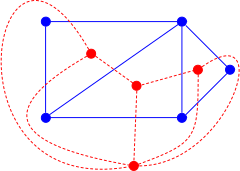
A partir de cualquier poliedro tridimensional, se puede formar un gráfico plano, el gráfico de sus vértices y aristas. El poliedro dual tiene una gráfica dual, una gráfica con un vértice por cada cara del poliedro y con una arista por cada dos caras adyacentes. El mismo concepto de dualidad de gráfico plano puede generalizarse a gráficos que se dibujan en el plano pero que no provienen de un poliedro tridimensional, o más generalmente a incrustaciones de gráficos en superficies de género superior: se puede dibujar un gráfico dual colocando un vértice dentro de cada región delimitada por un ciclo de bordes en la incrustación y dibujando un borde que conecta dos regiones cualesquiera que comparten un borde límite. Un ejemplo importante de este tipo proviene de la geometría computacional: la dualidad para cualquier conjunto finito $S$ de puntos en el plano entre la triangulación de Delaunay de $S$ y el diagrama de Voronoi de $S$ . Al igual que con los poliedros duales y los politopos duales, la dualidad de los gráficos en las superficies es una involución de inversión de dimensiones: cada vértice en el gráfico incrustado primario corresponde a una región de la incrustación dual, cada borde en el primario es atravesado por un borde en el dual, y cada región del primal corresponde a un vértice del dual. El gráfico dual depende de cómo está incrustado el gráfico primario: diferentes incrustaciones planas de un solo gráfico pueden conducir a diferentes gráficos duales. La dualidad matroide es una extensión algebraica de la dualidad del gráfico plano, en el sentido de que la matroide dual de la matroide gráfica de un gráfico plano es isomorfa a la matroide gráfica del gráfico dual.

Una especie de dualidad geométrica también ocurre en la teoría de la optimización, pero no una que revierte las dimensiones. Un programa lineal puede ser especificado por un sistema de variables reales (las coordenadas para un punto en el espacio Euclideano ${displaystyle mathbb {R} {} {}} {fn}}$ ), un sistema de limitaciones lineales (especifique que el punto se encuentra en un medio espacio; la intersección de estos espacios es un politopo convexo, la región factible del programa), y una función lineal (lo que optimizar). Cada programa lineal tiene un doble problema con la misma solución óptima, pero las variables en el doble problema corresponden a limitaciones en el problema primario y viceversa.

Dualidad en lógica y teoría de conjuntos

En lógica, funciones o relaciones $A$ y $B$ se consideran duales si $A (\neg x) = \neg B (x)< /span>, donde \neg es la negación lógica. La dualidad básica de este tipo es la dualidad de los cuantificadores \exists y \forall en la lógica clásica. Estos son duales porque \exists x .\neg P (x) y \neg\forall x . P (x) son equivalentes para todos los predicados P en lógica clásica: si existe un x para el cual P no se cumple, entonces es falso que P se cumpla para todos los x (pero lo contrario no se cumple constructivamente). De esta dualidad lógica fundamental se derivan varias otras:$

Se dice que una fórmula es satisfizo en un determinado modelo si hay asignaciones a sus variables libres que lo hacen realidad; es válido si cada uno la asignación a sus variables libres lo hace realidad. La satisfacción y la validez son duales porque las fórmulas inválidas son precisamente aquellas cuyas negaciones son satisfechas, y las fórmulas insaciables son aquellas cuyas negaciones son válidas. Esto se puede ver como un caso especial del tema anterior, con los cuantificadores que van más allá de las interpretaciones.
En la lógica clásica, $\land$ y $Alternativa$ los operadores son duales en este sentido, porque $(x \land \neg Sí.)$ y $\neg x Alternativa Sí.)$ son equivalentes. Esto significa que para cada teorema de la lógica clásica hay un teorema dual equivalente. Las leyes de De Morgan son ejemplos. Más generalmente, $\land (x i) = Alternativa x i$ . El lado izquierdo es verdadero si y sólo si $О i \neg x i$ , y el lado derecho si y sólo si ¬i.x_i.
En la lógica modal, $. p$ significa que la proposición $p$ es "necesariamente" verdad, y $Cause p$ que $p$ es "posiblemente" cierto. La mayoría de las interpretaciones de la lógica modal asignan significados duales a estos dos operadores. Por ejemplo en Kripke semantics, " $p$ es posiblemente cierto" significa "hay algún mundo $W$ tales que $p$ es verdad $W$ ", mientras " $p$ es necesariamente cierto" significa "para todos los mundos $W$ , $p$ es verdad $W$ ". La dualidad de $.$ y $Cause$ entonces sigue de la dualidad analógica $О$ y $\exists$ . Otros operadores duales se comportan de forma similar. Por ejemplo, la lógica temporal tiene operadores que denotan "será cierto en algún momento en el futuro" y "será verdad en todo momento en el futuro" que son igualmente duales.

Otras dualidades análogas se derivan de estas:

La unión teórica y la intersección son duales bajo el operador de complementos $\cdot C$ . Eso es, $A C \cap B C = A \cup B) C$ , y más generalmente, $\cap A C α = \cup A α) C$ . Esto se deriva de la dualidad $О$ y $\exists$ : un elemento $x$ es miembro de $\cap A C α$ si $О α \neg x ▪ A α$ , y es miembro de $() \cup A α) C$ si $\neg α . x ▪ A α$ .

Objetos dobles

Un grupo de dualidades se puede describir dotándole, para cualquier objeto matemático $X$ , del conjunto de morfismos $Hom (X, D)$ en algunos objeto fijo $D$ , con una estructura similar a la de $X$ . A esto a veces se le llama Hom interno. En general, esto produce una verdadera dualidad sólo para elecciones específicas de $D$ , en cuyo caso $< var style="padding-right: 1px;">X * = Hom (X, D)$ se conoce como el dual de $X$ . Siempre hay una aplicación de $X$ al bidual, es decir, el dual del doble,

{displaystyle Xto X^{**}:=(X^{*})^{*}=operatorname {Hom} (operatorname {Hom} (X,D),D). }

x ▪ X

f : X \to D

Hom(X, D)

f () x)

X

Nuevos espacios vectoriales

La construcción del espacio vectorial dual

{displaystyle V^{*}=operatorname {Hom} (V,K)}

V \to V #

V

Isomorfismos de V y V∗ y espacios producto internos

Un espacio vectorial $V$ es isomorfo a $V *< /sup>$ precisamente si $V$ es de dimensión finita. En este caso, tal isomorfismo es equivalente a una forma bilineal no degenerada.

{displaystyle varphi:Vtimes Vto K}

V

K

V

n

() n - k)

Dualidad en geometría proyectiva

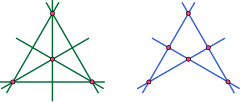
El cuadrángulo completo, una configuración de cuatro puntos y seis líneas en el plano proyector (izquierda) y su configuración dual, el cuadrilátero completo, con cuatro líneas y seis puntos (derecha).

En algunos planos proyectivos, es posible encontrar transformaciones geométricas que asignan cada punto del plano proyectivo a una línea, y cada línea del plano proyectivo a un punto, de manera que se preserve la incidencia. Para tales planos surge un principio general de dualidad en planos proyectivos: dado cualquier teorema en dicha geometría proyectiva plana, intercambiar los términos "punto" y "línea" en todas partes resulta en un teorema nuevo e igualmente válido. Un ejemplo simple es que la afirmación "dos puntos determinan una línea única, la línea que pasa por estos puntos" es una línea única. tiene la doble afirmación de que "dos líneas determinan un punto único, el punto de intersección de estas dos líneas". Para obtener más ejemplos, consulte Teoremas duales.

Una explicación conceptual de este fenómeno en algunos planos (sobre todo aviones de campo) es ofrecida por el espacio vectorial dual. De hecho, los puntos en el plano proyectivo ${displaystyle mathbb {RP}$ corresponde a espacios subvectorales unidimensionales ${displaystyle Vsubset mathbb {R} ^{3}$ mientras que las líneas en el plano proyectivo corresponden a espacios subvectorales ${displaystyle W.$ de la dimensión 2. La dualidad en estas geometrías proyectivas se deriva de la asignación a una dimensión única ${displaystyle V}$ el subespacio ${displaystyle (mathbb {R} } {}}} {}}}$ consistentes en esos mapas lineales ${displaystyle f:mathbb {R} ^{3}to mathbb {R}$ que satisfacen ${displaystyle f(V)=0}$ . Como consecuencia de la fórmula de dimensión del álgebra lineal, este espacio es bidimensional, es decir, corresponde a una línea en el plano proyectivo asociado a ${displaystyle (mathbb {R} } {}}} {}}}$ .

La forma bilineal (definida positiva)

{displaystyle langle cdotcdot rangle:mathbb {R} ^{3}times mathbb {R} ^{3}to mathbb {R}langle x,yrangle =sum ¿Qué?

{displaystyle mathbb {RP}

{displaystyle Vsubset mathbb {R} ^{3}

{displaystyle left{in mathbb {R} ^{3},langle v,wrangle =0{text{ for all }vin Vright}

Espacios vectoriales topológicos y espacios de Hilbert

En el ámbito de los espacios vectoriales topológicos existe una construcción similar, reemplazando la dual por el espacio vectorial dual topológico. Hay varias nociones de espacio dual topológico, y cada una de ellas da lugar a un cierto concepto de dualidad. Un espacio vectorial topológico ${displaystyle X}$ que es canónicamente isomorfo a su bidual ${displaystyle X'}$ se llama un espacio reflexivo:

{displaystyle Xcong X'''.}

Ejemplos:

Como en el caso finito-dimensional, en cada espacio Hilbert $H$ su producto interior $Negociación, \cdot$ define un mapa ${displaystyle Hto H^{*},vmapsto (wmapsto langle w,vrangle),}$ que es una bijeción debido al teorema de representación Riesz. Como corolario, cada espacio de Hilbert es un espacio reflexivo de Banach.
El espacio doble de un espacio Lp es $L q$ Donde $1/ p + 1/ q = 1$ siempre que $1 \leq p ■$ , pero el doble $L JUEGO$ es más grande que $L 1$ . Por lo tanto $L 1$ no es reflexivo.
Las distribuciones son funcionales lineales en espacios adecuados de funciones. Son un medio técnico importante en la teoría de las ecuaciones diferenciales parciales (PDE): en lugar de resolver un PDE directamente, puede ser más fácil primero resolver el PDE en el "sentido débil", es decir, encontrar una distribución que satisface el PDE y, segundo, mostrar que la solución debe, de hecho, ser una función. Todos los espacios estándar de distribuciones — ${displaystyle {mathcal {}'(U)}$ , ${displaystyle {Mathcal {S}'(mathbb {R} } {n}}$ , ${displaystyle {mathcal {} {infty}(U)}$ — son espacios reflexivos localmente convexos.

Más objetos duales

La red dual de una red $L$ está dada por

{displaystyle operatorname {Hom} (L,mathbf {Z}),}

{displaystyle operatorname {Hom} (G,S^{1}),}

Categorías duales

Categoría opuesta y funtores adjuntos

En otro grupo de dualidades, los objetos de una teoría se traducen en objetos de otra teoría y los mapas entre objetos en la primera teoría se traducen en morfismos en la segunda teoría, pero con la dirección invertida. Usando el lenguaje de la teoría de categorías, esto equivale a un funtor contravariante entre dos categorías $C$ y $D$ :

F : C \to D

que para dos objetos cualesquiera X y Y de C da un mapa

Hom C () X, Y) \to Hom D () F () Y), F () X)

Ese functor puede o no ser una equivalencia de categorías. Hay varias situaciones en las que dicho funtor es una equivalencia entre la categoría opuesta $C op$ de $C$ y $D$ . Utilizando una dualidad de este tipo, cada afirmación de la primera teoría puede traducirse en una dualidad "dual". afirmación de la segunda teoría, donde la dirección de todas las flechas debe invertirse. Por lo tanto, cualquier dualidad entre las categorías $C$ y $D$ es formalmente lo mismo que una equivalencia entre $C$ y $D op$ ( $C< /var> op$ y $D$ ). Sin embargo, en muchas circunstancias las categorías opuestas no tienen un significado inherente, lo que hace de la dualidad un concepto adicional y separado.

Una categoría que equivale a su doble se llama auto-dual. Un ejemplo de categoría autodual es la categoría de espacios Hilbert.

Muchas nociones de teoría de categorías vienen en pares en el sentido de que se corresponden entre sí al considerar la categoría opuesta. Por ejemplo, productos cartesianos $Y 1 \times Y 2$ y uniones disjuntas $Y < sub>1 ⊔ Y 2$ de conjuntos son duales entre sí en el sentido de que

Hom X, Y 1 \times Y 2 ♪ = Hom () X, Y 1) \times Hom (X, Y 2)

Hom Y 1 ⊔ Y 2, X ♪ = Hom () Y 1, X) \times Hom (Y 2, X)

para cualquier conjunto $X$ . Este es un caso particular de un fenómeno de dualidad más general, bajo el cual los límites de una categoría $C$ corresponden a colimits en la categoría opuesta $C operaciones$ ; otros ejemplos concretos de esto son epimorfismos vs. monomorfismo, en particular módulos de factor (o grupos, etc.) vs. submodules, productos directos vs. sumas directas (también llamados coproductos para enfatizar el aspecto de la dualidad). Por consiguiente, en algunos casos, las pruebas de ciertas declaraciones pueden reducirse a la mitad, utilizando ese fenómeno de dualidad. Otras nociones relacionadas con tal dualidad categórica son módulos proyectivos e inyectables en álgebra homológica, fibras y cofibraciones en topología y categorías de modelos más generalmente.

Dos funtores $F : C \to D$ y $G : D \to C$ son adjuntos si para todos los objetos c en C y d en D

Hom D (F) c), d ♪♪ C () c, G () d)

de una manera natural. En realidad, la correspondencia de límites y límites es un ejemplo de adjoints, ya que hay una adjunción

colim: C I Administración C : Δ

entre el functor colimit que asigna a cualquier diagrama en $C$ indexado por alguna categoría $I$ su colimit y el functor diagonal que mapea cualquier objeto $c$ de $C$ al diagrama constante que tiene $c$ en todos los lugares. Dualmente,

Δ: C Administración C I : lim

Espacios y funciones

La dualidad Gelfand es una dualidad entre los álgebras C* conmutativas A espacios compactos Hausdorff X es el mismo: se asigna a X el espacio de funciones continuas (que desaparecen al infinito) X a CLos números complejos. Por el contrario, el espacio X puede ser reconstruido A como el espectro de A. Tanto Gelfand como Pontryagin dualidad pueden deducirse de una forma en gran medida formal, teórica de categoría.

De manera similar, existe una dualidad en la geometría algebraica entre anillos conmutativos y esquemas afines: para cada anillo conmutativo A hay un espectro afín, Spec A. Por el contrario, dado un esquema afín S, se recupera un anillo tomando secciones globales de la estructura gavilla O_S. Además, los homomorfismos de anillo están en correspondencia uno a uno con los morfismos de esquemas afines, por lo que existe una equivalencia

(Anillos conmutativos)^operaciones (programas de affines)

Los esquemas afines son los componentes básicos de los esquemas locales. Por tanto, el resultado anterior dice que la teoría local de esquemas es lo mismo que el álgebra conmutativa, el estudio de anillos conmutativos.

La geometría no conmutativa se inspira en la dualidad de Gelfand y estudia las álgebras C* no conmutativas como si fueran funciones en algún espacio imaginado. La dualidad Tannaka-Krein es un análogo no conmutativo de la dualidad Pontryagin.

Conexiones Galois

En varias situaciones, las dos categorías que son duales entre sí en realidad surgen de conjuntos parcialmente ordenados, es decir, existe cierta noción de que un objeto "siendo más pequeño" que otro. Una dualidad que respeta los ordenamientos en cuestión se conoce como conexión de Galois. Un ejemplo es la dualidad estándar en la teoría de Galois mencionada en la introducción: corresponde una extensión de campo mayor, bajo el mapeo que asigna a cualquier extensión L ⊃ K (dentro de una extensión fija mayor). campo Ω) el grupo de Galois Gal (Ω / L) —a un grupo más pequeño.

La colección de todos los subconjuntos abiertos de un espacio topológico X forma un álgebra de Heyting completa. Existe una dualidad, conocida como dualidad de Piedra, que conecta espacios sobrios y lugares espaciales.

El teorema de representación de Birkhoff relacionó celos distributivos y órdenes parciales

Dualidad de Pontryagin

La dualidad de Pontryagin da una dualidad en la categoría de grupos abelianos localmente compactos: dado cualquier grupo G, el grupo de caracteres

χ(G♪ = Hom ()G, S¹)

dado por homomorfismos de grupo continuos desde G al grupo circular S¹ puede estar dotado de la topología compacta-abierta. La dualidad de Pontryagin establece que el grupo de caracteres es nuevamente abeliano localmente compacto y que

G χ(χ)G)).

Además, los grupos discretos corresponden a grupos abelianos compactos; los grupos finitos corresponden a grupos finitos. Por un lado, Pontryagin es un caso especial de la dualidad de Gelfand. Por otro lado, es la razón conceptual del análisis de Fourier, ver más abajo.

Dualidades analíticas

En el análisis, los problemas se resuelven frecuentemente pasando a la descripción dual de funciones y operadores.

La transformada de Fourier cambia entre funciones en un espacio vectorial y su dual:

{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

{displaystyle f(x)=int _{-infty }{infty }{widehat {f}(xi) e^{2pi ixxi },dxi.}

fRR^N

{displaystyle {f}}

{displaystyle f(-x)={widehat {widehat {f}}(x)}

RR^NRe^−2πix

La transformación Laplace es similar a Fourier transforma e intercambia operadores de multiplicación por polinomios con operadores diferenciales lineales de coeficiente constante.
La transformación legendaria es una importante dualidad analítica que cambia entre velocidades en mecánica lagrangiana y momenta en mecánica Hamiltoniana.

Homología y cohomología

Los teoremas que muestran que ciertos objetos de interés son espacios duales (en el sentido del álgebra lineal) de otros objetos de interés a menudo se denominan dualidades. Muchas de estas dualidades están dadas por un par bilineal de dos espacios vectoriales K

A ⊗ B → K.

Para emparejamientos perfectos, existe, por tanto, un isomorfismo de A al dual de B.

Dualidad de Poincaré

La dualidad de Poincaré de una variedad compleja compacta y suave X está dada por un emparejamiento de cohomología singular con coeficientes C (de manera equivalente, cohomología de gavilla de la gavilla constante C)

Hⁱ(X) ⊗ H²ⁿ⁻ⁱ(X) → C,

donde n es la dimensión (compleja) de X. La dualidad de Poincaré también se puede expresar como una relación de homología singular y cohomología de Rham, afirmando que el mapa

{displaystyle (gammaomega)mapsto int _{gamma }omega }

(integrar una forma diferencial k sobre un ciclo 2n−k-(real)) es una combinación perfecta.

La dualidad de Poincaré también invierte dimensiones; corresponde al hecho de que, si una variedad topológica se representa como un complejo de celdas, entonces el dual del complejo (una generalización de dimensiones superiores del gráfico dual plano) representa la misma variedad. En la dualidad de Poincaré, este homeomorfismo se refleja en un isomorfismo del késimo grupo de homología y el (n − k)ésimo grupo de cohomología.

Dualidad en geometría algebraica y aritmética

El mismo patrón de dualidad se aplica a una variedad proyectiva suave sobre un campo separablemente cerrado, utilizando en su lugar cohomología l-ádica con coeficientes Q_ℓ. Esto se generaliza aún más a variedades posiblemente singulares, utilizando en su lugar la cohomología de intersección, una dualidad llamada dualidad de Verdier. La dualidad de Serre o la dualidad coherente son similares a las afirmaciones anteriores, pero se aplican a la cohomología de haces coherentes.

Resulta que a medida que aumenta el nivel de generalidad, una cantidad cada vez mayor de conocimientos técnicos es útil o necesaria para comprender estos teoremas: la formulación moderna de estas dualidades se puede realizar utilizando categorías derivadas y ciertos funtores de imagen directos e inversos de haces (con respecto a la topología analítica clásica sobre variedades para la dualidad de Poincaré, las gavillas l-ádicas y la topología étale en el segundo caso, y con respecto a las gavillas coherentes para la dualidad coherente).

Otro grupo de declaraciones de dualidad similares se encuentra en aritmética: étale cohomology of finite, local and global fields (también conocido como cohomology de Galois, ya que étale cohomology over a field es equivalente a cohomology de grupo del (absoluto) Grupo Galois del campo) admite pares similares. El grupo absoluto Galois G()F_q) de un campo finito, por ejemplo, es isomorfo a ${displaystyle {widehat {mathbf {Z}}$ , la terminación definitiva de Z, los enteros. Por lo tanto, el emparejado perfecto (para cualquier G-module M)

Hⁿ()G, M) × H^{1 - 1n} ()G, HomM, Q/Z) → Q/Z

es una consecuencia directa de la dualidad de Pontryagin de grupos finitos. Para los campos local y global, existen afirmaciones similares (dualidad local y dualidad global o Poitou-Tate).

Contenido relacionado

Más resultados...