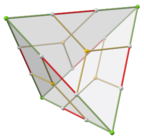
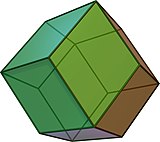
Dodecaedro
En geometría, un dodecaedro (griego δωδεκάεδρον, de δώδεκα dōdeka "doce" + ἕδρα hédra "base", "asiento" o "cara") o duodecaedro es cualquier poliedro de doce caras planas. El dodecaedro más familiar es el dodecaedro regular con pentágonos regulares como caras, que es un sólido platónico. También hay tres dodecaedros de estrellas regulares, que se construyen como estelaciones de forma convexa. Todos estos tienen simetría icosaédrica, orden 120.
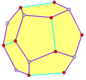
Algunos dodecaedros tienen la misma estructura combinatoria que el dodecaedro regular (en cuanto al grafo formado por sus vértices y aristas), pero sus caras pentagonales no son regulares: El piritoedro, una forma cristalina común en la pirita, tiene simetría piritoédrica, mientras que el tetartoide tiene simetría tetraédrica.
El dodecaedro rómbico puede verse como un caso límite del piritoedro y tiene simetría octaédrica. Las variaciones del dodecaedro alargado y el dodecaedro trapezo-rómbico, junto con el dodecaedro rómbico, llenan el espacio. Hay muchos otros dodecaedros.
Si bien el dodecaedro regular comparte muchas características con otros sólidos platónicos, una propiedad única es que se puede comenzar en una esquina de la superficie y dibujar un número infinito de líneas rectas a lo largo de la figura que regresan al punto original sin cruzarse. sobre cualquier otra esquina.
Dodecaedro regular
El dodecaedro regular convexo es uno de los cinco sólidos platónicos regulares y se puede representar con su símbolo de Schläfli {5, 3}.
El poliedro dual es el icosaedro regular {3, 5}, que tiene cinco triángulos equiláteros alrededor de cada vértice.
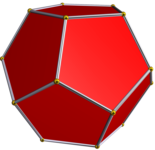 Convex regular dodecahedron |  Pequeño dodecaedro estelar |  Gran dodecahedron |  Gran dodecaedro estelar |
El dodecaedro regular convexo también tiene tres estelaciones, todas las cuales son dodecaedros regulares de estrella. Forman tres de los cuatro poliedros de Kepler-Poinsot. Son el pequeño dodecaedro estrellado {5/2, 5}, el gran dodecaedro {5, 5/2} y el gran dodecaedro estrellado {5/2, 3}. El pequeño dodecaedro estrellado y el gran dodecaedro son duales entre sí; el gran dodecaedro estrellado es dual al gran icosaedro {3, 5/2}. Todos estos dodecaedros estrella regulares tienen caras pentagonales o pentagrammicas regulares. El dodecaedro regular convexo y el gran dodecaedro estrellado son realizaciones diferentes del mismo poliedro regular abstracto; el pequeño dodecaedro estrellado y el gran dodecaedro son realizaciones diferentes de otro poliedro regular abstracto.
Otros dodecaedros pentagonales
En cristalografía, dos dodecaedros importantes pueden presentarse como formas cristalinas en algunas clases de simetría del sistema cristalino cúbico que son topológicamente equivalentes al dodecaedro regular pero menos simétricos: el piritoedro con simetría piritoédrica y el tetartoide con simetría tetraédrica:
Piritoedro
Un piritoedro es un dodecaedro con simetría piritoédrica (Th). Al igual que el dodecaedro regular, tiene doce caras pentagonales idénticas, tres de las cuales se encuentran en cada uno de los 20 vértices (ver figura). Sin embargo, los pentágonos no están obligados a ser regulares y la disposición atómica subyacente no tiene un verdadero eje de simetría quíntuple. Sus 30 aristas se dividen en dos conjuntos, que contienen 24 y 6 aristas de la misma longitud. Los únicos ejes de simetría rotacional son tres ejes dobles mutuamente perpendiculares y cuatro ejes triples.
Aunque los dodecaedros regulares no existen en los cristales, la forma de piritoedro se presenta en los cristales del mineral pirita, y puede ser una inspiración para el descubrimiento de la forma sólida platónica regular. El verdadero dodecaedro regular puede presentarse como una forma de cuasicristales (como el cuasicristal de holmio-magnesio-zinc) con simetría icosaédrica, que incluye verdaderos ejes de rotación quíntuple.
Pirita de cristal
El nombre pirita cristalina proviene de uno de los dos hábitos cristalinos comunes que muestra la pirita (el otro es el cubo). En la pirita piritoédrica, las caras tienen un índice de Miller de (210), lo que significa que el ángulo diedro es 2·arctan(2) ≈ 126,87° y cada cara pentagonal tiene un ángulo de aproximadamente 121,6° entre dos ángulos de aproximadamente 106,6° y dos ángulos opuestos de aproximadamente 102,6°. Las siguientes fórmulas muestran las medidas de la cara de un cristal perfecto (que rara vez se encuentra en la naturaleza).
Altura=52⋅ ⋅ Largo lado{displaystyle {text{}}={frac} {sqrt {5} {cdot {text{Long side}}} {cdot {cdot {f}} {cdot {f}} {cdot {fnK}}}}}} {cdot {cdot {cdot {cdot {cdot {f}}}}}}}}}} {cdot {cdot {cdot {cdot {cdot}}}}}}}}}}}}}}}} {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {cdot {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
Width=43⋅ ⋅ Largo lado{displaystyle {text{Width}={frac} {4}{3}cdot {text{Long side}}
Lados cortos=712⋅ ⋅ Largo lado{displaystyle {text{Short sides}}={sqrt {frac}}cdot {text{Long side}}}}
Pirita natural (con ángulos de cara a la derecha) |
Coordenadas cartesianas
Los ocho vértices de un cubo tienen las coordenadas (±1, ±1, ±1).
Las coordenadas de los 12 vértices adicionales son (0, ±(1 + h), ±(1 − h2)), (±(1 + h), ±(1 − h2), 0) y (±(1 − h2), 0, ±(1 + h)).
h es la altura del "techo" en forma de cuña; sobre las caras de ese cubo con longitud de arista 2.
Un caso importante es h = 1/2 (un cuarto de la longitud de la arista del cubo) para una pirita natural perfecta (también el piritoedro en la estructura de Weaire-Phelan).
Otro es h = 1/φ = 0,618... para el dodecaedro regular. Ver apartado Libertad geométrica para otros casos.
Dos piritoedros con coordenadas distintas de cero intercambiadas están en posiciones duales entre sí como el dodecaedro en el compuesto de dos dodecaedros.
Proyecciones ortoográficas del piritoedro con h = 1/2 | Heights 1/2 y 1/φ |
| Animaciones | |
|---|---|
 |  |
| Honeycomb de convex alternante y concave pyritohedra con alturas entre ±1/φ | Alturas entre 0 (cubo) y 1 (dodecahedro róbico) |
Libertad geométrica
El piritoedro tiene un grado geométrico de libertad con casos límite de un casco cúbico convexo en un límite de aristas colineales, y un dodecaedro rómbico como el otro límite cuando 6 aristas se degeneran a longitud cero. El dodecaedro regular representa un caso intermedio especial donde todas las aristas y ángulos son iguales.
Es posible superar estos casos límite, creando piritoedros cóncavos o no convexos. El endo-dodecaedro es cóncavo y equilátero; puede teselar el espacio con el dodecaedro regular convexo. Continuando desde allí en esa dirección, pasamos a través de un caso degenerado donde doce vértices coinciden en el centro, y al gran dodecaedro estrellado regular donde todas las aristas y ángulos son iguales de nuevo, y las caras se han distorsionado en pentagramas regulares. Por otro lado, más allá del dodecaedro rómbico, obtenemos un dodecaedro equilátero no convexo con caras pentagonales equiláteras en forma de pez que se cortan a sí mismas.
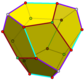
Tetartoide
Un tetartoide (también dodecaedro pentagonal tetragonal, pentágono-tritetraedro y dodecaedro pentágono tetraédrico) es un dodecaedro con simetría tetraédrica quiral (T). Al igual que el dodecaedro regular, tiene doce caras pentagonales idénticas, tres de las cuales se encuentran en cada uno de los 20 vértices. Sin embargo, los pentágonos no son regulares y la figura no tiene ejes de simetría quíntuple.
Aunque los dodecaedros regulares no existen en los cristales, sí existe la forma tetartoidea. El nombre tetartoide proviene de la raíz griega de un cuarto porque tiene un cuarto de simetría octaédrica completa y la mitad de simetría piritoédrica. El mineral cobaltita puede tener esta forma de simetría.
Se pueden crear abstracciones que comparten la topología y la simetría del sólido a partir del cubo y el tetraedro. En el cubo, cada cara está dividida en dos por un borde inclinado. En el tetraedro, cada arista se triseca y cada uno de los nuevos vértices se conecta a un centro de cara. (En la notación de poliedro de Conway, este es un tetraedro giroscópico).
Proyecciones ortoográficas de ejes 2 y 3 veces | Forma cúbica y tetraedral |
| Relación con los diakis dodecahedron | ||
|---|---|---|
Un tetartoide se puede crear al ampliar 12 de las 24 caras de un dodecaedro de los diakis. (El tetartoide que se muestra aquí se basa en uno que se crea por sí mismo al agrandar 24 de las 48 caras de los disdyakis dodecahedron.)
El modelo de cristal de la derecha muestra un tetartoide creado al agrandar las caras azules del núcleo dodecaedral de los diakis. Por lo tanto, los bordes entre las caras azules están cubiertos por los bordes de esqueleto rojo. |
Coordenadas cartesianas
Los siguientes puntos son vértices de un pentágono tetartoideo bajo simetría tetraédrica:
- ()a, b, c);a, −b, c);n/d1, −n/d1, n/d1);c, −a, b);n/d2, n/d2, n/d2),
bajo las siguientes condiciones:
- 0 ≤ a ≤ b ≤ c,
- n = a2c − bc2,
- d1 = a2 − ab + b2 + ac − 2bc,
- d2 = a2 + ab + b2 − ac − 2bc,
- nd1d2 ل 0.
Libertad geométrica
El dodecaedro regular es un tetartoide con más de la simetría requerida. El tetraedro triakis es un caso degenerado con 12 aristas de longitud cero. (En términos de los colores utilizados anteriormente, esto significa que los vértices blancos y los bordes verdes son absorbidos por los vértices verdes).
| Variaciones tetartoideas de dodecaedro regular a triakis tetrahedron | |||||||
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |
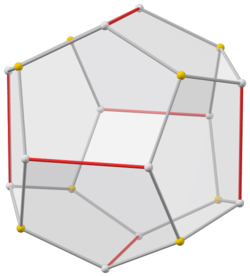
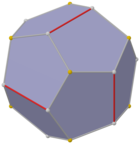
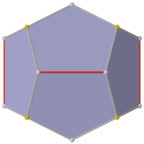
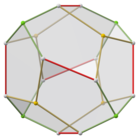
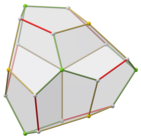
Doble de girobiánticúpula triangular
Se puede construir una forma de simetría inferior del dodecaedro regular como el dual de un poliedro construido a partir de dos anticúpulas triangulares conectadas de base a base, llamada girobianticúpula triangular. Tiene D Simetría 3d, orden 12. Tiene 2 conjuntos de 3 pentágonos idénticos en la parte superior e inferior, conectados 6 pentágonos alrededor de los lados que se alternan hacia arriba y hacia abajo. Esta forma tiene una sección transversal hexagonal y se pueden conectar copias idénticas como un panal hexagonal parcial, pero no todos los vértices coincidirán.
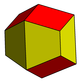
Dodecaedro rómbico
El dodecaedro rómbico es un zonoedro con doce caras rómbicas y simetría octaédrica. Es dual al cuboctaedro casi regular (un sólido de Arquímedes) y se presenta en la naturaleza en forma de cristal. El dodecaedro rómbico se empaqueta para llenar el espacio.
El dodecaedro rómbico puede verse como un piritoedro degenerado donde las 6 aristas especiales se han reducido a cero, reduciendo los pentágonos a caras rómbicas.
El dodecaedro rómbico tiene varias estelaciones, la primera de las cuales también es un relleno de espacio paraleloédrico.
Otro dodecaedro rómbico importante, el dodecaedro de Bilinski, tiene doce caras congruentes con las del triacontaedro rómbico, es decir, las diagonales están en la proporción de la proporción áurea. También es un zonoedro y fue descrito por Bilinski en 1960. Esta figura es otro relleno de espacio y también puede ocurrir en rellenos de espacio no periódicos junto con el triacontaedro rómbico, el icosaedro rómbico y el hexaedro rómbico.
Otros dodecaedros
Hay 6 384 634 dodecaedros convexos topológicamente distintos, excluyendo imágenes especulares: el número de vértices varía de 8 a 20. (Dos poliedros son "topológicamente distintos" si tienen intrínsecamente diferentes arreglos de caras y vértices, de modo que es imposible distorsionar uno en el otro simplemente cambiando las longitudes de los bordes o los ángulos entre los bordes o las caras).
Dodecaedros topológicamente distintos (excluyendo formas pentagonales y rómbicas)
- Uniform polyhedra:
- Prisma Decagonal – 10 plazas, 2 decagones, simetría D10h, orden 40.
- Antiprisma pentagonal – 10 triángulos equiláteros, 2 pentágonos, simetría D5d, orden 20
- sólidos Johnson (frente regular):
- Cupola pentagonal – 5 triángulos, 5 cuadrados, 1 pentágono, 1 decagon, simetría C5v, orden 10
- Snub disphenoid – 12 triángulos, D2d, orden 8
- Dipyramid cuadrado alargado – 8 triángulos y 4 cuadrados, simetría D4h, orden 16
- Metabidiminished icosahedron – 10 triángulos y 2 pentágonos, simetría C2v, orden 4
- Congruente irregular enfrentado: (facio-transitivo)
- Bipirámide hexagonal – 12 triángulos isosceles, doble de prisma hexagonal, simetría D6h, orden 24
- Trampezohedro hexagonal – 12 kites, doble antiprismo hexagonal, simetría D6d, orden 24
- Triakis tetraedro – 12 triángulos isosceles, doble de tetraedro truncado, Simetría Td, orden 24
- Other less regular faced:
- pirámide hendecagonal – 11 triángulos isosceles y 1 hendecagon regular, C11v, orden 11
- Trapezo-rhombic dodecahedron – 6 rhombi, 6 trapezoids – dual of triangular orthobicupola, simetría D3h, orden 12
- Rhombo-hexagonal dodecahedron o elongated Dodecahedron – 8 rhombi y 4 hexágonos equiláteros, simetría D4h, orden 16
- Truncated pentagonal trapezohedron, D5d, order 20, topologically equivalent to regular dodecahedron
Uso práctico
Armand Spitz usó un dodecaedro como el "globo" equivalente para su proyector de planetario Digital Dome. basado en una sugerencia de Albert Einstein.
Contenido relacionado
Elipsoide
Triple pitagórico
Los problemas de Hilbert