Distribución de Pareto

La distribución de Pareto, llamada así por el ingeniero civil, economista y sociólogo italiano Vilfredo Pareto (italiano: [paˈreːto] pə-RAY-toh), es una distribución de probabilidad de ley de potencia que se utiliza en la descripción de control social, de calidad, científico, geofísico, actuarial, y muchos otros tipos de fenómenos observables; el principio se aplicó originalmente para describir la distribución de la riqueza en una sociedad, y se ajusta a la tendencia de que una gran parte de la riqueza está en manos de una pequeña fracción de la población. El principio de Pareto o "regla 80-20" afirmar que el 80 % de los resultados se deben al 20 % de las causas se nombró en honor a Pareto, pero los conceptos son distintos y solo las distribuciones de Pareto con valor de forma (α ) de log₄5 ≈ 1.16 lo refleja con precisión. La observación empírica ha demostrado que esta distribución 80-20 se ajusta a una amplia gama de casos, incluidos los fenómenos naturales y las actividades humanas.

Definiciones

Si X es una variable aleatoria con una distribución de Pareto (Tipo I), entonces la probabilidad de que X sea mayor que algún número x, es decir, la función de supervivencia (también llamada función de cola), viene dada por

x)={begin{cases}left({frac {x_{mathrm {m} }}{x}}right)^{alpha }&xgeq x_{mathrm {m} },\1&xF̄ ̄ ()x)=Pr()X■x)={}()xmx)α α x≥ ≥ xm,1x.xm,{displaystyle {overline {F}(x)=Pr(X títulox)={begin{cases}left({frac] {x_{mathrm} {x}}right)}{alpha } {xgeq x_{mathrm {m},1 }1 golpex 0mathrm {m},end{cases}}}}}}}}} {cH00}}} {cH00}}} {cH00}}}}}}}}}}}}}}} {m}}}}} {m} {m}}}}}}}}}}} {m}}}}}}} {m}}}} {m}}}}} {m}}}}}}}}}}}}}}}}} {m} {m}}}}}} {m} {m}}}}} {m}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}x)={begin{cases}left({frac {x_{mathrm {m} }}{x}}right)^{alpha }&xgeq x_{mathrm {m} },\1&x

donde x_m es el valor mínimo posible (necesariamente positivo) de X, y α es un parámetro positivo. La distribución de Pareto Tipo I se caracteriza por un parámetro de escala x_m y un parámetro de forma α, que se conoce como el índice de cola . Cuando esta distribución se utiliza para modelar la distribución de la riqueza, el parámetro α se denomina índice de Pareto.

Función de distribución acumulativa

De la definición, la función de distribución acumulada de una variable aleatoria de Pareto con parámetros α y x_m es

<math alttext="{displaystyle F_{X}(x)={begin{cases}1-left({frac {x_{mathrm {m} }}{x}}right)^{alpha }&xgeq x_{mathrm {m} },\0&xFX()x)={}1− − ()xmx)α α x≥ ≥ xm,0x.xm.{displaystyle F_{X}(x)={begin{cases}1-left({frac {x_{mathrm {m}} {x}}derecha)}{alpha } diezxgeq x_{mathrm {m}, Umx secnx_{mathrm}.end{cases}}}<img alt="F_X(x) = begin{cases} 1-left(frac{x_mathrm{m}}{x}right)^alpha & x ge x_mathrm{m}, \ 0 & x

Función de densidad de probabilidad

Se sigue (por diferenciación) que la función de densidad de probabilidad es

<math alttext="{displaystyle f_{X}(x)={begin{cases}{frac {alpha x_{mathrm {m} }^{alpha }}{x^{alpha +1}}}&xgeq x_{mathrm {m} },\0&xfX()x)={}α α xmα α xα α +1x≥ ≥ xm,0x.xm.{displaystyle f_{X}(x)={begin{cases}{frac {alpha x_{mathrm {m} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} }{x^{alpha {fnMicrosoft Sans Serif}<img alt="f_X(x)= begin{cases} frac{alpha x_mathrm{m}^alpha}{x^{alpha+1}} & x ge x_mathrm{m}, \ 0 & x

Cuando se traza en ejes lineales, la distribución asume la familiar curva en forma de J que se aproxima asintóticamente a cada uno de los ejes ortogonales. Todos los segmentos de la curva son autosimilares (sujetos a factores de escala apropiados). Cuando se traza en un gráfico logarítmico, la distribución se representa mediante una línea recta.

Propiedades

Momentos y función característica

• El valor esperado de una variable aleatoria tras una distribución de Pareto es

1.end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">E⁡ ⁡ ()X)={}JUEGO JUEGO α α ≤ ≤ 1,α α xmα α − − 1α α ■1.{displaystyle operatorname {E} (X)={begin{cases}infty &alpha leq 1,{frac {alpha x_{mathrm {m} {alpha -1} {alpha }end{cases}}1.end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/231bd7e111557666fc015df16ff19e4686073368" style="vertical-align: -2.671ex; width:23.787ex; height:6.509ex;"/>

• La diferencia de una variable aleatoria tras una distribución de Pareto es

2.end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">Var⁡ ⁡ ()X)={}JUEGO JUEGO α α ▪ ▪ ()1,2],()xmα α − − 1)2α α α α − − 2α α ■2.{displaystyle operatorname {Var} (X)={begin{cases}infty &alpha in (1,2],\\left({frac {x_{mathrm {m}{alpha -1}right)}{2}{frac}{frac}{frac}} {m} {fnMicroc}}}}}}}} {f}}}}}}}{f}}}}{f}}}}}}}}}}{f}}}}}}}}}{f}{m}{f}}}{f}}}}}}}{f}}}{f}{f}} {f}} {f}}}}}}}}}}{f}}}}}}}}}}}}}}}}}}}}}}}{f}}}}}}}}}}}}}{m} {f}}}}}} {alpha }{alpha -2} {alpha }} {end{cases}}}2.end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bda6ae1a69ab2c130545abd2053226a4d6510558" style="vertical-align: -3.505ex; width:37.344ex; height:8.176ex;"/>

(Si) α ≤ 1, la diferencia no existe.)

• Los momentos crudos son

n.end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">μ μ n.={}JUEGO JUEGO α α ≤ ≤ n,α α xmnα α − − nα α ■n.{displaystyle mu _{n}'={begin{cases}infty &alpha leq n,\{frac {alpha x_{mathrm {m}{n}{n}{alpha - ¿Qué?n. end{cases}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/950b5c45974152256f828be1bd1911d187e50fa8" style="vertical-align: -3.171ex; width:21.446ex; height:7.509ex;"/>

• La función generadora de momento solo se define para valores no positivos t≤ 0

M()t;α α ,xm)=E⁡ ⁡ [etX]=α α ()− − xmt)α α .. ()− − α α ,− − xmt){displaystyle Mleft(t;alphax_{mathrm {m}right)=operatorname {E} left[e^{tX}right]=alpha (-x_{mathrm {m} }t)^{alpha }Gamma (-alpha-x_{mathrm {m}t)}}}}}

M()0,α α ,xm)=1.{displaystyle Mleft(0,alphax_{mathrm {m}right)=1.}

Así pues, puesto que la expectativa no converge en un intervalo abierto que contiene t=0{displaystyle t=0} decimos que la función generadora del momento no existe.

• La función característica es dada por

φ φ ()t;α α ,xm)=α α ()− − ixmt)α α .. ()− − α α ,− − ixmt),{displaystyle varphi (t;alphax_{mathrm {m})=alpha (-ix_{mathrm {m}t)^{alpha }Gamma (-alpha-ix_{mathrm {m}t),}}}}}}

Dondea,x) es la función gamma incompleta.

Los parámetros pueden resolverse utilizando el método de los momentos.

Distribuciones condicionales

La distribución condicional de probabilidad de una variable aleatoria distribuida por Pareto, dado que es mayor o igual a un número determinadox1{displaystyle x_{1}} en exceso xm{displaystyle x_{text{m}}, es una distribución de Pareto con el mismo índice de Paretoα α {displaystyle alpha } pero con mínimox1{displaystyle x_{1}} en lugar de xm{displaystyle x_{text{m}}. Esto implica que el valor esperado condicional (si es finito, es decir. 1}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■1{displaystyle alpha }1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/17d81dbbc4786493c7b8548cc324a978d7cf5dbd" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/>) es proporcional a x1{displaystyle x_{1}}. En caso de variables aleatorias que describen la vida de un objeto, esto significa que la esperanza de vida es proporcional a la edad, y se llama el efecto Lindy o la Ley de Lindy.

Un teorema de caracterización

Suppose X1,X2,X3,...... {displaystyle X_{1},X_{2},X_{3},dotsc son independientes idénticamente distribuidas variables aleatorias cuya distribución de probabilidad se soporta en el intervalo [xm,JUEGO JUEGO ){displaystyle [x_{text{m}},infty)} para algunos 0}" xmlns="http://www.w3.org/1998/Math/MathML">xm■0{displaystyle x_{text{m} {f}}} {fnMicrosoft}}}}} {fnK}}}}}}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4d17f55b7a3113b04a88d752f00ca2b88cd38a" style="vertical-align: -0.671ex; width:7.192ex; height:2.509ex;"/>. Supongamos eso para todos n{displaystyle n}, las dos variables aleatorias min{}X1,...... ,Xn}{displaystyle min{X_{1},dotscX_{n}}} y ()X1+⋯ ⋯ +Xn)/min{}X1,...... ,Xn}{displaystyle (X_{1}+dotsb +X_{n}/min{X_{1},dotscX_{n}}} son independientes. Entonces la distribución común es una distribución de Pareto.

Media geométrica

La media geométrica (G) es

G=xmexp⁡ ⁡ ()1α α ).{displaystyle G=x_{text{m}exp left({frac {1}{alpha }right). }

Media armónica

La media armónica (H) es

H=xm()1+1α α ).{displaystyle H=x_{text{m}left(1+{frac {1}{alpha }right). }

Representación gráfica

La característica curva 'cola larga' distribución cuando se traza en una escala lineal, enmascara la simplicidad subyacente de la función cuando se traza en un gráfico logarítmico, que luego toma la forma de una línea recta con gradiente negativo: De la fórmula para la función de densidad de probabilidad se deduce que para x ≥ x_m,

log⁡ ⁡ fX()x)=log⁡ ⁡ ()α α xmα α xα α +1)=log⁡ ⁡ ()α α xmα α )− − ()α α +1)log⁡ ⁡ x.{displaystyle log f_{X}(x)=log left(alpha {frac {x_{mathrm {m} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {x}{alpha +1}}right)=log(alpha x_{mathrm {m} {alpha })-(alpha +1)log x.}

Dado que α es positivo, el gradiente −(α + 1) es negativo.

Distribuciones relacionadas

Distribuciones de Pareto generalizadas

Existe una jerarquía de distribuciones de Pareto conocida como distribuciones de Pareto Tipo I, II, III, IV y Feller-Pareto. Pareto Tipo IV contiene Pareto Tipo I-III como casos especiales. La distribución Feller-Pareto generaliza el Tipo IV de Pareto.

Tipos de Pareto I–IV

La jerarquía de distribución de Pareto se resume en la siguiente tabla comparando las funciones de supervivencia (CDF complementaria).

Cuando μ = 0, la distribución de Pareto Tipo II también se conoce como distribución Lomax.

En esta sección, el símbolo x_m, utilizado anteriormente para indicar el valor mínimo de x, se sustituye por σ .

Distribución de los padres

	F̄ ̄ ()x)=1− − F()x){displaystyle {overline {F}(x)=1-F(x)}	Apoyo	Parámetros
Tipo I	[xσ σ ]− − α α {displaystyle left[{frac {x}{sigma Bien.	x≥ ≥ σ σ {displaystyle xgeq sigma }	0,alpha }" xmlns="http://www.w3.org/1998/Math/MathML">σ σ ■0,α α {displaystyle sigma >0,alpha } 0, alpha" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/754f7860537646aecb5a1dd34fd99dfb792c98ed" style="vertical-align: -0.671ex; width:8.112ex; height:2.509ex;"/>
Tipo II	[1+x− − μ μ σ σ ]− − α α {displaystyle left[1+{frac {x-mu }{sigma }right]^{-alpha }}	x≥ ≥ μ μ {displaystyle xgeqmu}	0,alpha }" xmlns="http://www.w3.org/1998/Math/MathML">μ μ ▪ ▪ R,σ σ ■0,α α {displaystyle mu in mathbb {R}sigma œ0,alpha } 0, alpha" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/40d133c8542cb10d35880958772047afe9e286c2" style="vertical-align: -0.838ex; width:15.067ex; height:2.676ex;"/>
Lomax	[1+xσ σ ]− − α α {displaystyle left[1+{frac {x}{sigma Bien.	x≥ ≥ 0{displaystyle xgeq 0}	0,alpha }" xmlns="http://www.w3.org/1998/Math/MathML">σ σ ■0,α α {displaystyle sigma >0,alpha } 0, alpha" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/754f7860537646aecb5a1dd34fd99dfb792c98ed" style="vertical-align: -0.671ex; width:8.112ex; height:2.509ex;"/>
Tipo III	[1+()x− − μ μ σ σ )1/γ γ ]− − 1{displaystyle left[1+left({frac {x-mu }{sigma }right)^{1/gamma - Sí.	x≥ ≥ μ μ {displaystyle xgeqmu}	0}" xmlns="http://www.w3.org/1998/Math/MathML">μ μ ▪ ▪ R,σ σ ,γ γ ■0{displaystyle mu in mathbb {R}sigmagamma } 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbf5d82227cde44d7f9244c41e02971516e1be0" style="vertical-align: -0.838ex; width:14.841ex; height:2.676ex;"/>
Tipo IV	[1+()x− − μ μ σ σ )1/γ γ ]− − α α {displaystyle left[1+left({frac {x-mu }{sigma }right)^{1/gamma }right]^{-alpha }}}	x≥ ≥ μ μ {displaystyle xgeqmu}	0,alpha }" xmlns="http://www.w3.org/1998/Math/MathML">μ μ ▪ ▪ R,σ σ ,γ γ ■0,α α {displaystyle mu in mathbb {R}sigmagamma } 0, alpha" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/10e6c204db2658745897265a373f0dac44364442" style="vertical-align: -0.838ex; width:17.363ex; height:2.676ex;"/>

El parámetro de forma α es el índice de la cola, μ es la ubicación, σ es la escala, γ es un parámetro de desigualdad. Algunos casos especiales de Pareto Tipo (IV) son

P()IV)()σ σ ,σ σ ,1,α α )=P()I)()σ σ ,α α ),{displaystyle P(IV)(sigmasigma1,alpha)=P(I)(sigmaalpha),}

P()IV)()μ μ ,σ σ ,1,α α )=P()II)()μ μ ,σ σ ,α α ),{displaystyle P(IV)(musigma1,alpha)=P(II)(musigmaalpha),}

P()IV)()μ μ ,σ σ ,γ γ ,1)=P()III)()μ μ ,σ σ ,γ γ ).{displaystyle P(IV)(musigmagamma1)=P(III)(musigmagamma). }

La finitud de la media, y la existencia y la finitud de la varianza dependen del índice de cola α (índice de desigualdad γ). En particular, los δ-momentos fraccionarios son finitos para algunos δ > 0, como se muestra en la siguiente tabla, donde δ no es necesariamente un número entero.

Momentos de distribución Pareto I–IV (caso μ = 0)

	E⁡ ⁡ [X]{displaystyle operatorname {E} [X]}	Estado	E⁡ ⁡ [Xδ δ ]{displaystyle operatorname [X^{delta]	Estado
Tipo I	σ σ α α α α − − 1{displaystyle {frac {sigma alpha ♫{alpha - Sí.	1}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■1{displaystyle alpha }1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/17d81dbbc4786493c7b8548cc324a978d7cf5dbd" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/>	σ σ δ δ α α α α − − δ δ {displaystyle {frac {sigma }{delta Alpha -delta }	<math alttext="{displaystyle delta δ δ .α α {displaystyle delta]<img alt=" delta
Tipo II	σ σ α α − − 1+μ μ {displaystyle {frac {sigma ♫{alpha - ¿Qué?	1}" xmlns="http://www.w3.org/1998/Math/MathML">α α ■1{displaystyle alpha }1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/17d81dbbc4786493c7b8548cc324a978d7cf5dbd" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/>	σ σ δ δ .. ()α α − − δ δ ).. ()1+δ δ ).. ()α α ){displaystyle {frac {sigma }{delta }Gamma (alpha -delta)Gamma (1+delta)}{Gamma (alpha)}}}	<math alttext="{displaystyle 0<delta 0.δ δ .α α {displaystyle 0 madedelta<img alt="{displaystyle 0<delta
Tipo III	σ σ .. ()1− − γ γ ).. ()1+γ γ ){displaystyle sigma Gamma (1-gamma)Gamma (1+gamma)}	<math alttext="{displaystyle -1<gamma − − 1.γ γ .1{displaystyle -1 se hizo gamma.<img alt=" -1<gamma	σ σ δ δ .. ()1− − γ γ δ δ ).. ()1+γ γ δ δ ){displaystyle sigma ^{delta }Gamma (1-gamma delta)Gamma (1+gamma delta)}	<math alttext="{displaystyle -gamma ^{-1}<delta − − γ γ − − 1.δ δ .γ γ − − 1{displaystyle - ¿Qué? ♪♪gamma ^{-1}<img alt="-gamma^{-1}<delta
Tipo IV	σ σ .. ()α α − − γ γ ).. ()1+γ γ ).. ()α α ){displaystyle {frac {sigma Gamma (alpha -gamma)Gamma (1+gamma)}{Gamma (alpha)}}}}	<math alttext="{displaystyle -1<gamma − − 1.γ γ .α α {displaystyle -1 se hizo gamma<img alt=" -1<gamma	σ σ δ δ .. ()α α − − γ γ δ δ ).. ()1+γ γ δ δ ).. ()α α ){displaystyle {frac {sigma }{delta }Gamma (alpha -gamma delta)Gamma (1+gamma delta)}{Gamma (alpha)}}}}	<math alttext="{displaystyle -gamma ^{-1}<delta − − γ γ − − 1.δ δ .α α /γ γ {displaystyle - ¿Qué? # Imagino #<img alt="-gamma^{-1}<delta

Distribución Feller-Pareto

Feller define una variable de Pareto mediante la transformación U = Y⁻¹ − 1 de una variable aleatoria beta Y, cuya función de densidad de probabilidad es

<math alttext="{displaystyle f(y)={frac {y^{gamma _{1}-1}(1-y)^{gamma _{2}-1}}{B(gamma _{1},gamma _{2})}},qquad 0<y0,}" xmlns="http://www.w3.org/1998/Math/MathML">f()Sí.)=Sí.γ γ 1− − 1()1− − Sí.)γ γ 2− − 1B()γ γ 1,γ γ 2),0.Sí..1;γ γ 1,γ γ 2■0,{displaystyle f(y)={frac {y^{gamma ¿Por qué? {2}-1} {B(gamma _{1},gamma _{2}}}qquad 0 obtenidos1;gamma _{1},gamma ¿Qué?<img alt=" f(y) = frac{y^{gamma_1-1} (1-y)^{gamma_2-1}}{B(gamma_1, gamma_2)}, qquad 0<y0," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d70f10dfc751c4eee45d93dc34a2f1213a8fc8" style="vertical-align: -2.671ex; width:51.187ex; height:6.676ex;"/>

donde B() es la función beta. Si

0,gamma >0,}" xmlns="http://www.w3.org/1998/Math/MathML">W=μ μ +σ σ ()Y− − 1− − 1)γ γ ,σ σ ■0,γ γ ■0,{displaystyle W=mu +sigma (Y^{-1}-1)^{gamma },qquad sigma √0,gamma }0, gamma>0," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/69852671d4ccae45fdaf5dc49789e66493e400be" style="vertical-align: -0.838ex; width:40.749ex; height:3.176ex;"/>

entonces W tiene una distribución Feller-Pareto FP(μ, σ, γ, γ₁, γ₂).

Si U1♪ ♪ .. ()δ δ 1,1){displaystyle U_{1}sim Gamma (delta _{1},1)} y U2♪ ♪ .. ()δ δ 2,1){displaystyle U_{2}sim Gamma (delta _{2},1)} son variables independientes Gamma, otra construcción de una variable Feller-Pareto (FP) es

W=μ μ +σ σ ()U1U2)γ γ {displaystyle W=mu +sigma left({frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {dere}}}}}}}}}}}}}}} }

y escribimos W ~ FP(μ, σ, γ, δ₁, δ₂). Los casos especiales de la distribución de Feller-Pareto son

FP()σ σ ,σ σ ,1,1,α α )=P()I)()σ σ ,α α ){displaystyle FP(sigmasigma1,alpha)=P(I)(sigmaalpha)}

FP()μ μ ,σ σ ,1,1,α α )=P()II)()μ μ ,σ σ ,α α ){displaystyle FP(musigma1,alpha)=P(II)(musigmaalpha)}

FP()μ μ ,σ σ ,γ γ ,1,1)=P()III)()μ μ ,σ σ ,γ γ ){displaystyle FP(musigmagamma1,1)=P(III)(musigmagamma)}

FP()μ μ ,σ σ ,γ γ ,1,α α )=P()IV)()μ μ ,σ σ ,γ γ ,α α ).{displaystyle FP(musigmagamma1,alpha)=P(IV)(musigmagammaalpha). }

Distribución inversa de Pareto / Distribución de potencia

Cuando una variable aleatoria Y{displaystyle Sí. sigue una distribución pareto, luego su inverso X=1/Y{displaystyle X=1/Y} sigue una distribución Inverse Pareto. Distribución inversa de Pareto es equivalente a una distribución de Poder

<math alttext="{displaystyle Ysim mathrm {Pa} (alphax_{m})={frac {alpha x_{m}^{alpha }}{y^{alpha +1}}}quad (ygeq x_{m})quad Leftrightarrow quad Xsim mathrm {iPa} (alphax_{m})=mathrm {Power} (x_{m}^{-1},alpha)={frac {alpha x^{alpha -1}}{(x_{m}^{-1})^{alpha }}}quad (0Y♪ ♪ Pa()α α ,xm)=α α xmα α Sí.α α +1()Sí.≥ ≥ xm).. X♪ ♪ iPa()α α ,xm)=Power()xm− − 1,α α )=α α xα α − − 1()xm− − 1)α α ()0.x≤ ≤ xm− − 1){displaystyle Ysim mathrm {Pa} {alphax_{m}={frac {alpha x_{m}^{alpha }{y^{alpha #####}quad (ygeq x_{m})quad Leftrightarrow quad Xsim mathrm {iPa} (alphax_{m})=mathrm {Power} (x_{m}^{-1},alpha)={alpha x^{alpha - 1} {cHFF}}quad (0 secuestradoleq x_{m}}}}}}<img alt="{displaystyle Ysim mathrm {Pa} (alphax_{m})={frac {alpha x_{m}^{alpha }}{y^{alpha +1}}}quad (ygeq x_{m})quad Leftrightarrow quad Xsim mathrm {iPa} (alphax_{m})=mathrm {Power} (x_{m}^{-1},alpha)={frac {alpha x^{alpha -1}}{(x_{m}^{-1})^{alpha }}}quad (0

Relación con la distribución exponencial

La distribución de Pareto está relacionada con la distribución exponencial de la siguiente manera. Si X tiene una distribución de Pareto con x_m mínimos e índice α, entonces

Y=log⁡ ⁡ ()Xxm){displaystyle Y=log left({frac {X}{x_{mathrm {m}}right)}

se distribuye exponencialmente con el parámetro de tasa α. De manera equivalente, si Y se distribuye exponencialmente con tasa α, entonces

xmeY{displaystyle x_{mathrm}e^{Y}

tiene una distribución de Pareto con un mínimo de x_m y un índice α.

Esto se puede mostrar utilizando las técnicas estándar de cambio de variable:

<math alttext="{displaystyle {begin{aligned}Pr(Y<y)&=Pr left(log left({frac {X}{x_{mathrm {m} }}}right)<yright)\&=Pr(XPr()Y.Sí.)=Pr()log⁡ ⁡ ()Xxm).Sí.)=Pr()X.xmeSí.)=1− − ()xmxmeSí.)α α =1− − e− − α α Sí..{begin{aligned}Pr(Ycantay)}pr left(log left({frac {X}{x_{mathrm {m}}}}}}right) {derecho)derecho=pr(Xseq_{m} {m} {y} {m} {m} {m} {m} {ccccccccccccccccccccccccccc}ccccccccccccccccccccccccccccccccccccccccccccccccc {m}}{x_{mathrm Bien. }=1-e^{-alpha y}<img alt="{displaystyle {begin{aligned}Pr(Y<y)&=Pr left(log left({frac {X}{x_{mathrm {m} }}}right)<yright)\&=Pr(X

La última expresión es la función de distribución acumulativa de una distribución exponencial con tasa α.

La distribución de Pareto puede ser construida por distribuciones exponenciales jerárquicas. Vamos φ φ Silencioa♪ ♪ Gastos()a){fnMicrosoft Sans Serif}(a)} y .. Silencioφ φ ♪ ♪ Gastos()φ φ ){displaystyle eta Silenciophi sim {text{Exp}(phi)}. Entonces tenemos p().. Silencioa)=a()a+.. )2{fnMicrosoft Sans Serif}}} y, como resultado, a+.. ♪ ♪ Pareto()a,1){displaystyle a+eta sim {text{Pareto}(a,1)}.

Más en general, si λ λ ♪ ♪ Gamma()α α ,β β ){displaystyle lambda sim {text{Gamma}}(alphabeta)} (parametrización de tipos de formas) y .. Silencioλ λ ♪ ♪ Gastos()λ λ ){displaystyle eta tenciónlambda sim {text{Exp}(lambda)}, entonces β β +.. ♪ ♪ Pareto()β β ,α α ){displaystyle beta +eta sim {text{Pareto} {betaalpha)}.

Equivalentemente, si Y♪ ♪ Gamma()α α ,1){displaystyle Ysim {text{Gamma} {alpha1)} y X♪ ♪ Gastos()1){displaystyle Xsim {text{Exp}(1)}, entonces xm()1+XY)♪ ♪ Pareto()xm,α α ){displaystyle x_{text{m}!left(1+{frac} {X}{Y}right)sim {text{Pareto} {x_{text{m},alpha)}.

Relación con la distribución log-normal

La distribución de Pareto y la distribución log-normal son distribuciones alternativas para describir los mismos tipos de cantidades. Una de las conexiones entre los dos es que ambos son las distribuciones de la exponencial de las variables aleatorias distribuidas de acuerdo con otras distribuciones comunes, respectivamente, la distribución exponencial y la distribución normal. (Consulte la sección anterior).

Relación con la distribución de Pareto generalizada

La distribución de Pareto es un caso especial de la distribución de Pareto generalizada, que es una familia de distribuciones de forma similar, pero que contiene un parámetro adicional de tal manera que el soporte de la distribución está acotado por debajo (en un punto variable), o acotadas tanto por arriba como por abajo (donde ambas son variables), con la distribución Lomax como caso especial. Esta familia también contiene distribuciones exponenciales desplazadas y no desplazadas.

Distribución de Pareto con escala xm{displaystyle x_{m} y forma α α {displaystyle alpha } es equivalente a la distribución generalizada de Pareto con ubicación μ μ =xm{displaystyle mu =x_{m}, escala σ σ =xm/α α {displaystyle sigma =x_{m}/alpha } y forma .. =1/α α {displaystyle xi =1/alpha }. Vice versa uno puede conseguir la distribución de Pareto del GPD por xm=σ σ /.. {displaystyle x_{m}=sigma /xi } y α α =1/.. {displaystyle alpha =1/xi }.

Distribución de Pareto acotada

La distribución de Pareto acotada (o truncada) tiene tres parámetros: α, L y H. Como en la distribución estándar de Pareto α determina la forma. L indica el valor mínimo y H indica el valor máximo.

La función de densidad de probabilidad es

α α Lα α x− − α α − − 11− − ()LH)α α {fnMicroc {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ L^{alpha }x^{-alpha -1}{1-left({frac {H}right)}{alpha },

donde L ≤ x ≤ H, y α > 0.

Generación de variables aleatorias de Pareto acotadas

Si U se distribuye uniformemente en (0, 1), entonces se aplica el método de transformación inversa

U=1− − Lα α x− − α α 1− − ()LH)α α {displaystyle U={frac {1-L^{alpha }x^{-alpha }{1-({frac {L}{H} {fnMicrosoft Sans Serif} }

x=()− − UHα α − − ULα α − − Hα α Hα α Lα α )− − 1α α {displaystyle x=left(-{frac {UH^{alpha }-UL^{alpha }-H^{alpha {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {1}{alpha }

es una distribución de Pareto acotada.

Distribución simétrica de Pareto

El propósito de la distribución de Pareto simétrica y la distribución de Pareto simétrica cero es capturar alguna distribución estadística especial con un pico de probabilidad pronunciado y colas de probabilidad largas y simétricas. Estas dos distribuciones se derivan de la distribución de Pareto. La cola de probabilidad larga normalmente significa que la probabilidad decae lentamente. La distribución de Pareto realiza un trabajo de ajuste en muchos casos. Pero si la distribución tiene una estructura simétrica con dos colas que decaen lentamente, Pareto no podría hacerlo. Luego se aplica la distribución Pareto simétrico o Pareto simétrico cero.

La función de distribución acumulativa (CDF) de la distribución simétrica de Pareto se define de la siguiente manera:

<math alttext="{displaystyle F(X)=P(x<X)={begin{cases}{tfrac {1}{2}}({b over 2b-X})^{a}&XF()X)=P()x.X)={}12()b2b− − X)aX.b1− − 12()bX)aX≥ ≥ b{begin{cases}{tfrac {1}{b over 2b-X})} {{a} {1tfrac {2}{bover 2b-X})}{a} {1-{2}{tfrac {2} {tfrac {b}{X}}}}}} {a}}} {}}} {}} {}} {}}}} {}}}}}}} {}} {}}}}}}} {}} {}} {}}}}}}}} {} {}} {}}}} {}}}}} {}}}}}}}}}}}} {}}}}}}}}} {} {} {}}} {}}}}} {} {}}}}} {}}}}}}}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} { Xgeq bend{cases}}<img alt="{displaystyle F(X)=P(x<X)={begin{cases}{tfrac {1}{2}}({b over 2b-X})^{a}&X

La función de densidad de probabilidad correspondiente (PDF) es:

p()x)=aba2()b+Silenciox− − bSilencio)a+1,X▪ ▪ R{displaystyle p(x)={ab^{a} over 2(b+leftvert x-brightvert)^{a+1}, Xin R}

Esta distribución tiene dos parámetros: a y b. Es simétrica por b. Entonces la expectativa matemática es b. Cuando, tiene varianza de la siguiente manera:

E()()x− − b)2)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO ()x− − b)2p()x)dx=2b2()a− − 2)()a− − 1){displaystyle E(x-b)^{2})=int _{-infty }{infty }(x-b)^{2}p(x)dx={2b^{2} over (a-2)(a-1)}}

La distribución CDF de Zero Symmetric Pareto (ZSP) se define de la siguiente manera:

<math alttext="{displaystyle F(X)=P(x<X)={begin{cases}{tfrac {1}{2}}({b over b-X})^{a}&XF()X)=P()x.X)={}12()bb− − X)aX.01− − 12()bb+X)aX≥ ≥ 0{displaystyle F(X)=P(x obtenidosX)={begin{cases}{tfrac {1}{2} {b over b-X})^{a {01-{tfrac {1}{2} {tfrac {b}{b}{b+X}})} {a} {a} {a} {0g}}}}}}}}}}}}} {ccH00}} {c}}} {c}}}}}}}}}}} {ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc<img alt="{displaystyle F(X)=P(x<X)={begin{cases}{tfrac {1}{2}}({b over b-X})^{a}&X

El PDF correspondiente es:

p()x)=aba2()b+SilencioxSilencio)a+1,X▪ ▪ R{displaystyle p(x)={ab^{a} over 2(b+leftvert xrightvert)^{a+1}},Xin R}

Esta distribución es simétrica por cero. El parámetro a está relacionado con la tasa de disminución de la probabilidad y (a/2b) representa la magnitud máxima de la probabilidad.

Distribución de Pareto multivariada

La distribución de Pareto univariante se ha ampliado a una distribución de Pareto multivariante.

Inferencia estadística

Estimación de parámetros

La función de verosimilitud para los parámetros de distribución de Pareto α y x_m, dada una muestra independiente x = (x₁, x₂,..., x_n), es

L()α α ,xm)=∏ ∏ i=1nα α xmα α xiα α +1=α α nxmnα α ∏ ∏ i=1n1xiα α +1.{displaystyle L(alphax_{mathrm {m})=prod ##{i=1} {n}alpha {fnMicroc {x_{fnMicrom} {m} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnK}} {fnK}} {f}}} {f}}} {fn}} {fnK}}} {f}}} {f}}} {f}}}}} {f}}} {f}}}}}} {f}}}}}}} {f} {f}}}}}} {f} {f}}}}}}}}}}} {f} {f}} {f}}}} {f} {f}}}} {f}}}}} {f} {f} {f}} {f}}}}}}}}}} {f}}}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}} {f}}}}}}}}} ################################################################################################################################################################################################################################################################ ^{n}x_{mathrm {m} {nalpha }prod - ¿Qué? {1}{x_{i} {f} {f}} {f}} {f} {f}} {f} {f}} {f}}} {f}} {f}}} {f}} {f}}}} {f} {f}} {f}}}}}}} {f}}} {f}} {f}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}}}}} {f} {f} {f} {f}f}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f} {f} {f}}}f}}}}}}}}} #

Por lo tanto, la función de verosimilitud logarítmica es

l l ()α α ,xm)=nIn⁡ ⁡ α α +nα α In⁡ ⁡ xm− − ()α α +1).. i=1nIn⁡ ⁡ xi.{displaystyle ell (alphax_{mathrm {m})=nln alpha +nalpha ln x_{mathrm}-(alpha +1)sum ¿Por qué? x_{i}

Se puede ver que l l ()α α ,xm){displaystyle ell (alphax_{mathrm {m})} aumenta monotonicamente con x_m, es decir, cuanto mayor sea el valor x_m, cuanto mayor sea el valor de la función de probabilidad. Por lo tanto, desde x ≥ x_m, concluimos que

x^ ^ m=minixi.{displaystyle {widehat {x}_{mathrm} {m}=min ¿Qué?

Para encontrar el estimador de α, calculamos la derivada parcial correspondiente y determinamos dónde es cero:

∂ ∂ l l ∂ ∂ α α =nα α +nIn⁡ ⁡ xm− − .. i=1nIn⁡ ⁡ xi=0.{displaystyle {frac {partial ell }{partial alpha }={frac {n}{alpha }+nln x_{mathrm {m}-sum _{i=1} {n}ln} x_{i}=0.}

Por lo tanto, el estimador de máxima verosimilitud para α es:

α α ^ ^ =n.. iIn⁡ ⁡ ()xi/x^ ^ m).{displaystyle {widehat {alpha ¿Qué? (x_{i}/{widehat {x}_{mathrm {m}}}}}}

El error estadístico esperado es:

σ σ =α α ^ ^ n.{displaystyle sigma ={frac {widehat {Alpha}{sqrt {}}}}

Malik (1970) da la distribución conjunta exacta ()x^ ^ m,α α ^ ^ ){displaystyle ({hat {x}_{mathrm},{hat {alpha}}}}}}. En particular, x^ ^ m{displaystyle {hat {x}_{mathrm {m}}} {fn}} {fn}} {fn}}} y α α ^ ^ {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f} {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\fnMicrosoft {\\\\fnMicrosoft {\\\fn\\fnMicrosoft {fnMicrosoft {fnMicrosoft {\\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\\\\\fnMicrosoft {fnMicrosoft } son independientes x^ ^ m{displaystyle {hat {x}_{mathrm {m}}} {fn}} {fn}} {fn}}} es Pareto con parámetro escala x_m y parámetro de forma n, mientras α α ^ ^ {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {f} {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {f}fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\fnMicrosoft {\\\\fnMicrosoft {\\\fn\\fnMicrosoft {fnMicrosoft {fnMicrosoft {\\fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\\\\\\fnMicrosoft {fnMicrosoft } tiene una distribución inversa-gamma con parámetros de forma y escala n− 1 y n, respectivamente.

Ocurrencia y aplicaciones

Generales

Vilfredo Pareto usó originalmente esta distribución para describir la distribución de la riqueza entre los individuos, ya que parecía mostrar bastante bien la forma en que una porción más grande de la riqueza de cualquier sociedad es propiedad de un porcentaje más pequeño de personas en esa sociedad. También lo usó para describir la distribución del ingreso. Esta idea a veces se expresa más simplemente como el principio de Pareto o la 'regla 80-20'. que dice que el 20% de la población controla el 80% de la riqueza. Sin embargo, la regla 80-20 corresponde a un valor particular de α y, de hecho, los datos de Pareto sobre los impuestos sobre la renta británicos en su Cours d'économie politique indica que alrededor del 30% de la población tenía alrededor del 70% de los ingresos. El gráfico de la función de densidad de probabilidad (PDF) al principio de este artículo muestra que la "probabilidad" o fracción de la población que posee una pequeña cantidad de riqueza por persona es bastante alta y luego disminuye constantemente a medida que aumenta la riqueza. (Sin embargo, la distribución de Pareto no es realista para la riqueza del extremo inferior. De hecho, el valor neto puede incluso ser negativo). Esta distribución no se limita a describir la riqueza o el ingreso, sino a muchas situaciones en las que se encuentra un equilibrio en el distribución de la "pequeña" al "grande". Los siguientes ejemplos a veces se ven como aproximadamente distribuidos en Pareto:

• Los tamaños de los asentamientos humanos (pocas ciudades, muchos aldeanos/villagos)
• Distribución del tamaño de archivo del tráfico de Internet que utiliza el protocolo TCP (muchos archivos más pequeños, pocos más grandes)
• Tipos de error de disco duro
• Clusters de Bose–Einstein condensan cerca de cero absoluto

Distribución acumulada de Pareto (Lomax) a máximas precipitaciones de un día utilizando CumFreq, vea también ajuste de distribución

• Los valores de las reservas de petróleo en los campos petroleros (algunos campos grandes, muchos pequeños campos)
• La distribución de longitud en trabajos asignados a supercomputadores (unos pocos grandes, muchos pequeños)
• El precio estandarizado devuelve las acciones individuales
• Tamaños de partículas de arena
• El tamaño de los meteoritos
• Severity of large casualty losses for certain lines of business such as general liability, commercial auto, and workers compensation.
• Cantidad de tiempo un usuario en Steam pasará jugando diferentes juegos. (Algunos juegos se juegan mucho, pero la mayoría se juega casi nunca.) [2]
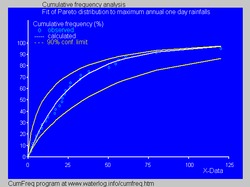
• En la hidrología, la distribución de Pareto se aplica a eventos extremos como precipitaciones máximas anuales de un día y descargas de ríos. El cuadro azul ilustra un ejemplo de equiparar la distribución de Pareto para clasificar anualmente las precipitaciones máximas de un día mostrando también el cinturón de confianza del 90% basado en la distribución binomio. Los datos de precipitaciones están representados por posiciones de trama como parte del análisis de frecuencia acumulativa.
• En Electric Utility Distribution Reliability (80% de las Minutes de Clientes Interrupted se producen aproximadamente el 20% de los días en un año determinado).

Relación con la ley de Zipf

La distribución de Pareto es una distribución continua de probabilidad. La ley de Zipf, también llamada la distribución de zeta, es una distribución discreta, separando los valores en un ranking simple. Ambos son una simple ley de poder con un exponente negativo, escalado para que sus distribuciones acumulativas sean iguales 1. El Zipf puede derivarse de la distribución de Pareto si x{displaystyle x} valores (ingresos) se vinculan N{displaystyle N} rangos para que el número de personas en cada bin siga un patrón de 1/rank. La distribución se normaliza definiendo xm{displaystyle x_{m} así α α xmα α =1H()N,α α − − 1){displaystyle alpha x_{mathrm {m} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} }={frac {1}{H(N,alpha -1)}}} Donde H()N,α α − − 1){displaystyle H(N,alpha -1)} es el número armónico generalizado. Esto hace que la función de densidad de probabilidad de Zipf se deriva de la de Pareto.

f()x)=α α xmα α xα α +1=1xsH()N,s){displaystyle f(x)={frac {alpha x_{mathrm {m} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} }{x^{alpha - Sí.

Donde s=α α − − 1{displaystyle s=alpha -1} y x{displaystyle x} es un número entero que representa el rango de 1 a N, donde N es el mayor rango de ingresos. Así que una persona seleccionada al azar (o palabra, enlace web o ciudad) de una población (o idioma, Internet o país) tiene f()x){displaystyle f(x)} probabilidad de clasificación x{displaystyle x}.

Relación con el "principio de Pareto"

La "ley 80-20", según la cual el 20% de todas las personas reciben el 80% de todos los ingresos, y el 20% del 20% más afluente recibe el 80% de ese 80%, y así sucesivamente, sostiene precisamente cuando el índice de Pareto es α α =log4⁡ ⁡ 5=log10⁡ ⁡ 5log10⁡ ⁡ 4.. 1.161{displaystyle alpha =log _{4}4}approx 1.161}. Este resultado puede derivarse de la fórmula curva Lorenz que se da a continuación. Además, se ha demostrado que los siguientes son matemáticamente equivalentes:

• Los ingresos se distribuyen según una distribución de Pareto con índice α■ 1.
• Hay un número 0 ≤p≤ 1/2 tal que 100p% de todas las personas reciben 100(1 −p)% de todos los ingresos, y de forma similar para cada real (no necesariamente entero) nØ 0, 100pⁿ% de todas las personas reciben 100(1 −p)ⁿ porcentaje de todos los ingresos. α y p relacionados por

1− − 1α α =In⁡ ⁡ ()1− − p)In⁡ ⁡ ()p)=In⁡ ⁡ ()()1− − p)n)In⁡ ⁡ ()pn){displaystyle 1-{frac}{alpha {fnK}} {fn}} {fnfn}}}}}}}} {fn}} {fn}} {fn}}}}}}}}} {ln}}}}} {fn}}}}}}

Esto no se aplica solo a los ingresos, sino también a la riqueza, oa cualquier otra cosa que pueda ser modelada por esta distribución.

Esto excluye las distribuciones de Pareto en las que 0 < α ≤ 1, que, como se señaló anteriormente, tienen un valor esperado infinito y, por lo tanto, no pueden modelar razonablemente la distribución del ingreso.

Relación con la ley de Price

La ley de raíz cuadrada de precio se ofrece a veces como una propiedad de o como similar a la distribución de Pareto. However, the law only holds in the case that α α =1{displaystyle alpha =1}. Tenga en cuenta que en este caso, la cantidad total y esperada de la riqueza no se define, y la regla sólo se aplica asintomáticamente a las muestras al azar. El principio ampliado de Pareto mencionado anteriormente es una regla mucho más general.

Curva de Lorenz y coeficiente de Gini

Curvas Lorenz para una serie de distribuciones de Pareto. El caso α= ∞ corresponde a una distribución perfectamente igual (G= 0) y el α= 1 línea corresponde a la desigualdad total (G= 1)

La curva de Lorenz se usa a menudo para caracterizar las distribuciones de ingresos y riqueza. Para cualquier distribución, la curva de Lorenz L(F) se escribe en términos de PDF f o CDF F como

L()F)=∫ ∫ xmx()F)xf()x)dx∫ ∫ xmJUEGO JUEGO xf()x)dx=∫ ∫ 0Fx()F.)dF.∫ ∫ 01x()F.)dF.{displaystyle L(F)={frac {int ¿Por qué? ¿Por qué?

donde x(F) es la inversa de la CDF. Para la distribución de Pareto,

x()F)=xm()1− − F)1α α {displaystyle x(F)={frac {x_{mathrm}{(1-F)}{frac {1}{alpha }

y la curva de Lorenz se calcula para ser

L()F)=1− − ()1− − F)1− − 1α α ,{displaystyle L(F)=1-(1-F)^{1-{frac {1}{alpha }}}}}}

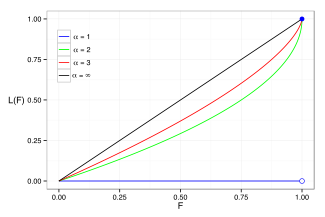
Para <math alttext="{displaystyle 00.α α ≤ ≤ 1{displaystyle 0 realizadasalpha leq 1}<img alt="{displaystyle 0 el denominador es infinito, rindiendo L=0. Ejemplos de la curva Lorenz para una serie de distribuciones de Pareto se muestran en el gráfico de la derecha.

Según Oxfam (2016), las 62 personas más ricas tienen tanta riqueza como la mitad más pobre de la población mundial. Podemos estimar el índice de Pareto que se aplicaría a esta situación. Letting ε equal 62/()7× × 109){displaystyle 62/(7times 10^{9}} tenemos:

L()1/2)=1− − L()1− − ε ε ){displaystyle L(1/2)=1-L(1-varepsilon)}

o

1− − ()1/2)1− − 1α α =ε ε 1− − 1α α {displaystyle 1-(1/2)^{1-{frac {1}{alpha }= 'varepsilon ^{1-{frac {1}{alpha }

La solución es que α equivale aproximadamente a 1,15, y aproximadamente el 9 % de la riqueza es propiedad de cada uno de los dos grupos. Pero en realidad, el 69% más pobre de la población adulta mundial posee solo alrededor del 3% de la riqueza.

El coeficiente Gini es una medida de la desviación de la curva Lorenz de la línea de distribución que es una línea que conecta [0, 0] y [1, 1], que se muestra en negro (αEn la parcela de Lorenz a la derecha. Específicamente, el coeficiente Gini es el doble del área entre la curva Lorenz y la línea de distribución. Luego se calcula el coeficiente Gini para la distribución de Pareto (para α α ≥ ≥ 1{displaystyle alpha geq 1}Para ser

G=1− − 2()∫ ∫ 01L()F)dF)=12α α − − 1{displaystyle G=1-2left(int _{0}^{1}L(F),dFright)={frac {1}{2alpha - Sí.

(ver Aaberge 2005).

Generación de variables aleatorias

Se pueden generar muestras aleatorias mediante el muestreo por transformada inversa. Dada una variable aleatoria U extraída de la distribución uniforme en el intervalo unitario (0, 1], la variable T dada por

T=xmU1/α α {displaystyle T={frac {x_{mathrm {m} } {U^{1/alpha }

es una distribución de Pareto. Si U se distribuye uniformemente en [0, 1), se puede intercambiar con (1 − U).