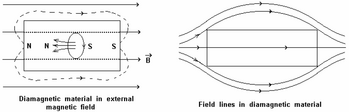
Diamagnetismo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

magnetismo ordinario, débil, repulsivo que todos los materiales poseen

El carbono pirolítico tiene una de las mayores constantes diamagnéticas de cualquier material de temperatura ambiente. Aquí una hoja de carbono pirolítica es levitada por su repulsión del fuerte campo magnético de imanes de neodimio.

Los materiales diamagnéticos son repelidos por un campo magnético; un campo magnético aplicado crea un campo magnético inducido en ellos en la dirección opuesta, provocando una fuerza repulsiva. Por el contrario, los materiales paramagnéticos y ferromagnéticos son atraídos por un campo magnético. El diamagnetismo es un efecto mecánico cuántico que ocurre en todos los materiales; cuando es la única contribución al magnetismo, el material se llama diamagnético. En sustancias paramagnéticas y ferromagnéticas, la débil fuerza diamagnética es superada por la fuerza de atracción de los dipolos magnéticos en el material. La permeabilidad magnética de los materiales diamagnéticos es menor que la permeabilidad del vacío, μ₀. En la mayoría de los materiales, el diamagnetismo es un efecto débil que solo puede ser detectado por instrumentos de laboratorio sensibles, pero un superconductor actúa como un fuerte diamagnet porque repele un campo magnético completamente desde su interior.

Interacción de material diamagnético en campo magnético.

El diamagnetismo se descubrió por primera vez cuando Anton Brugmans observó en 1778 que los campos magnéticos repelían el bismuto. En 1845, Michael Faraday demostró que era una propiedad de la materia y concluyó que todo material respondía (ya sea de forma diamagnética o paramagnética) a un campo magnético aplicado. Siguiendo una sugerencia de William Whewell, Faraday primero se refirió al fenómeno como diamagnético (el prefijo dia- significa a través o a través. i>), luego lo cambió a diamagnetismo.

En química se usa una regla general simple para determinar si una partícula (átomo, ion o molécula) es paramagnética o diamagnética: si todos los electrones en la partícula están emparejados, entonces la sustancia hecha de esta partícula es diamagnética; Si tiene electrones desapareados, entonces la sustancia es paramagnética.

Materiales

Materiales diamagnéticos notables
Material	χ_m [× 10^{; 5 -} (unidades de SI)]
Superconductor	−10⁵
carbono pirolítico	−40.9
Bismuth	−16.6
Neon	−6.74
Mercurio	−2.9
Plata	−2.6
Carbon (diamond)	−2.1
Lead	−1.8
Carbon (graphite)	−1.6
Copper	1.0−
Agua	−0,91

El diamagnetismo es una propiedad de todos los materiales y siempre contribuye débilmente a la respuesta del material a un campo magnético. Sin embargo, otras formas de magnetismo (como el ferromagnetismo o el paramagnetismo) son mucho más fuertes que, cuando hay múltiples formas diferentes de magnetismo en un material, la contribución diamagnética suele ser insignificante. Las sustancias en las que el comportamiento diamagnético es el efecto más fuerte se denominan materiales diamagnéticos o diamagnetos. Los materiales diamagnéticos son aquellos que algunas personas generalmente consideran no magnéticos e incluyen agua, madera, la mayoría de los compuestos orgánicos como el petróleo y algunos plásticos, y muchos metales, incluido el cobre, en particular los pesados con muchos electrones del núcleo, como el mercurio, el oro y el bismuto. Los valores de susceptibilidad magnética de varios fragmentos moleculares se denominan constantes de Pascal.

Los materiales diamagnéticos, como el agua o los materiales a base de agua, tienen una permeabilidad magnética relativa menor o igual a 1 y, por lo tanto, una susceptibilidad magnética menor o igual a 0, ya que la susceptibilidad se define como χ_v = μ_v − 1. Esto significa que los materiales diamagnéticos son repelidos por los campos magnéticos. Sin embargo, dado que el diamagnetismo es una propiedad tan débil, sus efectos no son observables en la vida cotidiana. Por ejemplo, la susceptibilidad magnética de los diamagnetos como el agua es χ_v = −9.05×10⁻⁶ . El material diamagnético más fuerte es el bismuto, χ_v = −1.66×10⁻⁴ , aunque el carbón pirolítico puede tener una susceptibilidad de χ_v = −4.00×10⁻⁴ en un plano. Sin embargo, estos valores son órdenes de magnitud más pequeños que el magnetismo exhibido por paramagnetos y ferromagnetos. Debido a que χ_v se deriva de la relación entre el campo magnético interno y el campo aplicado, es un valor adimensional.

En casos excepcionales, la contribución diamagnética puede ser más fuerte que la contribución paramagnética. Este es el caso del oro, que tiene una susceptibilidad magnética inferior a 0 (y, por lo tanto, es por definición un material diamagnético), pero cuando se mide cuidadosamente con dicroísmo circular magnético de rayos X, tiene una contribución paramagnética extremadamente débil que es superada por una más fuerte. contribución diamagnética.

Superconductores

Transition from ordinary conductivity (left) to superconductivity (right). En la transición, el superconductor expulsa el campo magnético y luego actúa como un diamagnet perfecto.

Los superconductores pueden considerarse diamagnetos perfectos (χ_v = −1), porque expulsan todos los campos magnéticos (excepto en una fina capa superficial) debido al efecto Meissner.

Demostraciones

Superficies de agua curvas

Si un imán potente (como un superimán) se cubre con una capa de agua (que es delgada en comparación con el diámetro del imán), el campo del imán repele significativamente el agua. Esto provoca un pequeño hoyuelo en la superficie del agua que puede verse por un reflejo en su superficie.

Levitación

Una rana viva levita dentro de un agujero vertical de 32 mm (1.26 pulgadas) de diámetro de un solenoide Bitter en un campo magnético de alrededor de 16 teslas en el Laboratorio de Magnetos de Campo Alto Nijmegen.

Los diamagnetos pueden levitar en equilibrio estable en un campo magnético, sin consumo de energía. El teorema de Earnshaw parece excluir la posibilidad de levitación magnética estática. Sin embargo, el teorema de Earnshaw se aplica solo a objetos con susceptibilidades positivas, como los ferromagnetos (que tienen un momento positivo permanente) y los paramagnetos (que inducen un momento positivo). Estos son atraídos por los máximos de campo, que no existen en el espacio libre. Los diamagnetos (que inducen un momento negativo) son atraídos por los mínimos de campo y puede haber un mínimo de campo en el espacio libre.

Un trozo delgado de grafito pirolítico, que es un material inusualmente fuertemente diamagnético, puede flotar de manera estable en un campo magnético, como el de los imanes permanentes de tierras raras. Esto se puede hacer con todos los componentes a temperatura ambiente, haciendo una demostración visualmente efectiva y relativamente conveniente del diamagnetismo.

La Universidad Radboud de Nijmegen, en los Países Bajos, ha llevado a cabo experimentos en los que se levitó con éxito agua y otras sustancias. Más espectacularmente, una rana viva (ver figura) fue levitada.

En septiembre de 2009, el Laboratorio de Propulsión a Chorro (JPL) de la NASA en Pasadena, California, anunció que había logrado levitar ratones utilizando un imán superconductor, un importante paso adelante ya que los ratones están biológicamente más cerca de los humanos que las ranas. JPL dijo que espera realizar experimentos sobre los efectos de la microgravedad en la masa ósea y muscular.

Experimentos recientes que estudian el crecimiento de cristales de proteína han llevado a una técnica que utiliza imanes potentes para permitir el crecimiento de formas que contrarrestan la gravedad de la Tierra.

Se puede construir un dispositivo casero simple para demostración con placas de bismuto y algunos imanes permanentes que hacen levitar un imán permanente.

Teoría

Los electrones de un material generalmente se asientan en orbitales, con una resistencia cero efectiva y actúan como bucles de corriente. Por lo tanto, podría imaginarse que los efectos del diamagnetismo en general serían comunes, ya que cualquier campo magnético aplicado generaría corrientes en estos bucles que se opondrían al cambio, de manera similar a los superconductores, que son esencialmente diamagnetos perfectos. Sin embargo, dado que los electrones se mantienen rígidamente en los orbitales por la carga de los protones y están aún más restringidos por el principio de exclusión de Pauli, muchos materiales presentan diamagnetismo, pero normalmente responden muy poco al campo aplicado.

El teorema de Bohr-Van Leeuwen demuestra que no puede haber diamagnetismo o paramagnetismo en un sistema puramente clásico. Sin embargo, la teoría clásica de Langevin para el diamagnetismo da la misma predicción que la teoría cuántica. La teoría clásica se da a continuación.

Diamagnetismo de Langevin

La teoría del diamagnetismo de Paul Langevin (1905) se aplica a materiales que contienen átomos con capas cerradas (ver dieléctricos). Un campo con intensidad $B$ , aplicado a un electrón con carga $e$ y masa $m$ , da lugar a la precesión de Larmor con frecuencia $ω = eB / 2 m$ . El número de revoluciones por unidad de tiempo es $ω / 2 π$ , por lo que la corriente para un átomo con $Z$ electrones es (en unidades SI)

I = -frac{Ze^2B}{4 pi m}.

El momento magnético de un bucle corriente es igual a los tiempos actuales de la zona del bucle. Supongamos que el campo está alineado con el $z$ Axis. El área de bucle promedio se puede administrar como $scriptstyle pileftlanglerho^2rightrangle$ , donde $scriptstyle leftlanglerho^2rightrangle$ es la distancia media cuadrada de los electrones perpendiculares al $z$ Axis. Por lo tanto, el momento magnético

mu = -frac{Ze^2B}{4 m}langlerho^2rangle.

Si la distribución del cargo es es esféricamente simétrica, podemos suponer que la distribución $x,y,z$ las coordenadas son independientes y se distribuyen de forma idéntica. Entonces... $scriptstyle leftlangle x^2 rightrangle ;=; leftlangle y^2 rightrangle ;=; leftlangle z^2 rightrangle ;=; frac{1}{3}leftlangle r^2 rightrangle$ , donde $scriptstyle leftlangle r^2 rightrangle$ es la distancia media cuadrada de los electrones del núcleo. Por lo tanto, $scriptstyle leftlangle rho^2 rightrangle ;=; leftlangle x^2rightrangle ;+; leftlangle y^2 rightrangle ;=; frac{2}{3}leftlangle r^2 rightrangle$ . Si $n$ es el número de átomos por volumen de unidad, la susceptibilidad diamagnética del volumen en unidades SI es

{displaystyle chi ={frac {mu _{0}nmu }{B}}=-{frac {mu _{0}e^{2}Zn}{6m}}langle r^{2}rangle.}

En los átomos, la susceptibilidad de Langevin es del mismo orden de magnitud que la susceptibilidad paramagnética de Van Vleck.

En metales

La teoría de Langevin no es la imagen completa de los metales porque también hay electrones no localizados. La teoría que describe el diamagnetismo en un gas de electrones libres se llama diamagnetismo de Landau, en honor a Lev Landau, y en su lugar considera el débil campo que se contrarresta que se forma cuando los electrones' las trayectorias son curvas debido a la fuerza de Lorentz. Sin embargo, el diamagnetismo de Landau debe contrastarse con el paramagnetismo de Pauli, un efecto asociado con la polarización de electrones deslocalizados. giros. Para el caso a granel de un sistema 3D y campos magnéticos bajos, la susceptibilidad diamagnética (volumen) se puede calcular utilizando la cuantización de Landau, que en unidades SI es

{displaystyle chi =-mu _{0}{frac {e^{2}}{12pi ^{2}mhbar }}{sqrt {2mE_{rm {F}}}},}

Donde ${displaystyle E_{rm {F}}}$ es la energía de Fermi. Esto equivale a ${displaystyle -mu _{0}mu _{rm {B}}^{2}g(E_{rm {F}})/3}$ , exactamente ${textstyle -1/3}$ Pauli paramagnetic susceptibilidad, donde ${displaystyle mu _{rm {B}}=ehbar /2m}$ es el imán Bohr $g(E)$ es la densidad de estados (número de estados por energía por volumen). Esta fórmula tiene en cuenta la degeneración de giro de los portadores (spin 1⁄2 electrones).

En los semiconductores dopados, la relación entre las susceptibilidades de Landau y Pauli puede cambiar debido a que la masa efectiva de los portadores de carga difiere de la masa del electrón en el vacío, lo que aumenta la contribución diamagnética. La fórmula presentada aquí solo se aplica a granel; en sistemas confinados como puntos cuánticos, la descripción se altera debido al confinamiento cuántico. Además, para campos magnéticos fuertes, la susceptibilidad de los electrones deslocalizados oscila en función de la intensidad del campo, un fenómeno conocido como efecto De Haas-Van Alphen, también descrito teóricamente por primera vez por Landau.

Contenido relacionado

Más resultados...