Diagrama de Venn

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Ejemplo del diagrama de Venn — Ejemplo de diagrama de Venn

Un diagrama de Venn es un estilo de diagrama ampliamente utilizado que muestra la relación lógica entre conjuntos, popularizado por John Venn en la década de 1880. Los diagramas se utilizan para enseñar teoría elemental de conjuntos y para ilustrar relaciones de conjuntos simples en probabilidad, lógica, estadística, lingüística e informática. Un diagrama de Venn usa curvas cerradas simples dibujadas en un plano para representar conjuntos. Muy a menudo, estas curvas son círculos o elipses.

Antes de Venn se habían propuesto ideas similares. Christian Weise en 1712 (Nucleus Logicoe Wiesianoe) y Leonhard Euler (Cartas a una princesa alemana) en 1768, por ejemplo, propusieron ideas similares. La idea fue popularizada por Venn en Lógica simbólica, Capítulo V "Representación esquemática", 1881.

Detalles

Un diagrama de Venn también puede llamarse diagrama de conjuntos o diagrama lógico. Es un diagrama que muestra todas las relaciones lógicas posibles entre una colección finita de conjuntos diferentes. Estos diagramas representan elementos como puntos en el plano y conjuntos como regiones dentro de curvas cerradas. Un diagrama de Venn consta de múltiples curvas cerradas superpuestas, generalmente círculos, cada uno de los cuales representa un conjunto. Los puntos dentro de una curva etiquetada S representan elementos del conjunto S, mientras que los puntos fuera del límite representan elementos que no están en el conjunto S. Esto se presta a visualizaciones intuitivas; por ejemplo, el conjunto de todos los elementos que son miembros de ambos conjuntos S y T, denotado S ∩ T y leído "la intersección de S y T ", se representa visualmente por el área de superposición de las regiones S y T.

En los diagramas de Venn, las curvas se superponen de todas las formas posibles, mostrando todas las relaciones posibles entre los conjuntos. Por lo tanto, son un caso especial de los diagramas de Euler, que no necesariamente muestran todas las relaciones. Los diagramas de Venn fueron concebidos alrededor de 1880 por John Venn. Se utilizan para enseñar teoría elemental de conjuntos, así como para ilustrar relaciones de conjuntos simples en probabilidad, lógica, estadística, lingüística e informática.

Un diagrama de Venn en el que el área de cada forma es proporcional al número de elementos que contiene se denomina diagrama de Venn proporcional al área (o escalado).

Diagrama de Venn para representar las diferencias entre los alfabetos latino, cirílico y griego

Ejemplo

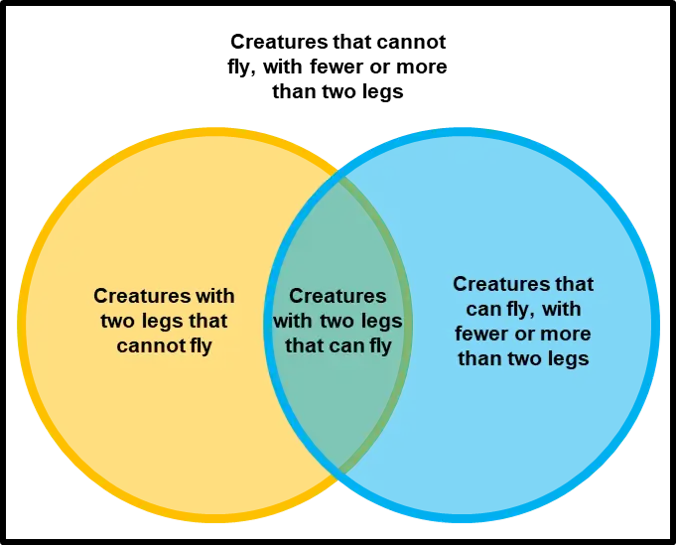
Este ejemplo involucra dos conjuntos, A y B, representados aquí como círculos de colores. El círculo naranja, conjunto A, representa todos los tipos de criaturas vivientes que tienen dos patas. El círculo azul, conjunto B, representa a los seres vivos que pueden volar. Cada tipo de criatura por separado se puede imaginar como un punto en algún lugar del diagrama. Los seres vivos que pueden volar y tienen dos patas, por ejemplo, los loros, se encuentran en ambos conjuntos, por lo que corresponden a puntos en la región donde se superponen los círculos azul y naranja. Esta región superpuesta solo contendría aquellos elementos (en este ejemplo, criaturas) que son miembros tanto del conjunto A (criaturas de dos patas) como del conjunto B (criaturas voladoras).

Los humanos y los pingüinos son bípedos, y también lo están en el círculo naranja, pero como no pueden volar, aparecen en la parte izquierda del círculo naranja, donde no se superpone con el círculo azul. Los mosquitos pueden volar, pero tienen seis patas, no dos, por lo que el punto para los mosquitos está en la parte del círculo azul que no se superpone con el naranja. Las criaturas que no tienen dos patas y no pueden volar (por ejemplo, las ballenas y las arañas) estarían todas representadas por puntos fuera de ambos círculos.

La región combinada de los conjuntos A y B se llama la unión de A y B, denotada por A ∪ B. La unión en este caso contiene todos los seres vivos que tienen dos patas o pueden volar (o ambos).

La región incluida tanto en A como en B, donde los dos conjuntos se superponen, se denomina intersección de A y B, denotada por A ∩ B. En este ejemplo, la intersección de los dos conjuntos no está vacía, porque hay puntos que representan criaturas que están en los círculos naranja y azul.

Historia

Los diagramas de Venn fueron introducidos en 1880 por John Venn en un artículo titulado "Sobre la representación esquemática y mecánica de proposiciones y razonamientos" en Philosophical Magazine and Journal of Science, sobre las diferentes formas de representar proposiciones mediante diagramas. El uso de este tipo de diagramas en la lógica formal, según Frank Ruskey y Mark Weston, "no es una historia fácil de rastrear, pero es cierto que los diagramas que se asocian popularmente con Venn, de hecho, se originaron mucho antes. están correctamente asociados con Venn, sin embargo, porque examinó y formalizó exhaustivamente su uso, y fue el primero en generalizarlos".

El propio Venn no usó el término "diagrama de Venn" y se refirió a su invento como "Círculos de Euler". Por ejemplo, en la oración inicial de su artículo de 1880, Venn escribe: "Los esquemas de representación diagramática se han introducido tan familiarmente en los tratados lógicos durante el último siglo, que muchos lectores, incluso aquellos que no han hecho ningún estudio profesional de la lógica, pueden se supone que debe estar familiarizado con la naturaleza general y el objeto de tales dispositivos. De estos esquemas, uno solo, a saber, el comúnmente llamado 'círculos eulerianos', ha encontrado alguna aceptación general..." Lewis Carroll (Charles L. Dodgson) incluye "Método de diagramas de Venn", así como "Método de diagramas de Euler" en un "Apéndice, dirigido a los maestros"(4ª edición publicada en 1896). El término "diagrama de Venn" fue utilizado más tarde por Clarence Irving Lewis en 1918, en su libro A Survey of Symbolic Logic.

Los diagramas de Venn son muy similares a los diagramas de Euler, que fueron inventados por Leonhard Euler en el siglo XVIII. Margaret Baron ha señalado que Leibniz (1646-1716) produjo diagramas similares antes que Euler en el siglo XVII, pero gran parte de ellos no se publicaron. También observa diagramas tipo Euler incluso anteriores de Ramon Llull en el siglo XIII.

En el siglo XX, los diagramas de Venn se desarrollaron aún más. David Wilson Henderson demostró, en 1963, que la existencia de un diagrama de n -Venn con simetría rotacional de n-veces implicaba que n era un número primo. También demostró que tales diagramas de Venn simétricos existen cuando n es cinco o siete. En 2002, Peter Hamburger encontró diagramas de Venn simétricos para n = 11 y en 2003, Griggs, Killian y Savage demostraron que existen diagramas de Venn simétricos para todos los demás números primos. Estos resultados combinados muestran que existen diagramas de Venn rotacionalmente simétricos, si y solo si n es un número primo.

Los diagramas de Venn y los diagramas de Euler se incorporaron como parte de la enseñanza de la teoría de conjuntos, como parte del nuevo movimiento matemático en la década de 1960. Desde entonces, también se han adoptado en el currículo de otros campos como la lectura.

Visión de conjunto

Intersección de dos conjuntos $~Acap B$
unión de dos conjuntos $~Ataza B$
Diferencia simétrica de dos conjuntos ${ estilo de visualización A ~ triángulo ~ B}$
Complemento relativo de A (izquierda) en B (derecha) $A^{c}cap B~=~Bsetminus A$
Complemento absoluto de A en U $A^{c}~=~Usetminus A$

Un diagrama de Venn se construye con una colección de curvas cerradas simples dibujadas en un plano. Según Lewis, el "principio de estos diagramas es que las clases [o conjuntos ] se representen por regiones en tal relación entre sí que todas las posibles relaciones lógicas de estas clases puedan indicarse en el mismo diagrama. Es decir, el diagrama inicialmente deja espacio para cualquier relación posible de las clases, y la relación real o dada puede especificarse indicando que alguna región en particular es nula o no es nula".

Los diagramas de Venn normalmente comprenden círculos superpuestos. El interior del círculo representa simbólicamente los elementos del conjunto, mientras que el exterior representa elementos que no son miembros del conjunto. Por ejemplo, en un diagrama de Venn de dos conjuntos, un círculo puede representar el grupo de todos los objetos de madera, mientras que el otro círculo puede representar el conjunto de todas las mesas. La región superpuesta, o intersección, representaría entonces el conjunto de todas las mesas de madera. Se pueden emplear formas distintas de los círculos, como se muestra a continuación, en los diagramas de conjuntos superiores del propio Venn. Los diagramas de Venn generalmente no contienen información sobre los tamaños relativos o absolutos (cardinalidad) de los conjuntos. Es decir, son diagramas esquemáticos generalmente no dibujados a escala.

Los diagramas de Venn son similares a los diagramas de Euler. Sin embargo, un diagrama de Venn para n conjuntos de componentes debe contener las 2 zonas hipotéticamente posibles, que corresponden a alguna combinación de inclusión o exclusión en cada uno de los conjuntos de componentes. Los diagramas de Euler contienen solo las zonas realmente posibles en un contexto dado. En los diagramas de Venn, una zona sombreada puede representar una zona vacía, mientras que en un diagrama de Euler, la zona correspondiente falta en el diagrama. Por ejemplo, si un conjunto representa productos lácteos y otro quesos, el diagrama de Venn contiene una zona para quesos que no son productos lácteos. Suponiendo que en el contexto quesosignifica algún tipo de producto lácteo, el diagrama de Euler tiene la zona del queso completamente contenida dentro de la zona del producto lácteo; no hay zona para el (inexistente) queso no lácteo. Esto significa que a medida que aumenta el número de contornos, los diagramas de Euler suelen ser menos complejos visualmente que el diagrama de Venn equivalente, especialmente si el número de intersecciones no vacías es pequeño.

La diferencia entre los diagramas de Euler y Venn se puede ver en el siguiente ejemplo. Tome los tres conjuntos:

$A={1,,2,,5}$
$B={1,,6}$
$C={4,,7}$

Los diagramas de Euler y Venn de esos conjuntos son:

diagrama de Euler

Extensiones a un mayor número de conjuntos

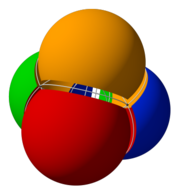
Los diagramas de Venn normalmente representan dos o tres conjuntos, pero hay formas que permiten números más altos. A continuación, cuatro esferas que se cruzan forman el diagrama de Venn de mayor orden que tiene la simetría de un símplex y puede representarse visualmente. Las 16 intersecciones corresponden a los vértices de un tesseract (o las celdas de un 16 celdas, respectivamente).

Para un mayor número de conjuntos, es inevitable cierta pérdida de simetría en los diagramas. Venn estaba ansioso por encontrar "figuras simétricas... elegantes en sí mismas" que representaran un mayor número de conjuntos, e ideó un elegante diagrama de cuatro conjuntos usando elipses (ver más abajo). También dio una construcción para diagramas de Venn para cualquier número de conjuntos, donde cada curva sucesiva que delimita un conjunto se intercala con curvas anteriores, comenzando con el diagrama de tres círculos.

Construcción de Venn para cuatro juegos.
Construcción de Venn para cinco juegos.
Construcción de Venn para seis juegos.
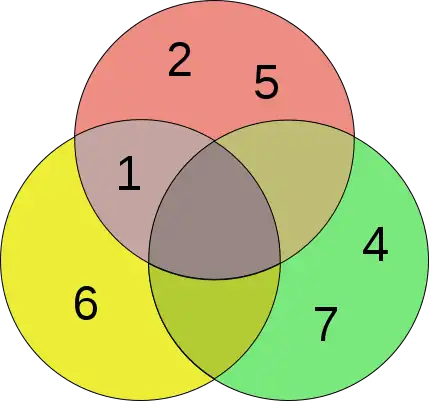
Diagrama de cuatro conjuntos de Venn usando elipses
No ejemplo: este diagrama de Euler no es un diagrama de Venn para cuatro conjuntos, ya que solo tiene 13 regiones (excluyendo el exterior); no hay región donde solo se encuentren los círculos amarillo y azul, o solo el rojo y el verde.
Diagrama de Venn de cinco conjuntos que utiliza elipses congruentes en una disposición simétrica de rotación quíntuple ideada por Branko Grünbaum. Las etiquetas se han simplificado para una mayor legibilidad; por ejemplo, A denota A ∩ B ∩ C ∩ D ∩ E, mientras que BCE denota A ∩ B ∩ C ∩ D ∩ E.
Diagrama de Venn de seis conjuntos hecho solo de triángulos (versión interactiva)

Diagramas de Edwards-Venn

tres conjuntos
cuatro conjuntos
cinco juegos
Seis conjuntos

Anthony William Fairbank Edwards construyó una serie de diagramas de Venn para un mayor número de conjuntos segmentando la superficie de una esfera, que se conoció como diagramas de Edwards-Venn. Por ejemplo, tres conjuntos se pueden representar fácilmente tomando tres hemisferios de la esfera en ángulo recto (x = 0, y = 0 y z = 0). Se puede agregar un cuarto conjunto a la representación, tomando una curva similar a la costura de una pelota de tenis, que se enrolla hacia arriba y hacia abajo alrededor del ecuador, y así sucesivamente. Los conjuntos resultantes se pueden volver a proyectar en un plano para obtener diagramas de rueda dentada con un número creciente de dientes, como se muestra aquí. Estos diagramas se idearon mientras se diseñaba una vidriera en memoria de Venn.

Otros diagramas

Los diagramas de Edwards-Venn son topológicamente equivalentes a los diagramas ideados por Branko Grünbaum, que se basaban en la intersección de polígonos con un número creciente de lados. También son representaciones bidimensionales de hipercubos.

Henry John Stephen Smith ideó diagramas de n conjuntos similares usando curvas sinusoidales con la serie de ecuaciones ${displaystyle y_{i}={frac {sin left(2^{i}xright)}{2^{i}}}{text{ donde }}0leq ileq n- 2{text{ y }}ien mathbb {N}.}$

Charles Lutwidge Dodgson (también conocido como Lewis Carroll) ideó un diagrama de cinco conjuntos conocido como el cuadrado de Carroll. Joaquín y Boyles, por otro lado, propusieron reglas complementarias para el diagrama de Venn estándar, con el fin de dar cuenta de ciertos casos problemáticos. Por ejemplo, con respecto a la cuestión de representar enunciados singulares, sugieren considerar el círculo del diagrama de Venn como una representación de un conjunto de cosas y utilizar la lógica de primer orden y la teoría de conjuntos para tratar los enunciados categóricos como enunciados sobre conjuntos. Además, proponen tratar las declaraciones singulares como declaraciones sobre la pertenencia a un conjunto. Entonces, por ejemplo, para representar la afirmación "a es F" en este diagrama de Venn modificado, se puede colocar una letra pequeña "a" dentro del círculo que representa el conjunto F.

Conceptos relacionados

Los diagramas de Venn corresponden a tablas de verdad para las proposiciones $x en A$ , $xen B$ , etc., en el sentido de que cada región del diagrama de Venn corresponde a una fila de la tabla de verdad. Este tipo también se conoce como diagrama de Johnston. Otra forma de representar conjuntos es con los diagramas R de John F. Randolph.

Contenido relacionado

Más resultados...