Diagrama de Pourbaix

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Parcela de fases termodinámicamente estables de un sistema electroquímico acuoso

En electroquímica, y más generalmente en química de soluciones, un diagrama de Pourbaix, también conocido como diagrama de potencial/pH, E_{Hdiagrama de pH} o un diagrama de pE/pH es un gráfico de posibles fases termodinámicamente estables (es decir,, en equilibrio químico) de un sistema electroquímico acuoso. . Los límites (50 %/50 %) entre las especies químicas predominantes (iones acuosos en solución o fases sólidas) están representados por líneas. Como tal, un diagrama de Pourbaix se puede leer de manera muy similar a un diagrama de fase estándar con un conjunto diferente de ejes. De manera similar a los diagramas de fases, no tienen en cuenta la velocidad de reacción ni los efectos cinéticos. Además del potencial y el pH, las concentraciones de equilibrio también dependen, por ejemplo, de la temperatura, la presión y la concentración. Los diagramas de Pourbaix se dan comúnmente a temperatura ambiente, presión atmosférica y concentraciones molares de 10⁻⁶ y al cambiar cualquiera de estos parámetros se obtendrá un diagrama diferente.

Los diagramas llevan el nombre de Marcel Pourbaix (1904–1998), el químico belga nacido en Rusia que los inventó.

Denominación

Los diagramas de Pourbaix también se conocen como diagramas E_H-pH debido al etiquetado de los dos ejes.

Diagrama

El eje vertical está etiquetado como E_H para el potencial de voltaje con respecto al electrodo de hidrógeno estándar (SHE) calculado mediante la ecuación de Nernst. La "H" significa hidrógeno, aunque se pueden usar otros estándares, y son solo para temperatura ambiente.

Para una reacción redox reversible descrita por el siguiente equilibrio químico:

a A + b B ⇌ c C + d D

Con la constante de equilibrio correspondiente $K$ :

{displaystyle K={frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}

La ecuación de Nernst es:

{displaystyle E_{text{H}}=E^{0}-{frac {RT}{zF}}ln {K},}

{displaystyle E_{text{H}}=E^{0}-{frac {RT}{zF}}ln {frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}

a veces formulado como:

{displaystyle E_{text{H}}=E^{0}-{frac {V_{T}lambda }{z}}log {frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}

o, más simplemente, expresado directamente numéricamente como:

{displaystyle E_{text{H}}=E^{0}-{frac {0.05916}{z}}log {frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}

donde:

${displaystyle V_{T}=RT/Fapprox 0.02569}$ volt es el voltaje térmico o la " pendiente norte" a temperatura estándar

λ = ln(10) ${displaystyle V_{T}lambda approx 0.05916}$ Volt.

El eje horizontal está etiquetado como pH para la función −log de la actividad del ion H⁺.

{displaystyle {text{pH}}=-log _{10}(a_{{ce {H+}}})=log _{10}left({frac {1}{a_{{ce {H+}}}}}right).}

Las líneas en el diagrama de Pourbaix muestran las condiciones de equilibrio, es decir, donde las actividades son iguales, para las especies a cada lado de esa línea. A ambos lados de la línea, se dirá que una forma de la especie es predominante.

Para poder dibujar la posición de las líneas con la ecuación de Nernst, se debe definir la actividad de las especies químicas en equilibrio. Por lo general, la actividad de una especie se aproxima a la concentración (para especies solubles) o a la presión parcial (para gases). Se deben utilizar los mismos valores para todas las especies presentes en el sistema.

Para especies solubles, las líneas a menudo se dibujan para concentraciones de 1 M o 10⁻⁶ M. A veces se dibujan líneas adicionales para otras concentraciones.

Si el diagrama involucra el equilibrio entre una especie disuelta y un gas, la presión generalmente se establece en P⁰ = 1 atm = 101325 Pa, la presión mínima requerida para el gas Evolución a partir de una solución acuosa en condiciones estándar.

Además, los cambios de temperatura y concentración de iones solvatados en solución desplazarán las líneas de equilibrio de acuerdo con la ecuación de Nernst.

Los diagramas tampoco tienen en cuenta los efectos cinéticos, lo que significa que las especies que se muestran como inestables podrían no reaccionar en ningún grado significativo en la práctica.

Un diagrama simplificado de Pourbaix indica regiones de "inmunidad", "corrosión" y "pasividad", en lugar de la especie estable. Por tanto, dan una guía sobre la estabilidad de un metal particular en un entorno específico. La inmunidad significa que el metal no es atacado, mientras que la corrosión muestra que se producirá un ataque general. La pasivación ocurre cuando el metal forma una capa estable de un óxido u otra sal en su superficie, siendo el mejor ejemplo la relativa estabilidad del aluminio debido a la capa de alúmina que se forma en su superficie cuando se expone al aire.

Sistemas químicos aplicables

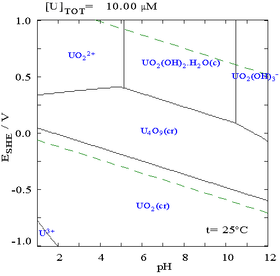
Si bien estos diagramas se pueden dibujar para cualquier sistema químico, es importante tener en cuenta que la adición de un agente aglutinante de metales (ligando) a menudo modificará el diagrama. Por ejemplo, carbonato (CO2−3) tiene un gran efecto sobre el diagrama del uranio. (Ver diagramas a la derecha). La presencia de trazas de ciertas especies, como los iones cloruro, también puede afectar en gran medida la estabilidad de ciertas especies al destruir las capas pasivantes.

Limitaciones

Aunque los diagramas de Pourbaix son útiles para estimar el potencial de corrosión de metales, tienen, sin embargo, algunas limitaciones importantes:

El equilibrio siempre se asume, aunque en la práctica puede diferir.
El diagrama no proporciona información sobre las tasas de corrosión reales.
No se aplica a las aleaciones.
No indica si la pasivación (en forma de óxidos o hidroxidos) es protectora o no. Difusión de iones de oxígeno a través de capas de óxido fino son posibles.
Excluye la corrosión por iones de cloruro (Cl⁻, Cl³⁺ etc.).
Normalmente sólo se aplica a la temperatura de 25 °C (77 °F), que se asume por defecto. Los diagramas Pourbaix para temperaturas superiores existen.

Expresión de la ecuación de Nernst en función del pH

El ${displaystyle E_{h}}$ y pH de una solución están relacionados por la ecuación Nernst como comúnmente representado por un diagrama Pourbaix () ${displaystyle E_{h}}$ – pH plot). ${displaystyle E_{h}}$ denota explícitamente ${displaystyle E_{text{red}}}$ expresado contra el electrodo de hidrógeno estándar (SHE). Para una ecuación de media célula, convencionalmente escrita como una reacción de reducción (i.e., electrones aceptados por un oxidante en el lado izquierdo):

<math alttext="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" xmlns="http://www.w3.org/1998/Math/MathML">aA+bB+hH++ze− − ↽ ↽ − − − − ⇀ ⇀ cC+dD{displaystyle a,A+b,B+h,{ce {H+}+z,e^{-}quad {ce {}quad c,C+d,D}<img alt="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/21d6729acf60e5eaffa170e8d2ef03fc0e334405" style="vertical-align: -0.505ex; width:41.61ex; height:2.843ex;"/>

La constante de equilibrio $K$ de esta reacción de reducción es:

{displaystyle K={frac {{C}^{c}{D}^{d}}{{A}^{a}{B}^{b}{{ce {H+}}}^{h}}}={frac {(gamma _{c})^{c}left[Cright]^{c} (gamma _{d})^{d}left[Dright]^{d}}{(gamma _{a})^{a}left[Aright]^{a} (gamma _{b})^{b}left[Bright]^{b} (gamma _{h+})^{h}left[{ce {H+}}right]^{h}}}={frac {(gamma _{c})^{c}(gamma _{d})^{d}}{(gamma _{a})^{a}(gamma _{b})^{b}(gamma _{h})^{h}}}{text{×}}{frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}left[{ce {H+}}right]^{h}}}}

donde los frenos rizados { } indican actividades ( $a$ ), frenos rectángulos [ ] denote molar o concentraciones de molal ( $C$ ), ${displaystyle gamma }$ representan los coeficientes de actividad, y los coeficientes estoichiométricos se muestran como exponentes.

Las actividades corresponden a concentraciones termodinámicas y tienen en cuenta las interacciones electrostáticas entre iones presentes en la solución. Cuando las concentraciones no son demasiado altas, la actividad ( ${displaystyle a_{i}}$ ) puede estar relacionado con la concentración mensurable ( ${displaystyle C_{i}}$ ) por una relación lineal con el coeficiente de actividad ( ${displaystyle gamma _{i}}$ ):

{displaystyle a_{i}=gamma _{i},C_{i}}

El potencial de reducción estándar de media célula ${displaystyle E_{text{red}}^{ominus }}$ es dado por

{displaystyle E_{text{red}}^{ominus }({text{volt}})=-{frac {Delta G^{ominus }}{zF}}}

Donde ${displaystyle Delta G^{ominus }}$ es el cambio de energía libre estándar Gibbs, $z$ es el número de electrones involucrados, y $F$ es la constante del Faraday. La ecuación Nernst relaciona pH y ${displaystyle E_{h}}$ como sigue:

{displaystyle E_{h}=E_{text{red}}=E_{text{red}}^{ominus }-{frac {RT}{zF}}log left({frac {{C}^{c}{D}^{d}}{{A}^{a}{B}^{b}}}right)-{frac {RT,h}{zF}}{text{pH}}}

En la siguiente, la pendiente Nernst (o tensión térmica) ${displaystyle V_{T}=RT/F}$ se utiliza, que tiene un valor de 0.02569... V en STP. Cuando se utilizan logaritmos base-10, V_T λ = 0,05916... V en STP donde λ = ln[10] = 2.3026.

{displaystyle E_{h}=E_{text{red}}=E_{text{red}}^{ominus }-{frac {0.05916}{z}}log left({frac {{C}^{c}{D}^{d}}{{A}^{a}{B}^{b}}}right)-{frac {0.05916,h}{z}}{text{pH}}}

Esta ecuación es la ecuación de una línea recta para ${displaystyle E_{text{red}}}$ como una función de pH con una pendiente de ${displaystyle -0.05916,left({frac {h}{z}}right)}$ volt (pH no tiene unidades).

Esta ecuación predice menor ${displaystyle E_{text{red}}}$ a valores de pH más altos. Esto se observa para la reducción de O₂ en H₂O, o OH⁻, y para la reducción de H⁺ en H₂. ${displaystyle E_{text{red}}}$ es entonces a menudo notado como ${displaystyle E_{h}}$ para indicar que se refiere al electrodo de hidrógeno estándar (SHE) cuyo ${displaystyle E_{text{red}}}$ = 0 por convención bajo condiciones estándar (T = 298.15 K = 25 °C = 77 F, P_gas = 1 atm (1.013 bar), concentraciones = 1 M y por lo tanto pH = 0).

Cálculo de un diagrama de Pourbaix

Cuando las actividades ( ${displaystyle a_{i}}$ ) se puede considerar igual al molar, o el molal, concentraciones ( ${displaystyle C_{i}}$ ) en concentraciones suficientemente diluidas cuando los coeficientes de actividad ( ${displaystyle gamma _{i}}$ ) tienden a uno, el término reagrupar todos los coeficientes de actividad es igual a uno, y la ecuación Nernst se puede escribir simplemente con las concentraciones ( ${displaystyle C_{i}}$ ) denotado aquí con frenos cuadrados [ ]:

{displaystyle E_{h}=E_{text{red}}=E_{text{red}}^{ominus }-{frac {0.05916}{z}}log left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)-{frac {0.05916,h}{z}}{text{pH}}}

Hay tres tipos de límites de línea en un diagrama de Pourbaix: vertical, horizontal e inclinado.

Línea límite vertical

Cuando no se intercambian electrones (z = 0), el equilibrio entre $A$ , B, $C$ y $D$ solo depende de $[H +]$ y no se ve afectado por el potencial del electrodo. En este caso, la reacción es una reacción ácido-base clásica que implica únicamente la protonación/desprotonación de especies disueltas. La línea límite será una línea vertical en un valor particular de pH. La ecuación de reacción se puede escribir:

<math alttext="{displaystyle a,A+b,B+h,{ce {H+}}quad {ce {}}quad c,C+d,D}" xmlns="http://www.w3.org/1998/Math/MathML">aA+bB+hH+↽ ↽ − − − − ⇀ ⇀ cC+dD{displaystyle a,A+b,B+h,{ce {H+}quad {ce {}quad c,C+d,D}<img alt="{displaystyle a,A+b,B+h,{ce {H+}}quad {ce {}}quad c,C+d,D}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/54bc2cf4202e219571a44fcfd4d773d360907670" style="vertical-align: -0.505ex; width:34.7ex; height:2.843ex;"/>

y el balance energético está escrito como ${displaystyle Delta G^{circ }=-RTln K}$ , donde $K$ es la constante del equilibrio:

{displaystyle K={frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}left[{ce {H+}}right]^{h}}}}

Así:

{displaystyle Delta G^{circ }=-RTln left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}left[{ce {H+}}right]^{h}}}right)}

o, en logaritmos de base 10,

{displaystyle Delta G^{circ }=-RTlambda ,left(log left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)+h,{ce {pH}}right)}

que puede resolverse para el valor particular del pH.

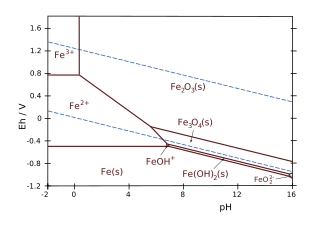
Por ejemplo, considere el sistema de hierro y agua, y la línea de equilibrio entre el ion férrico Fe³⁺ y la hematita Fe₂O₃. La ecuación de reacción es:

<math alttext="{displaystyle {ce {2 Fe^{3+}(aq) + 3 H_2 O (l) Fe_2 O_3 (s) + 6 H^+ (aq)}}}" xmlns="http://www.w3.org/1998/Math/MathML">2Fe3+()aq)+3H2O()l)↽ ↽ − − − − ⇀ ⇀ Fe2O3()s)+6H+()aq){displaystyle {ce {2 Fe^{3+}(aq) + 3 H_2 O (l) <= Confío Fe_2 O_3 (s) + 6 H^+ (aq)}}}<img alt="{displaystyle {ce {2 Fe^{3+}(aq) + 3 H_2 O (l) Fe_2 O_3 (s) + 6 H^+ (aq)}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/69c0b7c3ed5d4385990b71f71773b497f9cb149d" style="vertical-align: -1.005ex; width:48.154ex; height:3.343ex;"/>

que tiene ${displaystyle Delta G^{circ }=-8242.5,mathrm {J/mol} }$ . El pH de la línea vertical en el diagrama Pourbaix se puede calcular:

{displaystyle {ce {pH}}=-{frac {1}{6}}left({frac {Delta G^{circ }}{RTlambda }}+log left({frac {{ce {[Fe2O3]}}}{{ce {[Fe^{3+}]^2[H2O]^3}}}}right)right)}

Porque las actividades (o las concentraciones) de las fases sólidas y del agua son iguales a la unidad:
[Fe₂O₃] = [H₂O] = 1, el pH solo depende de la concentración en Fe³⁺
>:

{displaystyle {ce {pH}}=-{frac {1}{6}}left({frac {Delta G^{circ }}{RTlambda }}+log left({frac {1}{[{ce {Fe^{3+}}}]^{2}}}right)right)}

En STP, para [Fe³⁺] = 10⁻⁶, esto produce un pH = 1,76.

Límite límite horizontal

Cuando los iones H⁺ y OH⁻ no participan en la reacción, la línea límite es horizontal e independiente del pH.
La ecuación de reacción queda así escrita:

<math alttext="{displaystyle a,A+b,B+z,e^{-}quad {ce {}}quad c,C+d,Dqquad (z>0{text{, but without}} {ce {H+}})}" xmlns="http://www.w3.org/1998/Math/MathML">aA+bB+ze− − ↽ ↽ − − − − ⇀ ⇀ cC+dD()z■0, pero sin H+){fnMicrosoft Sans Serif}quad c,C+d,Dqquad (z {fnMicrosoft Sans, pero sin}fnMicrosoft, {ce {fn}}}<img alt="{displaystyle a,A+b,B+z,e^{-}quad {ce {}}quad c,C+d,Dqquad (z>0{text{, but without}} {ce {H+}})}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f5244b19ba1acf678e9fd433c99dcc4d75d8219f" style="vertical-align: -0.838ex; width:62.607ex; height:3.176ex;"/>

Como, la energía libre estándar Gibbs ${displaystyle Delta G^{circ }=-RTln K}$ :

{displaystyle Delta G^{circ }=-RTln left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)}

Usando la definición del potencial del electrodo ∆G = -zFE, donde F es la constante de Faraday, esto se puede reescribir como Ecuación de Nernst:

{displaystyle E_{h}={E^{circ }}-{frac {V_{T}}{z}}ln left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)}

o, usando logaritmos de base 10:

{displaystyle E_{h}={E^{circ }}-{frac {V_{T}lambda }{z}}log left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)}

Para el equilibrio Fe²⁺
>/Fe, tomado como ejemplo aquí, considerando la línea límite entre Fe²⁺ y Fe³⁺, la ecuación de semirreacción es:

<math alttext="{displaystyle {ce {Fe^3+ (aq) + e^- Fe^2+ (aq)}}}" xmlns="http://www.w3.org/1998/Math/MathML">Fe3+()aq)+e− − ↽ ↽ − − − − ⇀ ⇀ Fe2+()aq){fnMicrosoft Sans Serif}}<img alt="{displaystyle {ce {Fe^3+ (aq) + e^- Fe^2+ (aq)}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d9276aa6cc66a221c43d030f650520accd8ab67c" style="vertical-align: -0.838ex; width:28.196ex; height:3.176ex;"/>

Desde H⁺ Los iones no están involucrados en esta reacción redox, es independiente de pH. E^o = 0,7171 V con solo un electrón involucrado en la reacción de redox. El potencial E_h es una función de temperatura a través del voltaje térmico ${displaystyle V_{T}}$ y depende directamente de la relación de las concentraciones de Fe²⁺
y Fe³⁺
iones:

{displaystyle E_{h}={E^{circ }}-V_{T}lambda log left({frac {{ce {[Fe^{2+}]}}}{{ce {[Fe^{3+}]}}}}right)}

Para ambas especies iónicas a la misma concentración (por ejemplo, ${displaystyle 10^{-6}mathrm {M} }$ ) en STP, log 1 = 0, así que, ${displaystyle E_{h}=E^{circ }=0.771,mathrm {V} }$ , y el límite será una línea horizontal en E_h = 0,71 voltios. El potencial variará con temperatura.

Línea límite inclinada

En este caso, están involucrados tanto electrones como iones H⁺ y el potencial del electrodo es función del pH. La ecuación de reacción se puede escribir:

<math alttext="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" xmlns="http://www.w3.org/1998/Math/MathML">aA+bB+hH++ze− − ↽ ↽ − − − − ⇀ ⇀ cC+dD{displaystyle a,A+b,B+h,{ce {H+}+z,e^{-}quad {ce {}quad c,C+d,D}<img alt="{displaystyle a,A+b,B+h,{ce {H+}}+z,e^{-}quad {ce {}}quad c,C+d,D}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/21d6729acf60e5eaffa170e8d2ef03fc0e334405" style="vertical-align: -0.505ex; width:41.61ex; height:2.843ex;"/>

Utilizando las expresiones para la energía libre en términos de potenciales, el balance energético viene dado por una ecuación de Nernst:

{displaystyle E_{h}={E^{circ }}-{frac {V_{T}lambda }{z}}left(log left({frac {left[Cright]^{c}left[Dright]^{d}}{left[Aright]^{a}left[Bright]^{b}}}right)+h,{ce {pH}}right)}

Para el ejemplo del hierro y el agua, considerando la línea límite entre el ion ferroso Fe²⁺ y la hematita Fe₂O₃, la la ecuación de reacción es:

<math alttext="{displaystyle {ce {Fe2O3(s) + 6 H+(aq) + 2 e^- 2 Fe^{2+}(aq) + 3 H2O(l)}}}" xmlns="http://www.w3.org/1998/Math/MathML">Fe2O3()s)+6H+()aq)+2e− − ↽ ↽ − − − − ⇀ ⇀ 2Fe2+()aq)+3H2O()l){displaystyle {ce {Fe2O3(s) + 6 H+(aq) + 2 e^- <= fieltro 2 Fe^{2+}(aq) + 3 H2O(l)}}}<img alt="{displaystyle {ce {Fe2O3(s) + 6 H+(aq) + 2 e^- 2 Fe^{2+}(aq) + 3 H2O(l)}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9a15338c4713e886a4fc15a2635cb7d7d85a834c" style="vertical-align: -1.005ex; width:55.087ex; height:3.343ex;"/>

con

{displaystyle E^{circ }=0.728mathrm {V} }

La ecuación de la línea límite, expresada en logaritmos de base 10 es:

{displaystyle E_{h}={E^{circ }}-{frac {V_{T}lambda }{2}}left(log left({frac {{ce {[Fe^{2+}]^2[H2O]^3}}}{{ce {[Fe2O3]}}}}right)+6 {ce {pH}}right)}

Así, las actividades o concentraciones de las fases sólidas y del agua siempre se consideran iguales a la unidad por convención en la definición de la constante de equilibrio $K$ : [Fe₂O₃] = [H₂O] = 1.

La ecuación de Nernst se limita así a las especies disueltas Fe²⁺
y H+ se escribe como:

{displaystyle E_{h}={E^{circ }}-{frac {V_{T}lambda }{2}}left(log {ce {[Fe^{2+}]^2}}+6 {ce {pH}}right)}

Para, [Fe²⁺] = 10⁻⁶ M, esto produce:

{displaystyle E_{h}={1.0826}-{0.1775} {pH}quad ({text{in volts}})}

Observe la pendiente negativa (-0,1775) de esta línea en un diagrama E_h–pH.

La región de estabilidad del agua

Diagrama de Pourbaix para agua, incluyendo regiones de estabilidad para agua, oxígeno e hidrógeno a temperatura y presión estándar (STP). La escala vertical (ordinada) es el potencial de electrodo (de un electrodo de hidrógeno o no interaccionante) en relación con un electrodo SHE, la escala horizontal (abscissa) es el pH del electrolito (otros no interactuación). Suponiendo que no haya sobrepotencia, por encima de la línea superior la condición de equilibrio implica la producción de gas de oxígeno, y el oxígeno se deshará del electrodo hasta alcanzar el equilibrio, o el agua totalmente consumida. Del mismo modo, debajo de la línea inferior, la condición de equilibrio implica la producción de gas de hidrógeno, y el hidrógeno se deshará del electrodo hasta alcanzar el equilibrio, o el agua totalmente consumida.

En muchos casos, las posibles condiciones en un sistema están limitadas por la región de estabilidad del agua. En el diagrama de Pourbaix para el uranio presentado aquí arriba, los límites de estabilidad del agua están marcados por dos líneas verdes discontinuas, y la región de estabilidad del agua se encuentra entre estas dos líneas. También se representa aquí junto a las dos líneas rojas discontinuas en el diagrama simplificado de Pourbaix restringido únicamente a la región de estabilidad del agua.

En condiciones altamente reductoras (baja E_H), el agua se reduce a hidrógeno de acuerdo con:

H2(g)}}}" xmlns="http://www.w3.org/1998/Math/MathML">2H++2e− − restablecimiento restablecimiento H2()g){displaystyle {ce {2 H+ + 2e^-] H2(g)}}} H2(g)}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/57af1ff32799d409d73a922c9b4aa4da2442ad07" style="vertical-align: -1.005ex; width:22.602ex; height:3.176ex;"/>

(a bajo pH)

H2(g) + 2 OH^-}}}" xmlns="http://www.w3.org/1998/Math/MathML">2H2O+2e− − restablecimiento restablecimiento H2()g)+2Oh.− − {displaystyle {ce {2 H2O + 2e^-] H2(g) + 2 OH^-}} H2(g) + 2 OH^-}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/960d43cbb1c84a1b68642db803ad9acfab554f42" style="vertical-align: -1.005ex; width:33.405ex; height:3.176ex;"/>

(en alta pH)

Usando la ecuación de Nernst, estableciendo E⁰ = 0 V como se define por convención para el electrodo de hidrógeno estándar (SHE, que sirve como referencia en la serie de potenciales de reducción) y la fugacidad del gas hidrógeno (correspondiente a la actividad química de un gas) en 1, la ecuación para la línea de estabilidad inferior del agua en el diagrama de Pourbaix a temperatura y presión estándar es:

{displaystyle E_{{ce {H}}}=-V_{T}lambda ,{ce {pH}}}

{displaystyle E_{{ce {H}}}=-0.05916,{ce {pH}}}

Por debajo de esta línea, el agua se reduce a hidrógeno y, por lo general, no será posible pasar más allá de esta línea mientras todavía haya agua presente en el sistema a reducir.

En consecuencia, en condiciones altamente oxidantes (alta E_H), el agua se oxida en oxígeno gaseoso de acuerdo con:

4 H+ + O2(g) + 4e^-}}}" xmlns="http://www.w3.org/1998/Math/MathML">2H2Orestablecimiento restablecimiento 4H++O2()g)+4e− − {displaystyle {ce {2 H2O] 4 H+ + O2(g) + 4e^-}} 4 H+ + O2(g) + 4e^-}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/51223222f22a13ec80dee30a0b734a47eb5b2521" style="vertical-align: -1.005ex; width:31.662ex; height:3.176ex;"/>

(a bajo pH)

O2(g) + 2 H_2O + 4e^-}}}" xmlns="http://www.w3.org/1998/Math/MathML">4Oh.− − restablecimiento restablecimiento O2()g)+2H2O+4e− − {fnMicrosoft Sans Serif} O2(g) + 2 H_2O + 4e^-}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9d2985242f3f34152ec958a96f13e2882eb51118" style="vertical-align: -1.005ex; width:33.47ex; height:3.176ex;"/>

(en alta pH)

Usando la ecuación de Nernst como arriba, pero con E⁰ = −ΔG⁰_H₂O/ 2F = 1,229 V para la oxidación del agua, da un límite superior de estabilidad del agua en función del valor del pH:

{displaystyle E_{{ce {H}}}=E^{0}-V_{T}lambda ,{ce {pH}}}

{displaystyle E_{{ce {H}}}=1.229V-0.05916,{ce {pH}}}

a temperatura y presión estándar. Por encima de esta línea, el agua se oxida para formar oxígeno gaseoso y, por lo general, no será posible pasar más allá de esta línea mientras todavía haya agua presente en el sistema para oxidarse.

Las dos líneas de estabilidad superior e inferior tienen la misma pendiente negativa (−59 mV/unidad de pH), son paralelas en un diagrama de Pourbaix y el potencial de reducción disminuye con el pH.

Aplicaciones

Los diagramas de Pourbaix tienen muchas aplicaciones en diferentes campos relacionados con por ejemplo, problemas de corrosión, geoquímica y ciencias ambientales. El uso correcto del diagrama de Pourbaix ayudará a arrojar luz no sólo sobre la naturaleza de las especies presentes en la solución acuosa o en las fases sólidas, sino que también puede ayudar a comprender el mecanismo de reacción.

Concepto de pe en química ambiental

Los diagramas de Pourbaix se utilizan ampliamente para describir el comportamiento de especies químicas en la hidrosfera. En este contexto, el potencial de reducción $pe$ se utiliza a menudo en lugar de $E H$ . La principal ventaja es trabajar directamente con una escala logarítmica. $pe$ es un número adimensional y puede relacionarse fácilmente con $E H$ por la ecuación:

{displaystyle pe={frac {E_{H}}{V_{T}lambda }}={frac {E_{H}}{0.05916}}=16.903,{text{×}},E_{H}}

¿Dónde? ${displaystyle V_{T}={frac {RT}{F}}}$ es el voltaje térmico, con $R$ , la constante de gas (8.314 J⋅K⁻¹⋅mol⁻¹), $T$ , la temperatura absoluta en Kelvin (298.15 K = 25 °C = 77 °F), y $F$ , la constante Faraday (96 485 coulomb/mol de e⁻). Lambda, λ = ln(10) ♥ 2.3026.

Además,

{displaystyle pe=-log[e^{-}]}

, una expresión con una forma similar a la de pH.

Los valores

$pe$ en química ambiental oscilan entre −12 y +25, ya que a potenciales bajos o altos el agua se reducirá respectivamente. u oxidado. En aplicaciones ambientales, la concentración de especies disueltas generalmente se establece en un valor entre 10⁻² M y 10⁻⁵ M para la determinación de las líneas de equilibrio.

Galería

Fe-H₂O
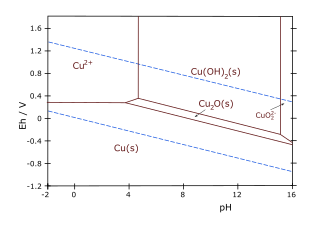
Cu-H₂O
Au-H₂O
Al-H₂O
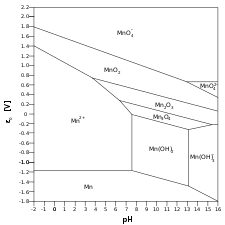
Mn-H₂O
Zn-H₂O-CO₃^2-
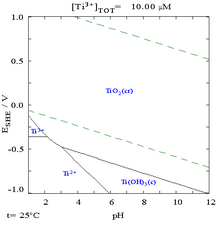
Ti-H₂O

Contenido relacionado

Más resultados...