Diagrama de araña

En matemáticas, un diagrama de araña unitario añade puntos existenciales a un diagrama de Euler o de Venn. Los puntos indican la existencia de un atributo descrito por la intersección de contornos en el diagrama de Euler. Estos puntos pueden unirse formando una forma de araña. Los puntos unidos representan una unión "o" condición, también conocida como disyunción lógica.

A diagrama de araña es una expresión booleana que implica diagramas de araña unitaria y los símbolos lógicos ∧ ∧ ,Alternativa Alternativa ,¬ ¬ {displaystyle landlorlnot }. Por ejemplo, puede consistir en la conjunción de dos diagramas de araña, la disyunción de dos diagramas de araña, o la negación de un diagrama de araña.

Ejemplo

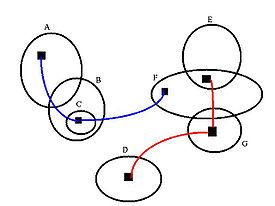
En la imagen mostrada, las siguientes conjunciones son evidentes en el diagrama de Euler.

A∧ ∧ B{displaystyle Aland B}

B∧ ∧ C{displaystyle Bland C}

F∧ ∧ E{displaystyle Fland E}

G∧ ∧ F{displaystyle Gland F}

En el universo del discurso definido por este diagrama de Euler, además de las conjunciones especificadas anteriormente, todos los conjuntos desde A hasta G, excepto C, están disponibles por separado. El conjunto C solo está disponible como un subconjunto de B. A menudo, en diagramas complicados, los conjuntos únicos y/o las conjunciones pueden quedar oscurecidos por otras combinaciones de conjuntos.

Las dos arañas del ejemplo corresponden a las siguientes expresiones lógicas:

• Araña roja: ()F∧ ∧ E)Alternativa Alternativa ()G)Alternativa Alternativa ()D){displaystyle (Fland E)lor (G)lor (D)}
• Araña azul: ()A)Alternativa Alternativa ()C∧ ∧ B)Alternativa Alternativa ()F){displaystyle (A)lor (Cland B)lor (F)}