Desviación estándar

Compartir Imprimir Citar

Cuartiles de desviación típica — Cuartiles de desviación

La desviación estándar o desviación típica es un índice numérico de la dispersión de un conjunto de datos (o población). Mientras mayor es la desviación estándar, mayor es la dispersión de la población. La desviación estándar es un promedio de las desviaciones individuales de cada observación con respecto a la media de una distribución. Así, la desviación estándar mide el grado de dispersión o variabilidad. En primer lugar, midiendo la diferencia entre cada valor del conjunto de datos y la media del conjunto de datos. Luego, sumando todas estas diferencias individuales para dar el total de todas las diferencias. Por último, dividiendo el resultado por el número total de observaciones (normalmente representado por la letra “n”) para llegar a un promedio de las distancias entre cada observación individual y la media. Este promedio de las distancias es la desviación estándar y de esta manera representa dispersión.

La desviación estándar puede abreviarse SD y se representa más comúnmente en los textos matemáticos y las ecuaciones con la letra griega minúscula sigma σ, para la desviación estándar de la población, o la letra latina s, para la desviación estándar de la muestra.

La desviación estándar de una variable aleatoria, muestra, población estadística, conjunto de datos o distribución de probabilidad es la raíz cuadrada de su varianza. Es algebraicamente más simple, aunque en la práctica menos robusto, que la desviación absoluta promedio. Una propiedad útil de la desviación estándar es que, a diferencia de la varianza, se expresa en la misma unidad que los datos.

La desviación estándar de una población o muestra y el error estándar de una estadística (por ejemplo, de la media muestral) son bastante diferentes, pero están relacionados. El error estándar de la media muestral es la desviación estándar del conjunto de medias que se encontraría extrayendo un número infinito de muestras repetidas de la población y calculando una media para cada muestra. El error estándar de la media resulta ser igual a la desviación estándar de la población dividida por la raíz cuadrada del tamaño de la muestra, y se estima usando la desviación estándar de la muestra dividida por la raíz cuadrada del tamaño de la muestra. Por ejemplo, el error estándar de una encuesta (lo que se informa como el margen de error de la encuesta) es la desviación estándar esperada de la media estimada si la misma encuesta se realizara varias veces. Por lo tanto,

En ciencias, es común informar tanto la desviación estándar de los datos (como una estadística de resumen) como el error estándar de la estimación (como una medida del error potencial en los hallazgos). Por convención, solo los efectos a más de dos errores estándar de una expectativa nula se consideran "estadísticamente significativos", una salvaguardia contra conclusiones espurias que en realidad se deben a un error de muestreo aleatorio.

Cuando solo se dispone de una muestra de datos de una población, el término desviación estándar de la muestra o desviación estándar de la muestra puede referirse a la cantidad antes mencionada aplicada a esos datos, o a una cantidad modificada que es una estimación no sesgada de la desviación estándar de la población (la desviación estándar de toda la población).

Importancia

Matemáticamente, la desviación estándar podría, a primera vista, parecer algo complicada. Sin embargo, es en realidad un concepto extremadamente simple. En realidad no importa si usted no sabe calcular con exactitud la desviación estándar, siempre y cuando usted comprenda claramente el concepto.

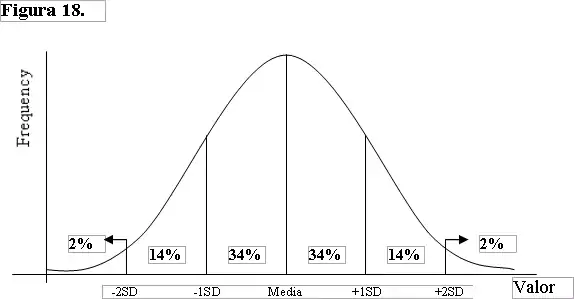
La desviación estándar es un indicador en extremo valioso con muchas aplicaciones. Por ejemplo, los estadísticos saben que cuando un conjunto de datos se distribuye de manera “normal”, el 68% de las observaciones de la distribución tiene un valor que se encuentra a menos de una desviación estándar de la media. También saben que el 96% de todas las observaciones tiene un valor no es mayor a la media más o menos dos desviaciones estándar (la Figura 18 grafica esta información).

Ejemplos básicos

Desviación estándar de la población de las calificaciones de ocho estudiantes

Suponga que la población total de interés son ocho estudiantes en una clase en particular. Para un conjunto finito de números, la desviación estándar de la población se calcula sacando la raíz cuadrada del promedio de las desviaciones al cuadrado de los valores restados de su valor promedio. Las notas de una clase de ocho estudiantes (es decir, una población estadística) son los siguientes ocho valores:

$2, 4, 4, 4, 5, 5, 7, 9.$

Estos ocho puntos de datos tienen la media (promedio) de 5:

${displaystyle mu ={frac {2+4+4+4+5+5+7+9}{8}}={frac {40}{8}}=5.}$

Primero, calcule las desviaciones de cada punto de datos de la media y eleve al cuadrado el resultado de cada uno:

${displaystyle {begin{matriz}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0 (4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\(4-5)^{2}= (-1)^{2}=1&&(7-5)^{2}=2^{2}=4\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16.\end{matriz}}}$

La varianza es la media de estos valores:

${displaystyle sigma ^{2}={frac {9+1+1+1+0+0+4+16}{8}}={frac {32}{8}}=4.}$

y la desviación estándar de la población es igual a la raíz cuadrada de la varianza:

${ estilo de visualización sigma = { sqrt {4}} = 2.}$

Esta fórmula es válida solo si los ocho valores con los que comenzamos forman la población completa. Si, en cambio, los valores fueran una muestra aleatoria extraída de una gran población de padres (por ejemplo, eran 8 estudiantes elegidos al azar e independientemente de una clase de 2 millones), entonces se divide por 7 (que es n − 1) en lugar de 8 (que es n) en el denominador de la última fórmula, y el resultado es ${textstyle s={sqrt {32/7}}aprox. 2,1.}$ En ese caso, el resultado de la fórmula original se llamaría desviación estándar de la muestra y se denotaría por s en lugar de $sigma.$ Dividir por n − 1 en lugar de por nda una estimación no sesgada de la varianza de la población de padres más grande. Esto se conoce como corrección de Bessel. Aproximadamente, la razón de esto es que la fórmula para la varianza de la muestra se basa en calcular las diferencias de las observaciones de la media de la muestra, y la media de la muestra en sí misma se construyó para estar lo más cerca posible de las observaciones, por lo que simplemente dividir por n subestimaría el variabilidad.

Desviación estándar de la estatura promedio para hombres adultos

Si la población de interés tiene una distribución aproximadamente normal, la desviación estándar proporciona información sobre la proporción de observaciones por encima o por debajo de ciertos valores. Por ejemplo, la estatura promedio de los hombres adultos en los Estados Unidos es de unas 70 pulgadas (177,8 cm), con una desviación estándar de unas 3 pulgadas (7,62 cm). Esto significa que la mayoría de los hombres (alrededor del 68 %, suponiendo una distribución normal) tienen una altura dentro de las 3 pulgadas (7,62 cm) de la media (67 a 73 pulgadas (170,18 a 185,42 cm)), una desviación estándar, y casi todos los hombres (aproximadamente el 95 %) tiene una altura dentro de las 6 pulgadas (15,24 cm) de la media (64 a 76 pulgadas (162,56 a 193,04 cm)), dos desviaciones estándar. Si la desviación estándar fuera cero, todos los hombres medirían exactamente 70 pulgadas (177,8 cm) de altura. Si la desviación estándar fuera de 50,8 cm (20 pulgadas), los hombres tendrían alturas mucho más variables, con un rango típico de alrededor de 50 a 90 pulgadas (127 a 228,6 cm). Tres desviaciones estándar representan el 99,7 % de la muestra de población que se está estudiando, suponiendo que la distribución es normal o en forma de campana (consulte la regla 68–95–99,7, o laregla empírica, para más información).

Definición de valores de población

Sea μ el valor esperado (el promedio) de la variable aleatoria X con densidad f (x):

{displaystyle mu equiv operatorname {E} [X]=int _{-infty}^{+infty}xf(x),dx}

La desviación estándar σ de X se define como

{displaystyle sigma equiv {sqrt {operatorname {E} left[(X-mu)^{2}right]}}={sqrt {int_{-infty}^{+ infty}(x-mu)^{2}f(x),dx}},}

que se puede demostrar que es igual

${textstyle {sqrt {operatorname {E} left[X^{2}right]-(operatorname {E} [X])^{2}}}.}$

Usando palabras, la desviación estándar es la raíz cuadrada de la varianza de X.

La desviación estándar de una distribución de probabilidad es la misma que la de una variable aleatoria que tenga esa distribución.

No todas las variables aleatorias tienen una desviación estándar. Si la distribución tiene colas anchas que se extienden hasta el infinito, es posible que la desviación estándar no exista, porque la integral podría no converger. La distribución normal tiene colas que van hasta el infinito, pero su media y desviación estándar existen, porque las colas disminuyen lo suficientemente rápido. La distribución de Pareto con parámetro ${ estilo de visualización alfa en (1,2]}$ tiene una media, pero no una desviación estándar (en términos generales, la desviación estándar es infinita). La distribución de Cauchy no tiene media ni desviación estándar.

Variable aleatoria discreta

En el caso de que X tome valores aleatorios de un conjunto finito de datos x ₁, x ₂, …, x _N, con cada valor teniendo la misma probabilidad, la desviación estándar es

{displaystyle sigma ={sqrt {{frac {1}{N}}left[(x_{1}-mu)^{2}+(x_{2}-mu)^{2} +cdots +(x_{N}-mu)^{2}right]}},{text{ donde }}mu ={frac {1}{N}}(x_{1}+ cpuntos +x_{N}),}

o, usando la notación de suma,

{displaystyle sigma ={sqrt {{frac {1}{N}}sum _{i=1}^{N}(x_{i}-mu)^{2}}},{ texto{ donde }}mu ={frac {1}{N}}sum _{i=1}^{N}x_{i}.}

Si, en lugar de tener probabilidades iguales, los valores tienen probabilidades diferentes, sea x ₁ una probabilidad p ₁, x ₂ una probabilidad p ₂, …, x _N una probabilidad p _N. En este caso, la desviación estándar será

{displaystyle sigma ={sqrt {sum _{i=1}^{N}p_{i}(x_{i}-mu)^{2}}},{text{ donde }} mu =suma _{i=1}^{N}p_{i}x_{i}.}

Variable aleatoria continua

La desviación estándar de una variable aleatoria X continua de valor real con función de densidad de probabilidad p (x) es

{displaystyle sigma ={sqrt {int _{mathbf {X} }(x-mu)^{2},p(x),dx}},{text{ donde }} mu =int _{mathbf {X} }x,p(x),dx,}

y donde las integrales son integrales definidas tomadas para x que se extienden sobre el conjunto de valores posibles de la variable aleatoria X.

En el caso de una familia paramétrica de distribuciones, la desviación estándar se puede expresar en términos de los parámetros. Por ejemplo, en el caso de la distribución log-normal con parámetros μ y σ, la desviación estándar es

{displaystyle {sqrt {left(e^{sigma ^{2}}-1right)e^{2mu +sigma ^{2}}}}.}

Estimación

Uno puede encontrar la desviación estándar de una población completa en casos (como pruebas estandarizadas) donde se muestrea a cada miembro de una población. En los casos en que eso no se puede hacer, la desviación estándar σ se estima examinando una muestra aleatoria tomada de la población y calculando una estadística de la muestra, que se usa como una estimación de la desviación estándar de la población. Tal estadística se denomina estimador, y el estimador (o el valor del estimador, es decir, la estimación) se denomina desviación estándar de la muestra y se denota por s (posiblemente con modificadores).

A diferencia del caso de estimar la media poblacional, para el cual la media muestral es un estimador simple con muchas propiedades deseables (imparcial, eficiente, máxima verosimilitud), no existe un único estimador para la desviación estándar con todas estas propiedades, y la estimación imparcial de la desviación estándar es un problema muy complicado desde el punto de vista técnico. La mayoría de las veces, la desviación estándar se estima usando la desviación estándar de la muestra corregida (usando N − 1), definida a continuación, y esto a menudo se denomina "desviación estándar de la muestra", sin calificadores. Sin embargo, otros estimadores son mejores en otros aspectos: el estimador no corregido (usando N) produce un error cuadrático medio más bajo, mientras que usando N − 1,5 (para la distribución normal) elimina casi por completo el sesgo.

Desviación estándar de la muestra no corregida

La fórmula para la desviación estándar de la población (de una población finita) se puede aplicar a la muestra, utilizando el tamaño de la muestra como el tamaño de la población (aunque el tamaño real de la población de la que se extrae la muestra puede ser mucho mayor). Este estimador, denotado por s _N, se conoce como la desviación estándar de la muestra no corregida o, a veces, la desviación estándar de la muestra (considerada como la población total), y se define de la siguiente manera:

{displaystyle s_{N}={sqrt {{frac {1}{N}}sum _{i=1}^{N}left(x_{i}-{bar {x}} derecha)^{2}}},}

donde ${displaystyle {x_{1},,x_{2},,ldots,,x_{N}}}$ son los valores observados de los elementos de la muestra, y ${ barra {x}}$ es el valor medio de estas observaciones, mientras que el denominador N representa el tamaño de la muestra: esta es la raíz cuadrada de la varianza de la muestra, que es el promedio de las desviaciones al cuadrado sobre la media muestral.

Este es un estimador consistente (converge en probabilidad al valor de la población a medida que el número de muestras llega al infinito), y es la estimación de máxima verosimilitud cuando la población tiene una distribución normal. Sin embargo, este es un estimador sesgado, ya que las estimaciones son generalmente demasiado bajas. El sesgo disminuye a medida que crece el tamaño de la muestra, cayendo como 1/ N y, por lo tanto, es más significativo para tamaños de muestra pequeños o moderados; porque 75}">el sesgo es inferior al 1%. Por lo tanto, para tamaños de muestra muy grandes, la desviación estándar de la muestra no corregida es generalmente aceptable. Este estimador también tiene un error cuadrático medio uniformemente más pequeño que la desviación estándar de la muestra corregida.

Desviación estándar de la muestra corregida

Si la varianza muestral sesgada (el segundo momento central de la muestra, que es una estimación sesgada hacia abajo de la varianza poblacional) se usa para calcular una estimación de la desviación estándar de la población, el resultado es

${displaystyle s_{N}={sqrt {{frac {1}{N}}sum _{i=1}^{N}left(x_{i}-{bar {x}} derecha)^{2}}}.}$

Aquí, tomar la raíz cuadrada introduce un mayor sesgo hacia abajo, por la desigualdad de Jensen, debido a que la raíz cuadrada es una función cóncava. El sesgo en la varianza se corrige fácilmente, pero el sesgo de la raíz cuadrada es más difícil de corregir y depende de la distribución en cuestión.

Se obtiene un estimador insesgado de la varianza aplicando la corrección de Bessel, usando N − 1 en lugar de N para obtener la varianza muestral insesgada, denotada como s:

${displaystyle s^{2}={frac {1}{N-1}}sum _{i=1}^{N}left(x_{i}-{bar {x}}right)^{2}.}$

Este estimador es imparcial si existe la varianza y los valores de la muestra se extraen de forma independiente con reemplazo. N − 1 corresponde al número de grados de libertad en el vector de desviaciones de la media,

${displaystyle textstyle (x_{1}-{bar {x}},;dots,;x_{n}-{bar {x}}).}$

Tomar raíces cuadradas reintroduce el sesgo (porque la raíz cuadrada es una función no lineal, que no conmuta con la expectativa), lo que produce la desviación estándar de la muestra corregida, denotada por s:

${displaystyle s={sqrt {{frac {1}{N-1}}sum _{i=1}^{N}left(x_{i}-{bar {x}}right)^{2}}}.}$

Como se explicó anteriormente, mientras que s es un estimador no sesgado de la varianza de la población, s sigue siendo un estimador sesgado de la desviación estándar de la población, aunque notablemente menos sesgado que la desviación estándar de la muestra no corregida. Este estimador se usa comúnmente y generalmente se conoce simplemente como la "desviación estándar de la muestra". El sesgo aún puede ser grande para muestras pequeñas (N menos de 10). A medida que aumenta el tamaño de la muestra, la cantidad de sesgo disminuye. Obtenemos más información y la diferencia entre ${ fracción {1}{N}}$ y ${displaystyle {frac{1}{N-1}}}$ se hace más pequeña.

Desviación estándar de muestra imparcial

Para la estimación imparcial de la desviación estándar, no existe una fórmula que funcione en todas las distribuciones, a diferencia de la media y la varianza. En cambio, s se utiliza como base y se escala mediante un factor de corrección para producir una estimación imparcial. Para la distribución normal, un estimador insesgado viene dado por s / c ₄, donde el factor de corrección (que depende de N) viene dado en términos de la función Gamma, y es igual a:

$c_{4}(N),=,{sqrt {frac {2}{N-1}}},,,{frac {Gamma left({frac {N}{ 2}}right)}{Gamma left({frac {N-1}{2}}right)}}.$

Esto surge porque la distribución muestral de la desviación estándar muestral sigue una distribución chi (escala) y el factor de corrección es la media de la distribución chi.

Se puede dar una aproximación reemplazando N − 1 con N − 1.5, lo que da: ${displaystyle {hat {sigma }}={sqrt {{frac {1}{N-1.5}}sum _{i=1}^{N}left(x_{i}-{ barra {x}}derecha)^{2}}},}$

El error en esta aproximación decae cuadráticamente (como 1/ N), y es adecuado para todas las muestras excepto para las más pequeñas o con la mayor precisión: para N = 3, el sesgo es igual al 1,3 %, y para N = 9, el sesgo ya es menor del 0,1%.

Una aproximación más precisa es reemplazar ${ estilo de visualización N-1.5}$ arriba con ${ estilo de visualización N-1.5+1/(8(N-1))}$ .

Para otras distribuciones, la fórmula correcta depende de la distribución, pero una regla general es utilizar el mayor refinamiento de la aproximación: ${displaystyle {hat {sigma }}={sqrt {{frac {1}{N-1.5-{frac {1}{4}}gamma_{2}}}sum_{i =1}^{N}izquierda(x_{i}-{bar {x}}derecha)^{2}}},}$

donde γ ₂ denota el exceso de curtosis de la población. El exceso de curtosis puede conocerse de antemano para ciertas distribuciones o estimarse a partir de los datos.

Intervalo de confianza de una desviación estándar muestreada

La desviación estándar que obtenemos al muestrear una distribución no es en sí misma absolutamente precisa, tanto por razones matemáticas (explicadas aquí por el intervalo de confianza) como por razones prácticas de medición (error de medición). El efecto matemático se puede describir mediante el intervalo de confianza o IC.

Con k = 1, ${ estilo de visualización q_ {0,025} = 0,000982}$ y ${ estilo de visualización q_ {0,975} = 5,024}$ . Los recíprocos de las raíces cuadradas de estos dos números nos dan los factores 0.45 y 31.9 dados arriba.

Una población más grande de N = 10 tiene 9 grados de libertad para estimar la desviación estándar. Los mismos cálculos anteriores nos dan en este caso un IC del 95 % que va desde 0,69 × SD hasta 1,83 × SD. Entonces, incluso con una población de muestra de 10, la SD real aún puede ser casi un factor 2 más alta que la SD muestreada. Para una población de muestra N = 100, esto se reduce a 0,88 × SD a 1,16 × SD. Para estar más seguros de que la SD muestreada está cerca de la SD real, necesitamos muestrear una gran cantidad de puntos.

Estas mismas fórmulas se pueden usar para obtener intervalos de confianza sobre la varianza de los residuos de un ajuste de mínimos cuadrados bajo la teoría normal estándar, donde k es ahora el número de grados de libertad para el error.

Límites en la desviación estándar

Para un conjunto de N > 4 datos que abarcan un rango de valores R, el límite superior de la desviación estándar s viene dado por s = 0,6R. Una estimación de la desviación estándar para N > 100 datos considerados aproximadamente normales se deriva de la heurística de que el 95 % del área bajo la curva normal se encuentra aproximadamente a dos desviaciones estándar a cada lado de la media, de modo que, con una probabilidad del 95 %, el rango total de valores R representa cuatro desviaciones estándar de modo que s ≈ R/4. Esta llamada regla del rango es útil en la estimación del tamaño de la muestra, ya que el rango de valores posibles es más fácil de estimar que la desviación estándar. Otros divisores K(N)del rango tales que s ≈ R/K(N) están disponibles para otros valores de N y para distribuciones no normales.

Identidades y propiedades matemáticas

La desviación estándar es invariable ante cambios de ubicación y se escala directamente con la escala de la variable aleatoria. Así, para una constante c y variables aleatorias X e Y: ${displaystyle {begin{alineado}sigma (c)&=0\sigma (X+c)&=sigma (X),\sigma (cX)&=|c|sigma (X).end{alineado}}}$

La desviación estándar de la suma de dos variables aleatorias se puede relacionar con sus desviaciones estándar individuales y la covarianza entre ellas: $sigma (X+Y)={sqrt {operatorname {var} (X)+operatorname {var} (Y)+2,operatorname {cov} (X,Y)}}.,$

donde ${ estilo de visualización estilo de texto nombre del operador {var} , = , sigma ^ {2}}$ y ${ estilo de visualización estilo de texto nombre del operador {cov}}$ representan la varianza y la covarianza, respectivamente.

El cálculo de la suma de las desviaciones al cuadrado se puede relacionar con momentos calculados directamente a partir de los datos. En la siguiente fórmula, la letra E se interpreta como el valor esperado medio, es decir, la media. ${displaystyle sigma (X)={sqrt {operatorname {E} left[(X-operatorname {E} [X])^{2}right]}}={sqrt {operatorname { E} left[X^{2}right]-(operatorname {E} [X])^{2}}}.}$

La desviación estándar de la muestra se puede calcular como: ${displaystyle s(X)={sqrt {frac {N}{N-1}}}{sqrt {operatorname {E} left[(X-operatorname {E} [X])^{ 2}derecho]}}.}$

Para una población finita con probabilidades iguales en todos los puntos, tenemos ${displaystyle {sqrt {{frac {1}{N}}sum _{i=1}^{N}left(x_{i}-{bar {x}}right)^{2 }}}={sqrt {{frac {1}{N}}left(sum _{i=1}^{N}x_{i}^{2}right)-{bar {x }}^{2}}}={sqrt {left({frac {1}{N}}sum _{i=1}^{N}x_{i}^{2}right)- left({frac {1}{N}}sum _{i=1}^{N}x_{i}right)^{2}}},}$

lo que significa que la desviación estándar es igual a la raíz cuadrada de la diferencia entre el promedio de los cuadrados de los valores y el cuadrado del valor promedio.

Consulte la fórmula computacional para la varianza como prueba y un resultado análogo para la desviación estándar de la muestra.

Interpretación y aplicación

Una desviación estándar grande indica que los puntos de datos pueden alejarse de la media y una desviación estándar pequeña indica que están agrupados muy cerca de la media.

Por ejemplo, cada una de las tres poblaciones {0, 0, 14, 14}, {0, 6, 8, 14} y {6, 6, 8, 8} tiene una media de 7. Sus desviaciones estándar son 7, 5, y 1, respectivamente. La tercera población tiene una desviación estándar mucho más pequeña que las otras dos porque todos sus valores están cerca de 7. Estas desviaciones estándar tienen las mismas unidades que los puntos de datos mismos. Si, por ejemplo, el conjunto de datos {0, 6, 8, 14} representa las edades de una población de cuatro hermanos en años, la desviación estándar es de 5 años. Como otro ejemplo, la población {1000, 1006, 1008, 1014} puede representar las distancias recorridas por cuatro atletas, medidas en metros. Tiene una media de 1007 metros y una desviación estándar de 5 metros.

La desviación estándar puede servir como medida de incertidumbre. En ciencia física, por ejemplo, la desviación estándar reportada de un grupo de medidas repetidas da la precisión de esas medidas. Al decidir si las mediciones concuerdan con una predicción teórica, la desviación estándar de esas mediciones es de crucial importancia: si la media de las mediciones está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces la teoría que se está probando probablemente necesita ser revisado. Esto tiene sentido ya que se encuentran fuera del rango de valores que razonablemente se podría esperar que ocurran, si la predicción fuera correcta y la desviación estándar se cuantificara apropiadamente. Ver intervalo de predicción.

Si bien la desviación estándar mide qué tan lejos tienden a estar los valores típicos de la media, hay otras medidas disponibles. Un ejemplo es la desviación absoluta media, que podría considerarse una medida más directa de la distancia media, en comparación con la raíz de la distancia cuadrática media inherente a la desviación estándar.

Ejemplos de aplicación

El valor práctico de entender la desviación estándar de un conjunto de valores está en apreciar cuánta variación hay del promedio (media).

Pruebas experimentales, industriales y de hipótesis

La desviación estándar se usa a menudo para comparar datos del mundo real con un modelo para probar el modelo. Por ejemplo, en aplicaciones industriales, es posible que el peso de los productos que salen de una línea de producción deba cumplir con un valor legalmente requerido. Pesando una fracción de los productos se puede encontrar un peso promedio, que siempre será ligeramente diferente del promedio a largo plazo. Mediante el uso de desviaciones estándar, se puede calcular un valor mínimo y máximo en el que el peso promedio estará dentro de un porcentaje muy alto del tiempo (99,9 % o más). Si cae fuera del rango, es posible que sea necesario corregir el proceso de producción. Las pruebas estadísticas como estas son particularmente importantes cuando la prueba es relativamente costosa. Por ejemplo, si es necesario abrir, drenar y pesar el producto, o si la prueba agotó el producto.

En la ciencia experimental se utiliza un modelo teórico de la realidad. La física de partículas utiliza convencionalmente un estándar de " 5 sigma " para la declaración de un descubrimiento. Un nivel de cinco sigma se traduce en una posibilidad entre 3,5 millones de que una fluctuación aleatoria produzca el resultado. Se requería este nivel de certeza para afirmar que se había descubierto una partícula consistente con el bosón de Higgs en dos experimentos independientes en el CERN, lo que también condujo a la declaración de la primera observación de ondas gravitacionales y la confirmación del calentamiento global.

Tiempo

Como ejemplo simple, considere las temperaturas máximas diarias promedio para dos ciudades, una tierra adentro y otra en la costa. Es útil entender que el rango de temperaturas máximas diarias para las ciudades cercanas a la costa es menor que para las ciudades del interior. Por lo tanto, si bien estas dos ciudades pueden tener cada una la misma temperatura máxima promedio, la desviación estándar de la temperatura máxima diaria para la ciudad costera será menor que la de la ciudad interior ya que, en cualquier día en particular, es más probable que la temperatura máxima real estar más lejos de la temperatura máxima media de la ciudad interior que de la costera.

Finanzas

En finanzas, la desviación estándar se usa a menudo como una medida del riesgo asociado con las fluctuaciones de precios de un activo determinado (acciones, bonos, propiedades, etc.), o el riesgo de una cartera de activos.(fondos mutuos administrados activamente, fondos mutuos indexados o ETF). El riesgo es un factor importante para determinar cómo administrar eficientemente una cartera de inversiones porque determina la variación en los rendimientos del activo y/o la cartera y brinda a los inversores una base matemática para las decisiones de inversión (conocida como optimización de la varianza media). El concepto fundamental del riesgo es que a medida que aumenta, el rendimiento esperado de una inversión también debe aumentar, un aumento conocido como prima de riesgo. En otras palabras, los inversores deben esperar un mayor rendimiento de una inversión cuando esa inversión conlleva un mayor nivel de riesgo o incertidumbre. Al evaluar las inversiones, los inversores deben estimar tanto el rendimiento esperado como la incertidumbre de los rendimientos futuros. La desviación estándar proporciona una estimación cuantificada de la incertidumbre de los rendimientos futuros.

Por ejemplo, suponga que un inversionista tuvo que elegir entre dos acciones. La acción A durante los últimos 20 años tuvo un rendimiento promedio del 10 por ciento, con una desviación estándar de 20 puntos porcentuales (pp) y la acción B, durante el mismo período, tuvo un rendimiento promedio del 12 por ciento pero una desviación estándar más alta de 30 pp. Sobre la base del riesgo y el rendimiento, un inversor puede decidir que la acción A es la opción más segura, porque los dos puntos porcentuales adicionales de rendimiento de la acción B no valen la desviación estándar adicional de 10 pp (mayor riesgo o incertidumbre del rendimiento esperado). Es probable que la acción B no alcance la inversión inicial (pero también supere la inversión inicial) con más frecuencia que la acción A en las mismas circunstancias, y se estima que rinde solo un dos por ciento más en promedio. En este ejemplo, se espera que la acción A gane alrededor del 10 por ciento, más o menos 20 pp (un rango de 30 por ciento a −10 por ciento), aproximadamente dos tercios de los rendimientos del año futuro. Al considerar rendimientos o resultados posibles más extremos en el futuro, un inversor debe esperar resultados de hasta un 10 por ciento más o menos 60 pp, o un rango de 70 por ciento a −50 por ciento, que incluye resultados para tres desviaciones estándar del rendimiento promedio. (alrededor del 99,7 por ciento de los rendimientos probables).

Calcular el promedio (o la media aritmética) del rendimiento de un valor durante un período determinado generará el rendimiento esperado del activo. Para cada período, al restar el rendimiento esperado del rendimiento real se obtiene la diferencia con respecto a la media. Al elevar al cuadrado la diferencia en cada período y tomar el promedio, se obtiene la variación general del rendimiento del activo. Cuanto mayor sea la varianza, mayor será el riesgo que conlleva la seguridad. Encontrar la raíz cuadrada de esta varianza dará la desviación estándar de la herramienta de inversión en cuestión.

La desviación estándar de la población se utiliza para establecer el ancho de las Bandas de Bollinger, una herramienta de análisis técnico. Por ejemplo, la Banda de Bollinger superior se da como ${displaystyle textstyle {bar {x}}+nsigma _{x}.}$ El valor más utilizado para n es 2; hay alrededor de un cinco por ciento de posibilidades de salir, suponiendo una distribución normal de rendimientos.

Se sabe que las series de tiempo financieras son series no estacionarias, mientras que los cálculos estadísticos anteriores, como la desviación estándar, se aplican solo a las series estacionarias. Para aplicar las herramientas estadísticas anteriores a series no estacionarias, la serie primero debe transformarse en una serie estacionaria, lo que permite el uso de herramientas estadísticas que ahora tienen una base válida para trabajar.

Interpretación geométrica

Para obtener algunas ideas y aclaraciones geométricas, comenzaremos con una población de tres valores, x ₁, x ₂, x ₃. Esto define un punto P = (x ₁, x ₂, x ₃) en R. Considere la línea L = {(r, r, r): r ∈ R }. Esta es la "diagonal principal" que pasa por el origen. Si nuestros tres valores dados fueran todos iguales, entonces la desviación estándar sería cero y P estaría en L. Entonces, no es irrazonable suponer que la desviación estándar está relacionada con la distancia de P a L. Ese es de hecho el caso. Para moverse ortogonalmente desde L hasta el punto P, se comienza en el punto: ${displaystyle M=left({bar {x}},{bar {x}},{bar {x}}right)}$

cuyas coordenadas son la media de los valores con los que comenzamos.

Un poco de álgebra muestra que la distancia entre P y M (que es igual a la distancia ortogonal entre P y la línea L) ${textstyle {sqrt {sum _{i}left(x_{i}-{bar {x}}right)^{2}}}}$ es igual a la desviación estándar del vector (x ₁, x ₂, x ₃), multiplicada por la raíz cuadrada del número de dimensiones del vector (3 en este caso).

Desigualdad de Chebyshev

Una observación rara vez está a más de unas pocas desviaciones estándar de la media. La desigualdad de Chebyshev asegura que, para todas las distribuciones para las que se define la desviación estándar, la cantidad de datos dentro de un número de desviaciones estándar de la media es al menos tanto como se indica en la siguiente tabla.

{ estilo de visualización { sqrt {2}} , sigma}

Distancia desde la media	Población mínima
${ estilo de visualización { sqrt {2}} , sigma}$	50%
2 σ	75%
3 σ	89%
4 σ	94%
5 σ	96%
6 σ	97%
$ksigma$	${displaystyle 1-{frac{1}{k^{2}}}}$
${displaystyle {frac {1}{sqrt {1-ell }}},sigma }$	$ana$

Reglas para datos normalmente distribuidos

El teorema del límite central establece que la distribución de un promedio de muchas variables aleatorias independientes distribuidas de manera idéntica tiende hacia la famosa distribución normal en forma de campana con una función de densidad de probabilidad de ${displaystyle fleft(x,mu,sigma ^{2}right)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac { 1}{2}}left({frac {x-mu }{sigma}}right)^{2}}}$

donde μ es el valor esperado de las variables aleatorias, σ es igual a la desviación estándar de su distribución dividida por n y n es el número de variables aleatorias. Por lo tanto, la desviación estándar es simplemente una variable de escala que ajusta la amplitud de la curva, aunque también aparece en la constante de normalización.

Si una distribución de datos es aproximadamente normal, entonces la proporción de valores de datos dentro de z desviaciones estándar de la media se define por: ${displaystyle {text{Proporción}}=operatorname {erf} left({frac {z}{sqrt {2}}}right)}$

donde ${ estilo de visualización estilo de texto nombre del operador {erf}}$ está la función de error. La proporción que es menor o igual a un número, x, viene dada por la función de distribución acumulativa: ${displaystyle {text{Proporción}}leq x={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma { sqrt {2}}}}right)right]={frac {1}{2}}left[1+operatorname {erf} left({frac {z}{sqrt {2} }}bien bien]}$ .

Si una distribución de datos es aproximadamente normal, alrededor del 68 por ciento de los valores de los datos están dentro de una desviación estándar de la media (matemáticamente, μ ± σ, donde μ es la media aritmética), alrededor del 95 por ciento están dentro de dos desviaciones estándar (μ ± 2 σ), y alrededor del 99,7 por ciento se encuentran dentro de tres desviaciones estándar (μ ± 3 σ). Esto se conoce como la regla 68–95–99.7 o la regla empírica.

Para varios valores de z, el porcentaje de valores que se espera que estén dentro y fuera del intervalo simétrico, CI = (− zσ, zσ), son los siguientes:

Intervalo de confianza	proporción dentro	proporción sin
Porcentaje	Porcentaje	Fracción
0.318 639 σ	25%	75%	3 / 4
0.674 490 σ	50 %	50 %	1 / 2
0.977 925 σ	66.6667%	33.3333%	1 / 3
0.994 458 σ	68%	32%	1 / 3.125
1 σ	68.268 9492 %	31.731 0508 %	1 / 3.151 4872
1.281 552 σ	80%	20%	15
1.644 854 σ	90%	10%	1 / 10
1.959 964 σ	95%	5%	1 / 20
2 σ	95.449 9736 %	4.550 0264 %	1 / 21.977 895
2.575 829 σ	99%	1%	1 / 100
3 σ	99.730 0204 %	0,269 9796 %	1 / 370.398
3.290 527 σ	99,9%	0,1%	1 / 1000
3.890 592 σ	99,99%	0.01%	1 / 10 000
4 σ	99.993 666 %	0,006 334 %	1 / 15 787
4.417 173 σ	99.999%	0.001%	1 / 100 000
4.5 σ	99.999 320 465 3751%	0.000 679 534 6249%	1 / 147 159.53586.8 / 1 000 000
4.891 638 σ	99,9999 %	0,0001 %	1 / 1 000 000
5 σ	99.999 942 6697 %	0.000 057 3303 %	1 / 1 744 278
5.326 724 σ	99.999 99 %	0.000 01 %	1 / 10 000 000
5.730 729 σ	99.999 999 %	0.000 001 %	1 / 100 000 000
6 σ	99.999 999 8027 %	0.000 000 1973 %	1 / 506 797 346
6.109 410 σ	99.999 9999 %	0.000 0001 %	1 / 1 000 000 000
6.466 951 σ	99.999 999 99 %	0.000 000 01 %	1 / 10 000 000 000
6.806 502 σ	99.999 999 999 %	0.000 000 001 %	1 / 100 000 000 000
7 σ	99.999 999 999 7440%	0.000 000 000 256 %	1 / 390 682 215 445

Relación entre la desviación estándar y la media

La media y la desviación estándar de un conjunto de datos son estadísticas descriptivas que generalmente se informan juntas. En cierto sentido, la desviación estándar es una medida "natural" de dispersión estadística si el centro de los datos se mide con respecto a la media. Esto se debe a que la desviación estándar de la media es menor que la de cualquier otro punto. El enunciado preciso es el siguiente: supongamos que x ₁,..., x _n son números reales y definen la función: ${displaystyle sigma (r)={sqrt {{frac {1}{N-1}}sum _{i=1}^{N}left(x_{i}-rright)^ {2}}}.}$

Usando cálculo o completando el cuadrado, es posible mostrar que σ (r) tiene un único mínimo en la media: ${displaystyle r={bar {x}}.,}$

La variabilidad también se puede medir por el coeficiente de variación, que es la relación entre la desviación estándar y la media. Es un número adimensional.

Desviación estándar de la media

A menudo, queremos alguna información sobre la precisión de la media que obtuvimos. Podemos obtener esto determinando la desviación estándar de la media muestreada. Suponiendo independencia estadística de los valores de la muestra, la desviación estándar de la media está relacionada con la desviación estándar de la distribución por: ${displaystyle sigma_{text{media}}={frac {1}{sqrt {N}}}sigma}$

donde N es el número de observaciones en la muestra utilizada para estimar la media. Esto se puede probar fácilmente con (ver propiedades básicas de la varianza): ${displaystyle {begin{alineado}operatorname {var} (X)&equiv sigma _{X}^{2}\operatorname {var} (X_{1}+X_{2})& equiv nombre de operador {var} (X_{1})+nombre de operador {var} (X_{2})\end{alineado}}}$

(Se supone independencia estadística.) ${displaystyle nombre del operador {var} (cX_{1})equiv c^{2},nombre del operador {var} (X_{1})}$

por lo tanto ${displaystyle {begin{alineado}operatorname {var} ({text{mean}})&=operatorname {var} left({frac {1}{N}}sum _{i=1 }^{N}X_{i}right)={frac {1}{N^{2}}}nombre del operador {var} left(sum_{i=1}^{N}X_{i }right)\&={frac {1}{N^{2}}}sum _{i=1}^{N}operatorname {var} (X_{i})={frac { N}{N^{2}}}nombre de operador {var} (X)={frac {1}{N}}nombre de operador {var} (X).end{alineado}}}$

Resultando en: $sigma _{text{media}}={frac {sigma }{sqrt {N}}}.$

Para estimar la desviación estándar de la media es necesario conocer de antemano $sigma _{text{media}}$ la desviación estándar de toda la población. $sigma$ Sin embargo, en la mayoría de las aplicaciones este parámetro es desconocido. Por ejemplo, si en un laboratorio se realiza una serie de 10 mediciones de una cantidad previamente desconocida, es posible calcular la media de la muestra resultante y la desviación estándar de la muestra, pero es imposible calcular la desviación estándar de la media.

Métodos de cálculo rápido

Las siguientes dos fórmulas pueden representar una desviación estándar continua (actualizada repetidamente). Se calcula un conjunto de dos sumas de potencias s ₁ y s _{2 sobre un conjunto de}N valores de x, indicados como x ₁,..., x _N: ${displaystyle s_{j}=sum _{k=1}^{N}{x_{k}^{j}}.}$

Dados los resultados de estas sumas en ejecución, los valores N, s ₁, s ₂ se pueden usar en cualquier momento para calcular el valor actual de la desviación estándar en ejecución: ${displaystyle sigma ={frac {sqrt {Ns_{2}-s_{1}^{2}}}{N}}}$

Donde N, como se mencionó anteriormente, es el tamaño del conjunto de valores (o también puede considerarse como s ₀).

De manera similar para la desviación estándar de la muestra, ${displaystyle s={sqrt {frac {Ns_{2}-s_{1}^{2}}{N(N-1)}}}.}$

En una implementación por computadora, a medida que las dos sumas s _j se vuelven grandes, debemos considerar el error de redondeo, el desbordamiento aritmético y el subdesbordamiento aritmético. El siguiente método calcula el método de sumas acumulativas con errores de redondeo reducidos. Este es un algoritmo de "una pasada" para calcular la varianza de n muestras sin necesidad de almacenar datos previos durante el cálculo. La aplicación de este método a una serie temporal dará como resultado valores sucesivos de desviación estándar correspondientes a n puntos de datos a medida que n crece con cada nueva muestra, en lugar de un cálculo de ventana deslizante de ancho constante.

Para k = 1,..., n: ${displaystyle {begin{alineado}A_{0}&=0\A_{k}&=A_{k-1}+{frac {x_{k}-A_{k-1}}{k} }end{alineado}}}$

donde A es el valor medio. ${displaystyle {begin{alineado}Q_{0}&=0\Q_{k}&=Q_{k-1}+{frac {k-1}{k}}left(x_{k} -A_{k-1}right)^{2}=Q_{k-1}+left(x_{k}-A_{k-1}right)left(x_{k}-A_{k }right)end{alineado}}}$

Nota: $Q_{1}=0$ desde $k-1=0$ o $x_{1}=A_{1}$

Variación de la muestra: ${displaystyle s_{n}^{2}={frac {Q_{n}}{n-1}}}$

Varianza de la población: ${displaystyle sigma _{n}^{2}={frac {Q_{n}}{n}}}$

Cálculo ponderado

Cuando los valores x _i se ponderan con pesos desiguales w _i, las sumas de potencias s ₀, s ₁, s ₂ se calculan como: ${displaystyle s_{j}=sum _{k=1}^{N}w_{k}x_{k}^{j}.,}$

Y las ecuaciones de desviación estándar permanecen sin cambios. s ₀ es ahora la suma de los pesos y no el número de muestras N.

También se puede aplicar el método incremental con errores de redondeo reducidos, con cierta complejidad adicional.

Se debe calcular una suma acumulada de pesos para cada k de 1 a n: ${displaystyle {begin{alineado}W_{0}&=0\W_{k}&=W_{k-1}+w_{k}end{alineado}}}$

y los lugares donde se usa 1/ n arriba deben ser reemplazados por w _i / W _n: ${displaystyle {begin{alineado}A_{0}&=0\A_{k}&=A_{k-1}+{frac {w_{k}}{W_{k}}}left(x_{k}-A_{k-1}right)\Q_{0}&=0\Q_{k}&=Q_{k-1}+{frac {w_{k}W_{k- 1}}{W_{k}}}left(x_{k}-A_{k-1}right)^{2}=Q_{k-1}+w_{k}left(x_{k} -A_{k-1}right)left(x_{k}-A_{k}right)end{alineado}}}$

En la división final, ${displaystyle sigma _{n}^{2}={frac {Q_{n}}{W_{n}}},}$

y ${displaystyle s_{n}^{2}={frac {Q_{n}}{W_{n}-1}},}$

o ${displaystyle s_{n}^{2}={frac {n'}{n'-1}}sigma _{n}^{2},}$

donde n es el número total de elementos y n' es el número de elementos con pesos distintos de cero.

Las fórmulas anteriores se vuelven iguales a las fórmulas más simples dadas anteriormente si los pesos se toman como iguales a uno.

Historia

El término desviación estándar fue utilizado por primera vez por escrito por Karl Pearson en 1894, luego de su uso en conferencias. Esto fue como un reemplazo de los nombres alternativos anteriores para la misma idea: por ejemplo, Gauss usó error medio.