Curva de contrato

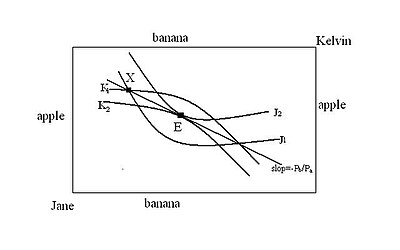
En microeconomía, la curva de contrato o el conjunto de Pareto es el conjunto de puntos que representan las asignaciones finales de dos bienes entre dos personas que podrían ocurrir como resultado de un intercambio mutuamente beneficioso. entre esas personas dada su asignación inicial de bienes. Todos los puntos en este locus son asignaciones eficientes de Pareto, lo que significa que desde cualquiera de estos puntos no hay reasignación que pueda hacer que una de las personas esté más satisfecha con su asignación sin que la otra persona esté menos satisfecha. La curva de contrato es el subconjunto de los puntos eficientes de Pareto que podrían alcanzarse comerciando con las tenencias iniciales de los dos bienes por parte de la gente. Se dibuja en el diagrama de caja de Edgeworth que se muestra aquí, en el que la asignación de cada persona se mide verticalmente para un bien y horizontalmente para el otro bien del origen de esa persona (punto de asignación cero de ambos bienes); El origen de una persona es la esquina inferior izquierda del cuadro de Edgeworth y el origen de la otra persona es la esquina superior derecha del cuadro. Las dotaciones iniciales de la gente (asignaciones iniciales de los dos bienes) están representadas por un punto en el diagrama; las dos personas intercambiarán bienes entre sí hasta que ya no sea posible realizar más intercambios mutuamente beneficiosos. El conjunto de puntos en los que conceptualmente les es posible detenerse son los puntos de la curva del contrato.

Sin embargo, la mayoría de los autores identifican la curva de contrato como el locus eficiente de Pareto completo de un origen al otro.

Cualquier equilibrio walrasiano se encuentra en la curva del contrato. Como ocurre con todos los puntos que son eficientes en Pareto, cada punto de la curva de contrato es un punto de tangencia entre una curva de indiferencia de una persona y una curva de indiferencia de la otra. Por tanto, en la curva de contrato la tasa marginal de sustitución es la misma para ambas personas.

Ejemplo

Supongamos la existencia de una economía con dos agentes, Octavio y Abby, que consumen dos bienes X e Y de los cuales hay oferta fija, como se ilustra en el diagrama de caja de Edgeworth anterior. Además, supongamos una distribución inicial (dotación) de los bienes entre Octavio y Abby y supongamos que cada uno tenga preferencias normalmente estructuradas (convexas) representadas por curvas de indiferencia que son convexas hacia los respectivos orígenes de las personas. Si la asignación inicial no está en un punto de tangencia entre una curva de indiferencia de Octavio y una de Abby, entonces esa asignación inicial debe estar en un punto donde una curva de indiferencia de Octavio cruza una de Abby. Estas dos curvas de indiferencia forman una lente, con la asignación inicial en una de las dos esquinas de la lente. Octavio y Abby optarán por realizar intercambios mutuamente beneficiosos, es decir, negociarán hasta un punto que se encuentre en una curva de indiferencia mejor (más alejada del origen) para ambos. Dicho punto estará en el interior de la lente, y la tasa a la que se intercambiará un bien por otro estará entre la tasa marginal de sustitución de Octavio y la de Abby. Dado que las transacciones siempre proporcionarán a cada persona más de un bien y menos del otro, el comercio da como resultado un movimiento hacia arriba y hacia la izquierda, o hacia abajo y hacia la derecha, en el diagrama.

Las dos personas continuarán comerciando mientras la tasa marginal de sustitución de cada una (el valor absoluto de la pendiente de la curva de indiferencia de la persona en ese punto) difiera de la de la otra persona. en la asignación actual (en cuyo caso habrá una relación mutuamente aceptable de intercambio de un bien por otro, entre las diferentes tasas marginales de sustitución). En un punto en el que la tasa marginal de sustitución de Octavio es igual a la tasa marginal de sustitución de Abby, no es posible un intercambio más mutuamente beneficioso. Este punto se llama equilibrio eficiente de Pareto. En el cuadro de Edgeworth, es un punto en el que la curva de indiferencia de Octavio es tangente a la curva de indiferencia de Abby, y está dentro de la lente formada por sus asignaciones iniciales.

Así, la curva de contrato, el conjunto de puntos en los que Octavio y Abby podrían terminar, es la sección del lugar eficiente de Pareto que está en el interior de la lente formada por las asignaciones iniciales. El análisis no puede decir en qué punto particular de la curva del contrato terminarán; esto depende de las habilidades de negociación de las dos personas.

Explicación matemática

En el caso de dos mercancías y dos personas, la curva del contrato se puede encontrar como sigue. Aquí. ${displaystyle #$ se refiere a la cantidad final de la buena 2 asignada a la persona 1, etc., ${displaystyle u^{1}$ y ${displaystyle u^{2}$ referencia a los niveles finales de utilidad experimentados por persona 1 y persona 2 respectivamente, ${displaystyle U_{0} {2}$ se refiere al nivel de utilidad que la persona 2 recibiría de la asignación inicial sin negociar en absoluto, y ${displaystyle omega _{1} {tot}}$ y ${displaystyle omega _{2} {tot}}$ se refieren a las cantidades totales fijas disponibles de las mercancías 1 y 2 respectivamente.

${displaystyle max ¿Qué?$

sujeto a:

${displaystyle x_{1}{1}+x_{1}{2}leq omega _{1}^{tot}}$

${displaystyle x_{2}{1}+x_{2}leq omega _{2}^{tot}}$

${displaystyle u^{2}(x_{1}{2},x_{2}}geq U_{0} {2}$

Este problema de optimización establece que los bienes deben asignarse entre las dos personas de tal manera que no se asigne a las dos personas combinadas más de la cantidad disponible de cada bien, y la utilidad de la primera persona es ser lo más alto posible y al mismo tiempo hacer que la utilidad de la segunda persona no sea menor que en la asignación inicial (para que la segunda persona no se niegue a comerciar desde la asignación inicial hasta el punto encontrado); esta formulación del problema encuentra un punto eficiente de Pareto en la lente, lo más lejos posible del origen de la persona. Este es el punto que se alcanzaría si la persona 1 tuviera todo el poder de negociación. (De hecho, para crear al menos un ligero incentivo para que la persona 2 acepte comerciar hasta el punto identificado, el punto tendría que estar ligeramente dentro de la lente).

Para trazar toda la curva del contrato, el problema de optimización anterior se puede modificar de la siguiente manera. Maximizar un promedio ponderado de las utilidades de las personas 1 y 2, con pesos b y 1 – b, sujeto a las restricciones de que las asignaciones de cada bien no excedan su oferta y sujeto a las restricciones de que las utilidades de ambas personas sean al menos tan grandes como sus utilidades en las dotaciones iniciales:

${displaystyle max ¿Por qué?$

sujeto a:

${displaystyle x_{1}{1}+x_{1}{2}leq omega _{1}^{tot}}$

${displaystyle x_{2}{1}+x_{2}leq omega _{2}^{tot}}$

${displaystyle u^{1}(x_{1}{1},x_{2}{1})geq U_{0} {1}$

${displaystyle u^{2}(x_{1}{2},x_{2}}geq U_{0} {2}$

Donde ${displaystyle u^{1}$ es la utilidad que la persona 1 experimentaría en ausencia de comercio lejos de la dotación inicial. Variando el parámetro de ponderación b, se puede rastrear toda la curva del contrato: Si b = 1 el problema es el mismo que el problema anterior, e identifica un punto eficiente en un borde del objetivo formado por las curvas de indiferencia de la dotación inicial; si b = 0 todo el peso está en la utilidad de la persona 2 en lugar de la persona 1's, y por lo tanto la optimización identifica el punto eficiente en el otro borde de la lente. As b varía suavemente entre estos dos extremos, todos los puntos entre la curva del contrato se rastrean.

Tenga en cuenta que las optimizaciones anteriores no son aquellas en las que las dos personas realmente participarían, ya sea explícita o implícitamente. Más bien, estas optimizaciones son simplemente una forma que tiene el economista de identificar puntos en la curva del contrato.