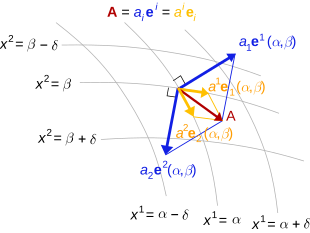
Covarianza y contravarianza de vectores

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Manner en el que un objeto geométrico varía con un cambio de base

A vector, v, representado en términos de

base tangente: e₁, e₂, e₃ a la curvas de coordenadas (izquierda),
base dual, base covectoral o base recíproca: e¹, e², e³ a superficies de coordenadas (derecho),

en general coordenadas curvilinear ()q¹, q², q³), un tuple de números para definir un punto en un espacio de posición. Tenga en cuenta que la base y la cobasis coinciden sólo cuando la base es ortogonal.

En física, especialmente en álgebra multilineal y análisis tensorial, la covarianza y la contravarianza describen cómo cambia la descripción cuantitativa de ciertas entidades geométricas o físicas con un cambio de base. En la notación matemática moderna, a veces se intercambia el papel.

En física, a veces se considera que una base es un conjunto de ejes de referencia. Un cambio de escala en los ejes de referencia corresponde a un cambio de unidades en el problema. Por ejemplo, cambiando la escala de metros a centímetros (es decir, dividiendo la escala de los ejes de referencia por 100), los componentes de un vector de velocidad medido se multiplican por 100 Un vector cambia de escala inversamente a los cambios de escala en los ejes de referencia, y en consecuencia se llama contravariante. Como resultado, un vector a menudo tiene unidades de distancia o distancia con otras unidades (por ejemplo, la velocidad tiene unidades de distancia divididas por tiempo).

Por el contrario, un covector, también llamado vector dual, normalmente tiene unidades del inverso de la distancia o el inverso de la distancia con otras unidades. Por ejemplo, un degradado tiene unidades de derivada espacial o distancia⁻¹. Las componentes de un covector cambian de la misma manera que los cambios de escala de los ejes de referencia, por lo que se denomina covariante.

Un tercer concepto relacionado con la covarianza y la contravarianza es la invariancia. Un ejemplo de un observable físico que no cambia con un cambio de escala en los ejes de referencia es la masa de una partícula, que tiene unidades de masa (es decir, no tiene unidades de distancia). El único valor escalar de la masa es independiente de los cambios en la escala de los ejes de referencia y, en consecuencia, se denomina invariante.

Bajo cambios más generales en la base:

Un vector contravariante o vector tangente (a menudo abreviado simplemente como vector, como un vector de dirección o vector de velocidad) tiene componentes que contra-vary con un cambio de base para compensar. Es decir, la matriz que transforma los componentes vectoriales debe ser el inverso de la matriz que transforma los vectores base. Se dice que los componentes de los vectores (a diferencia de los de los covectores) son contravariante. Ejemplos de vectores con componentes contravariantes incluir la posición de un objeto relativo a un observador, o cualquier derivado de la posición con respecto al tiempo, incluyendo velocidad, aceleración y tirón. En la notación de Einstein (summación implícita sobre índice repetido), los componentes contravariantes se denotan con índices superiores como en
${displaystyle mathbf {v} =v^{i}mathbf {e} _{i}}$
Un vector covariante o vector cotangente (a menudo abreviado como covector) tiene componentes que co-vary con un cambio de base. Es decir, los componentes deben ser transformados por la misma matriz que el cambio de matriz base. Se dice que los componentes de los covectores (a diferencia de los vectores) son covariante. Ejemplos de vectores covariantes generalmente aparecen al tomar un gradiente de una función. En la notación de Einstein, los componentes covariantes se denotan con índices inferiores como en
${displaystyle mathbf {w} =w_{i}mathbf {e} ^{i}.}$

Los sistemas de coordenadas curvilíneas, como las coordenadas cilíndricas o esféricas, se usan a menudo en problemas físicos y geométricos. Asociado con cualquier sistema de coordenadas hay una elección natural de base de coordenadas para vectores basados en cada punto del espacio, y la covarianza y la contravarianza son particularmente importantes para comprender cómo cambia la descripción de coordenadas de un vector al pasar de un sistema de coordenadas a otro.

Los términos covariante y contravariante fueron introducidos por James Joseph Sylvester en 1851 en el contexto de la teoría de formas algebraicas asociadas. Los tensores son objetos en álgebra multilineal que pueden tener aspectos tanto de covarianza como de contravarianza.

En el léxico de la teoría de categorías, la covarianza y la contravarianza son propiedades de los funtores; desafortunadamente, son los objetos de índice inferior (covectores) los que genéricamente tienen pullbacks, que son contravariantes, mientras que los objetos de índice superior (vectores) tienen pushforwards, que son covariantes. Este conflicto terminológico se puede evitar llamando a los funtores contravariantes "cofuntores" de acuerdo con el "covector" terminología.

Introducción

En física, un vector suele surgir como resultado de una medición o serie de mediciones y se representa como una lista (o tupla) de números como

{displaystyle (v_{1},v_{2},v_{3}).}

Los números en la lista dependen de la elección del sistema de coordenadas. Por ejemplo, si el vector representa la posición con respecto a un observador (vector de posición), entonces el sistema de coordenadas puede obtenerse de un sistema de varillas rígidas, o ejes de referencia, a lo largo de los cuales las componentes v₁, v₂ y v₃. Para que un vector represente un objeto geométrico, debe ser posible describir cómo se ve en cualquier otro sistema de coordenadas. Es decir, las componentes de los vectores se transformarán de cierta forma al pasar de un sistema de coordenadas a otro.

A contravariante vector tiene componentes que "transforman como lo hacen las coordenadas" bajo cambios de coordenadas (y así inversamente a la transformación de los ejes de referencia), incluyendo rotación y dilatación. El vector en sí no cambia bajo estas operaciones; en cambio, los componentes del vector cambian de una manera que cancela el cambio en los ejes espaciales, de la misma manera que coordina el cambio. En otras palabras, si los ejes de referencia se rotaban en una dirección, la representación componente del vector giraría exactamente de la manera opuesta. Del mismo modo, si los ejes de referencia se estiraban en una dirección, los componentes del vector, como las coordenadas, reducirían de manera exactamente compensadora. Matemáticamente, si el sistema de coordenadas sufre una transformación descrita por una matriz invertible M, así que un vector de coordenadas x se transforma en ${displaystyle mathbf {x} '=Mmathbf {x} }$ , entonces un vector contravariante v debe ser transformado de forma similar ${displaystyle mathbf {v} '=Mmathbf {v} }$ . Este requisito importante es lo que distingue un vector contravariante de cualquier otro triple de cantidades físicamente significativas. Por ejemplo, si v consiste en x- Sí.- y z-componentes de velocidad, entonces v es un vector contravariante: si las coordenadas del espacio son estiradas, rotadas o retorcidas, entonces los componentes de la velocidad se transforman de la misma manera. Ejemplos de vectores contravariantes incluyen posición, desplazamiento, velocidad, aceleración, impulso y fuerza.

Por el contrario, un vector covariante tiene componentes que cambian de forma opuesta a las coordenadas o, de manera equivalente, se transforman como los ejes de referencia. Por ejemplo, las componentes del vector gradiente de una función

nabla f = frac{partial f}{partial x^1}widehat{x}^1+frac{partial f}{partial x^2}widehat{x}^2+frac{partial f}{partial x^3}widehat{x}^3

se transforman como los propios ejes de referencia.

Definición

Componentes covariantes y contravariantes de un vector cuando la base no es ortogonal.

La formulación general de covarianza y contravarianza se refiere a cómo los componentes de un vector de coordenadas se transforman bajo un cambio de base (transformación pasiva). Así, sea V un espacio vectorial de dimensión n sobre un campo de escalares S, y sea cada uno de f = (X₁,..., X_n) y f′ = (Y₁,..., Y_n) ser una base de V. Además, sea el cambio de base de f a f′ dado por

mathbf{f}mapsto mathbf{f}' = left(sum_i a^i_1X_i,dots,sum_i a^i_nX_iright) = mathbf{f}A

()1)

para algunos invertidos n×n matriz A con entradas $a^i_j$ . Aquí, cada vector Y_j de la f′ base es una combinación lineal de los vectores X_i de la f base, para que

Y_j=sum_i a^i_jX_i.

Transformación contravariante

Un vector $v$ dentro V se expresa singularmente como una combinación lineal de los elementos $X_{i}$ de la f base

{displaystyle v=sum _{i}v^{i}[mathbf {f} ]X_{i},}

()2)

donde vⁱ[f ] son elementos del campo S conocidos como los componentes de v en la base f. Denote el vector columna de los componentes de v por v[f]:

mathbf{v}[mathbf{f}] = begin{bmatrix}v^1[mathbf{f}]\v^2[mathbf{f}]\vdots\v^n[mathbf{f}]end{bmatrix}

para que (2) se pueda reescribir como un producto de matriz

v = mathbf{f}, mathbf{v}[mathbf{f}].

El vector v también se puede expresar en términos de la base f′, de modo que

v = mathbf{f'}, mathbf{v}[mathbf{f'}].

Sin embargo, dado que el vector v en sí mismo es invariante bajo la elección de la base,

mathbf{f}, mathbf{v}[mathbf{f}] = v = mathbf{f'}, mathbf{v}[mathbf{f'}].

La invariancia de v combinada con la relación (1) entre f y f′ implica que

mathbf{f}, mathbf{v}[mathbf{f}] = mathbf{f}A, mathbf{v}[mathbf{f}A],

dando la regla de transformación

{displaystyle mathbf {v} [mathbf {f'} ]=mathbf {v} [mathbf {f} A]=A^{-1}mathbf {v} [mathbf {f} ].}

En términos de componentes,

v^i[mathbf{f}A] = sum_j tilde{a}^i_jv^j[mathbf{f}]

donde los coeficientes $tilde{a}^i_j$ son las entradas de la matriz inversa de A.

Debido a que las componentes del vector v se transforman con la inversa de la matriz A, se dice que estas componentes se transforman contravariantemente bajo un cambio de base.

La forma en que A relaciona los dos pares se representa en el siguiente diagrama informal usando una flecha. La inversión de la flecha indica un cambio contravariante:

{displaystyle {begin{aligned}mathbf {f} &longrightarrow mathbf {f'} \v[mathbf {f} ]&longleftarrow v[mathbf {f'} ]end{aligned}}}

Transformación covariante

Un funcional lineal α en V se expresa únicamente en términos de sus componentes (elementos en S) en la base f como

alpha(X_i) = alpha_i[mathbf{f}] quad i=1,2,dots,n.

Estas componentes son la acción de α sobre los vectores de base X_i de la f base.

Bajo el cambio de base de f a f′ (a través de 1), los componentes se transforman de modo que

{displaystyle {begin{aligned}alpha _{i}[mathbf {f} A]&=alpha (Y_{i})\&=alpha left(sum _{j}a_{i}^{j}X_{j}right)\&=sum _{j}a_{i}^{j}alpha (X_{j})\&=sum _{j}a_{i}^{j}alpha _{j}[mathbf {f} ].end{aligned}}}

()3)

Denote el vector fila de componentes de α por α[f]:

mathbf{alpha}[mathbf{f}] = begin{bmatrix}alpha_1[mathbf{f}],alpha_2[mathbf{f}],dots,alpha_n[mathbf{f}]end{bmatrix}

para que (3) se pueda reescribir como el producto de matrices

alpha[mathbf{f}A] = alpha[mathbf{f}]A.

Debido a que los componentes del funcional lineal α se transforman con la matriz A, se dice que estos componentes se transforman covariantemente bajo un cambio de base.

La forma en que A relaciona los dos pares se representa en el siguiente diagrama informal usando una flecha. Se indica una relación covariante ya que las flechas viajan en la misma dirección:

{displaystyle {begin{aligned}mathbf {f} &longrightarrow mathbf {f'} \alpha [mathbf {f} ]&longrightarrow alpha [mathbf {f'} ]end{aligned}}}

Si en su lugar se hubiera utilizado una representación de vector de columna, la ley de transformación sería la transpuesta

alpha^mathrm{T}[mathbf{f}A] = A^mathrm{T}alpha^mathrm{T}[mathbf{f}].

Coordenadas

La elección de la base f sobre el espacio vectorial V define de forma única un conjunto de funciones de coordenadas sobre V, mediante

x^i[mathbf{f}](v) = v^i[mathbf{f}].

Las coordenadas en V son por lo tanto contravariantes en el sentido de que

x^i[mathbf{f}A] = sum_{k=1}^n tilde{a}^i_kx^k[mathbf{f}].

Por el contrario, un sistema de n cantidades vⁱ que se transforman como las coordenadas xⁱ en V define un vector contravariante. Un sistema de n cantidades que se transforman en sentido opuesto a las coordenadas es entonces un vector covariante.

Esta formulación de contravarianza y covarianza suele ser más natural en aplicaciones en las que hay un espacio de coordenadas (una variedad) en el que los vectores viven como vectores tangentes o cotangentes. Dado un sistema de coordenadas local xⁱ en la variedad, los ejes de referencia para el sistema de coordenadas son los campos vectoriales

X_1 = frac{partial}{partial x^1},dots,X_n=frac{partial}{partial x^n}.

Esto da lugar al cuadro f = (X₁,..., X_n) en cada punto del parche de coordenadas.

Si yⁱ es un sistema de coordenadas diferente y

{displaystyle Y_{1}={frac {partial }{partial y^{1}}},dotsY_{n}={frac {partial }{partial y^{n}}},}

entonces el marco f' está relacionado con el marco f por la inversa de la matriz jacobiana de la transición de coordenadas:

{displaystyle mathbf {f} '=mathbf {f} J^{-1},quad J=left({frac {partial y^{i}}{partial x^{j}}}right)_{i,j=1}^{n}.}

O, en índices,

frac{partial}{partial y^i} = sum_{j=1}^nfrac{partial x^j}{partial y^i}frac{partial}{partial x^j}.

Un vector tangente es por definición un vector que es una combinación lineal de las parciales de coordenadas $partial/partial x^i$ . Así un vector tangente se define por

v = sum_{i=1}^n v^i[mathbf{f}] X_i = mathbf{f} mathbf{v}[mathbf{f}].

Tal vector es contravariante con respecto al cambio de marco. Bajo cambios en el sistema de coordenadas, uno tiene

{displaystyle mathbf {v} left[mathbf {f} 'right]=mathbf {v} left[mathbf {f} J^{-1}right]=J,mathbf {v} [mathbf {f} ].}

Por lo tanto, las componentes de un vector tangente se transforman a través de

{displaystyle v^{i}left[mathbf {f} 'right]=sum _{j=1}^{n}{frac {partial y^{i}}{partial x^{j}}}v^{j}[mathbf {f} ].}

En consecuencia, un sistema de n cantidades vⁱ en función de las coordenadas que así se transforman en pasar de un sistema de coordenadas a otro se llama vector contravariante.

Componentes covariantes y contravariantes de un vector con una métrica

Los componentes contravariantes de un vector se obtienen proyectando sobre los ejes de coordenadas. Los componentes covariantes se obtienen proyectando sobre las líneas normales a los hiperplanos de coordenadas.

En un espacio vectorial de dimensión finita V sobre un campo K con forma bilineal simétrica g: V × V → K (que puede denominarse tensor métrico), hay poca distinción entre covariante y vectores contravariantes, porque la forma bilineal permite identificar covectores con vectores. Es decir, un vector v determina únicamente un covector α a través de

alpha(w) = g(v, w)

para todos los vectores w. Por el contrario, cada covector α determina un único vector v mediante esta ecuación. Debido a esta identificación de vectores con covectores, se puede hablar de las componentes covariantes o componentes contravariantes de un vector, es decir, no son más que representaciones del mismo vector utilizando el base recíproca.

Dada una base f = (X₁,..., X_n) de V, existe una única base recíproca f^# = (Y¹,..., Yⁿ) de V determinada al requerir que

Y^i(X_j) = delta^i_j,

el delta de Kronecker. En términos de estas bases, cualquier vector v se puede escribir de dos formas:

begin{align} v &= sum_i v^i[mathbf{f}]X_i = mathbf{f},mathbf{v}[mathbf{f}]\ &=sum_i v_i[mathbf{f}]Y^i = mathbf{f}^sharpmathbf{v}^sharp[mathbf{f}]. end{align}

Los componentes vⁱ[f] son los componentes contravariantes de el vector v en la base f, y las componentes v_i[f] son los componentes covariantes de v en la base f. La terminología se justifica porque bajo un cambio de base,

mathbf{v}[mathbf{f}A] = A^{-1}mathbf{v}[mathbf{f}],quad mathbf{v}^sharp[mathbf{f}A] = A^Tmathbf{v}^sharp[mathbf{f}].

Plano euclidiano

En el plano Euclidean, el producto punto permite identificar vectores con covectores. Si $mathbf{e}_1,mathbf{e}_2$ es una base, entonces la base dual $mathbf{e}^1,mathbf{e}^2$ satisfizo

{displaystyle {begin{aligned}mathbf {e} ^{1}cdot mathbf {e} _{1}=1,&quad mathbf {e} ^{1}cdot mathbf {e} _{2}=0\mathbf {e} ^{2}cdot mathbf {e} _{1}=0,&quad mathbf {e} ^{2}cdot mathbf {e} _{2}=1.end{aligned}}}

Así, e¹ y e₂ son perpendiculares entre sí, al igual que e ² y e₁, y las longitudes de e¹ y e² normalizados frente a e₁ y e₂, respectivamente.

Ejemplo

Por ejemplo, supongamos que se nos da una base e₁, e₂ que consiste en un par de vectores que forman un ángulo de 45° entre sí, tales que e₁ tiene longitud 2 y e₂ tiene longitud 1. Entonces los vectores de base dual se dan de la siguiente manera:

e² es el resultado de la rotación e₁ a través de un ángulo de 90° (donde el sentido se mide asumiendo el par e₁, e₂ para ser positivamente orientado), y luego escalar para que e² ⋅ e₂ = 1 sostiene.
e¹ es el resultado de la rotación e₂ a través de un ángulo de 90°, y luego escalar para que e¹ ⋅ e₁ = 1 sostiene.

Aplicando estas reglas, encontramos

mathbf{e}^1 = frac{1}{2}mathbf{e}_1 - frac{1}{sqrt{2}}mathbf{e}_2

{displaystyle mathbf {e} ^{2}=-{frac {1}{sqrt {2}}}mathbf {e} _{1}+2mathbf {e} _{2}.}

Por lo tanto, la matriz de cambio de base al pasar de la base original a la base recíproca es

{displaystyle R={begin{bmatrix}{frac {1}{2}}&-{frac {1}{sqrt {2}}}\-{frac {1}{sqrt {2}}}&2end{bmatrix}},}

desde

{displaystyle [mathbf {e} ^{1} mathbf {e} ^{2}]=[mathbf {e} _{1} mathbf {e} _{2}]{begin{bmatrix}{frac {1}{2}}&-{frac {1}{sqrt {2}}}\-{frac {1}{sqrt {2}}}&2end{bmatrix}}.}

Por ejemplo, el vector

v = frac{3}{2}mathbf{e}_1 + 2mathbf{e}_2

es un vector con componentes contravariantes

v^1 = frac{3}{2},quad v^2 = 2.

Los componentes covariantes se obtienen igualando las dos expresiones para el vector v:

{displaystyle v=v_{1}mathbf {e} ^{1}+v_{2}mathbf {e} ^{2}=v^{1}mathbf {e} _{1}+v^{2}mathbf {e} _{2}}

entonces

{displaystyle {begin{aligned}{begin{bmatrix}v_{1}\v_{2}end{bmatrix}}&=R^{-1}{begin{bmatrix}v^{1}\v^{2}end{bmatrix}}\&={begin{bmatrix}4&{sqrt {2}}\{sqrt {2}}&1end{bmatrix}}{begin{bmatrix}v^{1}\v^{2}end{bmatrix}}\&={begin{bmatrix}6+2{sqrt {2}}\2+{frac {3}{sqrt {2}}}end{bmatrix}}end{aligned}}.}

Espacio euclidiano tridimensional

En el espacio euclidiano tridimensional, también se puede determinar explícitamente la base dual de un conjunto dado de vectores base e₁, e₂, e₃ de E₃ que no necesariamente se supone que son ortogonal ni de norma unitaria. Los vectores de base dual son:

mathbf{e}^1 = frac{mathbf{e}_2 times mathbf{e}_3}{mathbf{e}_1 cdot (mathbf{e}_2 times mathbf{e}_3)}; qquad mathbf{e}^2 = frac{mathbf{e}_3 times mathbf{e}_1}{mathbf{e}_2 cdot (mathbf{e}_3 times mathbf{e}_1)}; qquad mathbf{e}^3 = frac{mathbf{e}_1 times mathbf{e}_2}{mathbf{e}_3 cdot (mathbf{e}_1 times mathbf{e}_2)}.

Incluso cuando e_i y eⁱ no son ortonormales, siguen siendo mutuamente recíprocos:

mathbf{e}^i cdot mathbf{e}_j = delta^i_j,

Entonces, las componentes contravariantes de cualquier vector v se pueden obtener mediante el producto escalar de v con los vectores de base dual:

{displaystyle q^{1}=mathbf {v} cdot mathbf {e} ^{1};qquad q^{2}=mathbf {v} cdot mathbf {e} ^{2};qquad q^{3}=mathbf {v} cdot mathbf {e} ^{3}.}

Del mismo modo, los componentes covariantes de v se pueden obtener del producto escalar de v con vectores base, a saber.

{displaystyle q_{1}=mathbf {v} cdot mathbf {e} _{1};qquad q_{2}=mathbf {v} cdot mathbf {e} _{2};qquad q_{3}=mathbf {v} cdot mathbf {e} _{3}.}

Entonces v se puede expresar de dos formas (recíprocas), a saber.

{displaystyle mathbf {v} =q^{i}mathbf {e} _{i}=q^{1}mathbf {e} _{1}+q^{2}mathbf {e} _{2}+q^{3}mathbf {e} _{3}.}

{displaystyle mathbf {v} =q_{i}mathbf {e} ^{i}=q_{1}mathbf {e} ^{1}+q_{2}mathbf {e} ^{2}+q_{3}mathbf {e} ^{3}}

Combinando las relaciones anteriores, tenemos

{displaystyle mathbf {v} =(mathbf {v} cdot mathbf {e} ^{i})mathbf {e} _{i}=(mathbf {v} cdot mathbf {e} _{i})mathbf {e} ^{i}}

y podemos convertir entre la base y la base dual con

{displaystyle q_{i}=mathbf {v} cdot mathbf {e} _{i}=(q^{j}mathbf {e} _{j})cdot mathbf {e} _{i}=(mathbf {e} _{j}cdot mathbf {e} _{i})q^{j}}

{displaystyle q^{i}=mathbf {v} cdot mathbf {e} ^{i}=(q_{j}mathbf {e} ^{j})cdot mathbf {e} ^{i}=(mathbf {e} ^{j}cdot mathbf {e} ^{i})q_{j}.}

Si los vectores de base son ortonormales, entonces son los mismos que los vectores de base dual.

Espacios euclidianos generales

Más generalmente, en un espacio euclidiano n-dimensional V, si una base es

{displaystyle mathbf {e} _{1},dotsmathbf {e} _{n},}

la base recíproca viene dada por (los índices dobles se suman),

{displaystyle mathbf {e} ^{i}=g^{ij}mathbf {e} _{j}}

donde los coeficientes g^ij son las entradas de la matriz inversa de

g_{{ij}}={mathbf {e}}_{i}cdot {mathbf {e}}_{j}.

De hecho, entonces tenemos

{displaystyle mathbf {e} ^{i}cdot mathbf {e} _{k}=g^{ij}mathbf {e} _{j}cdot mathbf {e} _{k}=g^{ij}g_{jk}=delta _{k}^{i}.}

Los componentes covariante y contravariante de cualquier vector

mathbf{v} = q_i mathbf{e}^i = q^i mathbf{e}_i ,

están relacionados como arriba por

{displaystyle q_{i}=mathbf {v} cdot mathbf {e} _{i}=(q^{j}mathbf {e} _{j})cdot mathbf {e} _{i}=q^{j}g_{ji}}

{displaystyle q^{i}=mathbf {v} cdot mathbf {e} ^{i}=(q_{j}mathbf {e} ^{j})cdot mathbf {e} ^{i}=q_{j}g^{ji}.}

Uso informal

En el campo de la física, el adjetivo covariante a menudo se usa informalmente como sinónimo de invariante. Por ejemplo, la ecuación de Schrödinger no mantiene su forma escrita bajo las transformaciones de coordenadas de la relatividad especial. Por lo tanto, un físico podría decir que la ecuación de Schrödinger no es covariante. Por el contrario, la ecuación de Klein-Gordon y la ecuación de Dirac mantienen su forma escrita bajo estas transformaciones de coordenadas. Por lo tanto, un físico podría decir que estas ecuaciones son covariantes.

A pesar de este uso de "covariante", es más exacto decir que las ecuaciones de Klein-Gordon y Dirac son invariantes y que la ecuación de Schrödinger no es invariante. Adicionalmente, para eliminar la ambigüedad, se debe indicar la transformación mediante la cual se evalúa la invariancia.

Debido a que los componentes de los vectores son contravariantes y los de los covectores son covariantes, a menudo se hace referencia a los propios vectores como contravariantes y a los covectores como covariantes.

Uso en análisis tensorial

La distinción entre covarianza y contravarianza es particularmente importante para los cálculos con tensores, que a menudo tienen varianza mixta. Esto significa que tienen componentes covariantes y contravariantes, o componentes vectoriales y covectoriales. La valencia de un tensor es el número de términos variantes y covariantes y, en la notación de Einstein, los componentes covariantes tienen índices inferiores, mientras que los componentes contravariantes tienen índices superiores. La dualidad entre covarianza y contravarianza interviene cada vez que una cantidad vectorial o tensorial se representa mediante sus componentes, aunque la geometría diferencial moderna utiliza métodos sin índices más sofisticados para representar los tensores.

En el análisis tensorial, un vector covariante varía más o menos recíprocamente con un vector contravariante correspondiente. Las expresiones para longitudes, áreas y volúmenes de objetos en el espacio vectorial se pueden dar en términos de tensores con índices covariantes y contravariantes. Bajo simples expansiones y contracciones de las coordenadas, la reciprocidad es exacta; bajo transformaciones afines los componentes de un vector se entremezclan entre expresión covariante y contravariante.

En una variedad, un campo tensorial normalmente tendrá múltiples índices superior e inferior, donde la notación de Einstein se usa ampliamente. Cuando la variedad está equipada con una métrica, los índices covariante y contravariante se vuelven muy estrechamente relacionados entre sí. Los índices contravariantes se pueden convertir en índices covariantes contrayendo con el tensor métrico. Lo contrario es posible contrayendo con la (matriz) inversa del tensor métrico. Tenga en cuenta que, en general, tal relación no existe en espacios no dotados de un tensor métrico. Además, desde un punto de vista más abstracto, un tensor es simplemente "ahí" y sus componentes de cualquier tipo son solo artefactos de cálculo cuyos valores dependen de las coordenadas elegidas.

La explicación en términos geométricos es que un tensor general tendrá índices contravariantes así como índices covariantes, porque tiene partes que viven tanto en el paquete tangente como en el paquete cotangente.

Un vector contravariante es uno que se transforma como $frac{dx^{mu}}{dtau}$ , donde $x^{mu} !$ son las coordenadas de una partícula en su tiempo apropiado $tau$ . Un vector covariante es uno que se transforma como ${displaystyle {frac {partial varphi }{partial x^{mu }}}}$ , donde $varphi$ es un campo de escalar.

Álgebra y geometría

En la teoría de categorías, existen funtores covariantes y funtores contravariantes. La asignación del espacio dual a un espacio vectorial es un ejemplo estándar de un funtor contravariante. Algunas construcciones de álgebra multilineal son de tipo "mixto" varianza, lo que les impide ser funtores.

En geometría diferencial, las componentes de un vector relativas a una base del fibrado tangente son covariantes si cambian con la misma transformación lineal que un cambio de base. Son contravariantes si cambian por la transformación inversa. Esto es a veces una fuente de confusión por dos razones distintas pero relacionadas. La primera es que los vectores cuyos componentes son covariantes (llamados covectores o formas 1) en realidad retroceden bajo funciones suaves, lo que significa que la operación que asigna el espacio de covectores a una variedad suave es en realidad un funtor contravariante. Del mismo modo, los vectores cuyas componentes son contravariantes avanzan bajo aplicaciones suaves, por lo que la operación que asigna el espacio de vectores (contravariantes) a una variedad suave es un funtor covariante. En segundo lugar, en el enfoque clásico de la geometría diferencial, no son las bases del fibrado tangente el objeto más primitivo, sino los cambios en el sistema de coordenadas. Los vectores con componentes contravariantes se transforman de la misma manera que los cambios en las coordenadas (porque en realidad cambian de manera opuesta al cambio de base inducido). Asimismo, los vectores con componentes covariantes se transforman de manera opuesta a los cambios en las coordenadas.

Contenido relacionado

Más resultados...