Continuidad uniforme

En algún momento el gráfico de f()x)=1x{displaystyle f(x)={tfrac {1}{x}} penetrará la parte superior y/o inferior de una ventana (aquí azul) con altura 0}}" xmlns="http://www.w3.org/1998/Math/MathML">2ε ε ▪ ▪ R■0{displaystyle 2varepsilon in mathbb {R} _{}0}0}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3cdd353040b17bfb0d44451573269765f5f55805" style="vertical-align: -0.671ex; width:9.097ex; height:2.509ex;"/> ancho 0}}" xmlns="http://www.w3.org/1998/Math/MathML">2δ δ ▪ ▪ R■0{displaystyle 2delta in mathbb {R} _{}0}0}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/de77578efacb6e48fb6e6be2c19adb06c94e7944" style="vertical-align: -0.671ex; width:9.063ex; height:2.676ex;"/> mientras ()f){displaystyle (f)} que va más allá de un intervalo inferior a ese ancho, ya que el centro de la ventana se mueve sobre el gráfico en la dirección x=0{displaystyle x=0}. Si existiera una ventana de la parte superior y/o inferior no es penetrada por este gráfico mientras la ventana se mueve sobre el gráfico en la dirección de x=0{displaystyle x=0}, entonces su anchura sería infinitamente pequeña, así f()x){displaystyle f(x)} es no uniformemente continuo. La función g()x)=x{displaystyle g(x)={sqrt {x}}Por otro lado, es uniformemente continuo.

En matemáticas, una función real f{displaystyle f} de números reales se dice que uniformemente continuo si hay un número real positivo δ δ {displaystyle delta } tal que los valores de función sobre cualquier intervalo de dominio de función del tamaño δ δ {displaystyle delta } están tan cerca uno del otro como queremos. En otras palabras, para una función real uniformemente continua de números reales, si queremos que las diferencias de valor de función sean inferiores a cualquier número real positivo ε ε {displaystyle epsilon }, entonces hay un número real positivo δ δ {displaystyle delta } tales que <math alttext="{displaystyle |f(x)-f(y)|Silenciof()x)− − f()Sí.)Silencio.ε ε {displaystyle tenciónf(x)-f(y) intimidad<img alt="{displaystyle |f(x)-f(y)| en cualquier x{displaystyle x} y Sí.{displaystyle y} en cualquier intervalo de función del tamaño δ δ {displaystyle delta }.

La diferencia entre la continuidad uniforme y la continuidad (ordinaria) es que, en continuidad uniforme, existe una aplicación global δ δ {displaystyle delta } (el tamaño de un intervalo de dominio de función sobre el cual las diferencias de valor de función son menos que ε ε {displaystyle epsilon }) que depende sólo de ε ε {displaystyle varepsilon }, mientras que en la continuidad (ordinaria) hay una aplicación local δ δ {displaystyle delta } que depende de los dos ε ε {displaystyle varepsilon } y x{displaystyle x}. Así que la continuidad uniforme es una condición de continuidad más fuerte que la continuidad; una función uniformemente continua es continua pero una función continua no es necesariamente continua. Los conceptos de continuidad y continuidad uniforme pueden ampliarse a funciones definidas entre espacios métricos.

Las funciones continuas pueden dejar de ser uniformemente continuas si no están sujetas a un dominio consolidado, como f()x)=1x{displaystyle f(x)={tfrac {1}{x}} on ()0,1){displaystyle (0,1)}, o si sus pendientes se vuelven sin límites en un dominio infinito, como f()x)=x2{displaystyle f(x)=x^{2} en la línea real (número). Sin embargo, cualquier mapa de Lipschitz entre los espacios métricos es uniformemente continuo, en particular cualquier isometría (mapa previa a la distancia).

Aunque la continuidad se puede definir para funciones entre espacios topológicos generales, definir la continuidad uniforme requiere más estructura. El concepto se basa en comparar los tamaños de las vecindades de distintos puntos, por lo que requiere un espacio métrico o, más generalmente, un espacio uniforme.

Definición de funciones en espacios métricos

Para una función f:X→ → Y{displaystyle f:Xto Sí. con espacios métricos ()X,d1){displaystyle (X,d_{1})} y ()Y,d2){displaystyle (Y,d_{2})}, las siguientes definiciones de continuidad uniforme y continuidad (ordinaria).

Definición de continuidad uniforme

• f{displaystyle f} se llama uniformemente continuo si por cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> existe un número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0} 0 " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> por cada uno x,Sí.▪ ▪ X{displaystyle x,yin X} con <math alttext="{displaystyle d_{1}(x,y)d1()x,Sí.).δ δ {displaystyle d_{1}(x,y)traducidodelta }<img alt="{displaystyle d_{1}(x,y), tenemos <math alttext="{displaystyle d_{2}(f(x),f(y))d2()f()x),f()Sí.)).ε ε {displaystyle d_{2}(f(x),f(y)<img alt="{displaystyle d_{2}(f(x),f(y)). El set <math alttext="{displaystyle {yin X:d_{1}(x,y){}Sí.▪ ▪ X:d1()x,Sí.).δ δ }{displaystyle {yin X:d_{1}(x,y) {}}<img alt="{displaystyle {yin X:d_{1}(x,y) para cada uno x{displaystyle x} es un barrio x{displaystyle x} y el conjunto <math alttext="{displaystyle {xin X:d_{1}(x,y){}x▪ ▪ X:d1()x,Sí.).δ δ }{displaystyle {xin X:d_{1}(x,y) {}}<img alt="{displaystyle {xin X:d_{1}(x,y) para cada uno Sí.{displaystyle y} es un barrio Sí.{displaystyle y} por la definición de un barrio en un espacio métrico.
  • Si X{displaystyle X} y Y{displaystyle Sí. son subconjuntos de la línea real, entonces d1{displaystyle D_{1} y d2{displaystyle D_{2} puede ser el estándar de una dimensión Distancia euroclidiana, dando la siguiente definición: para cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> existe un número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0} 0 " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> por cada uno x,Sí.▪ ▪ X{displaystyle x,yin X}, <math alttext="{displaystyle |x-y|<delta implies |f(x)-f(y)|Silenciox− − Sí.Silencio.δ δ ⟹ ⟹ Silenciof()x)− − f()Sí.)Silencio.ε ε {displaystyle tenciónx-y eternamente identificadodelta implies tenciónf(x)-f(y) sometida recomendadavarepsilon }<img alt="{displaystyle |x-y|<delta implies |f(x)-f(y)| (donde) A⟹ ⟹ B{displaystyle Aimplies B} es una declaración condicional material diciendo "si A{displaystyle A}, entonces B{displaystyle B}").
• Equivalentemente, f{displaystyle f} se dice que es uniformemente continuo si 0;exists delta >0;forall xin X;forall yin X:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y))О О ε ε ■0∃ ∃ δ δ ■0О О x▪ ▪ XО О Sí.▪ ▪ X:d1()x,Sí.).δ δ ⇒ ⇒ d2()f()x),f()Sí.)).ε ε {displaystyle forall varepsilon √0;exists delta ################################################################################################################################################################################################################################################################ X;forall yin X:,d_{1}(x,y) madedelta ,Rightarrow ,d_{2}(f(x),f(y)) madevarepsilon }0;exists delta >0;forall xin X;forall yin X:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y)). Aquí cuantificaciones (0}" xmlns="http://www.w3.org/1998/Math/MathML">О О ε ε ■0{displaystyle forall varepsilon }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ca612654a722b47901243b966d0653e9cc5e9758" style="vertical-align: -0.338ex; width:6.637ex; height:2.176ex;"/>, 0}" xmlns="http://www.w3.org/1998/Math/MathML">∃ ∃ δ δ ■0{displaystyle exists delta }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/256c25caeb7d7b83fb057ce4ee12265dfcbeedae" style="vertical-align: -0.338ex; width:6.602ex; height:2.343ex;"/>, О О x▪ ▪ X{displaystyle forall xin X}, y О О Sí.▪ ▪ X{displaystyle forall yin X}) se utilizan.
• Alternativamente, f{displaystyle f} se dice que es uniformemente continuo si hay una función de todos los números reales positivos ε ε {displaystyle varepsilon }, δ δ ()ε ε ){displaystyle delta (varepsilon)} representando el número real máximo positivo, tal que para cada x,Sí.▪ ▪ X{displaystyle x,yin X} si <math alttext="{displaystyle d_{1}(x,y)d1()x,Sí.).δ δ ()ε ε ){displaystyle d_{1}(x,y)traducidodelta (varepsilon)}<img alt="{displaystyle d_{1}(x,y) entonces <math alttext="{displaystyle d_{2}(f(x),f(y))d2()f()x),f()Sí.)).ε ε {displaystyle d_{2}(f(x),f(y)<img alt="{displaystyle d_{2}(f(x),f(y)). δ δ ()ε ε ){displaystyle delta (varepsilon)} es una función monotonicamente no disminuyente.

Definición de continuidad (ordinaria)

• f{displaystyle f} se llama continuo ax¿Qué? ¿Qué? {displaystyle {compline {text{at }x} si por cada número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> existe un número real 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0} 0 " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> por cada uno Sí.▪ ▪ X{displaystyle yin X} con <math alttext="{displaystyle d_{1}(x,y)d1()x,Sí.).δ δ {displaystyle d_{1}(x,y)traducidodelta }<img alt="{displaystyle d_{1}(x,y), tenemos <math alttext="{displaystyle d_{2}(f(x),f(y))d2()f()x),f()Sí.)).ε ε {displaystyle d_{2}(f(x),f(y)<img alt="{displaystyle d_{2}(f(x),f(y)). El set <math alttext="{displaystyle {yin X:d_{1}(x,y){}Sí.▪ ▪ X:d1()x,Sí.).δ δ }{displaystyle {yin X:d_{1}(x,y) {}}<img alt="{displaystyle {yin X:d_{1}(x,y) es un barrio x{displaystyle x}. Así, la continuidad (ordinaria) es una propiedad local de la función en el punto x{displaystyle x}.
• Equivalentemente, una función f{displaystyle f} se dice que es continuo si 0;exists delta >0;forall yin X:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y))О О x▪ ▪ XО О ε ε ■0∃ ∃ δ δ ■0О О Sí.▪ ▪ X:d1()x,Sí.).δ δ ⇒ ⇒ d2()f()x),f()Sí.)).ε ε {displaystyle forall xin X;forall varepsilon √0;exists delta ################################################################################################################################################################################################################################################################0;exists delta >0;forall yin X:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y)).
• Alternativamente, una función f{displaystyle f} se dice que es continuo si hay una función de todos los números reales positivos ε ε {displaystyle varepsilon } y x▪ ▪ X{displaystyle xin X}, δ δ ()ε ε ,x){displaystyle delta (varepsilonx)} representando el número real máximo positivo, tal que en cada x{displaystyle x} si Sí.▪ ▪ X{displaystyle yin X} satisfizo <math alttext="{displaystyle d_{1}(x,y)d1()x,Sí.).δ δ ()ε ε ,x){displaystyle d_{1}(x,y)traducidodelta (varepsilonx)}<img alt="{displaystyle d_{1}(x,y) entonces <math alttext="{displaystyle d_{2}(f(x),f(y))d2()f()x),f()Sí.)).ε ε {displaystyle d_{2}(f(x),f(y)<img alt="{displaystyle d_{2}(f(x),f(y)). A cada uno x{displaystyle x}, δ δ ()ε ε ,x){displaystyle delta (varepsilonx)} es una función monotonicamente no disminuyente.

Continuidad local versus continuidad global uniforme

En las definiciones, la diferencia entre la continuidad uniforme y la continuidad es que, en la continuidad uniforme, existe una aplicación global δ δ {displaystyle delta } (el tamaño de un barrio en X{displaystyle X} sobre qué valores de la métrica para valores de función Y{displaystyle Sí. son menos que ε ε {displaystyle varepsilon }) que depende sólo de ε ε {displaystyle varepsilon } mientras que en continuidad se aplica localmente δ δ {displaystyle delta } que depende de los dos ε ε {displaystyle varepsilon } y x{displaystyle x}. La continuidad es una local propiedad de una función, es decir, una función f{displaystyle f} es continuo, o no, en un punto particular x{displaystyle x} del dominio de la función X{displaystyle X}, y esto se puede determinar mirando sólo los valores de la función en un barrio arbitrariamente pequeño de ese punto. Cuando hablamos de una función siendo continua en un intervalo, queremos decir que la función es continua en cada punto del intervalo. En cambio, la continuidad uniforme es una mundial propiedad de f{displaystyle f}, en el sentido de que la definición estándar de continuidad uniforme se refiere a cada punto X{displaystyle X}. Por otro lado, es posible dar una definición que es local en términos de la extensión natural fAlternativa Alternativa {displaystyle f^{*}(las características de las cuales en puntos no estándar se determinan por las propiedades globales f{displaystyle f}), aunque no es posible dar una definición local de continuidad uniforme para una función arbitraria de valor hiperreal, véase abajo.

Una definición matemática que una función f{displaystyle f} es continuo en un intervalo I{displaystyle Yo... y una definición que f{displaystyle f} es uniformemente continuo I{displaystyle Yo... son estructuralmente similares como se muestra en lo siguiente.

Continuidad de una función f:X→ → Y{displaystyle f:Xto Sí. para espacios métricos ()X,d1){displaystyle (X,d_{1})} y ()Y,d2){displaystyle (Y,d_{2})} en cada punto x{displaystyle x} de un intervalo I⊆ ⊆ X{displaystyle I 'subseteq X' (es decir, continuidad de f{displaystyle f} en el intervalo I{displaystyle Yo...) se expresa por una fórmula comenzando con cuantificaciones

0;forall xin I;exists delta >0;forall yin I:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y))О О ε ε ■0О О x▪ ▪ I∃ ∃ δ δ ■0О О Sí.▪ ▪ I:d1()x,Sí.).δ δ ⇒ ⇒ d2()f()x),f()Sí.)).ε ε {displaystyle forall varepsilon √0;forall xin I;exists delta ################################################################################################################################################################################################################################################################0;forall xin I;exists delta >0;forall yin I:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y)),

(métricas d1()x,Sí.){displaystyle d_{1}(x,y)} y d2()f()x),f()Sí.)){displaystyle d_{2}(f(x),f(y)} son Silenciox− − Sí.Silencio{displaystyle Silencioso y Silenciof()x)− − f()Sí.)Silencio{displaystyle Silenciof(x)-f(y) para f:R→ → R{displaystyle f:mathbb {R} to mathbb {R} para el conjunto de números reales R{displaystyle mathbb {R}).

Para la continuidad uniforme, el orden de las primeras, segundas y terceras cuantificaciones (О О x▪ ▪ I{displaystyle forall xin I}, 0}" xmlns="http://www.w3.org/1998/Math/MathML">О О ε ε ■0{displaystyle forall varepsilon }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ca612654a722b47901243b966d0653e9cc5e9758" style="vertical-align: -0.338ex; width:6.637ex; height:2.176ex;"/>, y 0}" xmlns="http://www.w3.org/1998/Math/MathML">∃ ∃ δ δ ■0{displaystyle exists delta }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/256c25caeb7d7b83fb057ce4ee12265dfcbeedae" style="vertical-align: -0.338ex; width:6.602ex; height:2.343ex;"/>) se rotan:

0;exists delta >0;forall xin I;forall yin I:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y))О О ε ε ■0∃ ∃ δ δ ■0О О x▪ ▪ IО О Sí.▪ ▪ I:d1()x,Sí.).δ δ ⇒ ⇒ d2()f()x),f()Sí.)).ε ε {displaystyle forall varepsilon √0;exists delta ################################################################################################################################################################################################################################################################ I;forall yin I:,d_{1}(x,y) madedelta ,Rightarrow ,d_{2}(f(x),f(y)) madevarepsilon }0;exists delta >0;forall xin I;forall yin I:,d_{1}(x,y)<delta ,Rightarrow ,d_{2}(f(x),f(y)).

Así, para la continuidad en el intervalo, uno toma un punto arbitrario x{displaystyle x} del intervalo, y entonces debe existir una distancia δ δ {displaystyle delta },

⋯ ⋯ О О x∃ ∃ δ δ ⋯ ⋯ ,{displaystyle cdots forall x,exists delta cdots}

para la continuidad uniforme, un solo δ δ {displaystyle delta } debe trabajar uniformemente para todos los puntos x{displaystyle x} del intervalo,

⋯ ⋯ ∃ ∃ δ δ О О x⋯ ⋯ .{displaystyle cdots exists delta ,forall xcdots. }

Propiedades

Cada función uniformemente continua es continua, pero el contrario no sostiene. Considere por ejemplo la función continua f:: R→ → R,x↦ ↦ x2{displaystyle fcolon mathbb {R} rightarrow mathbb {R}xmapsto x^{2} Donde R{displaystyle mathbb {R} es el conjunto de números reales. Dado un número real positivo ε ε {displaystyle varepsilon }, la continuidad uniforme requiere la existencia de un número real positivo δ δ {displaystyle delta } tal que para todos x1,x2▪ ▪ R{displaystyle x_{1},x_{2}in mathbb {R} con <math alttext="{displaystyle |x_{1}-x_{2}|Silenciox1− − x2Silencio.δ δ {displaystyle Silencio.<img alt="|x_{1}-x_{2}|, tenemos <math alttext="{displaystyle |f(x_{1})-f(x_{2})|Silenciof()x1)− − f()x2)Silencio.ε ε {displaystyle Silenciof(x_{1})-f(x_{2})<img alt="{displaystyle |f(x_{1})-f(x_{2})|. Pero...

f()x+δ δ )− − f()x)=2x⋅ ⋅ δ δ +δ δ 2,{displaystyle fleft(x+delta right)-f(x)=2xcdot delta +delta ^{2}

y como x{displaystyle x} va a ser un valor superior y superior, δ δ {displaystyle delta } necesita ser inferior y inferior para satisfacer <math alttext="{displaystyle |f(x+beta)-f(x)|Silenciof()x+β β )− − f()x)Silencio.ε ε {displaystyle Silenciof(x+beta)-f(x)<img alt="{displaystyle |f(x+beta)-f(x)| para números reales positivos <math alttext="{displaystyle beta β β .δ δ {displaystyle beta<img alt="beta y el dado ε ε {displaystyle varepsilon }. Esto significa que no hay un número real positivo (no importa lo pequeño que sea) δ δ {displaystyle delta } para satisfacer la condición f{displaystyle f} para ser uniformemente continuo f{displaystyle f} no es uniformemente continuo.

Cualquier función absolutamente continua (sobre un intervalo compacto) es uniformemente continua. Por otro lado, la función de Cantor es uniformemente continua pero no absolutamente continua.

La imagen de un subconjunto totalmente acotado bajo una función uniformemente continua está totalmente acotada. Sin embargo, la imagen de un subconjunto acotado de un espacio métrico arbitrario bajo una función uniformemente continua no necesita ser acotada: como contraejemplo, considere la función identidad de los enteros dotados de la métrica discreta a los enteros dotados de la métrica euclidiana usual.

El teorema de Heine-Cantor afirma que toda función continua en un conjunto compacto es uniformemente continua. En particular, si una función es continua en un intervalo acotado cerrado de la línea real, es uniformemente continua en ese intervalo. La integrabilidad de Darboux de funciones continuas se sigue casi inmediatamente de este teorema.

Si una función de valor real f{displaystyle f} continuo [0,JUEGO JUEGO ){displaystyle [0,infty]} y limx→ → JUEGO JUEGO f()x){displaystyle lim _{xto infty }f(x)} existe (y es finito), entonces f{displaystyle f} es uniformemente continuo. En particular, cada elemento C0()R){displaystyle C_{0}(mathbb {R})}, el espacio de funciones continuas en R{displaystyle mathbb {R} que desaparecen al infinito, es uniformemente continuo. Esta es una generalización del teorema Heine-Cantor mencionado anteriormente, ya Cc()R)⊂ ⊂ C0()R){displaystyle C_{c}(mathbb {R})subset C_{0}(mathbb {R})}.

Ejemplos y no ejemplos

Ejemplos

• Funciones lineales x↦ ↦ ax+b{displaystyle xmapsto ax+b} son los ejemplos más simples de funciones uniformemente continuas.
• Cualquier función continua en el intervalo [0,1]{displaystyle [0,1]} es también uniformemente continuo, ya que [0,1]{displaystyle [0,1]} es un conjunto compacto.
• Cada función que es diferente y ha ligado derivado es uniformemente continua.
• Cada mapa continuo de Lipschitz entre dos espacios métricos es uniformemente continuo. Más generalmente, cada función continua Hölder es uniformemente continua.
• La función de valor absoluto es uniformemente continua, a pesar de no ser diferente en x=0{displaystyle x=0}. Esto muestra funciones uniformemente continuas no siempre son diferentes.
• A pesar de ser en ninguna parte diferente, la función Weierstrass es uniformemente continua.
• Cada miembro de un conjunto de funciones uniformemente equicontinua es uniformemente continuo.

No ejemplos

• Las funciones que no están sujetas a un dominio consolidado no son uniformemente continuas. La función tangente es continua en el intervalo ()− − π π /2,π π /2){displaystyle (-pi /2,pi /2)} pero no uniformemente continuo en ese intervalo, ya que va a la infinidad como x→ → π π /2{displaystyle xto pi /2}.
• Las funciones que tienen pendientes que quedan sin límites en un dominio infinito no pueden ser uniformemente continuas. La función exponencial x↦ ↦ ex{displaystyle xmapsto e^{x} es continua en todas partes en la línea real pero no es uniformemente continuo en la línea, ya que su derivado tiende a la infinidad como x→ → JUEGO JUEGO {displaystyle xto infty }.

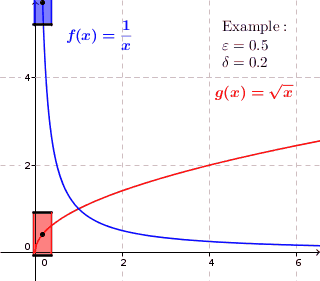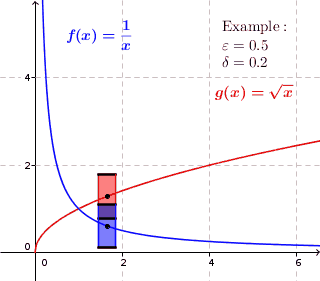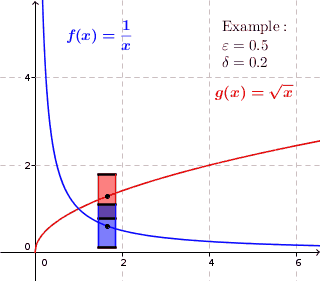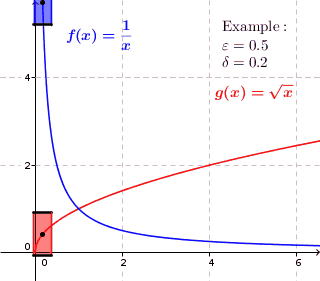
Visualización

Para una función uniformemente continua, para cada número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> hay un número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> tales que dos valores de función f()x){displaystyle f(x)} y f()Sí.){displaystyle f(y)} tienen la distancia máxima ε ε {displaystyle varepsilon } siempre x{displaystyle x} y Sí.{displaystyle y} están dentro de la distancia máxima δ δ {displaystyle delta }. Así en cada punto ()x,f()x)){displaystyle (x,f(x)} del gráfico, si dibujamos un rectángulo con una altura ligeramente inferior a 2ε ε {displaystyle 2varepsilon } y ancho un poco menos que 2δ δ {displaystyle 2delta } alrededor de ese punto, entonces el gráfico se encuentra completamente dentro de la altura del rectángulo, es decir, el gráfico no pasa por la parte superior o inferior del rectángulo. Para funciones que no son uniformemente continuas, esto no es posible; para estas funciones, el gráfico podría estar dentro de la altura del rectángulo en algún punto en el gráfico, pero hay un punto en el gráfico donde el gráfico está arriba o debajo del rectángulo. (el gráfico penetra el lado superior o inferior del rectángulo.)

• 

  Para funciones uniformemente continuas, para cada número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> hay un número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> tal que cuando dibujamos un rectángulo alrededor de cada punto del gráfico con un ancho ligeramente inferior a 2δ δ {displaystyle 2delta } y una altura ligeramente inferior a 2ε ε {displaystyle 2varepsilon }, el gráfico se encuentra completamente dentro de la altura del rectángulo.

• 

  Para funciones que no son uniformemente continuas, hay un número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> tal que por cada número real positivo 0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ■0{displaystyle delta >0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/595d5cea06fdcaf2642caf549eda2cfc537958a9" style="vertical-align: -0.338ex; width:5.31ex; height:2.343ex;"/> hay un punto en el gráfico para que cuando dibujamos un rectángulo con una altura ligeramente inferior a 2ε ε {displaystyle 2varepsilon } y un ancho ligeramente inferior a 2δ δ {displaystyle 2delta } alrededor de ese punto, hay un valor de función directamente encima o debajo del rectángulo. Puede haber un punto gráfico donde el gráfico está completamente dentro de la altura del rectángulo, pero esto no es cierto para cada punto del gráfico.

Historia

La primera definición publicada de continuidad uniforme fue de Heine en 1870, y en 1872 publicó una prueba de que una función continua en un intervalo abierto no necesita ser uniformemente continua. Las pruebas son casi textuales dadas por Dirichlet en sus conferencias sobre integrales definidas en 1854. La definición de continuidad uniforme aparece antes en el trabajo de Bolzano donde también demostró que las funciones continuas en un intervalo abierto no necesitan ser uniformemente continuas. Además, también afirma que una función continua en un intervalo cerrado es uniformemente continua, pero no da una prueba completa.

Otras caracterizaciones

Análisis no estándar

En análisis no estándar, una función de valor real f{displaystyle f} de una variable real es microcontinua en un punto a{displaystyle a} precisamente si la diferencia fAlternativa Alternativa ()a+δ δ )− − fAlternativa Alternativa ()a){displaystyle f^{*}(a+delta)-f^{*}(a)} es infinitesimal cada vez δ δ {displaystyle delta } es infinitesimal. Así f{displaystyle f} es continuo en un conjunto A{displaystyle A} dentro R{displaystyle mathbb {R} precisamente si fAlternativa Alternativa {displaystyle f^{*} es microcontinua en cada punto real a▪ ▪ A{displaystyle ain A}. La continuidad uniforme se puede expresar como la condición de que (la extensión natural de) f{displaystyle f} es microcontinua no sólo en puntos reales en A{displaystyle A}, pero en todos los puntos en su contraparte no estándar (extensión natural) Alternativa Alternativa A{displaystyle ^{*}A} dentro Alternativa Alternativa R{displaystyle ^{*}Mathbb {R}. Tenga en cuenta que existen funciones de valor hiperreal que cumplen este criterio pero no son uniformemente continuas, así como funciones de valor hiperreal uniformemente continuas que no cumplen este criterio, sin embargo, tales funciones no pueden expresarse en la forma fAlternativa Alternativa {displaystyle f^{*} para cualquier función de valor real f{displaystyle f}. (ver cálculo no estándar para más detalles y ejemplos).

Continuidad de Cauchy

Para una función entre los espacios métricos, la continuidad uniforme implica continuidad Cauchy (Fitzpatrick 2006). Más específicamente, vamos A{displaystyle A} ser un subconjunto de Rn{displaystyle mathbb {R} {} {}} {fn}}. Si una función f:A→ → Rn{displaystyle f:Ato mathbb {R} {fn} es uniformemente continuo entonces para cada par de secuencias xn{displaystyle x_{n} y Sí.n{displaystyle y_{n} tales que

limn→ → JUEGO JUEGO Silencioxn− − Sí.nSilencio=0{displaystyle lim _{nto infty - ¿Qué?

tenemos

limn→ → JUEGO JUEGO Silenciof()xn)− − f()Sí.n)Silencio=0.{displaystyle lim _{ntoinfty } torturaf(x_{n})-f(y_{n})

Relaciones con el problema de la extensión

Vamos X{displaystyle X} ser un espacio métrico, S{displaystyle S. a subset of X{displaystyle X}, R{displaystyle R. un espacio métrico completo, y f:S→ → R{displaystyle f:Srightarrow R. una función continua. Una pregunta para responder: Cuándo puede f{displaystyle f} se extendió a una función continua en todos los X{displaystyle X}?

Si S{displaystyle S. está cerrado X{displaystyle X}, la respuesta es dada por el teorema de extensión Tietze. Así que es necesario y suficiente para extender f{displaystyle f} al cierre del S{displaystyle S. dentro X{displaystyle X}: es decir, podemos asumir sin pérdida de generalidad que S{displaystyle S. es denso en X{displaystyle X}, y esto tiene la consecuencia más agradable que si la extensión existe, es único. Una condición suficiente f{displaystyle f} para extenderse a una función continua f:X→ → R{displaystyle f:Xrightarrow R. es que es Cauchy-continuous, es decir, la imagen bajo f{displaystyle f} de una secuencia Cauchy sigue siendo Cauchy. Si X{displaystyle X} es completo (y por lo tanto la terminación de S{displaystyle S.), entonces cada función continua de X{displaystyle X} a un espacio métrico Y{displaystyle Sí. Es Cauchy-continuous. Por lo tanto, cuando X{displaystyle X} está completo, f{displaystyle f} se extiende a una función continua f:X→ → R{displaystyle f:Xrightarrow R. si f{displaystyle f} Es Cauchy-continuous.

Es fácil ver que cada función uniformemente continua es Cauchy-continuous y así se extiende a X{displaystyle X}. El contrario no sostiene, ya que la función f:R→ → R,x↦ ↦ x2{displaystyle f:Rrightarrow R,xmapsto x^{2} es, como se ve arriba, no uniformemente continuo, pero es continuo y por lo tanto Cauchy continuo. En general, para funciones definidas en espacios sin límites como R{displaystyle R., la continuidad uniforme es una condición bastante fuerte. Es deseable tener una condición más débil de la que deducir la extensibilidad.

Por ejemplo, supongamos 1}" xmlns="http://www.w3.org/1998/Math/MathML">a■1{displaystyle a confía1} 1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bc5b9d9fb0ff9d4455e75ccd29676bd7f33da80e" style="vertical-align: -0.338ex; width:5.491ex; height:2.176ex;"/> es un número real. En el nivel precalculus, la función f:x↦ ↦ ax{displaystyle f:xmapsto a^{x} se puede dar una definición precisa sólo para los valores racionales x{displaystyle x} (asumiendo la existencia de qth raíces de números reales positivos, una aplicación del Teorema de Valor Intermedio). A uno le gustaría ampliar f{displaystyle f} a una función definida en todos los R{displaystyle R.. La identidad

f()x+δ δ )− − f()x)=ax()aδ δ − − 1){displaystyle f(x+delta)-f(x)=a^{x}left(a^{delta }-1right)}

muestra que f{displaystyle f} no es uniformemente continuo en el conjunto Q{displaystyle Q} de todos los números racionales; sin embargo para cualquier intervalo I{displaystyle Yo... la restricción de f{displaystyle f} a Q∩ ∩ I{displaystyle Qcap I} es uniformemente continuo, por lo tanto Cauchy-continuous, por lo tanto f{displaystyle f} se extiende a una función continua en I{displaystyle Yo.... Pero como esto es para todos I{displaystyle Yo..., entonces hay una extensión única f{displaystyle f} a una función continua en todos R{displaystyle R..

Más generalmente, una función continua f:S→ → R{displaystyle f:Srightarrow R. cuya restricción a cada subconjunto S{displaystyle S. es uniformemente continuo es extensible X{displaystyle X}, y el contrario sostiene si X{displaystyle X} es localmente compacto.

Una aplicación típica de la extensibilidad de una función uniformemente continua es la prueba de la fórmula de la transformación inversa de Fourier. Primero demostramos que la fórmula es verdadera para las funciones de prueba, hay muchas de ellas. Luego extendemos el mapa inverso a todo el espacio usando el hecho de que el mapa lineal es continuo; por lo tanto, uniformemente continua.

Generalización a espacios vectoriales topológicos

En el caso especial de dos espacios vectoriales topológicos V{displaystyle V} y W{displaystyle W., la noción de continuidad uniforme de un mapa f:V→ → W{displaystyle f:Vto W} se convierte en: para cualquier barrio B{displaystyle B} de cero en W{displaystyle W., existe un vecindario A{displaystyle A} de cero en V{displaystyle V} tales que v1− − v2▪ ▪ A{displaystyle v_{1}-v_{2}in A} implicación f()v1)− − f()v2)▪ ▪ B.{displaystyle f(v_{1})-f(v_{2}in B.}

Para transformaciones lineales f:V→ → W{displaystyle f:Vto W}, la continuidad uniforme es equivalente a la continuidad. Este hecho se utiliza con frecuencia implícitamente en el análisis funcional para extender un mapa lineal fuera de un subespacio denso de un espacio de Banach.

Generalización a espacios uniformes

Así como el escenario más natural y general para la continuidad son los espacios topológicos, el escenario más natural y general para el estudio de uniforme continuidad son los espacios uniformes. Una función f:X→ → Y{displaystyle f:Xto Sí. entre espacios uniformes se llama uniformemente continuo si por cada séquito V{displaystyle V} dentro Y{displaystyle Sí. existe un séquito U{displaystyle U} dentro X{displaystyle X} por cada uno ()x1,x2){displaystyle (x_{1},x_{2}} dentro U{displaystyle U} tenemos ()f()x1),f()x2)){displaystyle (f(x_{1}),f(x_{2})} dentro V{displaystyle V}.

En este contexto, también es cierto que los mapas uniformemente continuos transforman las secuencias de Cauchy en secuencias de Cauchy.

Cada espacio compacto de Hausdorff posee exactamente una estructura uniforme compatible con la topología. Una consecuencia es una generalización del teorema de Heine-Cantor: cada función continua desde un espacio compacto de Hausdorff hasta un espacio uniforme es uniformemente continua.