Teorema de corte mínimo de flujo máximo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Análisis de cortes en una red de flujo — Cortes mínimos de flujo máximo en una red, destacando caminos de máximo flujo para 19 unidades

El teorema de corte mínimo de flujo máximo es un teorema de optimización de flujo, este establece que la cantidad máxima de flujo que puede pasar de un origen a un final, en una red, es exactamente igual al peso total de las aristas en un corte mínimo. Es decir, el peso mínimo de las aristas que al ser eliminadas, provocarían la desconexión entre la fuente y el sumidero.

El teorema se ha denominado de diferentes formas, como teorema de flujo mínimo, teorema de flujo máximo, teorema de corte y teorema de flujo, debido a que crea una relación directa entre dos componentes clave en una red de flujo: el flujo máximo que puede tener y el corte mínimo que representa el paso del flujo máximo. Puede entenderse como un teorema sobre el mínimo corte de máximo flujo.

El teorema es un caso especial del teorema de dualidad para programas lineales, y permite derivar otros teoremas fundamentales como el teorema de Menger y el teorema de König-Egerváry. Estos teoremas tienen aplicaciones significativas en diversos campos, desde la informática hasta la investigación operativa, la ingeniería de redes y la teoría de optimización.

Su importancia radica en su capacidad para resolver problemas complejos de redes, donde es crucial determinar la eficiencia máxima en el flujo de datos o recursos. En la informática, este teorema se aplica para optimizar el rendimiento de redes, asegurando una distribución y un flujo de datos eficientes y efectivos. En la teoría de optimización, proporciona una base sólida para desarrollar algoritmos que buscan maximizar o minimizar ciertas variables dentro de un sistema dado. La relevancia de este teorema se extiende a múltiples aplicaciones prácticas, desde la planificación de rutas de transporte hasta la gestión de redes de telecomunicaciones y la optimización de procesos en sistemas complejos.

HSD

Definiciones y declaración

El teorema iguala dos cantidades: el caudal máximo a través de una red y la capacidad mínima de un corte de la red. Para enunciar el teorema, primero se debe definir cada una de estas nociones.

Red

Una red consta de

un gráfico dirigido finito $N = V, E)$ , donde V denota el conjunto finito de vértices y $E \subseteq V \times V$ es el conjunto de bordes dirigidos;
a fuente $s ▪ V$ y a fregadero $t ▪ V$ ;
a capacidad función, que es un mapeo ${displaystyle c:Eto mathbb {R} ^{+}}$ denotado por $c uv$ o $c () u, v)$ para $() u, v) E$ . Representa la cantidad máxima de flujo que puede pasar a través de un borde.

Flujos

A flujo a través de una red es un mapeo ${displaystyle f:Eto mathbb {R} ^{+}}$ denotado por ${displaystyle f_{uv}}$ o ${displaystyle f(u,v)}$ , con sujeción a las dos limitaciones siguientes:

Capacity Constraint: Por cada borde $(u,v)in E$ , ${displaystyle f_{uv}leq c_{uv}.}$
Conservación de los flujosPara cada vértice $v$ aparte de $s$ y $t$ i.e. the source and sink, respectively), the following equality holds:
${displaystyle sum nolimits _{{u:(u,v)in E}}f_{uv}=sum nolimits _{{w:(v,w)in E}}f_{vw}.}$

Un flujo se puede visualizar como un flujo físico de un fluido a través de la red, siguiendo la dirección de cada borde. Entonces, la restricción de capacidad dice que el volumen que fluye a través de cada borde por unidad de tiempo es menor o igual que la capacidad máxima del borde, y la restricción de conservación dice que la cantidad que fluye hacia cada vértice es igual a la cantidad que fluye hacia afuera de cada vértice, aparte de los vértices fuente y sumidero.

El valor de un flujo está definido por

{displaystyle |f|=sum nolimits _{{v:(s,v)in E}}f_{sv}=sum nolimits _{{v:(v,t)in E}}f_{vt},}

, donde se encuentra $s$ es la fuente y $t$ es el fregadero de la red. En la analogía del fluido, representa la cantidad de líquido que entra en la red en la fuente. Debido al axioma de conservación para los flujos, esta es la misma cantidad de flujo que deja la red en el fregadero.

El problema de flujo máximo pide el flujo más grande en una red determinada.

Problema de flujo máximo. Maximizar $|f|$ , es decir, para recorrer el mayor flujo posible $s$ a $t$ .

Cortes

La otra mitad del teorema de corte max-flow se refiere a un aspecto diferente de una red: la colección de cortes. An S-t cortado $C = S, T)$ es una partición de $V$ tales que $s ▪ S$ y $t ▪ T$ . Eso es, un s-t cortado es una división de los vértices de la red en dos partes, con la fuente en una parte y el lavabo en la otra. El corte-set $X_{C}$ de un corte $C$ es el conjunto de bordes que conectan la parte fuente del corte a la parte del fregadero:

{displaystyle X_{C}:={(u,v)in E: uin S,vin T}=(Stimes T)cap E.}

Por lo tanto, si se eliminan todos los bordes en el conjunto de corte de $C$ , entonces no es posible un flujo positivo, porque no hay una ruta en el gráfico resultante desde la fuente hasta el sumidero.

La capacidad de un corte s-t es la suma de las capacidades de los bordes en su conjunto de corte,

{displaystyle c(S,T)=sum nolimits _{(u,v)in X_{C}}c_{uv}=sum nolimits _{(i,j)in E}c_{ij}d_{ij},}

Donde $d_{ij}=1$ si $iin S$ y $jin T$ , ${displaystyle 0}$ De lo contrario.

Por lo general, hay muchos cortes en un gráfico, pero los cortes con pesos más pequeños suelen ser más difíciles de encontrar.

Problema de corte mínimo. Minimize

c () S, T)

, es decir, determinar

S

T

tal que la capacidad del corte s-t es mínima.

Teorema principal

En la situación anterior, se puede probar que el valor de cualquier flujo a través de una red es menor o igual a la capacidad de cualquier corte s-t, y que además un flujo con valor máximo y un corte con capacidad mínima existen. El teorema principal vincula el valor máximo de caudal con la mínima capacidad de corte de la red.

Teorema de corte minado de flujo máximo. El valor máximo de un flujo s-t es igual a la capacidad mínima sobre todos los cortes s-t.

Ejemplo

Un flujo máximo en una red. Cada borde está etiquetado con f/c, donde f es el flujo sobre el borde y c es la capacidad del borde. El valor de flujo es 5. Hay varios mínimos s-t cortes con capacidad 5; uno es S=s,p} y T=o, q, r, t}.

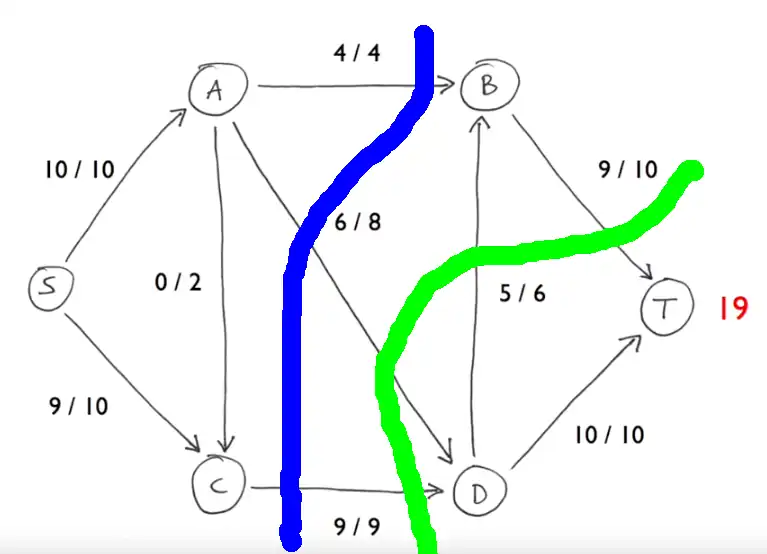
La figura de la derecha muestra un flujo en una red. La anotación numérica en cada flecha, en la forma f/c, indica el caudal (f) y la capacidad (c) de la flecha. Los flujos que emanan de la fuente suman cinco (2+3=5), al igual que los flujos hacia el sumidero (2+3=5), estableciéndose que el valor del flujo es 5.

Un corte s-t con valor 5 viene dado por S={s, p} y T={o, q, r, t}. Las capacidades de los filos que cruzan este corte son 3 y 2, dando una capacidad de corte de 3+2=5. (La flecha de o a p no se considera, ya que apunta de T a S).

El valor del caudal es igual a la capacidad del corte, mostrando que el caudal es un caudal máximo y el corte es un corte mínimo.

Tenga en cuenta que el flujo a través de cada una de las dos flechas que conectan S a T está a plena capacidad; este es siempre el caso: un corte mínimo representa un 'cuello de botella' del sistema.

Formulación de programa lineal

El problema de flujo máximo y el problema de corte mínimo se pueden formular como dos programas lineales primal-dual.

	Max-flow (Primal)	Min-cut (Dual)
variables	${displaystyle f_{uv}}$ ${displaystyle forall (u,v)in E}$ [una variable por borde]	${displaystyle d_{uv}}$ ${displaystyle forall (u,v)in E}$ [una variable por borde] ${displaystyle z_{v}}$ ${displaystyle forall vin Vsetminus {s,t}}$ [una variable por nodo no terminal]
objetivo	maximizar ${displaystyle sum nolimits _{v:(s,v)in E}f_{sv}}$ [Afluencia total máxima de la fuente]	minimizar ${displaystyle sum nolimits _{(u,v)in E}c_{uv}d_{uv}}$ [capacidad total de los bordes cortados]
limitaciones	sujeto a ${displaystyle {begin{aligned}f_{uv}&leq c_{uv}&&forall (u,v)in E\sum _{u}f_{uv}-sum _{w}f_{vw}&=0&&vin Vsetminus {s,t}end{aligned}}}$ [una limitación por borde y una limitación por nodo no terminal]	sujeto a ${displaystyle {begin{aligned}d_{uv}-z_{u}+z_{v}&geq 0&&forall (u,v)in E,uneq s,vneq t\d_{sv}+z_{v}&geq 1&&forall (s,v)in E,vneq t\d_{ut}-z_{u}&geq 0&&forall (u,t)in E,uneq s\d_{st}&geq 1&&{text{if }}(s,t)in Eend{aligned}}}$ [una limitación por borde]
restricciones de firma	${displaystyle {begin{aligned}f_{uv}&geq 0&&forall (u,v)in E\end{aligned}}}$	${displaystyle {begin{aligned}d_{uv}&geq 0&&forall (u,v)in E\z_{v}&in mathbb {R} &&forall vin Vsetminus {s,t}end{aligned}}}$

El LP de flujo máximo es sencillo. El PL dual se obtiene usando el algoritmo descrito en el programa lineal dual: las variables y las restricciones de signo del dual corresponden a las restricciones del primario, y las restricciones del dual corresponden a las variables y las restricciones de signo del primario. El LP resultante requiere alguna explicación. La interpretación de las variables en el LP min-cut es:

{displaystyle d_{uv}={begin{cases}1,&{text{if }}uin S{text{ and }}vin T{text{ (the edge }}uv{text{ is in the cut) }}\0,&{text{otherwise}}end{cases}}}

{displaystyle z_{v}={begin{cases}1,&{text{if }}vin S\0,&{text{otherwise}}end{cases}}}

El objetivo de minimización suma la capacidad sobre todos los bordes que están contenidos en el corte.

Las restricciones garantizan que las variables de hecho representan un corte legal:

Las limitaciones ${displaystyle d_{uv}-z_{u}+z_{v}geq 0}$ (equivalente a ${displaystyle d_{uv}geq z_{u}-z_{v}}$ ) garantizar que, para los nodos no terminales u,v, si u está dentro S y v está dentro T, entonces el borde (u,v) se cuenta en el corte ( ${displaystyle d_{uv}geq 1}$ ).
Las limitaciones ${displaystyle d_{sv}+z_{v}geq 1}$ (equivalente a ${displaystyle d_{sv}geq 1-z_{v}}$ ) garantizar que, si v está dentro T, entonces el borde (s,v) se cuenta en el corte (ya s es por definición en S).
Las limitaciones ${displaystyle d_{ut}-z_{u}geq 0}$ (equivalente a ${displaystyle d_{ut}geq z_{u}}$ ) garantizar que, si u está dentro S, entonces el borde (u,t) se cuenta en el corte (ya t es por definición en T).

Tenga en cuenta que, dado que se trata de un problema de minimización, no tenemos que garantizar que un borde no esté en el corte; solo tenemos que garantizar que cada borde que debería estar en el corte, se suma en la función objetivo.

La igualdad en el teorema de flujo máximo y corte mínimo se deriva del teorema de dualidad fuerte en programación lineal, que establece que si el programa primal tiene una solución óptima, x*, entonces el programa dual también tiene una solución óptima, y*, tal que los valores óptimos formados por las dos soluciones son iguales.

Aplicaciones

Teorema de flujo máximo de Cederbaum

El problema de flujo máximo se puede formular como la maximización de la corriente eléctrica a través de una red compuesta de elementos resistivos no lineales. En esta formulación, el límite de la corriente $I dentro$ entre los terminales de entrada de la red eléctrica como el voltaje de entrada $V dentro$ enfoques $infty$ , es igual al peso del conjunto de corte de peso mínimo.

{displaystyle lim _{V_{text{in}}to infty }(I_{in})=min _{X_{C}}sum _{(u,v)in X_{C}}c_{uv}}

Teorema de corte mínimo de flujo máximo generalizado

Además de la capacidad de borde, considere que hay capacidad en cada vértice, es decir, un mapeo ${displaystyle c:Vto mathbb {R} ^{+}}$ denotado por $c () v)$ , tal que el flujo $f$ tiene que satisfacer no sólo la limitación de la capacidad y la conservación de los flujos, sino también la limitación de la capacidad del vértice

{displaystyle forall vin Vsetminus {s,t}:qquad sum nolimits _{{uin Vmid (u,v)in E}}f_{uv}leq c(v).}

En otras palabras, la cantidad de flujo que pasa por un vértice no puede exceder su capacidad. Defina un s-t corte para que sea el conjunto de vértices y aristas tal que para cualquier ruta desde s a t, la ruta contiene un miembro del Corte. En este caso, la capacidad del corte es la suma de la capacidad de cada arista y vértice del mismo.

En esta nueva definición, el teorema de corte mínimo de flujo máximo generalizado establece que el valor máximo de un flujo s-t es igual a la capacidad mínima de un corte s-t en el nuevo sentido.

Teorema de Menger

En el problema de caminos disjuntos de aristas no dirigidos, tenemos un gráfico no dirigido $G = (V, E)$ y dos vértices $s$ y $t$ , y tenemos que encontrar el número máximo de rutas s-t disjuntas de borde en $G$ .

El teorema de Menger establece que el número máximo de rutas s-t disjuntas de aristas en un gráfico no dirigido es igual al número mínimo de aristas en un conjunto de cortes s-t.

Problema de selección de proyectos

Formulación de red del problema de selección de proyectos con la solución óptima

En el problema de selección de proyectos, hay $n$ proyectos y $m$ máquinas. Cada proyecto $p i$ produce ingresos $r (p i)$ y cada máquina $q j$ cuesta $c (q j)$ para comprar. Cada proyecto requiere un número de máquinas y cada máquina puede ser compartida por varios proyectos. El problema es determinar qué proyectos y máquinas deben seleccionarse y comprarse respectivamente, de modo que se maximice la ganancia.

Sea $P$ el conjunto de proyectos no seleccionados y $Q$ sea el conjunto de máquinas compradas, entonces el problema se puede formular como,

max{g}=sum _{i}r(p_{i})-sum _{p_{i}in P}r(p_{i})-sum _{q_{j}in Q}c(q_{j}).

Dado que el primer término no depende de la elección de $P$ y $P$ , este problema de maximización se puede formular como un problema de minimización, es decir,

min{g'}=sum _{p_{i}in P}r(p_{i})+sum _{q_{j}in Q}c(q_{j}).

El problema de minimización anterior se puede formular como un problema de corte mínimo mediante la construcción de una red, donde la fuente está conectada a los proyectos con capacidad $r (p i)$ , y el fregadero está conectado por las máquinas con capacidad $c (q j)$ . Una arista $(p i, q j)$ con Se agrega capacidad infinita si el proyecto $p i$ requiere máquina q_j. El conjunto de corte s-t representa los proyectos y máquinas en $P$ y $Q$ respectivamente. Por el teorema de corte mínimo de flujo máximo, uno puede resolver el problema como un problema de flujo máximo.

La figura de la derecha ofrece una formulación de red del siguiente problema de selección de proyectos:

	Proyecto $r () p i)$	Máquina $c () q j)$
1	100	200	El proyecto 1 requiere máquinas 1 y 2.
2	200	100	El proyecto 2 requiere máquina 2.
3	150	50	Proyecto 3 requiere máquina 3.

La capacidad mínima de un corte s-t es 250 y la suma de los ingresos de cada proyecto es 450; por lo tanto, la ganancia máxima g es 450 − 250 = 200, seleccionando proyectos $p 2$ y $p 3$ .

La idea aquí es 'fluir' las ganancias de cada proyecto a través de las 'tuberías' de sus máquinas. Si no podemos llenar la tubería desde una máquina, el rendimiento de la máquina es menor que su costo, y el algoritmo de corte mínimo encontrará más barato reducir el margen de beneficio del proyecto en lugar de la máquina. margen de costo.

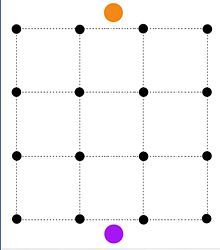
Problema de segmentación de imágenes

Cada nodo negro denota un pixel.

En el problema de segmentación de imágenes, hay $n$ píxeles. A cada píxel $i$ se le puede asignar un valor de primer plano $f i$ o un valor de fondo $b i$ . Hay una penalización de $p ij$ si los píxeles $i, j$ son adyacentes y tienen diferentes asignaciones. El problema es asignar píxeles al primer plano o al fondo de modo que la suma de sus valores menos las penalizaciones sea máxima.

Sea $P$ el conjunto de píxeles asignados al primer plano y $Q$ sea el conjunto de puntos asignados al fondo, entonces el problema se puede formular como,

{displaystyle max{g}=sum _{iin P}f_{i}+sum _{iin Q}b_{i}-sum _{iin P,jin Qlor jin P,iin Q}p_{ij}.}

Este problema de maximización se puede formular como un problema de minimización, es decir,

{displaystyle min{g'}=sum _{iin P,jin Qlor jin P,iin Q}p_{ij}.}

El problema de minimización anterior se puede formular como un problema de corte mínimo construyendo una red donde la fuente (nodo naranja) está conectada a todos los píxeles con capacidad $f i$ , y el sumidero (nodo morado) está conectado por todos los píxeles con capacidad $b i$ . Dos bordes ( $i, j$ ) y ( $j, i$ ) con capacidad $p ij$ se agregan entre dos píxeles adyacentes. El conjunto de cortes s-t representa los píxeles asignados al primer plano en $P$ y los píxeles asignados al fondo en $Q$ .

Historia

Ford y Fulkerson dieron un relato del descubrimiento del teorema en 1962:

"En la primavera de 1955, T.E. Harris, quien, junto con el general F. S. Ross (retirado), había formulado un modelo simplificado de flujo de tráfico ferroviario y señaló este problema particular como el central sugerido por el modelo. No pasó mucho tiempo después de esto hasta que se conjeturó y estableció el resultado principal, el teorema 5.1, al que llamamos teorema de flujo máximo y corte mínimo. Desde entonces han aparecido varias pruebas."

Prueba

Sea $G = (V, E)$ una red (grafo dirigido) con $s$ y $t$ siendo la fuente y el sumidero de $G$ respectivamente.

Considere el flujo $f$ calculado para $G$ por el algoritmo de Ford-Fulkerson. En el gráfico residual $(G f)$ obtenido para $G$ (después de la asignación de flujo final por el algoritmo de Ford-Fulkerson), defina dos subconjuntos de vértices de la siguiente manera:

$A$ : el conjunto de vértices alcanzable desde $s$ dentro $G f$
$A c$ : el conjunto de vértices restantes es decir. $V - A$

Reclamo. $valor(f) = c (A, A c)$ , donde la capacidad de un corte s-t está definida por

c(S,T)=sum nolimits _{(u,v)in Stimes T}c_{uv}

Ahora, lo sabemos, ${displaystyle value(f)=f_{out}(A)-f_{in}(A)}$ para cualquier subconjunto de vértices, $A$ . Por lo tanto, $valor(f) c () A, A c)$ Necesitamos:

Todos bordes salientes del corte debe ser totalmente saturada.
Todos bordes entrantes al corte debe haber Flujo cero.

Para probar la afirmación anterior, consideramos dos casos:

In $G$ , existe un borde saliente $(x,y),xin A,yin A^{c}$ tal que no sea saturado, es decir, $f () x, Sí.) c xy$ . Esto implica, que existe borde delantero desde $x$ a $Sí.$ dentro $G f$ , por lo tanto existe un camino desde $s$ a $Sí.$ dentro $G f$ , que es una contradicción. Por lo tanto, cualquier borde saliente $() x, Sí.)$ está completamente saturada.
In $G$ , existe un borde entrante $(y,x),xin A,yin A^{c}$ tal que lleva algún flujo no cero, es decir, $f () Sí., x) 0$ . Esto implica, que existe Al revés desde $x$ a $Sí.$ dentro $G f$ , por lo tanto existe un camino desde $s$ a $Sí.$ dentro $G f$ , que es otra vez una contradicción. Por lo tanto, cualquier borde entrante $() Sí., x)$ debe tener cero flujo.

Las dos afirmaciones anteriores prueban que la capacidad de corte obtenida de la manera descrita anteriormente es igual al caudal obtenido en la red. Además, el flujo se obtuvo mediante el algoritmo de Ford-Fulkerson, por lo que también es el flujo máximo de la red.

Además, dado que cualquier flujo en la red es siempre menor o igual a la capacidad de cada corte posible en una red, el corte descrito anteriormente es también el corte mínimo que obtiene el flujo máximo.

Un corolario de esta prueba es que el flujo máximo a través de cualquier conjunto de aristas en un corte de un gráfico es igual a la capacidad mínima de todos los cortes anteriores.

Contenido relacionado

Más resultados...