Conjunto convexo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En geometría, conjunto cuya intersección con cada línea es un segmento de línea única

Ilustración de un conjunto convexo que parece un círculo deformado. El segmento de línea, ilustrado en negro arriba, uniendo puntos x y, está completamente dentro del conjunto, ilustrado en verde. Puesto que esto es cierto para cualquier ubicación potencial de cualquier dos puntos dentro del conjunto anterior, el conjunto es convex.

Ilustración de un conjunto no-convexo. Ilustrado por el segmento de línea anterior por el que cambia del color negro al color rojo. Exentrar por qué este conjunto anterior, ilustrado en verde, no es convexo.

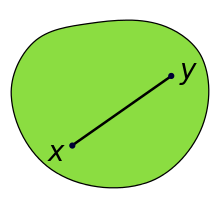
En geometría, un subconjunto de un espacio euclidiano, o más generalmente un espacio afín sobre los reales, es convexo si, dados dos puntos cualesquiera en el subconjunto, el subconjunto contiene el segmento de línea completo que se une a ellos. De manera equivalente, un conjunto convexo o una región convexa es un subconjunto que cruza cada línea en un solo segmento de línea (posiblemente vacío). Por ejemplo, un cubo sólido es un conjunto convexo, pero cualquier cosa que sea hueca o tenga una muesca, por ejemplo, una forma de media luna, no es convexa.

El límite de un conjunto convexo es siempre una curva convexa. La intersección de todos los conjuntos convexos que contienen un subconjunto dado $A$ del espacio euclidiano se denomina envolvente convexa de $A$ . Es el conjunto convexo más pequeño que contiene $A$ .

Una función convexa es una función de valor real definida en un intervalo con la propiedad de que su epígrafe (el conjunto de puntos sobre o sobre el gráfico de la función) es un conjunto convexo. La minimización convexa es un subcampo de optimización que estudia el problema de minimizar funciones convexas sobre conjuntos convexos. La rama de las matemáticas dedicada al estudio de las propiedades de los conjuntos convexos y de las funciones convexas se denomina análisis convexo.

La noción de un conjunto convexo se puede generalizar como se describe a continuación.

Definiciones

Una función es convexa si y sólo si su epígrafe, la región (en verde) sobre su gráfico (en azul), es un conjunto convexo.

Sea $S$ un espacio vectorial o un espacio afín sobre los números reales o, más generalmente, sobre algún campo ordenado. Esto incluye espacios euclidianos, que son espacios afines. Un subconjunto $C$ de $S$ es convexo si, para todo $x$ y $y$ en $C$ , el segmento de línea que conecta $x$ y $y$ se incluyen en $C$ . Esto significa que la combinación afín $(1 - t) x + ty$ pertenece a $C$ , para todas las $x$ y $y$ en $C$ y $t$ en el intervalo $[0, 1]$ . Esto implica que la convexidad (la propiedad de ser convexo) es invariante bajo transformaciones afines. Esto implica también que un conjunto convexo en un espacio vectorial topológico real o complejo está conectado por caminos, por lo tanto conectado.

Un conjunto $C$ es estrictamente convexo si cada punto en el segmento de línea que conecta $x$ y $y$ que no sean los extremos está dentro del interior topológico de $C$ . Un subconjunto convexo cerrado es estrictamente convexo si y solo si cada uno de sus puntos límite es un punto extremo.

Un conjunto $C$ es absolutamente convexo si es convexo y equilibrado.

Los subconjuntos convexos de $R$ (el conjunto de números reales) son los intervalos y los puntos de $R$ . Algunos ejemplos de subconjuntos convexos del plano euclidiano son polígonos regulares sólidos, triángulos sólidos e intersecciones de triángulos sólidos. Algunos ejemplos de subconjuntos convexos de un espacio tridimensional euclidiano son los sólidos de Arquímedes y los sólidos platónicos. Los poliedros de Kepler-Poinsot son ejemplos de conjuntos no convexos.

Conjunto no convexo

Un conjunto que no es convexo se llama conjunto no convexo. Un polígono que no es un polígono convexo a veces se denomina polígono cóncavo, y algunas fuentes generalmente usan el término conjunto cóncavo para referirse a un conjunto no convexo, pero la mayoría de las autoridades prohíben este uso.

El complemento de un conjunto convexo, como el epígrafe de una función cóncava, a veces se denomina conjunto convexo inverso, especialmente en el contexto de la optimización matemática.

Propiedades

Dados $r$ puntos $u 1,..., u r$ en un conjunto convexo $S$ y $r$ números no negativos $λ 1,..., λ r$ tal que $λ 1 +... + λ r = 1$ , la combinación afín

{displaystyle sum _{k=1}^{r}lambda _{k}u_{k}}

S

r = 2

Tal combinación afín se llama combinación convexa de $u 1,..., u r$ .

Intersecciones y uniones

La colección de subconjuntos convexos de un espacio vectorial, un espacio afín o un espacio euclidiano tiene las siguientes propiedades:

El conjunto vacío y todo el espacio son convexos.
La intersección de cualquier colección de conjuntos convex es convex.
El sindicato de una secuencia de conjuntos de convex es convex, si forman una cadena no-disminución para la inclusión. Para esta propiedad, la restricción a cadenas es importante, ya que la unión de dos conjuntos convexo no necesita Sé convex.

Conjuntos convexos cerrados

Los conjuntos convexos cerrados son conjuntos convexos que contienen todos sus puntos límite. Se pueden caracterizar como las intersecciones de medios espacios cerrados (conjuntos de puntos en el espacio que se encuentran sobre ya un lado de un hiperplano).

De lo que se acaba de decir, es claro que tales intersecciones son convexas, y también serán conjuntos cerrados. Para demostrar lo contrario, es decir, cada conjunto convexo cerrado puede representarse como tal intersección, se necesita el teorema del hiperplano de apoyo en la forma que para un conjunto convexo cerrado dado $C$ y punto $P$ fuera de él, hay un semiespacio cerrado $H$ que contiene $C$ y no P. El teorema del hiperplano de apoyo es un caso especial del teorema de análisis funcional de Hahn-Banach.

Conjuntos convexos y rectángulos

Sea $C$ un cuerpo convexo en el plano (un conjunto convexo cuyo interior no está vacío). Podemos inscribir un rectángulo r en $C$ tal que una copia homotética R de r se circunscribe a $C$ . La relación de homotecia positiva es como máximo 2 y:

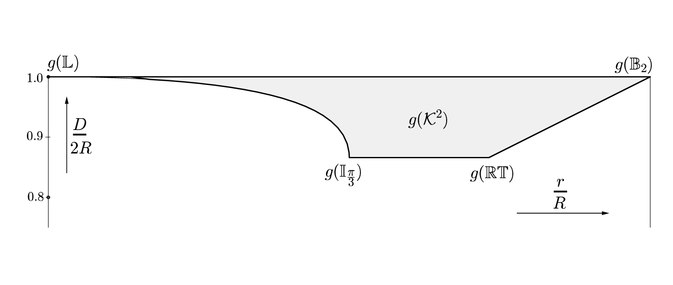
{displaystyle {tfrac {1}{2}}cdot operatorname {Area} (R)leq operatorname {Area} (C)leq 2cdot operatorname {Area} (r)}

Diagramas de Blaschke-Santaló

El set ${displaystyle {mathcal {K}}^{2}}$ de todos los cuerpos convexos plano pueden ser parametizados en términos del diámetro del cuerpo convexo D, su inradius r (el círculo más grande contenido en el cuerpo convexo) y su circunradius R (el círculo más pequeño que contiene el cuerpo convexo). De hecho, este conjunto puede ser descrito por el conjunto de desigualdades dadas por

{displaystyle 2rleq Dleq 2R}

{displaystyle Rleq {frac {sqrt {3}}{3}}D}

{displaystyle r+Rleq D}

{displaystyle D^{2}{sqrt {4R^{2}-D^{2}}}leq 2R(2R+{sqrt {4R^{2}-D^{2}}})}

R 2

rRDRrDR

Blaschke-Santalór, D, R) diagrama para los cuerpos de convexo plano.

mathbb {L}

denota el segmento de línea,

{displaystyle mathbb {I} _{frac {pi }{3}}}

el triángulo equilátero,

{displaystyle mathbb {RT} }

el triángulo Reuleaux y

{displaystyle mathbb {B} _{2}}

el círculo de la unidad.

Alternativamente, el conjunto ${displaystyle {mathcal {K}}^{2}}$ también se puede parametrizar por su ancho (la distancia más pequeña entre cualquier dos hiperplanos de soporte paralelo diferentes), perímetro y área.

Otras propiedades

Vamos X ser un espacio vectorial topológico y $Csubseteq X$ Sé convex.

${displaystyle operatorname {Cl} C}$ y ${displaystyle operatorname {Int} C}$ son ambos convex (es decir, el cierre y el interior de conjuntos convex son convex).
Si ${displaystyle ain operatorname {Int} C}$ y ${displaystyle bin operatorname {Cl} C}$ entonces ${displaystyle [a,b[,subseteq operatorname {Int} C}$ (donde) $<math alttext="{displaystyle [a,b[,:=left{(1-r)a+rb:0leq r[a,b[:={}()1- - r)a+rb:0\leq \leq r.1}{displaystyle [a,b[,:=left{(1-r)a+rb:0leq r made1right} <img alt="{displaystyle [a,b[,:=left{(1-r)a+rb:0leq r$ ).
Si Int⁡ ⁡ Cل ل ∅ ∅ {displaystyle operatorname Cneq emptyset ${displaystyle operatorname {Int} Cneq emptyset }$ entonces:
- ${displaystyle operatorname {cl} left(operatorname {Int} Cright)=operatorname {Cl} C}$ , y
- ${displaystyle operatorname {Int} C=operatorname {Int} left(operatorname {Cl} Cright)=C^{i}}$ , donde ${displaystyle C^{i}}$ es el interior algebraico de C.

Cascos convexos y sumas de Minkowski

Cascos convexos

Cada subconjunto $A$ del espacio vectorial está contenido dentro de un conjunto convexo más pequeño (llamado el casco convexo de $A$ ), es decir, la intersección de todos los conjuntos convexos que contienen $A$ . El operador de casco convexo Conv() tiene las propiedades características de un operador de casco:

extensiva: $S \subseteq Conv(S)$ ,
no disminución: $S \subseteq T$ implica que $Conv(S \subseteq Conv(T)$ , y
idempotente: $Conv(Conv(S) = Conv(S)$ .

La operación de casco convexo es necesaria para que el conjunto de conjuntos convexos forme una red, en la que la "unión" la operación es el casco convexo de la unión de dos conjuntos convexos

{displaystyle operatorname {Conv} (S)vee operatorname {Conv} (T)=operatorname {Conv} (Scup T)=operatorname {Conv} {bigl (}operatorname {Conv} (S)cup operatorname {Conv} (T){bigr)}.}

Adición de Minkowski

Minkowski adición de conjuntos. La suma de los cuadrados Q₁=[0,1]² y Q₂=[1,2]² es el cuadrado Q₁+Q₂=[1,3]².

En un espacio vectorial real, la suma de Minkowski de dos conjuntos (no vacíos), $S 1$ y $S 2$ , se define como el conjunto $S 1 + S 2$ formado por la suma de vectores elemento-sabio del sumando -conjuntos

{displaystyle S_{1}+S_{2}={x_{1}+x_{2}:x_{1}in S_{1},x_{2}in S_{2}}.}

Minkowski sum

S n

{displaystyle sum _{n}S_{n}=left{sum _{n}x_{n}:x_{n}in S_{n}right}.}

Para la suma de Minkowski, el conjunto cero ${0}$ que contiene solo el vector cero $0$ tiene especial importancia: Para todo subconjunto no vacío S de un espacio vectorial

{displaystyle S+{0}=S;}

{0}

Cascos convexos de sumas de Minkowski

La suma de Minkowski se comporta bien con respecto a la operación de tomar cascos convexos, como lo muestra la siguiente proposición:

Sean $S 1, S 2$ subconjuntos de un espacio vectorial real, la envolvente convexa de su suma de Minkowski es la suma de Minkowski de sus envolventes convexas

{displaystyle operatorname {Conv} (S_{1}+S_{2})=operatorname {Conv} (S_{1})+operatorname {Conv} (S_{2}).}

Este resultado es más general para cada colección finita de conjuntos no vacíos:

{displaystyle {text{Conv}}left(sum _{n}S_{n}right)=sum _{n}{text{Conv}}left(S_{n}right).}

En terminología matemática, las operaciones de suma de Minkowski y de formación de cascos convexos son operaciones de conmutación.

Sumas de Minkowski de conjuntos convexos

La suma de Minkowski de dos conjuntos convexos compactos es compacta. La suma de un conjunto convexo compacto y un conjunto convexo cerrado es cerrada.

El siguiente teorema famoso, probado por Dieudonné en 1966, da una condición suficiente para que la diferencia de dos subconjuntos convexos cerrados sea cerrada. Utiliza el concepto de un cono de recesión de un subconjunto convexo no vacío S, definido como:

{displaystyle operatorname {rec} S=left{xin X,:,x+Ssubseteq Sright},}

{displaystyle 0in X}

{displaystyle S+operatorname {rec} S=S}

{displaystyle operatorname {rec} S}

{displaystyle s_{0}in S}

0}t(S-s_{0}).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">rec⁡ ⁡ S=⋂ ⋂ t■0t()S− − s0).{displaystyle operatorname {rec} S=bigcap _{t confianza0}t(S-s_{0}). }0}t(S-s_{0}).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d4d444c57a3953929f3d56e6fb432880f2853503" style="vertical-align: -3.005ex; width:20.823ex; height:5.509ex;"/>

Theorem (Dieudonné). Vamos A y B ser subconjuntos no vacíos, cerrados y convexos de un espacio vectorial topológico localmente convexo tal que ${displaystyle operatorname {rec} Acap operatorname {rec} B}$ es un subespacio lineal. Si A o B es localmente compacto entonces A−B está cerrado.

Generalizaciones y extensiones para convexidad

La noción de convexidad en el espacio euclidiano puede generalizarse modificando la definición en unos u otros aspectos. El nombre común "convexidad generalizada" se utiliza, porque los objetos resultantes conservan ciertas propiedades de los conjuntos convexos.

Conjuntos estrella-convexos (en forma de estrella)

Sea $C$ un conjunto en un espacio vectorial real o complejo. $C$ es estrella convexa (en forma de estrella) si existe una $x 0$ en $C$ tal que la línea segmento desde $x 0$ hasta cualquier punto $y$ en $C$ está contenido en $C$ . Por lo tanto, un conjunto convexo no vacío siempre es convexo en estrella, pero un conjunto convexo en estrella no siempre es convexo.

Convexidad ortogonal

Un ejemplo de convexidad generalizada es la convexidad ortogonal.

Un conjunto $S$ en el espacio euclidiano se llama ortogonalmente convexo u orto- convexo, si cualquier segmento paralelo a cualquiera de los ejes de coordenadas que conectan dos puntos de $S$ se encuentra totalmente dentro de S. Es fácil demostrar que una intersección de cualquier colección de conjuntos ortoconvexos es ortoconvexa. Algunas otras propiedades de los conjuntos convexos también son válidas.

Geometría no euclidiana

La definición de un conjunto convexo y un casco convexo se extiende naturalmente a las geometrías que no son euclidianas al definir un conjunto geodésicamente convexo como aquel que contiene las geodésicas que unen dos puntos cualesquiera del conjunto.

Topología de orden

La convexidad se puede extender para un conjunto totalmente ordenado $X$ dotado de la topología de orden.

Sea $Y \subseteq X$ . El subespacio $Y$ es un conjunto convexo si para cada par de puntos $a, b$ en $Y$ tal que $a \leq b$ , el intervalo $[a, b] = {x \in X | a \leq x \leq b}$ está contenido en $Y$ . Es decir, $Y$ es convexo si y solo si para todos $a, b$ en $Y$ , $a \leq b$ implica $[a, b] \subseteq Y$ .

Un conjunto convexo no es conexo en general: el subespacio {1,2,3} en $Z$ , que es a la vez convexo y no conectado.

Espacios de convexidad

La noción de convexidad puede generalizarse a otros objetos, si se seleccionan ciertas propiedades de convexidad como axiomas.

Dado un conjunto $X$ , una convexidad sobre el estilo $X$ es una colección $𝒞$ de subconjuntos del estilo $X$ satisfaciendo los siguientes axiomas:

El set vacío y $X$ están dentro $C$
La intersección de cualquier colección de $C$ está dentro $C$ .
La unión de una cadena (con respecto a la relación de inclusión) de elementos de $C$ está dentro $C$ .

Los elementos de $𝒞$ se denominan conjuntos convexos y el par $(X, 𝒞)$ se denomina espacio de convexidad. Para la convexidad ordinaria, se cumplen los dos primeros axiomas y el tercero es trivial.

Para una definición alternativa de convexidad abstracta, más adecuada para la geometría discreta, consulte las geometrías convexas asociadas con antimatroides.

Contenido relacionado

Más resultados...