Conjunto contable

ImprimirCitar

En matemáticas, un conjunto es contable si es finito o se puede hacer en correspondencia biunívoca con el conjunto de los números naturales. De manera equivalente, un conjunto es contable si existe una función inyectiva de él a los números naturales; esto significa que cada elemento del conjunto puede estar asociado a un único número natural, o que los elementos del conjunto pueden contarse uno a la vez, aunque la cuenta puede no terminar nunca debido a la infinidad de elementos.

En términos más técnicos, asumiendo el axioma de elección contable, un conjunto es contable si su cardinalidad (su número de elementos) no es mayor que la de los números naturales. Un conjunto contable que no es finito se dice infinito contable.

El concepto se atribuye a Georg Cantor, quien demostró la existencia de conjuntos incontables, es decir, conjuntos que no son contables; por ejemplo el conjunto de los números reales.

Una nota sobre la terminología

Aunque los términos "contable" y "contablemente infinito" como se definen aquí son bastante comunes, la terminología no es universal. Un estilo alternativo usa contable para referirse a lo que aquí se llama contablemente infinito, y a lo sumo contable para referirse a lo que aquí se llama contable. Para evitar la ambigüedad, uno puede limitarse a los términos "como máximo contable" y "contablemente infinito", aunque con respecto a la concisión esto es lo peor de ambos mundos. Se recomienda al lector que verifique la definición en uso cuando encuentre el término "contable" en la literatura.

También se pueden utilizar los términos enumerable y enumerable, p. refiriéndose a contable e infinito contable respectivamente, pero como las definiciones varían, se recomienda una vez más al lector que verifique la definición en uso.

Definición

La definición más concisa es en términos de cardenalidad. Un juego ${displaystyle S.$ es contable si su cardenalidad ${displaystyle Silencioso$ es menor o igual a ${displaystyle aleph _{0}$ (aleph-null), la cardinalidad del conjunto de números naturales ${displaystyle mathbb {N} ={0,1,2,3,ldots}$ . Un juego ${displaystyle S.$ es contablemente infinito si ${displaystyle Наль вальный нельсь ¿Qué?$ . Un juego incontable si no es contable, es decir, su cardenalidad es mayor que ${displaystyle aleph _{0}$ ; se remite al lector a un conjunto incontable para su ulterior discusión.

Para cada juego ${displaystyle S.$ , las siguientes proposiciones son equivalentes:

${displaystyle S.$ es contable.
Existe una función inyectable de $S$ a ${displaystyle mathbb {N}$ .
${displaystyle S.$ está vacío o existe una función subjetiva de ${displaystyle mathbb {N}$ a ${displaystyle S.$ .
Existe una cartografía bijeactiva entre ${displaystyle S.$ y un subconjunto ${displaystyle mathbb {N}$ .
${displaystyle S.$ es finito o contablemente infinito.

Del mismo modo, las siguientes proposiciones son equivalentes:

${displaystyle S.$ es contablemente infinito.
Hay un mapeo inyectable y subjetivo (y por lo tanto bijetivo) entre ${displaystyle S.$ y ${displaystyle mathbb {N}$ .
${displaystyle S.$ tiene una correspondencia única con ${displaystyle mathbb {N}$ .
Los elementos de ${displaystyle S.$ se puede organizar en una secuencia infinita ${fnMicrosoft Sans Serif}$ , donde ${displaystyle A_{i}$ es distinto ${displaystyle a_{j}$ para ${displaystyle ineq j}$ y todos los elementos ${displaystyle S.$ está lista.

Historia

En 1874, en su primer artículo de teoría de conjuntos, Cantor demostró que el conjunto de los números reales es incontable, demostrando así que no todos los conjuntos infinitos son contables. En 1878, utilizó correspondencias uno a uno para definir y comparar cardinalidades. En 1883, amplió los números naturales con sus ordinales infinitos y usó conjuntos de ordinales para producir una infinidad de conjuntos que tienen diferentes cardinalidades infinitas.

Introducción

A set es una colección de elementos, y puede ser descrito de muchas maneras. Una manera es simplemente enumerar todos sus elementos; por ejemplo, el conjunto consistente en los enteros 3, 4 y 5 puede ser denotado {3, 4, 5}, llamado forma de lista. Esto sólo es eficaz para pequeños conjuntos, sin embargo; para conjuntos más grandes, esto sería mucho tiempo y propensa a errores. En lugar de enumerar cada elemento, a veces una elipsis ("...") se utiliza para representar muchos elementos entre el elemento inicial y el elemento final en un conjunto, si el escritor cree que el lector puede adivinar fácilmente lo que... representa; por ejemplo, {1, 2, 3,..., 100} presumiblemente denota el conjunto de enteros de 1 a 100. Aun en este caso, sin embargo, sigue siendo posible para enumerar todos los elementos, porque el número de elementos en el conjunto es finito. Si numeramos los elementos del set 1,2, y así sucesivamente, hasta ${displaystyle n}$ , esto nos da la definición habitual de "sets of size ${displaystyle n}$ ".

Cartografía bijetiva del entero a números incluso

Algunos juegos son infinito; estos conjuntos tienen más que ${displaystyle n}$ elementos ${displaystyle n}$ es cualquier entero que se puede especificar. (No importa cuán grande sea el entero especificado ${displaystyle n}$ es, como ${displaystyle n=10^{1000}$ , conjuntos infinitos tienen más que ${displaystyle n}$ elementos.) Por ejemplo, el conjunto de números naturales, denotables por {0, 1, 2, 3, 4, 5,...}, tiene infinitamente muchos elementos, y no podemos utilizar ningún número natural para dar su tamaño. Puede parecer natural dividir los conjuntos en diferentes clases: juntar todos los conjuntos que contienen un elemento; todos los conjuntos que contienen dos elementos juntos;...; finalmente, juntar todos los conjuntos infinitos y considerarlos que tienen el mismo tamaño. Esta visión funciona bien para conjuntos contablemente infinitos y fue la suposición prevaleciente antes del trabajo de Georg Cantor. Por ejemplo, hay infinitamente muchos números enteros extraños, infinitamente muchos incluso enteros, y también infinitamente muchos enteros en general. Podemos considerar que todos estos conjuntos tienen el mismo tamaño porque podemos organizar cosas tales que, por cada entero, hay un entero diferente:

{displaystyle ldots ¡Derecho! !-!4,,-!1! ! !0,,1! !2, ,2!derecha !4,cdots }

{displaystyle nrightarrow 2n}

correspondencia de uno a unobijecióncontablemente infinito

{displaystyle aleph _{0}

Georg Cantor demostró que no todos los conjuntos infinitos son contablemente infinitos. Por ejemplo, los números reales no se pueden poner en correspondencia biunívoca con los números naturales (enteros no negativos). El conjunto de los números reales tiene mayor cardinalidad que el conjunto de los números naturales y se dice que es incontable.

Resumen formal

Por definición, un conjunto ${displaystyle S.$ es contable si existe una bijección entre ${displaystyle S.$ y un subconjunto de los números naturales ${displaystyle mathbb {N} ={0,1,2,dots}$ . Por ejemplo, definir la correspondencia

a ↔ 1, b ↔ 2, c ↔ 3

Desde cada elemento ${displaystyle S={a,b,c}$ está emparejado con Precisamente uno elemento ${displaystyle {1,2,3}}$ , y viceversa, esto define una bijeción, y muestra que ${displaystyle S.$ es contable. Del mismo modo podemos mostrar todos los conjuntos finitos son contables.

En cuanto al caso de conjuntos infinitos, un conjunto ${displaystyle S.$ es contablemente infinito si hay una bijeción entre ${displaystyle S.$ y todos ${displaystyle mathbb {N}$ . Como ejemplos, considere los conjuntos ${displaystyle A={1,2,3,dots }$ , el conjunto de enteros positivos, y ${displaystyle B={0,2,4,6,dots }$ , el conjunto de incluso números enteros. Podemos mostrar estos conjuntos son contablemente infinitos al mostrar una bijeción a los números naturales. Esto se puede lograr utilizando las asignaciones n Administración n+1 y n ↔ 2nAsí que

0 ↔ 1, 1 ↔ 2, 2 ↔ 3, 3 ↔ 3, 3 ↔ 4, 4 ↔ 5,...

0 ↔ 0, 1 ↔ 2, 2 ↔ 4, 3 ↔ 4, 3 ↔ 6, 4 ↔ 8,...

Todo conjunto infinito contable es contable, y todo conjunto contable infinito es infinito contable. Además, cualquier subconjunto de los números naturales es contable y, de manera más general:

Theorem—Un subconjunto de un conjunto contable es contable.

El conjunto de todos los pares ordenados de números naturales (el producto cartesiano de dos conjuntos de números naturales, ${displaystyle mathbb {N} times mathbb {N}$ es contablemente infinito, como se puede ver siguiendo un camino como el de la imagen:

La función de emparejamiento Cantor asigna un número natural a cada par de números naturales

El mapeo resultante procede de la siguiente manera:

0 (0, 0), 1, (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0),...

Este mapeo cubre todos esos pares ordenados.

Esta forma de cartografía triangular se generaliza recursivamente a ${displaystyle n}$ -tuples de números naturales, es decir, ${displaystyle (a_{1},a_{2},a_{3},dotsa_{n}}$ Donde ${displaystyle A_{i}$ y ${displaystyle n}$ son números naturales, mediante el mapeo repetidamente los dos primeros elementos de un ${displaystyle n}$ - tropezar con un número natural. Por ejemplo, (0, 2, 3) se puede escribir como ((0, 2), 3). Luego (0, 2) mapas a 5 así ((0, 2), 3) mapas a (5, 3), luego (5, 3) mapas a 39. Desde un 2-tuple diferente, que es un par como (a, b), mapas a un número natural diferente, una diferencia entre dos n-tuples por un solo elemento es suficiente para asegurar que los n-tuples se mapee a diferentes números naturales. Entonces, una inyección del conjunto de ${displaystyle n}$ -tuples al conjunto de números naturales ${displaystyle mathbb {N}$ está probado. Para el conjunto de ${displaystyle n}$ -tuples realizados por el producto cartesiano de muchos conjuntos finitos, cada elemento en cada tupla tiene la correspondencia a un número natural, por lo que cada tupla puede ser escrito en números naturales entonces la misma lógica se aplica para probar el teorema.

Theorem—El producto cartesiano de finitos muchos conjuntos contables es contable.

El conjunto de todos los enteros ${displaystyle mathbb {Z}$ y el conjunto de todos los números racionales ${displaystyle mathbb {Q}$ puede parecer intuitivamente mucho más grande que ${displaystyle mathbb {N}$ . Pero la apariencia puede ser engañosa. Si un par se trata como numerador y denominador de una fracción vulgar (una fracción en forma de ${displaystyle a/b}$ Donde ${displaystyle a}$ y ${displaystyle bneq 0}$ son enteros), entonces por cada fracción positiva, podemos llegar a un número natural distinto correspondiente a él. Esta representación también incluye los números naturales, ya que cada número natural ${displaystyle n}$ es también una fracción ${displaystyle n/1}$ . Así podemos concluir que hay exactamente tantos números racionales positivos como hay números enteros positivos. Esto también es cierto para todos los números racionales, como se puede ver a continuación.

Theorem— ${displaystyle mathbb {Z}$ (el conjunto de todos los enteros) y ${displaystyle mathbb {Q}$ (el conjunto de todos los números racionales) son contables.

De manera similar, el conjunto de números algebraicos es contable.

A veces más de una asignación es útil: un conjunto ${displaystyle A}$ para ser mostrado como contable es uno a uno mapeado (inyección) a otro conjunto ${displaystyle B}$ , entonces ${displaystyle A}$ es probado como contable si ${displaystyle B}$ es uno a uno mapeado al conjunto de números naturales. Por ejemplo, el conjunto de números racionales positivos puede ser fácilmente mapeado uno a uno al conjunto de pares de números naturales (2-tuples) porque ${displaystyle p/q}$ mapas a ${displaystyle (p,q)}$ . Dado que el conjunto de pares de números naturales es uno a uno mapeado (realmente una correspondencia o bijección) al conjunto de números naturales como se muestra anteriormente, el conjunto de número racional positivo se demuestra como contable.

Theorem—Cualquier unión finita de conjuntos contables es contable.

Con la previsión de saber que hay conjuntos incontables, podemos preguntarnos si este último resultado puede llevarse más lejos o no. La respuesta es "sí" y "no", podemos extenderlo, pero necesitamos asumir un nuevo axioma para hacerlo.

Theorem—(Asumiendo el axioma de la opción contable) La unión de muchos conjuntos contables es contable.

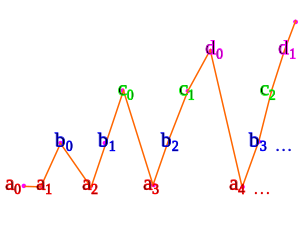
Por ejemplo, dados conjuntos contables ${displaystyle {textbf},{textbf {b},{textbf {c}},dots }$

Enumeración para número contable de conjuntos contables

Usando una variante de la enumeración triangular que vimos arriba:

a₀ mapas a 0
a₁ mapas a 1
b₀ mapas a 2
a₂ mapas a 3
b₁ mapas a 4
c₀ mapas a 5
a₃ mapas a 6
b₂ mapas a 7
c₁ mapas a 8
d₀ mapas a 9
a₄ mapas a 10
...

Esto solo funciona si los sets ${displaystyle {textbf},{textbf {b},{textbf {c}},dots }$ están descompuestos. Si no, entonces la unión es aún más pequeña y es por lo tanto también contable por un teorema anterior.

Necesitamos el axioma de la opción contable para indexar Todos los conjuntos ${displaystyle {textbf},{textbf {b},{textbf {c}},dots }$ simultáneamente.

Theorem—El conjunto de todas las secuencias de longitud finita de los números naturales es contable.

Este conjunto es la unión de las secuencias de longitud 1, las secuencias de longitud 2, las secuencias de longitud 3, cada una de las cuales es un conjunto contable (producto cartesiano finito). Entonces estamos hablando de una unión contable de conjuntos contables, que es contable por el teorema anterior.

Theorem—El conjunto de todos los subconjuntos finitos de los números naturales es contable.

Los elementos de cualquier subconjunto finito se pueden ordenar en una secuencia finita. Solo hay secuencias finitas numerables, por lo que también hay subconjuntos finitos numerables.

Theorem—Vamos ${displaystyle S.$ y ${displaystyle T}$ ser sets.

Si la función ${displaystyle f:Sto T}$ es inyectable y ${displaystyle T}$ es contable entonces ${displaystyle S.$ es contable.
Si la función ${displaystyle g:Sto T}$ es subjetivo y ${displaystyle S.$ es contable entonces ${displaystyle T}$ es contable.

Estos se derivan de las definiciones de conjunto contable como funciones inyectivas/sobreyectivas.

Teorema de Cantor afirma que si ${displaystyle A}$ es un conjunto y ${displaystyle {mathcal {}(A)}$ es su conjunto de poder, es decir, el conjunto de todos los subconjuntos de ${displaystyle A}$ , entonces no hay función subjetiva de ${displaystyle A}$ a ${displaystyle {mathcal {}(A)}$ . Una prueba se da en el teorema del artículo Cantor. Como consecuencia inmediata de esto y del Teorema Básico arriba tenemos:

Proposición—El set ${displaystyle {mathcal {fn} {fnMithbb}}$ no es contable; es decir, es incontable.

Para una elaboración de este resultado, vea el argumento diagonal de Cantor.

El conjunto de números reales es incontable, al igual que el conjunto de todas las sucesiones infinitas de números naturales.

El modelo mínimo de la teoría de conjuntos es contable

Si hay un conjunto que es un modelo estándar (ver modelo interno) de la teoría de conjuntos ZFC, entonces hay un modelo estándar mínimo (ver Universo construible). El teorema de Löwenheim-Skolem se puede utilizar para demostrar que este modelo mínimo es contable. El hecho de que la noción de "incontabilidad" tiene sentido incluso en este modelo, y en particular que este modelo M contiene elementos que son:

subconjuntos de M, por lo tanto contable,
pero incontable desde el punto de vista M,

fue visto como paradójico en los primeros días de la teoría de conjuntos, consulte la paradoja de Skolem para obtener más información.

El modelo estándar mínimo incluye todos los números algebraicos y todos los números trascendentales efectivamente computables, así como muchos otros tipos de números.

Pedidos totales

Los conjuntos contables se pueden ordenar totalmente de varias maneras, por ejemplo:

Bien ordenados (ver también número ordinal):
- El orden habitual de números naturales (0, 1, 2, 3, 4, 5,...)
- Los enteros en el orden (0, 1, 2, 3,...; −1, −2, −3,...)
Otros asuntosno bien órdenes:
- El orden habitual de los enteros (..., −3, −2, −1, 0, 1, 2, 3,...)
- El orden habitual de los números racionales (no se puede escribir explícitamente como una lista ordenada!)

En ambos ejemplos de órdenes de pozo aquí, cualquier subconjunto tiene un elemento mínimo; y en ambos ejemplos de órdenes no correctas, algunos subconjuntos no tienen un menor elemento. Esta es la definición clave que determina si un pedido total es también un pedido de pozo.

Contenido relacionado

Más resultados...