Compuesto de politopo
En geometría, un compuesto poliédrico es una figura que se compone de varios poliedros que comparten un centro común. Son los análogos tridimensionales de compuestos poligonales como el hexagrama.
Los vértices exteriores de un compuesto se pueden conectar para formar un poliedro convexo llamado casco convexo. Un compuesto es una faceta de su casco convexo.
Otro poliedro convexo está formado por el pequeño espacio central común a todos los miembros del compuesto. Este poliedro se puede utilizar como núcleo para un conjunto de estelaciones.
Compuestos regulares
Un compuesto poliédrico regular se puede definir como un compuesto que, como un poliedro regular, es transitivo de vértice, transitivo de borde y transitivo de cara. A diferencia del caso de los poliedros, esto no equivale a que el grupo de simetría actúe transitivamente sobre sus banderas; el compuesto de dos tetraedros es el único compuesto regular con esa propiedad. Hay cinco compuestos regulares de poliedros:
| Compuesto ordinario (Símbolo de Coxeter) | Imagen | Spherical | Convex hull | Base común | Grupo de Symmetry | Subgrupo restricción a uno constituyente | Compuesto doble-regular |
|---|---|---|---|---|---|---|---|
| Dos tetrahedra {4,3}[2{3,3} {3,4} |  |  | Cube | Octahedron | *432 [4,3] Oh | *332 [3,3] Td | Dos tetrahedra |
| Cinco tetrahedra {5,3} {5{3,3}} {3,5} {3}} {3}} {3}} {3}}} {3}}} {3}}}} {3}}}}} {3}}}}}} {3}}}}}} {3}}}}}}} {3}}}}}} {3}}}}}}}} {3}}}}}}}}}}}}}}}}}}} {3}}}}}}}}}} {3}}}}} {3}}}}}}} {3}}}}} {3}}}} {3}}}}}}}}}}}}}}}}}}}}} {3} {3}}}}} {3}}}}}} {3}}} {3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} |  |  | Dodecahedron | Icosahedron | 532 [5,3]+ I | 332 [3,3]+ T | Chiral twin (Enantiomorfo) |
| Diez tetrahedra 2{5,3}[10{3,3}]2{3,5} |  |  | Dodecahedron | Icosahedron | *532 [5,3] Ih | 332 [3,3] T | Diez tetrahedra |
| Cinco cubos 2{5,3}[5{4,3}] |  |  | Dodecahedron | Triacontahedron Rhombic | *532 [5,3] Ih | 3*2 [3,3] Th | Cinco octahedra |
| Cinco octahedra [5{3,4}]2{3,5} |  |  | Icosidodecahedron | Icosahedron | *532 [5,3] Ih | 3*2 [3,3] Th | Cinco cubos |
El más conocido es el compuesto regular de dos tetraedros, a menudo llamado stella octangula, un nombre que le dio Kepler. Los vértices de los dos tetraedros definen un cubo, y la intersección de los dos define un octaedro regular, que comparte los mismos planos faciales que el compuesto. Así, el compuesto de dos tetraedros es una estelación del octaedro y, de hecho, la única estelación finita del mismo.
El compuesto regular de cinco tetraedros viene en dos versiones enantiomórficas, que juntas forman el compuesto regular de diez tetraedros. El compuesto regular de diez tetraedros también se puede construir con cinco Stellae octangulae.
Cada uno de los compuestos tetraédricos regulares es autodual o dual con respecto a su gemelo quiral; el compuesto regular de cinco cubos y el compuesto regular de cinco octaedros son duales entre sí.
Por lo tanto, los compuestos poliédricos regulares también pueden considerarse como compuestos regulares duales.
La notación de Coxeter para compuestos regulares se da en la tabla anterior, incorporando símbolos de Schläfli. El material dentro de los corchetes, [d{p,q}], denota los componentes del compuesto: d separar {p,q}'s. El material anterior a los corchetes indica la disposición de los vértices del compuesto: c{m,n}[d{p,q}] es un compuesto de d {p,q}'s compartiendo los vértices de {m,n} contados c veces. El material después de los corchetes indica la disposición de las facetas del compuesto: [d{p,q}] e{s,t} es un compuesto de d {p,q}'s compartiendo las caras de {s,t} contadas e veces. Estos pueden combinarse: así c{m,n}[d{p,q}]e{s,t} es un compuesto de d {p,q} comparte los vértices de {m,n} contados c veces y las caras de {s,t} contadas e veces. Esta notación se puede generalizar a compuestos en cualquier número de dimensiones.
Compuestos duales
Un compuesto dual está formado por un poliedro y su dual, dispuestos recíprocamente alrededor de una esfera media común, de modo que la arista de un poliedro se cruza con la arista dual del poliedro dual. Hay cinco compuestos duales de los poliedros regulares.
El núcleo es la rectificación de ambos sólidos. El casco es el dual de esta rectificación, y sus caras rómbicas tienen las aristas de intersección de los dos sólidos como diagonales (y tienen sus cuatro vértices alternos). Para los sólidos convexos, este es el casco convexo.
| Compuesto doble | Imagen | Hull | Core | Grupo de Symmetry |
|---|---|---|---|---|
| Dos tetrahedra (Completa de dos tetrahedra, octaedro estelar) |  | Cube | Octahedron | *432 [4,3] Oh |
| Cubo y octaedro (Completa de cubo y octaedro) |  | Rhombic dodecahedron | Cuboctahedron | *432 [4,3] Oh |
| Dodecahedron y icosahedron (Completa de dodecahedron y icosahedron) |  | Triacontahedron Rhombic | Icosidodecahedron | *532 [5,3] Ih |
| Pequeño dodecaedro estelar y gran dodecaedro (Completa de SD y GD) | ,_thick.png) | Medial rhombic triacontahedron (Convex: Icosahedron) | Dodecadodecahedron (Convex: Dodecahedron) | *532 [5,3] Ih |
| Gran icosahedro y gran dodecaedro estelar (Completa de gI y gsD) |  | Gran triacontahedron rhombic (Convex: Dodecahedron) | Great icosidodecahedron (Convex: Icosahedron) | *532 [5,3] Ih |
El tetraedro es autodual, por lo que el compuesto dual de un tetraedro con su dual es el octaedro estrellado regular.
Los compuestos duales octaédricos e icosaédricos son las primeras estelaciones del cuboctaedro y el icosidodecaedro, respectivamente.
El compuesto dual dodecaédrico estrellado pequeño (o dodecaédrico grande) tiene el dodecaedro grande completamente interior al dodecaedro estrellado pequeño.
Compuestos uniformes
En 1976, John Skilling publicó Compuestos uniformes de poliedros uniformes, que enumeró 75 compuestos (incluidos 6 como conjuntos prismáticos infinitos de compuestos, #20-#25) hechos de poliedros uniformes con simetría rotacional. (Cada vértice es transitivo de vértice y cada vértice es transitivo con todos los demás vértices). Esta lista incluye los cinco compuestos regulares anteriores. [1]
Los 75 compuestos uniformes se enumeran en la siguiente tabla. La mayoría se muestran coloreados singularmente por cada elemento poliedro. Algunos pares quirales de grupos de caras están coloreados por la simetría de las caras dentro de cada poliedro.
- 1-19: Misceláneas (4,5,6,9,17 son las 5 compuestos ordinarios)
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
- 20-25: Simetría prisma incrustada en simetría del prisma,
 |  |  |  |  |  |
- 26-45: Simetría prisma incrustada en simetría octaedral o icosahedral,
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
- 46-67: Simetría tetraedral incrustada en simetría octaedral o icosahedral,
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |
- 68-75: pares enantiomorfos
 |  |  |  |  |  |
 |  |
Otros compuestos
 |  |
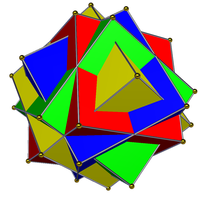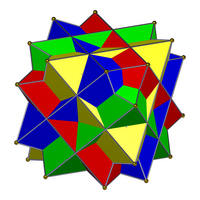| El compuesto de cuatro cubos (izquierda) no es un compuesto regular, ni un compuesto dual, ni un compuesto uniforme. Su doble, el compuesto de cuatro octahedra (derecha), es un compuesto uniforme. | |
- Compuesto de tres octahedra
- Compuesto de cuatro cubos
Dos poliedros que son compuestos pero que tienen sus elementos rígidamente bloqueados en su lugar son el icosidodecaedro complejo pequeño (compuesto de icosaedro y un gran dodecaedro) y el gran icosidodecaedro complejo (compuesto de un pequeño dodecaedro estrellado y un gran icosaedro). Si se generaliza la definición de poliedro uniforme, son uniformes.
La sección de pares de enantiomorfos en la lista de Skilling no contiene el compuesto de dos grandes dodecicosidodecaedros chatos, ya que las caras del pentagrama coincidirían. Eliminar las caras coincidentes da como resultado el compuesto de veinte octaedros.
Compuestos de 4 politopos
 |  |
| 75 {4,3,3} | 75 {3,3,4} |
|---|
En 4 dimensiones, hay una gran cantidad de compuestos regulares de politopos regulares. Coxeter enumera algunos de estos en su libro Regular Polytopes. McMullen agregó seis en su artículo Nuevos compuestos regulares de 4 politopos.
Autoduales:
| Compuesto | Constituyente | Simmetría |
|---|---|---|
| 120 5 celdas | 5 celdas | [5,3,3], orden 14400 |
| 120 5 celdas(var) | 5 celdas | Orden 1200 |
| 720 5 celdas | 5 celdas | [5,3,3], orden 14400 |
| 5 24 celdas | 24 horas | [5,3,3], orden 14400 |
Pares dobles:
| Compuesto 1 | Compuesto 2 | Simmetría |
|---|---|---|
| 3 16 celdas | 3 tesseracts | [3,4,3], orden 1152 |
| 15 celdas | 15 tesseracts | [5,3,3], orden 14400 |
| 75 16 celdas | 75 tesseracts | [5,3,3], orden 14400 |
| 75 16 celdas(var) | 75 tesseracts(var) | Orden 600 |
| 300 16 celdas | 300 tesseracts | [5,3,3]+, orden 7200 |
| 600 celdas | 600 tesseracts | [5,3,3], orden 14400 |
| 25 24 celdas | 25 24 celdas | [5,3,3], orden 14400 |
Compuestos uniformes y duales con 4 politopos convexos:
| Compuesto 1 Vertex-transitive | Compuesto 2 Cell-transitive | Simmetría |
|---|---|---|
| 2 16 celdas | 2 tesseracts | [4,3,3], orden 384 |
| 100 24 celdas | 100 24 celdas | [5,3,3]+, orden 7200 |
| 200 celdas | 200 celdas | [5,3,3], orden 14400 |
| 5 600 celdas | 5 120 celdas | [5,3,3]+, orden 7200 |
| 10 600 celdas | 10 120 celdas | [5,3,3], orden 14400 |
| 25 24 celdas(var) | 25 24 celdas(var) | Orden 600 |
El superíndice (var) en las tablas anteriores indica que los compuestos etiquetados son distintos de los otros compuestos con el mismo número de constituyentes.
Compuestos con 4-politopos regulares en estrella
Compuestos de estrella autodual:
| Compuesto | Simmetría |
|---|---|
| 5 {5,5/2,5} | [5,3,3]+, orden 7200 |
| 10 {5,5/2,5} | [5,3,3], orden 14400 |
| 5 {5/2,5,5/2} | [5,3,3]+, orden 7200 |
| 10 {5/2,5,5/2} | [5,3,3], orden 14400 |
Pares duales de estrellas compuestas:
| Compuesto 1 | Compuesto 2 | Simmetría |
|---|---|---|
| 5 {3,5,5/2} | 5/2,5,3} | [5,3,3]+, orden 7200 |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], orden 14400 |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3]+, orden 7200 |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], orden 14400 |
| 5/2,3,5} | 5 {5,3,5/2} | [5,3,3]+, orden 7200 |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], orden 14400 |
Estrellas compuestas uniformes y duales:
| Compuesto 1 Vertex-transitive | Compuesto 2 Cell-transitive | Simmetría |
|---|---|---|
| 5 {3,3,5/2} | 5/2,3,3} | [5,3,3]+, orden 7200 |
| 10 {3,3.5/2} | 10 {5/2,3,3} | [5,3,3], orden 14400 |
Compuestos con duales
Puestos dobles:
| Compuesto | Constituyente | Simmetría |
|---|---|---|
| 2 5 celdas | 5 celdas | [[3,3]], orden 240 |
| 2 24 celdas | 24 horas | [[3,4,3]], orden 2304 |
| 1 tesseract, 1 16-cell | tesseract, 16 celdas | |
| 1 120 celdas, 1 600 celdas | 120 celdas, 600 celdas | |
| 2 grandes 120 celdas | grandes 120 celdas | |
| 2 grandes de 120 células estelares | de 120 células | |
| 1 icosahedral 120-cell, 1 pequeño estelar 120-cell | icosahedral 120-cell, pequeño estelar 120-cell | |
| 1 grand 120-cell, 1 gran 120-cell | grandes 120 células, gran estelar 120 células | |
| 1 grandes grandes 120-cell, 1 gran icosahedral 120-cell | grandes grandes 120 células, grandes icosahedral 120-cell | |
| 1 gran número estelar 120 celdas, 1 gran 600 celdas | grandes grandes de 120 celdas, grandes 600 celdas |
Teoría de grupos
En términos de teoría de grupos, si G es el grupo de simetría de un compuesto poliédrico, y el grupo actúa transitivamente sobre los poliedros (de modo que cada poliedro puede enviarse a cualquiera de los otros, como en compuestos uniformes), entonces si H es el estabilizador de un solo poliedro elegido, los poliedros se pueden identificar con el espacio de órbita G/H – la clase lateral gH corresponde a qué poliedro g envía el poliedro elegido.
Compuestos de mosaicos
Hay dieciocho familias de dos parámetros de teselaciones compuestas regulares del plano euclidiano. En el plano hiperbólico, se conocen cinco familias de un parámetro y diecisiete casos aislados, pero no se ha enumerado la totalidad de esta lista.
Las familias de compuestos euclidianos e hiperbólicos 2 {p,p} (4 ≤ p ≤ ∞, p un entero) son análogas a la esférica stella octangula, 2 {3,3}.
| Auto-dual | Duales | Auto-dual | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {Libertad: |
 |  |  |  |
| 3 {6,3} | 3 {3,6} | 3 ``¿Quién es? | |
 |  |  | |
Una familia conocida de panales compuestos euclidianos regulares en cualquier número de dimensiones es una familia infinita de compuestos de panales hipercúbicos, todos compartiendo vértices y caras con otro panal hipercúbico. Este compuesto puede tener cualquier número de panales hipercúbicos.
También hay compuestos para mosaicos dual-regular. Un ejemplo simple es el compuesto E2 de un mosaico hexagonal y su mosaico triangular dual, que comparte sus bordes con el mosaico trihexagonal deltoidal. Los compuestos euclidianos de dos panales hipercúbicos son regulares y regulares duales.
Contenido relacionado
Billy salvaje
John Woo
Horacio Walpole