Complejo de cadenas

En matemáticas, un complejo en cadena es una estructura algebraica que consta de una secuencia de grupos abelianos (o módulos) y una secuencia de homomorfismos entre grupos consecutivos de manera que la imagen de cada homomorfismo se incluye en el núcleo del siguiente. Asociado a un complejo de cadena está su homología, que describe cómo se incluyen las imágenes en los núcleos.

Un complejo cocadena es similar a un complejo cadena, excepto que sus homomorfismos están en dirección opuesta. La homología de un complejo cocadena se denomina cohomología.

En la topología algebraica, el complejo de cadena singular de un espacio topológico X se construye utilizando mapas continuos de un símplex a X, y los homomorfismos del complejo de cadena capturan cómo estos mapas se restringen al límite del símplex. La homología de este complejo de cadenas se denomina homología singular de X y es una invariante de uso común de un espacio topológico.

Los complejos de cadenas se estudian en álgebra homológica, pero se utilizan en varias áreas de las matemáticas, incluida el álgebra abstracta, la teoría de Galois, la geometría diferencial y la geometría algebraica. Se pueden definir de manera más general en categorías abelianas.

Definiciones

A complejo de cadena ()A∙ ∙ ,d∙ ∙ ){displaystyle (A_{bullet },d_{bullet }} es una secuencia de grupos o módulos abelianos... A₀, A₁, A₂, A₃, A₄,... conectado por homomorfismos (llamados operadores de fronteras o diferenciales) d_n: A_n → A_n−1, tal que la composición de cualquier dos mapas consecutivos es el mapa cero. Explícitamente, las diferencias satisfacen d_n ∘ d_{n+ 1} = 0, o con índices suprimidos, d² = 0. El complejo puede ser escrito como sigue.

⋯ ⋯ ←d0A0←d1A1←d2A2←d3A3←d4A4←d5⋯ ⋯ {displaystyle cdots {xleftarrow {fnK}A_{0}{xleftarrow {fnK}A_{1}{xleftarrow {fnK}A_{2}{xleftarrow {fnK}A_{3}{xleftarrow {fnK}A_{4}{xleftarrow {d_{5}}cdots }

El cochain complex ()A∙ ∙ ,d∙ ∙ ){displaystyle (A^{bullet },d^{bullet }} es la noción dual a un complejo de cadena. Consiste en una secuencia de grupos o módulos abelianos... A⁰, A¹, A², A³, A⁴,... conectado por homomorfismos dⁿ: Aⁿ → A^{n+ 1} satisfacción d^{n+ 1} ∘ dⁿ = 0. El complejo de cochain se puede escribir de forma similar al complejo de cadena.

⋯ ⋯ →d− − 1A0→d0A1→d1A2→d2A3→d3A4→d4⋯ ⋯ {displaystyle cdots {xrightarrow {fnK}A}{0}{xrightarrow {fnK}A}{1}{xrightarrow {cHFF}A}{2}{xrightarrow {fnK}A}{3}{xrightarrow {fnK}A}{4}{xrightarrow {d^{4}}cdots }

El índice n en A_n o A ⁿ se conoce como el grado (o dimensión). La diferencia entre los complejos de cadena y cocadena es que, en los complejos de cadena, los diferenciales disminuyen la dimensión, mientras que en los complejos de cocadena aumentan la dimensión. Todos los conceptos y definiciones de los complejos de cadena se aplican a los complejos de cocadena, excepto que seguirán esta convención diferente para la dimensión y, a menudo, a los términos se les dará el prefijo co-. En este artículo, se darán definiciones para cadenas complejas cuando no se requiera la distinción.

Un complejo de cadena acotada es aquel en el que casi todos los A_n son 0; es decir, un complejo finito extendido hacia la izquierda y hacia la derecha por 0. Un ejemplo es el complejo en cadena que define la homología simplicial de un complejo simplicial finito. Un complejo de cadenas está acotado por arriba si todos los módulos por encima de algún grado fijo N son 0, y está acotado por debajo si todos los módulos por debajo de algún grado fijo son 0. Claramente, un complejo está acotado tanto por arriba como por abajo si y solo si el complejo está acotado.

Los elementos de los grupos individuales de un complejo de (co)cadenas se denominan (co)cadenas. Los elementos del núcleo de d se denominan (co)ciclos (o elementos cerrados), y los elementos de la imagen de d se denominan (co)límites (o elementos exactos). Desde la definición del diferencial, todos los límites son ciclos. El n-ésimo (co)grupo de homología H_n ( Hⁿ) es el grupo de (co)ciclos módulo (co)fronteras en grado n, es decir,

Hn=ker⁡ ⁡ dn/imdn+1()Hn=ker⁡ ⁡ dn/imdn− − 1){displaystyle H_{n}=ker ♪ {n}/{mbox{im }d_{n+1}quad left(H^{n}=ker ¿Qué?

Secuencias exactas

Una secuencia exacta (o complejo exacto) es un complejo en cadena cuyos grupos de homología son todos cero. Esto significa que todos los elementos cerrados del complejo son exactos. Una sucesión exacta corta es una sucesión exacta acotada en la que sólo los grupos A_k, A_k+1, A_k+2 puede ser distinto de cero. Por ejemplo, el siguiente complejo de cadena es una secuencia exacta corta.

⋯ ⋯ →0→Z→× × pZ↠ ↠ Z/pZ→0→⋯ ⋯ {displaystyle cdots {xrightarrow {};0;{xrightarrow {};fnMitbf {Z};{xrightarrow {times p};mathbf {Z} twoheadrightarrow mathbf {Z} /pmathbf {Z} ;{xrightarrow {};0;{xrightarrow {}cdots }

En el grupo medio, los elementos cerrados son los elementos pZ; estos son claramente los elementos exactos en este grupo.

Mapas de cadenas

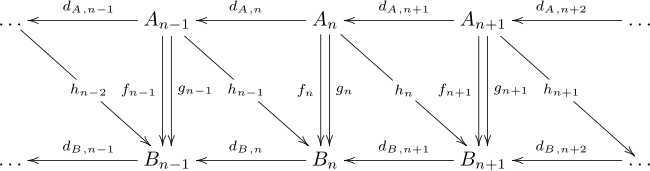
A cadena mapa f entre dos complejos de cadena ()A∙ ∙ ,dA,∙ ∙ ){displaystyle (A_{bullet },d_{A,bullet }} y ()B∙ ∙ ,dB,∙ ∙ ){displaystyle (B_{bullet },d_{B,bullet }} es una secuencia f∙ ∙ {displaystyle f_{bullet}} de homomorfismos fn:An→ → Bn{displaystyle ¿Qué? B_{n} para cada uno n que se comunica con los operadores de límites en los dos complejos de cadena, así dB,n∘ ∘ fn=fn− − 1∘ ∘ dA,n{displaystyle D_{B,n}circ F_{n}=f_{n-1}circ D_{A,n}. Esto está escrito en el siguiente diagrama conmutativo.

Un mapa de cadena envía ciclos a ciclos y límites a límites, e induce así un mapa sobre homología ()f∙ ∙ )Alternativa Alternativa :H∙ ∙ ()A∙ ∙ ,dA,∙ ∙ )→ → H∙ ∙ ()B∙ ∙ ,dB,∙ ∙ ){displaystyle (f_{bullet })_{*}:H_{bullet ♪,d_{A,bullet })derecha H_{bullet }(B_{bullet - Sí..

Un mapa continuo f entre espacios topológicos X e Y induce un mapa en cadena entre los complejos de cadena singulares de X y Y, y por lo tanto induce un mapa f_* entre la homología singular de X y Y también. Cuando X e Y son ambos iguales a la n-esfera, el mapa inducido por homología define el grado del mapa f.

El concepto de mapa de cadena se reduce al de frontera mediante la construcción del cono de un mapa de cadena.

Cadena de homotopía

Una homotopía de cadena ofrece una forma de relacionar dos mapas de cadena que inducen el mismo mapa en grupos de homología, aunque los mapas pueden ser diferentes. Dados dos complejos de cadena A y B, y dos mapas de cadena f, g: A → B, una homotopía en cadena es una secuencia de homomorfismos h_n: A_n → B_n+1 tal que hd_A + d_Bh = f − g. Los mapas se pueden escribir en un diagrama de la siguiente manera, pero este diagrama no es conmutativo.

El mapa hd_A + d_Bh se verifica fácilmente para inducir el mapa cero en la homología, para cualquier h. Inmediatamente se sigue que f y g inducen el mismo mapa en homología. Se dice que f y g son cadenas homotópicas (o simplemente homotópicas), y esta propiedad define una relación de equivalencia entre mapas de cadenas

Sean X e Y espacios topológicos. En el caso de homología singular, una homotopía entre mapas continuos f, g: X → Y induce una homotopía de cadena entre los mapas de cadena correspondientes a f y g. Esto muestra que dos mapas homotópicos inducen el mismo mapa en homología singular. El nombre "homotopía en cadena" está motivado por este ejemplo.

Ejemplos

Homología singular

Vamos X ser un espacio topológico. Define C_n()X) para natural n ser el grupo libre abeliano generado formalmente por singulares n-simplices en X, y definir el mapa de límites ∂ ∂ n:Cn()X)→ → Cn− − 1()X){displaystyle partial _{n}:C_{n}(X)to C_{n-1}(X)} para ser

∂ ∂ n:()σ σ :[v0,...... ,vn]→ → X)↦ ↦ ().. i=0n()− − 1)iσ σ :[v0,...... ,v^ ^ i,...... ,vn]→ → X){fnMicrosoft Sans Serif} {fn}fn}fnfn}n}n}n}n}n}nn}nn}nnn}nnn}nnn}nn}n}nnnn}nnhnnnnKnhnhnK]

donde el sombrero denota la omisión de un vértice. Es decir, el límite de un singular simplex es la suma alternada de restricciones a sus rostros. Se puede mostrar que ∂² = 0, así que ()C∙ ∙ ,∂ ∂ ∙ ∙ ){displaystyle (C_{bullet },partial _{bullet })} es un complejo de cadena; el singular homología H∙ ∙ ()X){displaystyle H_{bullet }(X)} es la homología de este complejo.

La homología singular es una invariante útil de los espacios topológicos hasta la equivalencia homotópica. El grupo de homología de grado cero es un grupo abeliano libre en las componentes de ruta de X.

Cohomología de De Rham

Las formas k diferenciales en cualquier variedad suave M forman un espacio vectorial real llamado Ω^k(M) bajo adición. La derivada exterior d asigna Ω^k(M) a Ω^k+1(M), y d² = 0 se sigue esencialmente de la simetría de las segundas derivadas, por lo que los espacios vectoriales de las formas k junto con la derivada exterior son un complejo cocadenario.

Ω Ω 0()M)→ → dΩ Ω 1()M)→ → Ω Ω 2()M)→ → Ω Ω 3()M)→ → ⋯ ⋯ {displaystyle Omega ^{0}(M) {fnMicrosoft Sans Serif} Omega ^{1}(M)to Omega ^{2}(M)to Omega ^{3}(M)to cdots }

La cohomología de este complejo se denomina cohomología de Rham de M. El grupo de homología en dimensión cero es isomorfo al espacio vectorial de funciones localmente constantes de M a R. Así, para una variedad compacta, este es el espacio vectorial real cuya dimensión es el número de componentes conexas de M.

Los mapas uniformes entre variedades inducen mapas en cadena y las homotopías uniformes entre mapas inducen homotopías en cadena.

Categoría de complejos de cadenas

Los complejos de cadenas de módulos K con mapas de cadenas forman una categoría Ch_K, donde K es un anillo conmutativo.

Si V = VAlternativa Alternativa {displaystyle {}} y W = WAlternativa Alternativa {displaystyle {}} son complejos de cadena, sus producto tensor V⊗ ⊗ W{displaystyle Votimes W} es un complejo de cadena con grado n elementos dados por

()V⊗ ⊗ W)n=⨁ ⨁ {}i,jSilencioi+j=n}Vi⊗ ⊗ Wj{displaystyle (Votimes W)_{n}=bigoplus V_{i}otimes W_{j}

y diferencial dado por

∂ ∂ ()a⊗ ⊗ b)=∂ ∂ a⊗ ⊗ b+()− − 1)SilencioaSilencioa⊗ ⊗ ∂ ∂ b{displaystyle partial (aotimes b)=partial aotimes b+(-1)^{left sometidaaright sometida}aotimes partial b}

Donde a y b son dos vectores homogéneos en V y W respectivamente, y SilencioaSilencio{displaystyle left WordPressaright sometida} denota el grado de a.

Este producto tensorial convierte a la categoría Ch_K en una categoría monoide simétrica. El objeto de identidad respecto a este producto monoide es el anillo base K visto como una cadena compleja en grado 0. El trenzado se da sobre tensores simples de elementos homogéneos por

a⊗ ⊗ b↦ ↦ ()− − 1)SilencioaSilencioSilenciobSilenciob⊗ ⊗ a{displaystyle aotimes bmapsto (-1)^{left tuberculosisleft tolerabright sobrevivir}botimes a}

El signo es necesario para que el trenzado sea un mapa de cadenas.

Moreover, the category of chain complexes of K- también tiene nódulos internos Hom: determinados complejos de cadena V y W, el Hom interno de V y W, denotado Hom(V,W), es el complejo de cadena con grado n elementos dados por ▪ ▪ iHomK()Vi,Wi+n){displaystyle {fnMicrosoft Sans Serif} y diferenciación dada por

()∂ ∂ f)()v)=∂ ∂ ()f()v))− − ()− − 1)SilenciofSilenciof()∂ ∂ ()v)){displaystyle (partial f)(v)=partial (f(v))-(-1)^{left sometidafright sometida}f(partial (v)}.

Tenemos un isomorfismo natural

Hom()A⊗ ⊗ B,C).. Hom()A,Hom()B,C)){displaystyle {text{Hom} {otimes B,C)cong {text{Hom}}(A,{text{Hom}}(B,C)}}

Más ejemplos

• Amitsur complex
• Un complejo utilizado para definir los grupos Chow superiores de Bloch
• Complejo Buchsbaum-Rim
• Complejo de Čech
• Complejo de primos
• Complejo Eagon-Northcott
• Complejo de Gersten
• Complejo de Gráficos
• Complejo de Koszul
• Complejo de Moore
• Complejo de Schur