Código gris
| Código lucal | |||||
|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | |
| Código gris | |||||
| 4 | 3 | 2 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 0 | 1 |
| 12 | 1 | 0 | 1 | 0 | 0 |
| 13 | 1 | 0 | 1 | 1 | 1 |
| 14 | 1 | 0 | 0 | 1 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 |
El código binario reflejado (RBC), también conocido como binario reflejado (RB) o código Gray en honor a Frank Gray, es una ordenación del sistema numérico binario tal que dos valores sucesivos difieren en un solo bit (dígito binario).
Por ejemplo, la representación del valor decimal "1" en binario normalmente sería "001" y "2" sería "010". En código Gray, estos valores se representan como "001" y "011". De esa manera, incrementar un valor de 1 a 2 requiere solo un bit para cambiar, en lugar de dos.
Los códigos grises se utilizan ampliamente para evitar salidas falsas de interruptores electromecánicos y para facilitar la corrección de errores en comunicaciones digitales, como la televisión digital terrestre y algunos sistemas de televisión por cable.
Función
Muchos dispositivos indican la posición cerrando y abriendo interruptores. Si ese dispositivo usa códigos binarios naturales, las posiciones 3 y 4 están una al lado de la otra, pero los tres bits de la representación binaria difieren:
Decimal binario ... ... 3 011 4 100 ... ...
El problema con los códigos binarios naturales es que los interruptores físicos no son ideales: es muy poco probable que los interruptores físicos cambien de estado exactamente en sincronía. En la transición entre los dos estados que se muestran arriba, los tres interruptores cambian de estado. En el breve período mientras todos están cambiando, los interruptores leerán alguna posición falsa. Incluso sin keybounce, la transición podría verse como 011 — 001 — 101 — 100. Cuando los interruptores parecen estar en la posición 001, el observador no puede decir si ese es el "real" posición 1, o un estado de transición entre otras dos posiciones. Si la salida alimenta un sistema secuencial, posiblemente a través de una lógica combinacional, entonces el sistema secuencial puede almacenar un valor falso.
Este problema puede resolverse cambiando solo un interruptor a la vez, por lo que nunca hay ambigüedad de posición, lo que resulta en códigos que asignan a cada uno de un conjunto contiguo de números enteros, o a cada miembro de una lista circular, una palabra de símbolos tal que no hay dos palabras de código idénticos y cada dos palabras de código adyacentes difieren exactamente en un símbolo. Estos códigos también se conocen como unidad-distancia, single-distance, single-step, monostrophic o códigos sincopicos, en referencia a la distancia de Hamming de 1 entre códigos adyacentes.
Invención
En principio, puede haber más de un código de este tipo para una longitud de palabra dada, pero el término código Gray se aplicó por primera vez a un código binario particular para enteros no negativos, el código Gray reflejado en binario, o BRGC. Investigador de Bell Labs George R. Stibitz describió un código de este tipo en una solicitud de patente de 1941, concedida en 1943. Frank Gray introdujo el término código binario reflejado en su solicitud de patente de 1947, y señaló que el código "todavía no tenía sin nombre reconocido". Derivó el nombre del hecho de que "puede construirse a partir del código binario convencional mediante una especie de proceso de reflexión".
En la codificación estándar, el bit menos significativo sigue un patrón repetitivo de 2 encendido, 2 apagado (… 11001100 …); el siguiente dígito un patrón de 4 encendido, 4 apagado; el nésimo bit menos significativo un patrón de 2n encendido 2n apagado. La versión de cuatro bits de esto se muestra a continuación:
Decimal binario Gray Decimal
de Gray0 0000 0000 0 1 0001 0001 1 2 0010 0011 3 3 0011 0010 2 4 0100 0110 6 5 0101 0111 7 6 0110 0101 5 7 0111 0100 4 8 1000 1100 12 9 1001 1101 13 10 Graben 19, 1010 1111 15 11 1011 1110 14 12 1100 Graben 19, 1010 10 13 1101 1011 11 14 1110 1001 9 15 1111 1000 8
Para el decimal 15, el código pasa al decimal 0 con solo un cambio de interruptor. Esto se denomina propiedad cíclica o de adyacencia del código.
En las comunicaciones digitales modernas, los códigos Gray juegan un papel importante en la corrección de errores. Por ejemplo, en un esquema de modulación digital como QAM, donde los datos se transmiten típicamente en símbolos de 4 bits o más, el diagrama de constelación de la señal se organiza de modo que los patrones de bits transmitidos por los puntos de constelación adyacentes difieran solo en un bit. Al combinar esto con la corrección de errores hacia adelante capaz de corregir errores de un solo bit, es posible que un receptor corrija cualquier error de transmisión que provoque que un punto de la constelación se desvíe hacia el área de un punto adyacente. Esto hace que el sistema de transmisión sea menos susceptible al ruido.
A pesar de que Stibitz describió este código antes que Gray, el código binario reflejado recibió más tarde el nombre de Gray por otros que lo usaron. Dos solicitudes de patente diferentes de 1953 utilizan el "código Gray" como nombre alternativo para el "código binario reflejado"; uno de ellos también enumera "código de error mínimo" y "código de permutación cíclica" entre los nombres. Una solicitud de patente de 1954 hace referencia al "código Bell Telephone Gray". Otros nombres incluyen "código binario cíclico", "código de progresión cíclica", "binario de permutación cíclica" o "binario permutado cíclico" (CPB).
El código Gray a veces se atribuye erróneamente al inventor de dispositivos eléctricos del siglo XIX, Elisha Gray.
Historia y aplicación práctica
Acertijos matemáticos
Los códigos binarios reflejados se aplicaron a los acertijos matemáticos antes de que los ingenieros los conocieran.
El código Gray reflejado en binario representa el esquema subyacente del rompecabezas de anillos chino clásico, un mecanismo de rompecabezas mecánico secuencial descrito por el francés Louis Gros en 1872.
Puede servir como una guía de solución para el problema de las Torres de Hanoi, basado en un juego del francés Édouard Lucas en 1883. De manera similar, las configuraciones de juego denominadas Torres de Bucarest y Torres de Klagenfurt producen códigos Gray ternarios y pentarios..
Martin Gardner escribió un relato popular del código Gray en su columna Juegos matemáticos de agosto de 1972 en Scientific American.
El código también forma un ciclo hamiltoniano en un hipercubo, donde cada bit se ve como una dimensión.
Códigos de telegrafía
Cuando el ingeniero francés Émile Baudot dejó de usar un 6 código de unidad (6 bits) a código de 5 unidades para su sistema de telégrafo de impresión, en 1875 o 1876, ordenó los caracteres alfabéticos en su rueda de impresión usando un código binario reflejado, y asignó los códigos usando solo tres de los bits para vocales Con las vocales y consonantes ordenadas en su orden alfabético y otros símbolos colocados apropiadamente, el código de caracteres de 5 bits ha sido reconocido como un código binario reflejado. Este código se conoció como código Baudot y, con cambios menores, finalmente se adoptó como Alfabeto Telegráfico Internacional No. 1 (ITA1, CCITT-1) en 1932.
Casi al mismo tiempo, el alemán-austríaco Otto Schäffler demostró otro telégrafo de impresión en Viena usando un código binario reflejado de 5 bits para el mismo propósito, en 1874.
Conversión de señal analógica a digital
Frank Gray, que se hizo famoso por inventar el método de señalización que llegó a usarse para la televisión en color compatible, inventó un método para convertir señales analógicas en grupos de códigos binarios reflejados utilizando un aparato basado en tubos de vacío. Presentado en 1947, el método y el aparato obtuvieron una patente en 1953, y el nombre de Gray se mantuvo en los códigos. El "tubo PCM" El aparato que Gray patentó fue fabricado por Raymond W. Sears de Bell Labs, en colaboración con Gray y William M. Goodall, quienes le dieron crédito a Gray por la idea del código binario reflejado.
Gray estaba más interesado en usar los códigos para minimizar los errores en la conversión de señales analógicas a digitales; sus códigos todavía se utilizan hoy para este propósito.
Codificadores de posición
Los códigos Gray se utilizan en codificadores de posición rotatorios y lineales (codificadores absolutos y codificadores de cuadratura) con preferencia a la codificación binaria ponderada. Esto evita la posibilidad de que, cuando varios bits cambien en la representación binaria de una posición, se produzca una lectura incorrecta debido a que algunos de los bits cambian antes que otros.
Por ejemplo, algunos codificadores rotatorios proporcionan un disco que tiene un patrón de código Gray conductor de electricidad en anillos concéntricos (pistas). Cada pista tiene un contacto de resorte de metal estacionario que proporciona contacto eléctrico al patrón de código conductivo. Juntos, estos contactos producen señales de salida en forma de código Gray. Otros codificadores emplean mecanismos sin contacto basados en sensores ópticos o magnéticos para producir las señales de salida del código Gray.
Independientemente del mecanismo o la precisión de un codificador en movimiento, el error de medición de posición puede ocurrir en posiciones específicas (en los límites del código) porque el código puede estar cambiando en el momento exacto en que se lee (muestra). Un código de salida binario podría causar errores de medición de posición significativos porque es imposible hacer que todos los bits cambien exactamente al mismo tiempo. Si, en el momento de muestrear la posición, algunos bits han cambiado y otros no, la posición muestreada será incorrecta. En el caso de los codificadores absolutos, la posición indicada puede estar muy lejos de la posición real y, en el caso de los codificadores incrementales, esto puede dañar el seguimiento de la posición.
Por el contrario, el código Gray utilizado por los codificadores de posición garantiza que los códigos de dos posiciones consecutivas cualesquiera diferirán en solo un bit y, en consecuencia, solo un bit puede cambiar a la vez. En este caso, el error de posición máximo será pequeño, indicando una posición adyacente a la posición real.
Algoritmos genéticos
Debido a las propiedades de distancia de Hamming de los códigos Gray, a veces se utilizan en algoritmos genéticos. Son muy útiles en este campo, ya que las mutaciones en el código permiten cambios mayormente incrementales, pero ocasionalmente un solo cambio de bit puede causar un gran salto y dar lugar a nuevas propiedades.
Minimización de circuitos booleanos
Los códigos Gray también se utilizan para etiquetar los ejes de los mapas de Karnaugh desde 1953, así como en los gráficos circulares de Händler desde 1958, ambos métodos gráficos para la minimización de circuitos lógicos.
Corrección de errores
En las comunicaciones digitales modernas, los códigos Gray juegan un papel importante en la corrección de errores. Por ejemplo, en un esquema de modulación digital como QAM, donde los datos se transmiten típicamente en símbolos de 4 bits o más, el diagrama de constelación de la señal se organiza de modo que los patrones de bits transmitidos por los puntos de constelación adyacentes difieran solo en un bit. Al combinar esto con la corrección de errores hacia adelante capaz de corregir errores de un solo bit, es posible que un receptor corrija cualquier error de transmisión que provoque que un punto de la constelación se desvíe hacia el área de un punto adyacente. Esto hace que el sistema de transmisión sea menos susceptible al ruido.
Comunicación entre dominios de reloj
Los diseñadores de lógica digital utilizan mucho los códigos Gray para pasar información de conteo de bits múltiples entre lógica síncrona que opera a diferentes frecuencias de reloj. Se considera que la lógica opera en diferentes "dominios de reloj". Es fundamental para el diseño de chips grandes que funcionan con muchas frecuencias de reloj diferentes.
Recorrer estados en bicicleta con el mínimo esfuerzo
Si un sistema tiene que pasar por todas las combinaciones posibles de estados de encendido y apagado de algún conjunto de controles, y los cambios de los controles requieren gastos no triviales (por ejemplo, tiempo, desgaste, trabajo humano), un código Gray minimiza el número de cambios de configuración a un solo cambio para cada combinación de estados. Un ejemplo sería probar un sistema de tuberías para todas las combinaciones de ajustes de sus válvulas operadas manualmente.
Se puede construir un código Gray equilibrado, que cambia cada bit con la misma frecuencia. Dado que los cambios de bits se distribuyen uniformemente, esto es óptimo de la siguiente manera: los códigos Gray equilibrados minimizan el recuento máximo de cambios de bits para cada dígito.
Contadores de código gris y aritmética
George R. Stibitz ya utilizó un código binario reflejado en un dispositivo contador de pulsos binarios en 1941.
Un uso típico de los contadores de código Gray es crear un búfer de datos FIFO (primero en entrar, primero en salir) que tiene puertos de lectura y escritura que existen en diferentes dominios de reloj. Los contadores de entrada y salida dentro de un FIFO de puerto dual de este tipo a menudo se almacenan utilizando código Gray para evitar que se capturen estados transitorios no válidos cuando el conteo cruza los dominios del reloj. Los punteros de lectura y escritura actualizados deben pasar entre dominios de reloj cuando cambian, para poder rastrear el estado FIFO vacío y lleno en cada dominio. Cada bit de los punteros se muestrea de forma no determinista para esta transferencia de dominio de reloj. Entonces, para cada bit, se propaga el valor anterior o el valor nuevo. Por lo tanto, si más de un bit en el puntero de múltiples bits está cambiando en el punto de muestreo, un "incorrecto" el valor binario (ni nuevo ni antiguo) se puede propagar. Al garantizar que solo puede cambiar un bit, los códigos Gray garantizan que los únicos valores muestreados posibles son el valor de varios bits nuevo o antiguo. Por lo general, se utilizan códigos grises de longitud de potencia de dos.
A veces, los buses digitales en los sistemas electrónicos se utilizan para transmitir cantidades que solo pueden aumentar o disminuir de una en una, por ejemplo, la salida de un contador de eventos que se pasa entre dominios de reloj o a un convertidor de digital a analógico.. La ventaja de los códigos Gray en estas aplicaciones es que las diferencias en los retrasos de propagación de los muchos cables que representan los bits del código no pueden hacer que el valor recibido pase por estados que están fuera de la secuencia del código Gray. Esto es similar a la ventaja de los códigos Gray en la construcción de codificadores mecánicos, sin embargo, la fuente del código Gray es un contador electrónico en este caso. El contador en sí debe contar en código Gray, o si el contador funciona en binario, entonces el valor de salida del contador debe volver a sincronizarse después de que se haya convertido a código Gray, porque cuando un valor se convierte de binario a código Gray, es posible que las diferencias en los tiempos de llegada de los bits de datos binarios al circuito de conversión de binario a gris significarán que el código podría pasar brevemente por estados que están fuera de secuencia. Agregar un registro cronometrado después del circuito que convierte el valor de conteo en código Gray puede introducir un ciclo de reloj de latencia, por lo que contar directamente en código Gray puede ser ventajoso.
Para producir el siguiente valor de conteo en un contador de código Gray, es necesario tener alguna lógica combinacional que incremente el valor de conteo actual que se almacena. Una forma de incrementar un número de código Gray es convertirlo en código binario ordinario, agregarle uno con un sumador binario estándar y luego convertir el resultado nuevamente en código Gray. Otros métodos de conteo en código Gray se analizan en un informe de Robert W. Doran, incluida la toma de la salida de los primeros pestillos de los flip-flops maestro-esclavo en un contador de ondas binarias.
Direccionamiento de código gris
Como la ejecución del código del programa generalmente provoca un patrón de acceso a la memoria de instrucciones de direcciones localmente consecutivas, las codificaciones de bus que usan direccionamiento de código Gray en lugar de direccionamiento binario pueden reducir significativamente la cantidad de cambios de estado de los bits de dirección, lo que reduce el consumo de energía de la CPU. en algunos diseños de bajo consumo.
Construcción de un código Gray de n bits
La lista de código Gray reflejada en binario para n bits se puede generar recursivamente a partir de la lista para n − 1 bits reflejando la lista (es decir, enumerando las entradas al revés orden), prefijando las entradas en la lista original con un binario 0, prefijando las entradas en la lista reflejada con un binario 1 y luego concatenar la lista original con la lista invertida. Por ejemplo, generar la lista n = 3 a partir de la lista n = 2:
| 2-bit list: | 00, 01, 11, 10 | |
| Reflejado: | 10, 11, 01, 00 | |
| Entradas antiguas con prefijo 0: | 000, 001, 011, 010, | |
| Prefijo nuevas entradas con 1: | 110, 111, 101, 100 | |
| Concatenado: | 000, 001, 011, 010, | 110, 111, 101, 100 |
El código Gray de un bit es G1 = (0,1). Se puede pensar que se construyó recursivamente como se indicó anteriormente a partir de un código Gray de cero bits G0 = (Λ) que consta de una sola entrada de longitud cero. Este proceso iterativo de generar Gn+1 a partir de Gn aclara las siguientes propiedades del código estándar de reflexión:
- Gn es una permutación de los números 0,..., 2n1. (Cada número aparece exactamente una vez en la lista.)
- Gn está incrustado como la primera mitad Gn+ 1.
- Por lo tanto, la codificación es estable, en el sentido de que una vez que un número binario aparece en Gn aparece en la misma posición en todas las listas más largas; así que tiene sentido hablar de el reflectante Valor de código gris de un número: G()m) = mque refleja el código gris, contando de 0.
- Cada entrada Gn difiere sólo un poco de la entrada anterior. (La distancia Hamming es 1.)
- La última entrada Gn difiere sólo un poco de la primera entrada. (El código es cíclico.)
Estas características sugieren un método simple y rápido de traducir un valor binario en el correspondiente código Gray. Cada bit se invierte si el siguiente bit más alto del valor de entrada se establece en uno. Esto se puede realizar en paralelo por un bit-shift y operación exclusiva si están disponibles: el nel código gris se obtiene por computación . Prependiendo de 0 bit deja el orden de las palabras clave sin cambios, prependiendo de un 1 bit revierte el orden de las palabras clave. Si los bits en posición de las palabras clave son invertidos, el orden de bloques vecinos Las palabras clave se revierten. Por ejemplo, si el bit 0 se invierte en una secuencia de palabras clave de 3 bits, el orden de dos palabras clave vecinas se invierte
- 000,001,010,011,100,101,110,111 → 001,000,011,010,101,100,111,110 (invert bit 0)
Si se invierte el bit 1, los bloques de 2 palabras clave cambian de orden:
- 000,001,010,011,100,101,110,111 → 010,011,000,001,110,111,100,101 (invertir bit 1)
Si se invierte el bit 2, los bloques de 4 palabras de código se invierten:
- 000,001,010,011,100,101,110,111 → 100,101,110,111,000,001,010,011 (invert bit 2)
Por lo tanto, realizar una exclusiva o un poco en posición con el bit en posición deja el orden de las palabras clave intactas si , y revierte el orden de bloques codewords si . Ahora, esta es exactamente la misma operación que el método reflect-and-prefix para generar el código Gray.
Un método similar se puede utilizar para realizar la traducción inversa, pero la computación de cada bit depende del valor calculado de la próxima parte superior, por lo que no se puede realizar en paralelo. Sumas es un poco codificado por Gray ( ser el bit más importante), y es t bit de código binario ( siendo el bit más significativo), la traducción inversa se puede dar recursivamente: , y . Alternativamente, decodificar un código gris en un número binario se puede describir como una suma prefijo de los bits en el código gris, donde cada operación de summación individual en la suma prefijo se realiza modulo dos.
Para construir el reflejo binario Código gris iterativamente, a paso 0 comienza con el , y a paso encontrar la posición de bit del menos significativo 1 en la representación binaria de y voltear el bit en esa posición en el código anterior para obtener el siguiente código . Las posiciones del bit comienzan 0, 1, 0, 2, 0, 1, 0, 3,... Vea el primer set para algoritmos eficientes para calcular estos valores.
Conversión ay desde código Gray
Las siguientes funciones en C convierten entre números binarios y sus códigos Gray asociados. Si bien puede parecer que la conversión de Gray a binario requiere que cada bit se maneje uno a la vez, existen algoritmos más rápidos.
Tipodef no firmado int Uint;// Esta función convierte un número binario no firmado para reflejar código binario Gray.Uint BinaryToGray()Uint num){} retorno num ^ ()num > 1); // La operadora √Īo está cambiando a la derecha. El operador ^ es exclusivo o.}// Esta función convierte un número de código binario Gray en un número binario.Uint GrayToBinary()Uint num){} Uint máscara = num; mientras ()máscara) {} // Cada uno El bit de código gris es exclusivo con todos los bits más significativos. máscara > 1; num ^= máscara; } retorno num;}// Una versión más eficiente para códigos grises 32 bits o menos a través del uso de técnicas SWAR (SIMD dentro de un registro). // Implementa una función paralela de prefijo XOR. Las declaraciones de asignación pueden estar en cualquier orden.// // Esta función se puede adaptar para códigos grises más largos añadiendo pasos.Uint GrayToBinary32()Uint num){} num ^= num > 16; num ^= num > 8; num ^= num > 4; num ^= num > 2; num ^= num > 1; retorno num;}// Una variante de cuatro bits a cero cambia un número binario (abcd)2 a (abcd)2 ^ (00ab)2, luego a (abcd)2 ^ (00ab)2 ^ (0abc)2 ^ (000a)2.En los procesadores más nuevos, la cantidad de instrucciones ALU en el paso de decodificación se puede reducir aprovechando el conjunto de instrucciones CLMUL. Si MASK es la cadena binaria constante de unos terminada con un solo dígito cero, entonces la multiplicación sin acarreo de MASK con la codificación gris de x siempre dará x o su negación bit a bit.
Tipos especiales de códigos Gray
En la práctica, el "código Gray" casi siempre se refiere a un código Gray reflejado binario (BRGC). Sin embargo, los matemáticos han descubierto otros tipos de códigos Gray. Al igual que los BRGC, cada uno consiste en una lista de palabras, donde cada palabra difiere de la siguiente en solo un dígito (cada palabra tiene una distancia de Hamming de 1 desde la siguiente palabra).
Códigos grises de n bits y de longitud inferior a 2n
Es posible construir códigos Gray binarios con n bits con una longitud inferior a 2n , si la longitud es uniforme. Una posibilidad es comenzar con un código Gray equilibrado y eliminar pares de valores al principio y al final, o en el medio. La secuencia OEIS A290772 da el número de posibles secuencias grises de longitud 2 n que incluyen cero y utilizan el número mínimo de bits.
Código Gray N-ario
|
Hay muchos tipos especializados de códigos Gray además del código Gray reflejado en binario. Uno de estos tipos de código Gray es el código n-ary Gray, también conocido como código Gray no booleano. Como su nombre lo indica, este tipo de código Gray utiliza valores no booleanos en sus codificaciones.
Por ejemplo, un código Gray 3-ario (ternario) usaría los valores 0,1,2. El (n, k)-código Gray es el código n-ario Gray con k< /i> dígitos. La secuencia de elementos en el código (3, 2)-Gray es: 00,01,02,12,11,10,20,21,22. El código (n, k)-Gray se puede construir de forma recursiva, como el BRGC, o se puede construir de forma iterativa. Se presenta un algoritmo para generar iterativamente el código (N, k)-Gray (en C):
// entradas: base, dígitos, valor// salida: Gray// Convertir un valor en un código gris con la base y los dígitos dados.// La iteración a través de una secuencia de valores resultaría en una secuencia// de códigos grises en los que sólo un dígito cambia a la vez.vacío toGray()no firmado base, no firmado dígitos, no firmado valor, no firmado gris[dígitos]){} no firmado baseN[dígitos];// Almacena el número base-N ordinario, un dígito por entradano firmado i;// La variable de bucle // Ponga el número baseN normal en el array baseN. Para la base 10, 109 // se almacenaría como [9,0,1]para ()i = 0; i . dígitos; i++) {}baseN[i] = valor % base;valor = valor / base;} // Convertir el número baseN normal en el equivalente código gris. Note que// el bucle comienza en el dígito más significativo y baja.no firmado cambio = 0;mientras ()i--) {}// El dígito gris se cambia por la suma de lo más alto// dígitos.gris[i] = ()baseN[i] + cambio) % base;cambio = cambio + base - gris[i];// Subtract from base so shift is positive}}// EXAMPLES// entrada: valor = 1899, base = 10, dígitos = 4// output: baseN[] = [9,8,1], gray[] = [0,1,7,1]// entrada: valor = 1900, base = 10, dígitos = 4// output: baseN[] = [0,0,9,1], gray[] = [0,1,8,1]Hay otros algoritmos de código Gray para (n,k)-códigos Gray. El código (n,k)-Gray producido por el algoritmo anterior siempre es cíclico; algunos algoritmos, como el de Guan, carecen de esta propiedad cuando k es impar. Por otro lado, aunque con este método solo cambia un dígito a la vez, puede cambiar ajustando (recorriendo de n − 1 a 0). En el algoritmo de Guan, el conteo sube y baja alternativamente, de modo que la diferencia numérica entre dos dígitos del código Gray es siempre uno.
Los códigos Gray no están definidos de forma única, porque una permutación de las columnas de dicho código también es un código Gray. El procedimiento anterior produce un código en el que cuanto menor es el significado de un dígito, más a menudo cambia, lo que lo hace similar a los métodos de conteo normales.
Consulte también el sistema numérico binario sesgado, una variante del sistema numérico ternario en el que, como máximo, dos dígitos cambian en cada incremento, ya que cada incremento se puede realizar con una operación de acarreo de un dígito como máximo.
Código gris equilibrado
Aunque el código binario reflejado de Gray es útil en muchos escenarios, no es óptimo en ciertos casos debido a la falta de "uniformidad". In códigos Gray equilibrados, el número de cambios en diferentes posiciones de coordinación son lo más cerca posible. Para hacer esto más preciso, deja G ser un R- Completa Ciclo gris con secuencia de transición ; el conteos de transición ()espectro espectro espectro espectro espectro espectro espectro espectro espectro espectro espectro espectro espectro espectro) de G son la colección de enteros definidos por
Un código gris es uniforme o uniformemente equilibrado si sus cuentas de transición son iguales, en cuyo caso tenemos para todos k. Claramente, cuando , tales códigos existen solamente si n es un poder de 2. Si n no es un poder de 2, es posible construir equilibrado códigos binarios donde la diferencia entre dos conteos de transición es a la mayoría de 2; por lo que (combinando ambos casos) cada conteo de transición es o bien o . Los códigos grises también pueden ser exponencialmente equilibrada si todos sus conteos de transición son poderes adyacentes de dos, y tales códigos existen para cada poder de dos.
Por ejemplo, un código Gray equilibrado de 4 bits tiene 16 transiciones, que se pueden distribuir uniformemente entre las cuatro posiciones (cuatro transiciones por posición), lo que lo hace uniformemente equilibrado:
- 0 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0
- 0 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0
- 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 0 0
- 0 0 1 1 0 0 0 0 1 1 1 1 1 1 1
mientras que un código Gray equilibrado de 5 bits tiene un total de 32 transiciones, que no se pueden distribuir uniformemente entre las posiciones. En este ejemplo, cuatro posiciones tienen seis transiciones cada una y una tiene ocho:
- 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0
- 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 1 1 0 0
- 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1
- 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 1
- 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 1 1 1 1
Ahora mostraremos una construcción e implementación para códigos binarios bien balanceados que nos permiten generar un n-Digit balanceado Código gris para todos n. El principio principal es construir inductivamente un (n+ 2)-digit Código gris dado n-digit Código Gray G de tal manera que se conserva la propiedad equilibrada. Para ello, consideramos particiones de en un número incluso L de bloques no vacíos de la forma
Donde , , y ). Esta partición induce a -digit Código Gray dado por
Si definimos las multiplicidades de transición
para ser el número de veces el dígito en posición i cambios entre bloques consecutivos en una partición, entonces para el (n+ 2)-digit Código gris inducido por esta partición el espectro de transición es
La parte delicada de esta construcción es encontrar una partición adecuada de un equilibrio n-digit Código gris de tal manera que el código inducido por él permanece equilibrado, pero por esto sólo las multiplicidades de transición importan; uniendo dos bloques consecutivos sobre un dígito transición y dividir otro bloque en otro dígito transición produce un código gris diferente con exactamente el mismo espectro de transición , por lo que uno puede por ejemplo designar el primero transiciones a dígitos como los que caen entre dos bloques. Los códigos uniformes se pueden encontrar cuando y , y esta construcción se puede extender a la R- El caso también.
Códigos grises de larga duración
Longitud (o brecha máxima) Los códigos grises maximizan la distancia entre cambios consecutivos de dígitos en la misma posición. Es decir, la longitud de ejecución mínima de cualquier bit permanece sin cambios durante el mayor tiempo posible.
Códigos grises monotónicos
Los códigos monotónicos son útiles en la teoría de las redes de interconexión, especialmente para minimizar la dilatación de las matrices lineales de procesadores. Si definimos el peso de una cadena binaria como el número de 1 en la cadena, entonces aunque claramente no podemos tener un código Gray con un peso estrictamente creciente, es posible que queramos aproximarnos a esto teniendo el código pasar por dos pesas adyacentes antes de llegar a la siguiente.
Podemos formalizar el concepto de códigos monotone Gray como sigue: considerar la partición del hipercubo en niveles de vértices que tienen igual peso, es decir.
para . Estos niveles satisfacen . Vamos ser el subgrafo de inducido por , y dejar ser los bordes en . Un código gris monotónico es entonces un camino Hamiltoniano en tal como sea viene antes en el camino, entonces .
Una elegante construcción de monotónico n-digit Códigos Gray para cualquier n se basa en la idea de subpaths de construcción recurrente de longitud tener bordes en . Definimos , siempre o , y
De lo contrario. Aquí, es una permutación adecuada y se refiere al camino P con sus coordenadas permutadas por . Estos caminos dan lugar a dos monotónicos n-digit Códigos Gray y dado por
La elección de que asegura que estos códigos son de hecho códigos grises resulta ser . Los primeros valores de se muestran en la tabla siguiente.
| j = 0 | j = 1 | j = 2 | j = 3 | |
|---|---|---|---|---|
| n = 1 | 0, 1 | |||
| n = 2 | 00, 01 | 10, 11 | ||
| n = 3 | 000, 001 | 100, 110, 010, 011 | 101, 111 | |
| n = 4 | 0000, 0001 | 1000, 1100, 0100, 0110, 0010, 0011 | 1010, 1011, 1001, 1101, 0101, 0111 | 1110, 1111 |
Estos códigos Gray monotónicos se pueden implementar de manera eficiente de tal manera que cada elemento subsiguiente se pueda generar en tiempo O(n). El algoritmo se describe más fácilmente usando corrutinas.
Los códigos monotónicos tienen una conexión interesante con la conjetura de Lovász, que afirma que cada gráfico conectado con el vertex-transitivo contiene un camino Hamiltoniano. El subgrafo de nivel medio es vértice-transitivo (es decir, su grupo de automorfismo es transitivo, de modo que cada vértice tiene el mismo "ambiente local" y no puede diferenciarse de los otros, ya que podemos reetiquetar las coordenadas así como los dígitos binarios para obtener un automorfismo) y el problema de encontrar un camino Hamiltoniano en este subgrafo se llama el "problema de niveles medio", que puede proporcionar información sobre el conje más general. La pregunta ha sido respondida afirmativamente , y la construcción anterior para códigos monotónicos garantiza un camino de longitud Hamiltoniano al menos 0.839N Donde N es el número de vértices en el subgrafo de nivel medio.
Código Beckett-Gray
Otro tipo de código Gray, el código Beckett-Gray, lleva el nombre del dramaturgo irlandés Samuel Beckett, que estaba interesado en la simetría. Su obra "Quad" cuenta con cuatro actores y se divide en dieciséis períodos de tiempo. Cada período termina con uno de los cuatro actores entrando o saliendo del escenario. La obra comienza y termina con un escenario vacío, y Beckett quería que cada subconjunto de actores apareciera en el escenario exactamente una vez. Claramente, el conjunto de actores actualmente en el escenario puede representarse mediante un código Gray binario de 4 bits. Beckett, sin embargo, colocó una restricción adicional en el guión: deseaba que los actores entraran y salieran para que el actor que había estado más tiempo en el escenario fuera siempre el que saliera. Los actores podrían entonces ser representados por una cola de primero en entrar, primero en salir, de modo que (de los actores en el escenario) el actor que está siendo sacado de la cola es siempre el que fue puesto primero en la cola. Beckett no pudo encontrar un código Beckett-Gray para su obra y, de hecho, una lista exhaustiva de todas las secuencias posibles revela que no existe tal código para n = 4. Hoy se sabe que tales códigos no existen para n = 2, 5, 6, 7 y 8, y no existen para n = 3 o 4. Un ejemplo de Beckett–Gray de 8 bits El código se puede encontrar en El arte de la programación de computadoras de Donald Knuth. Según Sawada y Wong, el espacio de búsqueda para n = 6 se puede explorar en 15 horas y se han encontrado más de 9.500 soluciones para el caso n = 7.
Códigos de serpiente en la caja
Los códigos de serpiente en la caja, o serpientes, son las secuencias de nodos de caminos inducidos en un gráfico de hipercubo n-dimensional, y la bobina en- los códigos de caja, o bobinas, son las secuencias de nodos de ciclos inducidos en un hipercubo. Vistas como códigos Gray, estas secuencias tienen la propiedad de poder detectar cualquier error de codificación de un solo bit. Los códigos de este tipo fueron descritos por primera vez por William H. Kautz a fines de la década de 1950; desde entonces, se ha investigado mucho para encontrar el código con el mayor número posible de palabras clave para una dimensión de hipercubo determinada.
Código Gray de vía única
Otro tipo de código Gray es el código Gray de vía única (STGC) desarrollado por Norman B. Spedding y refinado por Hiltgen, Paterson y Brandestini en "Códigos grises de vía única& #34; (1996). El STGC es una lista cíclica de codificaciones binarias únicas P de longitud n tales que dos palabras consecutivas difieren exactamente en una posición, y cuando la lista se examina como P × < matriz i>n, cada columna es un desplazamiento cíclico de la primera columna.
El nombre proviene de su uso con codificadores rotatorios, donde los contactos detectan una cantidad de pistas, lo que da como resultado para cada una una salida de 0 o 1. Para reducir el ruido debido a que diferentes contactos no cambian exactamente en el mismo momento, es preferible configurar las pistas para que la salida de datos de los contactos esté en código Gray. Para obtener una alta precisión angular, se necesitan muchos contactos; para lograr al menos 1° de precisión, se necesitan al menos 360 posiciones distintas por revolución, lo que requiere un mínimo de 9 bits de datos y, por lo tanto, el mismo número de contactos.
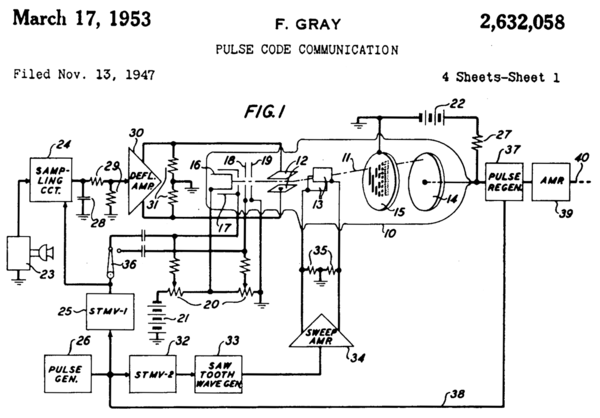
Si todos los contactos se colocan en la misma posición angular, se necesitan 9 pistas para obtener un BRGC estándar con al menos 1° de precisión. Sin embargo, si el fabricante mueve un contacto a una posición angular diferente (pero a la misma distancia del eje central), entonces el "patrón de anillo" necesita ser girado el mismo ángulo para dar la misma salida. Si el bit más significativo (el anillo interior en la Figura 1) se gira lo suficiente, coincide exactamente con el siguiente anillo. Dado que ambos anillos son idénticos, el anillo interior se puede cortar y el sensor de ese anillo se mueve al anillo idéntico restante (pero desplazado en ese ángulo desde el otro sensor en ese anillo). Esos dos sensores en un solo anillo hacen un codificador de cuadratura. Eso reduce el número de pistas para una resolución de "1°" Codificador angular de 8 pistas. No se puede reducir aún más el número de pistas con BRGC.
Durante muchos años, Torsten Sillke y otros matemáticos creyeron que era imposible codificar la posición en una sola pista de modo que las posiciones consecutivas difirieran en un solo sensor, excepto en el codificador de cuadratura de 1 pista y 2 sensores. Entonces, para aplicaciones en las que 8 pistas eran demasiado voluminosas, la gente usaba codificadores incrementales de una sola pista (codificadores de cuadratura) o "codificador de cuadratura + muesca de referencia" de 2 pistas. codificadores
Sin embargo, Norman B. Spedding registró una patente en 1994 con varios ejemplos que demuestran que era posible. Aunque no es posible distinguir 2 posiciones n con sensores n en una sola pista, es posible distinguir cerca de tantos. Etzion y Paterson conjeturan que cuando n es en sí mismo una potencia de 2, los sensores n pueden distinguir como máximo 2n − 2n posiciones y que para primos n el límite es de 2n − 2 posiciones. Los autores continuaron generando un código de pista única de 504 posiciones de longitud 9 que creen que es óptimo. Dado que este número es mayor que 28 = 256, cualquier código requiere más de 8 sensores, aunque un BRGC podría distinguir 512 posiciones con 9 sensores.
Aquí se reproduce un STGC para P = 30 y n = 5:
Código Gray de una sola pista para 30 posiciones Angle Código Angle Código Angle Código Angle Código Angle Código 0° 10000 72° 01000 144° 00100 216° 00010 288° 00001 12° 10100 84° 01010 156° 00101 228° 10010 300° 01001 24° 11100 96° 01110 168° 00111 240° 10011 312° 11001 36° 11110 108° 01111 180° 10111 252° 11011 324° 11101 48° 11010 120° 01101 192° 10110 264° 01011 336° 10101 60° 11000 132° 01100 204° 00110 276° 00011 348° 10001
Cada columna es un cambio cíclico de la primera columna, y de cualquier fila a la fila siguiente solo cambia un bit. La naturaleza de una sola pista (como una cadena de código) es útil en la fabricación de estas ruedas (en comparación con BRGC), ya que solo se necesita una pista, lo que reduce su costo y tamaño. La naturaleza del código Gray es útil (en comparación con los códigos de cadena, también llamados secuencias de De Bruijn), ya que solo un sensor cambiará en cualquier momento, por lo que la incertidumbre durante una transición entre dos estados discretos será solo más o menos una unidad de angular. medición que el dispositivo es capaz de resolver.
Código Gray bidimensional
Los códigos Gray bidimensionales se utilizan en la comunicación para minimizar la cantidad de errores de bit en los puntos adyacentes de la modulación de amplitud en cuadratura (QAM) en la constelación. En una codificación típica, los puntos de constelación adyacentes horizontales y verticales difieren en un solo bit, y los puntos adyacentes diagonales difieren en 2 bits.
Los códigos Gray bidimensionales también tienen usos en los esquemas de identificación de ubicaciones, donde el código se aplicaría a mapas de área como una proyección de Mercator de la superficie terrestre y una función de distancia bidimensional cíclica apropiada como la La métrica de Mannheim se puede utilizar para calcular la distancia entre dos ubicaciones codificadas, combinando así las características de la distancia de Hamming con la continuación cíclica de una proyección de Mercator.
Exceso-Código-Gray
Si se extrae una subsección de un valor de código específico a partir de ese valor, por ejemplo, los últimos 3 bits de un código gris de 4 bits, el código resultante será un "código gris en exceso". Este código muestra la propiedad de contar hacia atrás en esos bits extraídos si el valor original se incrementa aún más. La razón de esto es que los valores codificados en gris no muestran el comportamiento de desbordamiento, conocido por la codificación binaria clásica, cuando aumentan más allá del "más alto" valor.
Ejemplo: el código gris de 3 bits más alto, 7, se codifica como (0)100. Agregar 1 da como resultado el número 8, codificado en gris como 1100. Los últimos 3 bits no se desbordan y cuentan hacia atrás si aumenta aún más el código original de 4 bits.
Cuando se trabaja con sensores que emiten múltiples valores codificados en gris de forma serial, se debe prestar atención a si el sensor genera esos valores múltiples codificados en un solo código gris o como valores separados, ya que de lo contrario los valores podrían aparecer estar contando hacia atrás cuando un "desbordamiento" se espera.
Isometría gris
El mapeo bijetivo { 0 ↔ 00, 1 ↔ 01, 2 ↔ 11, 3 ↔ 10 } establece una isometría entre el espacio métrico sobre el campo finito con la métrica dada por la distancia Hamming y el espacio métrico sobre el anillo finito (la aritmética modular habitual) con la métrica dada por la distancia Lee. El mapeo se extiende adecuadamente a una isometría de los espacios de Hamming y . Su importancia radica en establecer una correspondencia entre varios códigos "buenos" pero no necesariamente lineales como imágenes de mapas grises en de códigos lineales de anillo .
Códigos relacionados
Hay una serie de códigos binarios similares a los códigos Gray, que incluyen:
- Datex codes aka Giannini codes (1954), como lo describe Carl P. Spaulding, usa una variante del código O'Brien II.
- Los códigos utilizados por Varec (ca. 1954), utilizan una variante del código I de O'Brien, así como las variantes de código base-12 y base-16 Gray.
- Código lucal (1959) aka modificado reflejado código binario (MRB)
- El código Gillham (1961/1962), utiliza una variante del código Datex y el código O'Brien II.
- Leslie y Russell código (1964)
- Código de Establecimiento de Radar Real
- Código Hoklas (1988)
Los siguientes códigos decimales codificados en binario (BCD) también son variantes del código Gray:
- Código Petherick (1953), también conocido como Código Royal Aircraft Establishment (RAE).
- Códigos O'Brien I y II (1955) (Un código O'Brien tipo I ya fue descrito por Frederic A. Foss de IBM y utilizado por Varec en 1954. Más tarde, también fue conocido como código Watts o Watts reflejado el código decimal (WRD) y a veces se conoce ambiguamente como código de gris modificado binario reflejado. Un código O'Brien tipo-II ya fue utilizado por Datex en 1954.)
- Exceso-3 Código gris (1956) (también código Gray exceso-3, código gris 3-exceso, exceso de reflejo 3 código, exceso de Código gris, código de exceso gris, código gris de 10-excesos-3 o código gris-Stibitz), descrito por Frank P. Turvey Jr. de ITT.
- Tompkins codes I and II (1956)
- Código Glixon (1957), a veces ambiguamente también llamado código gris modificado
| Nombre | Bit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Pesos | Pistas | Compl. | Cyclic | 5s | Comentario |
| Gray BCD | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 a 3 | 4 3) | No | (2, 4, 8, 16) | No | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Paul | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 a 3 | 4 3) | No | 2, 10 | No | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |||||||
| Glixon | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 a 3 | 4 | No | 2, 4, 8, 10 | (shifted +1) | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |||||||
| Tompkins I | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0-4 | 2 | No | 2, 4, 10 | Sí. | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
| O'Brien I (Wats) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 a 3 | 4 | 9 | 2, 4, 10 | Sí. | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |||||||
| Petherick (RAE) | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 a 3 | 3 | 9 | 2, 10 | Sí. | |
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| O'Brien II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 a 3 | 3 | 9 | 2, 10 | Sí. | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| Susskind | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1-4 | 3 | 9 | 2, 10 | Sí. | |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| Klar | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0-4 | 4 3) | 9 | 2, 10 | Sí. | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Tompkins II | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 a 3 | 2 | 9 | 2, 10 | Sí. | |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | |||||||
| Exceso-3 Gray | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1-4 | 4 | 9 | 2, 10 | Sí. | |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |||||||
Contenido relacionado
Jose whitworth
GNU Hurd
Heckler & koch