Código convolucional

En telecomunicaciones, un código convolucional es un tipo de código de corrección de errores que genera símbolos de paridad mediante la aplicación deslizante de una función polinomial booleana a un flujo de datos. La aplicación deslizante representa la 'convolución' del codificador sobre los datos, lo que da lugar al término 'codificación convolucional'. La naturaleza deslizante de los códigos convolucionales facilita la decodificación de Trellis utilizando un Trellis invariable en el tiempo. La decodificación Trellis invariable en el tiempo permite que los códigos convolucionales se decodifiquen con una decisión suave de máxima probabilidad con una complejidad razonable.

La capacidad de realizar la decodificación de decisiones suaves de máxima probabilidad económica es uno de los principales beneficios de los códigos conversos. Esto contrasta con los códigos de bloques clásicos, que generalmente están representados por un trellis de tiempo y por lo tanto son típicamente descodificados por decisión dura. Los códigos convolutivos se caracterizan a menudo por la tasa de código base y la profundidad (o memoria) del encoder [n,k,K]{displaystyle [n,k,K]}. La tasa de código base se suele dar como n/k{displaystyle No., donde n es la tasa de datos de entrada cruda k es la tasa de datos del canal de salida de flujo codificado. n es menos que k porque la codificación del canal inserta redundancia en los bits de entrada. La memoria se llama a menudo la "longitud del tren" K, donde la salida es una función de la entrada actual, así como la anterior K− − 1{displaystyle K-1 entradas. La profundidad también se puede dar como el número de elementos de memoria v en el polinomio o el número máximo posible de estados del encoder (típicamente: 2v{displaystyle 2^{v}).

Los códigos convolucionales a menudo se describen como continuos. Sin embargo, también se puede decir que los códigos convolucionales tienen una longitud de bloque arbitraria, en lugar de ser continuos, ya que la mayor parte de la codificación convolucional del mundo real se realiza en bloques de datos. Los códigos de bloque codificados convolucionalmente emplean típicamente terminación. La longitud de bloque arbitraria de los códigos convolucionales también se puede contrastar con los códigos de bloque clásicos, que generalmente tienen longitudes de bloque fijas determinadas por propiedades algebraicas.

La tasa de código de un código convocional se modifica comúnmente a través de puntuación de símbolos. Por ejemplo, un código converso con una tasa de código 'madre' n/k=1/2{displaystyle n/k=1/2} puede ser perforado a una tasa más alta, por ejemplo, 7/8{displaystyle 7/8} simplemente por no transmitir una porción de símbolos de código. El rendimiento de un código converso perforado generalmente escala bien con la cantidad de paridad transmitida. La capacidad de realizar la decodificación económica de decisiones suaves sobre códigos conversos, así como la longitud de bloque y la flexibilidad de la tasa de código de códigos convolutivos, los hace muy populares para las comunicaciones digitales.

Historia

Los códigos convolucionales fueron introducidos en 1955 por Peter Elias. Se pensó que los códigos convolucionales podrían decodificarse con calidad arbitraria a expensas del cálculo y la demora. En 1967, Andrew Viterbi determinó que los códigos convolucionales podían decodificarse con máxima probabilidad y con una complejidad razonable utilizando decodificadores basados en trellis invariantes en el tiempo: el algoritmo de Viterbi. Posteriormente se desarrollaron otros algoritmos decodificadores basados en trellis, incluido el algoritmo de decodificación BCJR.

Los códigos convolucionales sistemáticos recursivos fueron inventados por Claude Berrou alrededor de 1991. Estos códigos demostraron ser especialmente útiles para el procesamiento iterativo, incluido el procesamiento de códigos concatenados, como los códigos turbo.

Usando el "convolucional" terminología, un código convolucional clásico podría considerarse un filtro de respuesta de impulso finito (FIR), mientras que un código convolucional recursivo podría considerarse un filtro de respuesta de impulso infinito (IIR).

Donde se utilizan códigos convolucionales

Estadios de codificación de canales en GSM. Codificación de bloques y verificación de paridad - parte de detección de errores. Convolutional encoder and Viterbi decoder - error de corrección parte. Interleaving and Deinterleaving - la separación de palabras de código aumenta en el dominio del tiempo y para evitar distorsiones irrumpidas.

Los códigos convolucionales se usan ampliamente para lograr una transferencia de datos confiable en numerosas aplicaciones, como video digital, radio, comunicaciones móviles (por ejemplo, en redes GSM, GPRS, EDGE y 3G (hasta la versión 7 de 3GPP)) y comunicaciones por satélite. Estos códigos a menudo se implementan en concatenación con un código de decisión difícil, particularmente Reed-Solomon. Antes de los códigos turbo, tales construcciones eran las más eficientes y se acercaban más al límite de Shannon.

Codificación convolucional

Para codificar datos de forma convolucional, comience con registros de memoria k, cada uno con un bit de entrada. A menos que se especifique lo contrario, todos los registros de memoria comienzan con un valor de 0. El codificador tiene n sumadores de módulo 2 (un sumador de módulo 2 se puede implementar con una sola puerta booleana XOR, donde la lógica es: 0+0 = 0, 0+1 = 1, 1+0 = 1, 1+1 = 0), y n polinomios generadores: uno para cada sumador (consulte la figura a continuación). Un bit de entrada m₁ se introduce en el registro más a la izquierda. Usando los polinomios generadores y los valores existentes en los registros restantes, el codificador genera n símbolos. Estos símbolos pueden transmitirse o perforarse dependiendo de la tasa de código deseada. Ahora cambie los bits de todos los valores de registro a la derecha (m₁ se mueve a m₀, m₀ se mueve a m₋₁) y espera el siguiente bit de entrada. Si no quedan bits de entrada, el codificador continúa desplazándose hasta que todos los registros hayan vuelto al estado cero (terminación de bits de descarga).

Img.1. Tasa 1/3 encoder no recursivo y no sistemático con la longitud de restricción 3

La siguiente figura es una tasa 1⁄3 (m⁄n ) con longitud de restricción (k) de 3. Los polinomios generadores son G₁ = (1,1,1), G₂ = (0,1, 1), y G₃ = (1,0,1). Por lo tanto, los bits de salida se calculan (módulo 2) de la siguiente manera:

n₁ = m₁ + m₀ + m₋₁

n₂ = m₀ + m₋₁

n₃ = m₁ + m₋₁.

Los códigos convolucionales pueden ser sistemáticos y no sistemáticos:

• sistemática repite la estructura del mensaje antes de la codificación
• cambios no sistemáticos de la estructura inicial

Los códigos convolucionales no sistemáticos son más populares debido a una mejor inmunidad al ruido. Se relaciona con la distancia libre del código convolucional.

• 

  Una breve ilustración del código converso no sistemático.

• 

  Una breve ilustración del código convocional sistemático.

Códigos recursivos y no recursivos

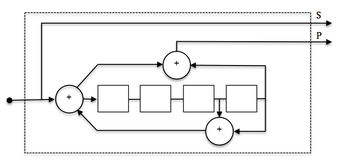
El codificador de la imagen de arriba es un codificador no recursivo. Aquí hay un ejemplo de uno recursivo y, como tal, admite una estructura de retroalimentación:

Img.2. Tasa 1/2 Codificador convolutivo sistemático de 8 estados. Utilizado como código constitutivo en 3GPP 25.212 Turbo Code.

El codificador de ejemplo es sistemático porque los datos de entrada también se utilizan en los símbolos de salida (Salida 2). Los códigos con símbolos de salida que no incluyen los datos de entrada se denominan no sistemáticos.

Los códigos recursivos suelen ser sistemáticos y, por el contrario, los códigos no recursivos suelen ser no sistemáticos. No es un requisito estricto, sino una práctica común.

El codificador de ejemplo en Img. 2. es un codificador de 8 estados porque los 3 registros crearán 8 posibles estados de codificador (2³). Un enrejado de decodificador correspondiente normalmente también usará 8 estados.

Los códigos convolucionales sistemáticos recursivos (RSC) se han vuelto más populares debido a su uso en Turbo Codes. Los códigos sistemáticos recursivos también se denominan códigos pseudosistemáticos.

Otros códigos RSC y aplicaciones de ejemplo incluyen:

Img. 3. Código contrarrevolucionario sistemático de dos estados (RSC). También se llama 'acumulador. '

Útil para la implementación de código LDPC y como código constituyente interno para códigos convolucionales concatenados en serie (SCCC's).

Img. 4. Código convolutivo sistemático de cuatro estados (RSC).

Útil para SCCC's y códigos turbo multidimensionales.

Img. 5. Código conversor sistemático de 16 estados (RSC).

Útil como código constituyente en códigos turbo de baja tasa de error para aplicaciones como enlaces satelitales. También adecuado como código exterior SCCC.

Respuesta de impulso, función de transferencia y longitud de restricción

Un codificador convolucional se llama así porque realiza una convolución del flujo de entrada con las respuestas de impulso del codificador:

Sí.ij=.. k=0JUEGO JUEGO hkjxi− − k=()xAlternativa Alternativa hj)[i],{displaystyle Y... ¿Qué? [i],}

Donde x es una secuencia de entrada, Sí.^j es una secuencia de salida j, h^j es una respuesta de impulso para la salida j y Alternativa Alternativa {displaystyle {}} denota la revolución.

Un codificador convolucional es un sistema discreto lineal invariable en el tiempo. Cada salida de un codificador se puede describir mediante su propia función de transferencia, que está estrechamente relacionada con el polinomio generador. Una respuesta de impulso está conectada con una función de transferencia a través de la transformada Z.

Las funciones de transferencia para el primer codificador (no recursivo) son:

• H1()z)=1+z− − 1+z− − 2,{displaystyle H_{1}(z)=1+z^{-1}+z^{-2},, }
• H2()z)=z− − 1+z− − 2,{displaystyle H_{2}(z)=z^{-1}+z^{-2},}
• H3()z)=1+z− − 2.{displaystyle H_{3}(z)=1+z^{-2}

Las funciones de transferencia para el segundo codificador (recursivo) son:

• H1()z)=1+z− − 1+z− − 31− − z− − 2− − z− − 3,{displaystyle H_{1}(z)={frac {1+z^{-1}+z^{-3}{1-z^{-2}-z^{-3}},}
• H2()z)=1.{displaystyle H_{2}(z)=1.,}

Definir m por

m=maxipolideg⁡ ⁡ ()Hi()1/z)){displaystyle m=max _{i}operatorname {polydeg} (H_{i}(1/z),}

donde, para cualquier función racional f()z)=P()z)/Q()z){displaystyle f(z)=P(z)/Q(z),},

polideg⁡ ⁡ ()f)=max()deg⁡ ⁡ ()P),deg⁡ ⁡ ()Q)){displaystyle operatorname {polydeg} (f)=max(deg(P),deg(Q)),}.

Entonces... m es el máximo de los grados polinomios del Hi()1/z){displaystyle H_{i}(1/z),}, y el limitación de la longitud se define como K=m+1{displaystyle K=m+1,}. Por ejemplo, en el primer ejemplo la longitud de restricción es 3, y en el segundo la longitud de restricción es 4.

Diagrama Trellis

Un codificador convolucional es una máquina de estados finitos. Un codificador con n celdas binarias tendrá 2 estados ⁿ.

Imagine que el codificador (que se muestra en Img.1, arriba) tiene '1' en la celda de memoria izquierda (m₀), y '0' en el de la derecha (m₋₁). (m₁ no es realmente una celda de memoria porque representa un valor actual). Designaremos tal estado como "10". De acuerdo con un bit de entrada, el codificador en el siguiente giro puede convertir al "01" estado o el "11" Expresar. Se puede ver que no todas las transiciones son posibles (por ejemplo, un decodificador no puede convertir del estado "10" al "00" o incluso permanecer en "10&# 34; estado).

Todas las transiciones posibles se pueden mostrar a continuación:

Img.6. Un diagrama de trellis para el encoder en Img.1. Un camino a través de los trellis se muestra como una línea roja. Las líneas sólidas indican las transiciones donde un "0" es entrada y las líneas desgarradas donde una "1" es entrada.

Una secuencia codificada real se puede representar como una ruta en este gráfico. Una ruta válida se muestra en rojo como ejemplo.

Este diagrama nos da una idea sobre la descodificación: si una secuencia recibida no se ajusta a este gráfico, entonces se recibió con errores y debemos elegir la correcta (ajustando el gráfico) secuencia. Los verdaderos algoritmos de decodificación explotan esta idea.

Distancia libre y distribución de errores

Curvas de velocidad de bit-error teóricas de QPSK codificado (recursivo y no recursivo, decisión suave), canal de ruido gaisés blanco aditivo. Las curvas son pequeñas distinguidas debido a aproximadamente las mismas distancias y pesos libres.

La distancia libre (d) es la distancia mínima de Hamming entre diferentes secuencias codificadas. La capacidad de corrección (t) de un código convolucional es el número de errores que puede corregir el código. Se puede calcular como

t=⌊d− − 12⌋.{displaystyle No.

Dado que un código convolucional no usa bloques, sino que procesa un flujo de bits continuo, el valor de t se aplica a una cantidad de errores ubicados relativamente cerca uno del otro. Es decir, varios grupos de errores t generalmente se pueden corregir cuando están relativamente separados.

La distancia libre puede interpretarse como la longitud mínima de un "ráfaga" a la salida de un decodificador convolucional. El hecho de que los errores aparezcan como "ráfagas" debe tenerse en cuenta al diseñar un código concatenado con un código convolucional interno. La solución popular para este problema es intercalar datos antes de la codificación convolucional, de modo que el código del bloque externo (generalmente Reed-Solomon) pueda corregir la mayoría de los errores.

Decodificación de códigos convolucionales

Curvas de relación de error de bits para códigos convolutivos con diferentes opciones de modulación digital (QPSK, 8-PSK, 16-QAM, 64-QAM) y Algoritmos LLR. (Exacto y Aproximado) sobre el canal de ruido Gaussiano blanco aditivo.

Existen varios algoritmos para decodificar códigos convolucionales. Para valores relativamente pequeños de k, el algoritmo de Viterbi se usa universalmente ya que proporciona un rendimiento de máxima probabilidad y es altamente paralelizable. Por lo tanto, los decodificadores Viterbi son fáciles de implementar en hardware VLSI y en software en CPU con conjuntos de instrucciones SIMD.

Los códigos de mayor longitud de restricción se decodifican de manera más práctica con cualquiera de varios algoritmos de decodificación secuencial, de los cuales el algoritmo Fano es el más conocido. A diferencia de la decodificación de Viterbi, la decodificación secuencial no es de máxima probabilidad, pero su complejidad aumenta solo ligeramente con la longitud de restricción, lo que permite el uso de códigos fuertes de longitud de restricción larga. Dichos códigos se utilizaron en el programa Pioneer de principios de la década de 1970 para Júpiter y Saturno, pero dieron paso a códigos decodificados por Viterbi más cortos, generalmente concatenados con grandes códigos de corrección de errores Reed-Solomon que aumentan la curva general de tasa de error de bit y producen Tasas de errores residuales no detectados extremadamente bajas.

Tanto Viterbi como los algoritmos de decodificación secuencial arrojan decisiones difíciles: los bits que forman la palabra clave más probable. Se puede agregar una medida de confianza aproximada a cada bit mediante el uso del algoritmo Viterbi de salida suave. Las decisiones flexibles máximas a posteriori (MAP) para cada bit se pueden obtener mediante el uso del algoritmo BCJR.

Códigos convolucionales populares

Registro de cambios para el código converso (7, [171, 133]). Ramas: h1=171o=[1111001]b{displaystyle h^{1}=171_{o}=[1111001]_{b}, h2=133o=[1011011]b{displaystyle h^{2}=133_{o}=[1011011]_{b}. Todas las operaciones de matemáticas deben hacerse por modulo 2.

Curvas de velocidad de bit-error teóricas de QPSK codificado (decisión suave), canal de ruido Gaussiano blanco aditivo. Las longitudes de restricción más largas producen códigos más poderosos, pero la complejidad del algoritmo Viterbi aumenta exponencialmente con longitudes de restricción, limitando estos códigos más poderosos a misiones espaciales profundas donde el rendimiento extra vale fácilmente la mayor complejidad del decodificador.

De hecho, en la industria se utilizan estructuras de códigos convolucionales predefinidos obtenidos durante investigaciones científicas. Esto se relaciona con la posibilidad de seleccionar códigos convolucionales catastróficos (provoca mayor número de errores).

Un código convolucional decodificado por Viterbi especialmente popular, utilizado al menos desde que el programa Voyager tiene una longitud de restricción K de 7 y una tasa r de 1/2.

Mars Pathfinder, Mars Exploration Rover y la sonda Cassini a Saturno utilizan un K de 15 y una tasa de 1/6; este código realiza alrededor de 2 dB mejor que el más simple K=7{displaystyle K=7} código a un costo de 256× en la decodificación de la complejidad (comparado a los códigos de misión Voyager).

El código convolucional con una longitud de restricción de 2 y una tasa de 1/2 se utiliza en GSM como técnica de corrección de errores.

Códigos convolucionales perforados

Códigos conversos con tasas de código 1/2 y 3/4 (y longitud de restricción 7, decisión suave, 4-QAM / QPSK / OQPSK).

El código convolucional con cualquier tasa de código se puede diseñar en función de la selección de polinomios; sin embargo, en la práctica, a menudo se usa un procedimiento de perforación para lograr la tasa de código requerida. La perforación es una técnica utilizada para hacer un código de tarifa m/n a partir de un código de tarifa "básico" código de tasa baja (por ejemplo, 1/n). Se logra borrando algunos bits en la salida del codificador. Los bits se eliminan de acuerdo con una matriz de perforación. Las siguientes matrices de punción son las más utilizadas:

Por ejemplo, si queremos hacer un código con una tasa de 2/3 usando la matriz apropiada de la tabla anterior, debemos tomar una salida de codificador básica y transmitir cada primer bit desde la primera rama y cada bit desde la segunda.. El orden específico de transmisión está definido por el estándar de comunicación respectivo.

Los códigos convolucionales perforados se usan ampliamente en las comunicaciones por satélite, por ejemplo, en los sistemas INTELSAT y la transmisión de video digital.

Los códigos convolucionales perforados también se denominan "perforados".

Códigos turbo: sustitución de códigos convolucionales

Un código turbo con códigos de componentes 13, 15. Los códigos Turbo obtienen su nombre porque el decodificador utiliza la retroalimentación, como un motor turbo. La permutación significa lo mismo que el entrelazamiento. C1 y C2 son códigos convolutivos recurrentes. Los códigos convolutivos recuperativos y no recursivos no son tan diferentes en el rendimiento de BER, sin embargo, el tipo recursivo de se implementa en los códigos convolutivos Turbo debido a mejores propiedades interleatorias.

Los códigos convolucionales simples decodificados por Viterbi ahora están dando paso a códigos turbo, una nueva clase de códigos convolucionales cortos iterados que se acercan mucho a los límites teóricos impuestos por el teorema de Shannon con una complejidad de decodificación mucho menor que el algoritmo de Viterbi en el códigos convolucionales largos que serían necesarios para el mismo rendimiento. La concatenación con un código algebraico externo (p. ej., Reed-Solomon) aborda el problema de los niveles de error inherentes a los diseños de código turbo.