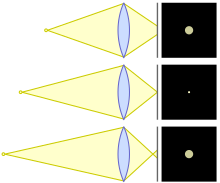
Circulo de confusion

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Región Blurry en óptica

Diagrama mostrando círculos de confusión para fuente de puntos demasiado cerca, en foco, y demasiado lejos

En óptica, un círculo de confusión (CoC) es un punto óptico causado por un cono de rayos de luz de una lente que no llega a un enfoque perfecto al obtener imágenes de una fuente puntual. También se conoce como disco de confusión, círculo de indistinción, círculo borroso o punto borroso.

En fotografía, el círculo de confusión se usa para determinar la profundidad de campo, la parte de una imagen que es aceptablemente nítida. Un valor estándar de CoC a menudo se asocia con cada formato de imagen, pero el valor más apropiado depende de la agudeza visual, las condiciones de visualización y la cantidad de ampliación. Los usos en contexto incluyen círculo de confusión máximo permitido, límite de diámetro del círculo de confusión y el criterio del círculo de confusión.

Los lentes reales no enfocan todos los rayos a la perfección, por lo que incluso en el mejor enfoque, un punto se refleja como un punto en lugar de como un punto. La mancha más pequeña que puede producir una lente se suele denominar círculo de menor confusión.

Dos usos

Es necesario distinguir dos usos importantes de este término y concepto:

En una lente perfecta $L$ , todos los rayos pasan a través de un punto focal $F$ . Sin embargo a otras distancias de la lente los rayos forman un círculo.
Para describir el punto de desdibujo más grande que es indistinguible desde un punto. Un objetivo puede enfocar precisamente objetos a sólo una distancia; los objetos a otras distancias son defocused. Los puntos de objeto desfocados se consideran como manchas borrosas en lugar de puntos; cuanto mayor es la distancia que un objeto es del plano de enfoque, mayor es el tamaño del punto de desenfoque. Tal punto borroso tiene la misma forma que la abertura de la lente, pero para la simplicidad, se trata generalmente como si fuera circular. En la práctica, los objetos a distancias considerablemente diferentes de la cámara todavía pueden aparecer afilados; la gama de distancias de objetos sobre las cuales los objetos aparecen afilados es la profundidad del campo (DoF). El criterio común para la "agudez aceptable" en la imagen final (por ejemplo, impresión, pantalla de proyección o visualización electrónica) es que el punto de desdibujado sea indistinguible desde un punto.
En una lente imperfecta $L$ , no todos los rayos pasan a través de un punto focal. El círculo más pequeño que pasan a través $C$ se llama el círculo de menos confusión.
Para describir el punto borroso alcanzado por una lente, en su mejor enfoque o más generalmente. Reconociendo que los lentes reales no enfocan todos los rayos perfectamente bajo las mejores condiciones, el término círculo de menos confusión a menudo se utiliza para el punto de desenfoque más pequeño que un lente puede hacer, por ejemplo, eligiendo una mejor posición de enfoque que hace un buen compromiso entre las longitudes focales variables de diferentes zonas de lente debido a aberraciones esféricas u otras. El término círculo de confusión se aplica más generalmente, al tamaño del punto fuera de foco al que una lente imprime un punto objeto. Los efectos de la disfracción de la óptica de onda y la abertura finita de una lente determinan el círculo de menor confusión; el uso más general de "circo de confusión" para puntos fuera de foco puede ser calculado puramente en términos de óptica de rayos (geométrica).

En la óptica de rayos idealizada, donde se supone que los rayos convergen en un punto cuando están perfectamente enfocados, la forma de un punto borroso de desenfoque de una lente con una apertura circular es un círculo de luz de bordes duros. Un punto borroso más general tiene bordes suaves debido a la difracción y las aberraciones, y puede no ser circular debido a la forma de la apertura. Por lo tanto, el concepto de diámetro debe definirse cuidadosamente para que tenga sentido. Las definiciones adecuadas suelen utilizar el concepto de energía rodeada, la fracción de la energía óptica total del punto que se encuentra dentro del diámetro especificado. Los valores de la fracción (p. ej., 80 %, 90 %) varían según la aplicación.

Límite del diámetro del círculo de confusión en fotografía

En fotografía, el límite del diámetro del círculo de confusión (límite de CoC o criterio de CoC) a menudo se define como el punto borroso más grande que aún será percibido por el ojo humano. como un punto, cuando se ve en una imagen final desde una distancia de visualización estándar. El límite de CoC se puede especificar en una imagen final (por ejemplo, una impresión) o en la imagen original (en película o sensor de imagen).

Con esta definición, el límite de CoC en la imagen original (la imagen en la película o el sensor electrónico) se puede establecer en función de varios factores:

Agudeza visual. Para la mayoría de las personas, la distancia de vista más cómoda más cercana, llamó la cerca de la distancia para una visión distinta, es aproximadamente 25 cm. A esta distancia, una persona con buena visión puede distinguir generalmente una resolución de imagen de 5 pares de línea por milímetro (lp/mm), equivalente a un CoC de 0,2 mm en la imagen final.
Ver las condiciones. Si la imagen final es vista aproximadamente a 25 cm, es apropiado un CoC de imagen final de 0.2 mm. Una distancia de visualización cómoda es también una a la que el ángulo de vista es de aproximadamente 60°; a una distancia de 25 cm, esto corresponde a unos 30 cm, aproximadamente la diagonal de una imagen de 8 pulgadas × 10 pulgadas (para comparación, papel A4 es 8.3 en × 11.7 en, 210 mm × 297 mm; papel de carta estadounidense es 8.5 en × 11 en, 216 mm × 279 mm). A menudo puede ser razonable suponer que, para la visualización de imágenes completas, una imagen final mayor de 8 en × 10 en se verá a una distancia correspondientemente mayor de 25 cm, y para la cual un CoC más grande puede ser aceptable; el CoC de imagen original es entonces el mismo que el que determina del tamaño de imagen final estándar y la distancia de visualización. Pero si la imagen final más grande será vista a la distancia normal de 25 cm, se necesitará un CoC de imagen original más pequeño para proporcionar una agudeza aceptable.
Ampliación de la imagen original a la imagen final. Si no hay ampliación (por ejemplo, una impresión de contacto de una imagen original de 8×10), el CoC para la imagen original es el mismo que en la imagen final. Pero si, por ejemplo, la dimensión larga de una imagen original de 35 mm se agranda a 25 cm (10 pulgadas), el factor de ampliación es aproximadamente 7, y el CoC para la imagen original es de 0.2 mm / 7, o 0.029 mm.

Los valores comunes para el límite de CoC pueden no ser aplicables si las condiciones de reproducción o visualización difieren significativamente de las supuestas para determinar esos valores. Si la imagen original se ampliará más o se verá a una distancia más cercana, se requerirá un CoC más pequeño. Los tres factores anteriores se acomodan con esta fórmula:

CoC (en mm) = (Vista distancia (en cm) / 25 cm) / (Resolución de imagen final deseada en lp/mm para una distancia de visualización de 25 cm) / ampliación

Por ejemplo, para admitir una resolución de imagen final equivalente a 5 lp/mm para una distancia de visualización de 25 cm cuando la distancia de visualización prevista es de 50 cm y la ampliación prevista es de 8:

CoC = (50 / 25) / 5 / 8 = 0,05 mm

Dado que el tamaño de la imagen final generalmente no se conoce al momento de tomar una fotografía, es común asumir un tamaño estándar como 25 cm de ancho, junto con un CoC de imagen final convencional de 0,2 mm, que es 1 /1250 del ancho de la imagen. Las convenciones en términos de la medida diagonal también se usan comúnmente. El DoF calculado utilizando estas convenciones deberá ajustarse si la imagen original se recorta antes de ampliarla al tamaño final de la imagen, o si se modifican las suposiciones de visualización y tamaño.

Para el formato de fotograma completo de 35 mm (24 mm × 36 mm, 43 mm de diagonal), un límite de CoC muy utilizado es $d$ /1500, o 0,029 mm para formato de fotograma completo de 35 mm, lo que corresponde a la resolución de 5 líneas por milímetro en una impresión de 30 cm de diagonal. Los valores de 0,030 mm y 0,033 mm también son comunes para el formato de fotograma completo de 35 mm.

También se han utilizado criterios que relacionan CoC con la distancia focal de la lente. Kodak recomendó 2 minutos de arco (el criterio de Snellen de 30 ciclos/grado para una visión normal) para una visualización crítica, lo que genera un CoC de aproximadamente $f$ /1720, donde $f$ es la distancia focal de la lente. Para una lente de 50 mm en formato de fotograma completo de 35 mm, el CoC correspondiente es 0,0291 mm. Este criterio evidentemente asumía que una imagen final se vería a la distancia de perspectiva correcta (es decir, el ángulo de visión sería el mismo que el de la imagen original):

Ver distancia = longitud focal de tomar lente × ampliación

Sin embargo, las imágenes rara vez se ven en el llamado 'correcto' distancia; el espectador por lo general no conoce la distancia focal de la lente de toma, y el "correcto" la distancia puede ser incómodamente corta o larga. En consecuencia, los criterios basados en la distancia focal del objetivo han dado paso generalmente a criterios (como $d$ /1500) relacionados con el formato de la cámara.

Si una imagen se ve en un medio de visualización de baja resolución, como un monitor de computadora, la detección de la borrosidad estará limitada por el medio de visualización y no por la visión humana. Por ejemplo, la borrosidad óptica será más difícil de detectar en una imagen de 8 x 10 pulgadas que se muestra en un monitor de computadora que en una impresión de 8 x 10 de la misma imagen original vista a la misma distancia. Si la imagen se va a ver solo en un dispositivo de baja resolución, puede ser apropiado un CoC más grande; sin embargo, si la imagen también se puede ver en un medio de alta resolución, como una impresión, prevalecerán los criterios discutidos anteriormente.

Las fórmulas de profundidad de campo derivadas de la óptica geométrica implican que se puede lograr cualquier DoF arbitrario mediante el uso de un CoC suficientemente pequeño. Sin embargo, debido a la difracción, esto no es del todo cierto. El uso de un CoC más pequeño requiere aumentar el número f de la lente para lograr el mismo DoF, y si la lente se detiene lo suficiente, la reducción en el desenfoque del desenfoque se compensa con el aumento del desenfoque de la difracción. Consulte el artículo Profundidad de campo para obtener una discusión más detallada.

Límite del diámetro del círculo de confusión basado en d/1500

Diámetro CoC basado en $d$ /1500 para varios formatos de imagen
Formato de imagen	Clase de formato	Tamaño de la estructura	CoC
1" sensor (Nikon 1, Sony RX10, Sony RX100)	Formato pequeño	8,8 mm × 13,2 mm	0,011 mm
Sistema de cuatro tercios		13.5 mm × 18 mm	0,015 mm
APS-C		15.0 mm × 22.5 mm	0,018 mm
APS-C Canon		14.8 mm × 22.2 mm	0,018 mm
APS-C Nikon/Pentax/Sony		15,7 mm × 23,6 mm	0,019 mm
APS-H Canon		19.0 mm × 28,7 mm	0,023 mm
35 mm		24 mm × 36 mm	0,029 mm
645 (6×4.5)	Formato medio	56 mm × 42 mm	0,047 mm
6×6		56 mm × 56 mm	0,053 mm
6×7		56 mm × 69 mm	0,059 mm
6×9		56 mm × 84 mm	0,067 mm
6×12		56 mm × 112 mm	0,083 mm
6×17		56 mm × 168 mm	0,12 mm
4×5	Formato grande	102 mm × 127 mm	0,11 mm
5×7		127 mm × 178 mm	0,15 mm
8×10		203 mm × 254 mm	0.22 mm

Ajuste del diámetro del círculo de confusión para la escala DoF de una lente

El número f determinado a partir de una escala DoF de lente se puede ajustar para reflejar un CoC diferente del que se basa en la escala DoF. En el artículo Profundidad de campo se muestra que

{displaystyle mathrm {DoF} ={frac {2Ncleft(m+1right)}{m^{2}-left({frac {Nc}{f}}right)^{2}}},,}

donde $N$ es el número f de la lente, $c$ es el CoC, $m$ es la ampliación y $f$ es la distancia focal de la lente. Debido a que el número f y CoC ocurren solo como el producto $Nc$ , un aumento en uno es equivalente a una disminución correspondiente en el otro. Por ejemplo, si se sabe que la escala DoF de una lente se basa en un CoC de 0,035 mm y las condiciones reales requieren un CoC de 0,025 mm, el CoC debe reducirse en un factor de 0,035 / 0,025 = 1,4; esto se puede lograr aumentando el número f determinado a partir de la escala DoF por el mismo factor, o alrededor de 1 punto, de modo que la lente simplemente se puede cerrar 1 punto por debajo del valor indicado en la escala.

Por lo general, se puede usar el mismo enfoque con una calculadora de profundidad de campo en una cámara de visualización.

Determinación del diámetro de un círculo de confusión a partir del campo del objeto

Esquema de lentes y rayos para calcular el círculo del diámetro de la confusión

c

para un sujeto fuera de foco a distancia

S 2

cuando la cámara se centra en

S 1

. El círculo de borrón auxiliar

C

en el plano objeto (línea bajada) facilita el cálculo.

Un cálculo temprano del diámetro de CoC ("indistinctness") por "T.H." en 1866.

Para calcular el diámetro del círculo de confusión en el plano de la imagen para un sujeto desenfocado, un método consiste en calcular primero el diámetro del círculo de desenfoque en una imagen virtual en el plano del objeto, lo que se hace de forma sencilla utilizando triángulos similares, y luego multiplicar por la ampliación del sistema, que se calcula con la ayuda de la ecuación de la lente.

El círculo de desenfoque, de diámetro $C$ , en el plano del objeto enfocado a la distancia $S 1$ , es una imagen virtual desenfocada del objeto a la distancia $S 2$ como se muestra en el diagrama. Depende únicamente de estas distancias y del diámetro de apertura $A$ , a través de triángulos similares, independientemente de la distancia focal de la lente:

{displaystyle C=A{|S_{2}-S_{1}| over S_{2}},.}

El círculo de confusión en el plano de la imagen se obtiene multiplicando por el aumento $m$ :

{displaystyle c=Cm,,}

donde el aumento $m$ viene dado por la relación de las distancias de enfoque:

{displaystyle m={f_{1} over S_{1}},.}

Usando la ecuación de la lente podemos resolver la variable auxiliar $f 1$ :

{displaystyle {1 over f}={1 over f_{1}}+{1 over S_{1}},,}

que produce

{displaystyle f_{1}={fS_{1} over S_{1}-f},,}

y exprese la ampliación en términos de distancia enfocada y distancia focal:

{displaystyle m={f over S_{1}-f},,}

que da el resultado final:

{displaystyle c=A{|S_{2}-S_{1}| over S_{2}}{f over S_{1}-f},.}

Esto se puede expresar opcionalmente en términos del número f $N = f/A$ como:

{displaystyle c={|S_{2}-S_{1}| over S_{2}}{f^{2} over N(S_{1}-f)},.}

Esta fórmula es exacta para una lente delgada paraxial simple o una lente simétrica, en la que la pupila de entrada y la pupila de salida tienen un diámetro $A$ . Los diseños de lentes más complejos con un aumento de pupila no unitario necesitarán un análisis más complejo, como se aborda en la profundidad de campo.

Más generalmente, este enfoque conduce a un resultado paraxial exacto para todos los sistemas ópticos si $A$ es el diámetro de la pupila de entrada, el las distancias del sujeto se miden desde la pupila de entrada y se conoce el aumento:

{displaystyle c=Am{|S_{2}-S_{1}| over S_{2}},.}

Si la distancia de enfoque o la distancia del sujeto desenfocado es infinita, las ecuaciones se pueden evaluar en el límite. Para una distancia de enfoque infinita:

{displaystyle c={fA over S_{2}}={f^{2} over NS_{2}},.}

Y para el círculo de desenfoque de un objeto en el infinito cuando la distancia de enfoque es finita:

{displaystyle c={fA over S_{1}-f}={f^{2} over N(S_{1}-f)},.}

Si el valor de $c$ se fija como un límite de diámetro del círculo de confusión, cualquiera de estos se puede resolver para la distancia del sujeto a obtener la distancia hiperfocal, con resultados aproximadamente equivalentes.

Historia

Henry Coddington 1829

Antes de que se aplicara a la fotografía, el concepto de círculo de confusión se aplicó a instrumentos ópticos como los telescopios. Coddington (1829, p. 54) cuantifica tanto un círculo de mínima confusión como un círculo de mínima confusión para una superficie reflectante esférica.

Esto podemos considerar como el enfoque más cercano a un enfoque simple, y llamar el círculo de menos confusión.

Sociedad para la Difusión del Conocimiento Útil 1832

La Society for the Diffusion of Useful Knowledge (1832, p. 11) lo aplicó a las aberraciones de tercer orden:

Esta aberración esférica produce una indistintitud de la visión, difundiendo cada punto matemático del objeto en un pequeño punto en su imagen; que manchas, al mezclarse entre sí, confunden todo. El diámetro de este círculo de confusión, en el foco de los rayos centrales F, sobre el cual se extiende cada punto, será L K (fig. 17.); y cuando la abertura del reflector es moderada equivale al cubo de la abertura, dividida por la plaza del radio (...): este círculo se llama la aberración de la latitud.

T.H. 1866

Cálculos del círculo de confusión: un precursor temprano de los cálculos de profundidad de campo es el cálculo de TH (1866, p. 138) del diámetro del círculo de confusión desde la distancia del sujeto, para una lente enfocada al infinito; este artículo fue señalado por von Rohr (1899). La fórmula que se le ocurre para lo que él llama "la indistinción" es equivalente, en términos modernos, a

{displaystyle c={fA over S}}

para distancia focal $f$ , diámetro de apertura $A$ y la distancia del sujeto $S$ . Pero no invierte esto para encontrar la $S$ correspondiente a un $c$ criterio (es decir, no resuelve la distancia hiperfocal), ni considera enfocar a ninguna otra distancia que no sea el infinito.

Finalmente observa que "los lentes de enfoque largo generalmente tienen una apertura más grande que los cortos y por esta razón tienen menos profundidad de enfoque" [énfasis suyo en cursiva].

Dallmeyer y Abney

Dallmeyer (1892, p. 24), en una reedición ampliada del folleto de 1874 de su padre John Henry Dallmeyer (Dallmeyer 1874) Sobre la elección y el uso de lentes fotográficos (en material que no está en la edición de 1874 y parece haber sido agregado de un artículo de J.H.D. 'Sobre el uso de diafragmas o topes' de fecha desconocida), dice:

Así cada punto en un objeto fuera de foco está representado en la imagen por un disco, o círculo de confusión, cuyo tamaño es proporcional a la abertura en relación con el enfoque de la lente empleada. Si un punto en el objeto es 1/100 de pulgada fuera de foco, estará representado por un círculo de medición de confusión pero 1/100 parte de la abertura de la lente.

Esta última afirmación es claramente incorrecta o errónea, ya que se desvía por un factor de distancia focal (longitud focal). Él continúa:

y cuando los círculos de confusión son suficientemente pequeños el ojo no los ve como tal; entonces se ven sólo como puntos, y la imagen aparece aguda. A la distancia ordinaria de la visión, de doce a quince pulgadas, círculos de confusión se ven como puntos, si el ángulo subtended por ellos no excede un minuto de arco, o aproximadamente, si no exceden el 1/100 de un pulgada de diámetro.

Numéricamente, 1/100 pulgada a 12–15 pulgadas está más cerca de dos minutos de arco. Esta elección de límite de CoC sigue siendo (para una letra grande) la más utilizada incluso hoy en día. Abney (1881, pp. 207-08) adopta un enfoque similar basado en una agudeza visual de un minuto de arco y elige un círculo de confusión de 0,025 cm para ver a 40-50 cm, esencialmente haciendo el mismo factor de dos errores en unidades métricas. No está claro si Abney o Dallmeyer establecieron antes el estándar CoC.

Muro 1889

El límite de CoC común de 1/100 pulgadas se ha aplicado a desenfoques que no sean desenfoque. Por ejemplo, Wall (1889, p. 92) dice:

Para encontrar lo rápido que un obturador debe actuar para tomar un objeto en movimiento que puede haber un círculo de confusión menos de 1/100 pulg. en diámetro, dividir la distancia del objeto por 100 veces el foco de la lente, y dividir la rapidez del movimiento del objeto en pulgadas por segundo por los resultados, cuando usted tiene la duración más larga de la exposición en fracción de segundo.

Contenido relacionado

Más resultados...